Дополнение к теории Бишопа-Хилла пластического формоизменения монокристалла

Многие современные работы, посвященные теоретическому анализу и моделированию пластического поведения металлических поликристаллов, в значительной степени опираются на классический анализ пластического формоизменения монокристалла, выполненный GJ. Taylor [1], J.F.W. Bishop и R. Hill [2-3] и J.F.W. Bishop [4]. В этих работах рассматривались ГЦК-монокристаллы с жестко-пластическими свойствами, деформирующиеся путем кристаллографического скольжения. Закон Шмида, установленный в опытах на единичное скольжение монокристалла, авторы [2] обобщили на случай произвольного деформированного состояния и с помощью полученного критерия текучести (называемого критерием Бишопа-Хилла) и закона течения в терминах связанных с системами скольжения переменных обосновали локальный принцип максимума и принцип минимума суммарного сдвига Тейлора [1]. Указанный принцип максимума был использован в работе [3] для нахождения тензора напряжений. соответствующего заданному тензору приращений пластических деформаций, а принцип минимума. -— в работе [1] для нахождения набора приращений сдвигов, реализующих заданный тензор приращения деформаций.

Более поздняя публикация R. Hill [5], однако, позволяет дополнить этот анализ. Выбирая обобщение закона Шмида, на. произвольное деформированное состояние с использованием любой достаточно точно согласующейся с экспериментом нормы, мы получим соответствующий принцип минимума, сдвига и следующие из него законы пластического течения, с помощью которых представляется возможным построить определяющие соотношения. В настоящей работе подробно исследуется семейство степенных норм; классический анализ в рамках такого предположения будет являться предельным случаем, т. е. справедливым при стремлении показателя степени к бесконечности.

Экстремальные принципы1

Ограничимся случаем малых градиентов перемещений, в рамках которого пластическое формоизменение среды может быть описано девиатором 6Р тензора скорости деформаций Эйлера. В таком случае функционалами удельной мощности пластического формоизменения на элементах пространства симметричных девиаторов ер являются девиаторы s тензоров напряжений Коши (см. приложение). Тензор бр реализуют скорости сдвигов ^к по системам скольжения ГЦК-монокристалла

₆р = -₍^кт_к,                                                                    (1)

где к, = 1...12 (здесь и далее в работе используется соглашение о суммировании по “немым” индексам), т_к - симметризованная диада, состоящая из векторов, характеризующих к-ю систему скольжения, т_к = ^(n_k®b_k-Vb_k®n_k'), где п_к и Ь_к - единичные векторы соответственно нормали к плоскости скольжения и направления скольжения, а “®” обозначает диадное произведение: величины ^^к в (1) могут быть любого знака. Набор т_к для ГЦК-решетки содержит базис пространства симметричных девиаторов Tig, то есть

£(т_г, ,.,т₁₂) =                                                             (2)

где С^ есть символ линейной оболочки. Движущими силами кристаллографического скольжения являются приведенные напряжения тк = smk                                                                (3)

(свободные индексы к здесь и далее в работе принимают значения 1...12). Поскольку заданный тензор 6^Р в силу (Г) может порождаться различными наборами скоростей сдвигов у^, рассмотрим пространство Л12 векторов 7 с компонентами 7^' в некотором базисе е_к Е Ли- Поскольку в силу (1) и (3) se^p = т^^ можно рассмотреть сопряженное пространство Л^₂ векторов т с компонентами т_к в сопряженном базисе е^к Е Ли- Заметим, однако, что интересующие нас векторы т согласно (3) образуют пятимерное подпространствоЛз С Л^- Далее, элементы из Л₅, порожденные некоторым тензором s, будем обозначать т_в (не путать с компонентами г!).

Рекомендуется предварительно ознакомиться с приложением.

В пространстве Л^ определим выпуклую однородную первой степени функцию р(т), равноправную относительно координат аргумента, с помощью которой может быть записан критерий текучести монокристалла

Ф^т.ф = Гсг, где гст - некоторый критический параметр размерности напряжения фф^ф как функцию s будем обозначать ф\з^ = Ф(т5), тогда критерий (4) может быть записан в форме ф'(,8) = гст (4')).

Пусть задан е^р, параллельный внешней нормали к поверхности текучести (4') в Л.5 в точке s. Вектор 7 назовем геометрически возможным, если он удовлетворяет ограничению (1) при заданном 6^Р. Физически возможным назовем вектор 7, нормальный поверхности текучести (4) (в Лу) ^в точке т₅. Задача нахождения геометрически и физически возможного 7 эквивалентна задаче нахождения продолжения е^р на все пространство Лу с сохранением нормы, поскольку 7 есть продолжение е^р. а сформулированное условие нормальности эквивалентно условию сохранения нормы е^р. Норма €^р находится в терминах Л5 согласно определению (А1) приложения: обозначим ее фф€^рф

Имеет место следующий принцип минимума сдвига: геометрически и физически, возможный находится как решение задачи фф*ф mm, ер = ^kmk. (о)

Действительно, условие (6)2 есть условие геометрической возможности 7, а согласно неравенству (А2) приложения

ф^т^ ффв) V

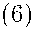
и условие (5)i обеспечивает физическую возможность 7. Очевидно, что по определению физически и геометрически возможного 7 связь 7 и т, может быть записана в виде следующего принципа максимума:

177 -* max, ^(т$) = гсг,                                               (7)

из которого в силу (3) следует так называемый локальный принцип максимума sep max.           " rCT.                                                     (8)

Заметим, однако, что общность приведенных здесь результатов ограничена случаем изотропного упрочнения, что связано с ограничениями на функцию ф^тУ

Полагая 3(т) = тах|тД, как авторы [1-4], из (7) следует принятый в этих работах закон пластического течения. Очевидно, что этот закон удовлетворяет локальному принципу максимума (8) и принципу минимума сдвига. (5) (с нормой б*(7) = У, ф-ф. являющейся двойственной к р(т)); последний был сформулирован в работе [1] ^k '

и доказан в работе [2]. Кроме того, на основе приведенной здесь теории может быть элементарно доказана рассмотренная в работе [4] теорема существования.

Степенной критерий текучести

Рассмотрим в качестве функций текучести семейство степенных норм

^(г) = (ХЫ’)^’   2 < 9 < ос.                                  (9)

к

Потребуем, чтобы критерий (4) сводился к критерию Шмида, то есть предсказывал текучесть при единичном скольжении s = т_сгШ/, где т_ст - критическое сдвиговое напряжение, а индекс “Z” фиксирован и может быть любым. Тогда условие (4) принимает вид

^(s) = ТстфЧт^,                                                     (10)

причем, очевидно, что ф\т^ не зависит от I, а зависит от д; обозначим ф'^тп^ = v(q\

Может быть показано, что уравнение (10) задает ограниченную, гладкую и строго выпуклую поверхность в пространстве напряжений s, причем ограниченность обеспечивается условием (2). Также можно доказать, что поверхности (10) при q — ^оо стремятся к поверхности многогранника Бишопа-Хилла, находясь внутри него.

Наложенное на г_ст требование обеспечивает наличие 24 общих точек поверхности (10) при любом q и многогранника Бишопа-Хилла, соответствующих единичному скольжению. В случае деформирования, отличного от единичного скольжения, текучесть согласно (10) может наступить, когда ни на одной системе скольжения не выполняется закон Шмида, однако в этом случае он выполняется приближенно. Точ ность приближения может быть выбрана сколь угодно высокой увеличением q. Отличием построенного критерия от формулировки Бишопа-Хилла является то, что он учитывает вклад всех приведенных напряжений в условие текучести.

Построенному критерию может быть придан энергетический смысл. С этой целью рассмотрим класс металлов с сильно нелинейной кривой обратимого деформирования, предшествующего состоянию текучести, нелинейность которой вызвана дислокационным механизмом. Данный механизм представляет собой упругое смещение локальных дефектов решетки, поджатых к барьерам. Нелинейность зависимости напряжений от деформаций в такой модели объясняется стохастическим распределением упругих свойств дислокаций, вызванным хаотической ориентацией дислокаций в плоскостях залегания, а также наличием в кристалле спектра барьеров с различными упругими характеристиками.

В предположении, что поджатые дислокации залегают в плоскостях скольжения, в качестве потенциала таких (“обратимых") деформаций выбирается U(s), так что

6r=W(s),                                           (Ш где ег есть девиатор тензора обратимых деформаций, а V есть градиент с частными производными по компонентам s. Выберем функцию U^s) в виде

=                                              (12)

где е - параметр истории пластического формоизменения, как самый простой случай, качественно согласующийся с экспериментальными данными. Тогда, рассчитывая энергию обратимых деформаций W(s), получим, что в состоянии текучести согласно (10) ИДз) = е, то есть параметр е имеет смысл предельного значения энергии. Критерий (10), следовательно, предсказывает начало текучести в момент, когда энергия обратимых деформаций достигает предельного значения. В пределе при g —> ос рассматриваемый закон гиперупругости сводится к классическому закону течения жестко-пластической среды.

Определяющие соотношения

Получим на основе сформулированного критерия и экстремальных принципов ряд определяющих соотношений, могущих быть использованными для вывода, определяющих соотношений поликристалла, а также для непосредственного использования в расчетах монокристаллических изделий.

Примем гипотезу е = ер,

где е символизирует девиатор скоростей полных деформаций, и предположим также, что среда не упрочняется. Для данной жестко-идеально-пластической среды с помощью принципа (7) и соотношений (10) и (АЗ) получим законы

A sm, ^(q)⁴^^{1 Т}ст

sm, q 2

^'(s) = r_CT

с помощью которых покоординатным умножением на соответствующие диадики т^ и суммированием по к получаем закон в терминах тензоров сиз или, выделив тензор А четвертого ранга (зависящий от з),в виде

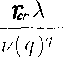
As,

Ф\8^ = ТС1..

Заметим, что законы (14) следуют также из принципа минимума (5), поскольку геометрически и физически возможный 7 существует, а физически возможный 7 в силу строгой выпуклости >(•) единственный и есть (14). Также отметим, что (15) непосредственно следует из локального принципа максимума. С помощью законов (14) можно выяснить роль параметра, q в тензоре пластических свойств А. Рассматривая напряженное состояние s = r„mi (I фиксирован), вызывающее (’циничное скольжение, из (14) можно найти модули относительных сдвигов фА| = гД гЛ 1 |yfc| = \mimk\q"\

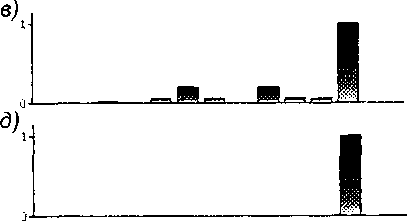
Рис. 1: Относительное распределение сдвига по всем системам скольжения при единичном скольжении согласно (14): a) q = 2, б) g — 3, в) q = 5, г) q = 9, д) q—*oc.

б^

Системы скольжения

Распределение |7'*| по всем системам скольжения монокристалла для q = 2,3,5 и 9 показано на рис.1, а-г. На рис.1, д для сравнения показан случай единичного скольжения, соответствующего течению на грани многогранника Бишопа-Хилла согласно закону Шмида. Параметр q управляет относительным распределением сдвигов; при увеличении q уменьшается количество фактически действующих систем скольжения, а деформация концентрируется по системам с наибольшими приведенными напряжениями. В пределе при g —> оо активны только системы скольжения с максимальным приведенным напряжением.

Сделаем обобщение модели на случай изотропного упрочнения. Примем закон течения в форме е = д W'(s) ^'(s^s, ф'(8) = гсг, d(

где д - функция упрочнения. Из последнего условия системы (18) получим

^ф\з^8 = v^tct.(19)

Умножая (18)1 скалярно на s, используя критерий (18)з и равенство (19), получим se = д гст Цд) тст.(20)

Согласно (1) и (3) 8€ = t_s7; поскольку т₈ соответствует 7 и доставляет равенство в (А1), то (20) приводится к виду

= 9 v(q) т„.(21)

Считая известным закон упрочнения т_ст(ф(Г^, где Г есть вектор сдвигов (не скоростей сдвигов !), получим (1т_ст = т'_ст dij?(r) (здесь символ “/” обозначает производную).

При условии пропорционального деформирования d^(F) = ф^Г) и из (21) может быть найден вид функции упрочнения

9 = пЛ

■Заметим, что аналогичный закон был сформулирован в работе [2] для рассматривавшегося там потенциала.

В заключение, не приводя формулировок, заметим, что рассматривая упруго-иде- ально-пластическую среду, где в качестве упругих приняты обратимые деформации, и строя типовым способом определяющие соотношения, получим модель, обладающую рядом достоинств. Во-первых, критерий в рамках такой модели будет иметь естественный энергетический смысл, а во-вторых, при достижении текучести будет отсутствовать излом направления деформирования, что достигнуто в рамках настоящей работы выборохохвицотенциалей обратимых деформаций, подобных поверхности текучести. \ (