Достаточный критерий устойчивости и компактности плоских ионных пучков в трехмерных электрических и магнитных полях с плоскостью симметрии
Автор: Бердников Александр Сергеевич, Краснова Н.К.
Журнал: Научное приборостроение @nauchnoe-priborostroenie
Рубрика: Математические методы и моделирование в приборостроении
Статья в выпуске: 2 т.25, 2015 года.
Бесплатный доступ
Рассматривается проблема устойчивости пучков заряженных частиц, которая возникает при отклонении движения частиц от плоскости симметрии z = 0 электрического и/или магнитного поля. Для электрических полей показано, что если для электростатического потенциала U(x, y), заданного в плоскости симметрии z = 0, выполнено условие Uxx + Uyy
Электронная оптика, компактные пучки заряженных частиц, устойчивость движения, синтез оптимальных электронно-оптических систем
Короткий адрес: https://sciup.org/14264979
IDR: 14264979 | УДК: 681.787.7
Текст научной статьи Достаточный критерий устойчивости и компактности плоских ионных пучков в трехмерных электрических и магнитных полях с плоскостью симметрии
Рассматривается проблема устойчивости пучков заряженных частиц, которая возникает при отклонении движения частиц от плоскости симметрии z = 0 электрического и/или магнитного поля. Для электрических полей показано, что если для электростатического потенциала U ( x , y ), заданного в плоскости симметрии z = 0, выполнено условие U xx + U yy < – ε 2< 0, то это будет достаточным условием, чтобы при малом отклонении положительно заряженных частиц от плоскости симметрии z = 0 пучок, двигающийся в данном электрическом поле, оставался в ограниченной окрестности плоскости симметрии. Дополнительно возможно построить конструктивные оценки, насколько далеко от плоскости симметрии может удаляться траектория при заданном возмущении начальных условий. Указанный достаточный критерий устойчивости и компактности пучков может быть обобщен для магнитных полей с плоскостью симметрии и для совмещенных электростатических и магнитостатических полей с общей плоскостью симметрии.
Кл. сл. : электронная оптика, компактные пучки заряженных частиц, устойчивость движения, синтез оптимальных электронно-оптических систем
ПОСТАНОВКА ЗАДАЧИ
Существуют эффективные алгоритмы синтеза электростатических и магнитостатических полей, обеспечивающих желаемое двумерное движение заряженных частиц в плоскости симметрии электрического поля, магнитного поля или совмещенных электрических и магнитных полей с общей плоскостью симметрии [1–10]. Однако, после того как обеспечено желаемое движение пучка заряженных частиц в плоскости симметрии, возникает важный вопрос: что происходит с траекториями заряженных частиц при их незначительном отклонении от плоскости симметрии? Насколько поведение реального пучка с конечной толщиной соответствует идеализированному поведению бесконечно тонкого пучка, которое было рассчитано теоретически?
Рассмотрим типовую схему использования метода обратной задачи по созданию электронно-или ионно-оптической системы, решающей ту или иную практическую проблему. Имеется априорно заданное желаемое поведение пучка заряженных частиц, требуется сконструировать электрические и магнитные поля (а также порождающие их электроды, магниты и катушки с током), которые обеспечат именно такое движение заряженных частиц. При использовании методов [1–10] безупречное поведение бесконечно тонкого пучка гарантируется самой процедурой синтеза распреде- ления электрического и/или магнитного полей для плоскости симметрии z = 0. По известным данным о синтезированных в плоскости симметрии электрическом и магнитном полях и с учетом требования симметричности поля можно однозначным образом восстановить поле во всем пространстве или по крайней мере в некоторой окрестности плоскости симметрии. Как результат на выходе можно получить конфигурацию электродов, полюсных наконечников и катушек с током, нужных для создания искомого трехмерного поля.
Однако устойчивость пучка к малым отклонениям от плоскости симметрии будет реализовываться далеко не для всех синтезированных симметричных электромагнитных полей. Задачей данной работы является получение достаточного критерия устойчивости и компактности электронных и ионных пучков в трехмерных электрических и магнитных полях с плоскостью симметрии. Этот критерий удается сформулировать в таком виде, что для его проверки достаточно знания о распределении электрического и магнитного полей в плоскости симметрии (а также знания базовых траекторий в плоскости симметрии); восстанавливать электрическое и магнитное поля во всем трехмерном пространстве для проверки устойчивости при выходе за пределы плоскости симметрии не требуется. В качестве примера полезность рассматриваемого критерия будет продемонстрирована на частном случае анализа работы двух отклоняющих систем в виде электростатических зеркал, которые характеризуются электрическими потенциалами, однородными по Эйлеру с нулевым показателем однородности (теория таких отклоняющих систем подробно излагается в [3, 10–12]).
УСТОЙЧИВОСТЬ И КОМПАКТНОСТЬ ПЛОСКОГО ПУЧКА В ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЯХ С ПЛОСКОСТЬЮ СИММЕТРИИ
Ограничимся для начала частным случаем движения заряженных частиц в чисто электростатическом поле с плоскостью симметрии. Для того чтобы гарантированно обеспечивать устойчивость (локализацию в окрестности плоскости симметрии) пучка заряженных частиц при малых отклонениях от плоскости симметрии z = 0, полезна следующая теорема.
Теорема. Имеется трехмерный электрический потенциал U ( x , y , z ) с плоскостью симметрии z = 0: U ( x , y , - z ) = U ( x , y , + z ) и рассматривается движение заряженных частиц в окрестности плоскости z = 0. Чтобы при малых отклонениях начальных условий заряженной частицы от плоскости OXY движение оставалось глобально локализованным в окрестности плоскости z = 0, достаточно выполнения на множестве точек плоскости OXY , заполненного лежащими в плоскости симметрии траекториями, условия 9 2 U /д z 2 > s 2 > 0 в случае положительно заряженных частиц и условия 9 2 U /д z 2 < — s 2 < 0 в случае отрицательно заряженных частиц.
Из этой теоремы, доказательство которой будет приведено далее, имеются полезные следствия. Как правило, эффектами объемного заряда можно пренебречь, поэтому электрический потенциал U ( x , y , z ) должен удовлетворять уравнению Лапласа Ur + U, + U = 0 (где нижние индексы для xx yy zz
U обозначают частные производные по соответствующим переменным). Поэтому если известна функция U0 (x, y ) = U (x, y ,0) — распределение электрического потенциала для плоскости симметрии OXY , но не известен сам электрический потенциал U (x, y, z), то проверка сводится к условию Vx, y: Uxx + Uy, < -s2 < 0 в случае положительно заряженных частиц и к условию Vx, y: Uxx + Uyy >+s2 > 0 в случае отрицательно заряженных частиц. Если же объемным зарядом p(x,y,z) пренебречь нельзя и электрический потенциал U (x, y, z) удовлетворяет уравнению Пу ассона Uxx + Uyy + Uzz = -4пр (предполагается отсутствие диэлектрической проницаемости среды), то проверка сводится к условию Vx, y:
U ° + U yy + 4 пр 0 < — s 2 < 0 в случае положительно заряженных частиц и к условию V x , y :
U x x + U yy + 4 np 0 >+ s 2 > 0 в случае отрицательно заряженных частиц (где р 0 ( x , y ) = р ( x , y ,0 ) — распределение плотности объемного заряда в плоскости симметрии).
Перед тем как приступить к доказательству теоремы, рассмотрим физический смысл сформулированного условия устойчивости пучка. Для простоты ограничимся положительно заряженными частицами. В силу симметрии электростатического потенциала выполнено условие Uz |_ п = 0 . Поэтому, во-первых, частица, стартующая в плоскости симметрии z = 0, продолжает движение в плоскости симметрии, а во-вторых, разложение потенциала при малых отклонениях от плоскости OXY имеет вид:
U ( x , y , z ) ~ U ( x , y ,0 ) + 2 z 2 UZZ ( x , y ,0 ) +
-
+ 724 z"U zzzx ( x , y ,0 ) + - ,
где разложение содержит только четные степени z в силу симметричности потенциала относительно плоскости OXY . Это означает, что в случае положительного значения коэффициента U z ( x , y ,0 ) при малых отклонениях z независимо от знака возникает электрическая сила eE Z = - e ( д U / 9z ) ~ - ezUzz ( x , y ,0 ) , возвращающая заряженную частицу в сторону к плоскости OXY . В случае же отрицательного значения коэффициента Uzz ( x , y ,0 ) при малых отклонениях z возникает электрическая сила, еще более уводящая частицу от плоскости OXY .
Само по себе наличие возвращающей силы в любой точке траектории, вообще говоря, не означает устойчивости движения, т. к. вполне возможны случаи, когда
-
а) возвращающей силы недостаточно, чтобы вернуть частицу к плоскости OXY ;
-
б) возвращающая сила слишком сильна, чтобы локализовать частицу в окрестности плоскости OXY , так что частица пересекает плоскость и уходит от нее вдаль с другой стороны плоскости симметрии;
-
в) происходит резонансная раскачка колебаний частицы относительно плоскости симметрии, когда за счет возвращающей силы, разнонаправленной с двух сторон от плоскости симметрии, части-
- ца многократно пересекает плоскость симметрии со все более возрастающей амплитудой колебаний.
Точно так же само по себе отрицательное значение Uz (x, y,0) не означает запрета на локали- зованность движения частицы в окрестности плоскости OXY , поскольку на некотором рас- стоянии уводящая от плоскости сила может смениться возвращающей силой (соответствующий пример будет рассмотрен ниже). Наконец, знак величины Uzz (x, y,0) может меняться вдоль траектории частицы, так что зоны локальной устойчивости сменяются зонами локальной неустойчивости и ответ на вопрос, каким будет совокупный эффект, требует отдельного скрупулезного исследования.
Для строгого доказательства нашей теоремы воспользуемся теоремой Чаплыгина о дифференциальных неравенствах [13]:
Теорема Чаплыгина . Пусть имеется обыкновенное дифференциальное уравнение n -го порядка f ( n ) - F ( t , f , f ' , . , f ( n - 1 ) ) = 0 для функции f ( t ) с начальными условиями f ( t 0 ) = f , , f ' ( t 0 ) = f , „., f ( n - 1 ) ( t 0 ) = f , ( n - 1 ) . Пусть также имеется функция g ( t ) , удовлетворяющая начальным условиям g ( 1 0 ) = f„ g ‘ ( 1 0 ) = f , -, g ( n - 1 ) ( 1 0 ) = f , ( n - 1 ) и неравенству g ( n ) - F ( t , g , g '^ ,g ( n - 1 ) ) > 0 на интервале t е [ t 0, T ] при t > t 0 (где T > t 0). Пусть, кроме того, функции f ( t ) и g ( t ) дифференцируемы и непрерывны вплоть до n -го порядка, а функция F ( t , f , f ' , . , f ( n - 1 ) ) и ее частные производные по аргументам f , f '^, f ( n - 1 ) ограничены для интересующих нас диапазонов значений f , f'^,f ( n - 1 ) и независимой переменной t . Тогда существует такое значение T 0 > t 0, T 0 < T , что для всех t е [ t 0, T 0 ] , t > t 0, выполнено неравенство g ( t ) > f ( t ) . Аналогично, если есть функция h ( t ) , удовлетворяющая начальным условиям h ( 1 0 ) = f , , h ‘ ( 1 0 ) = f , ■ ••, h ( n - 1 ) ( 1 0 ) = f , ( n - 1 ) и неравенству h ( n ) - F ( t , h , h ',..., h ( n - 1 ) ) < 0, то существует такое значение T 0 > 1 0, T 0 < T , что для всех t е [ 1 0, T 0 ] , t > 1 0, выполнено неравенство h ( t ) < f ( t ) .
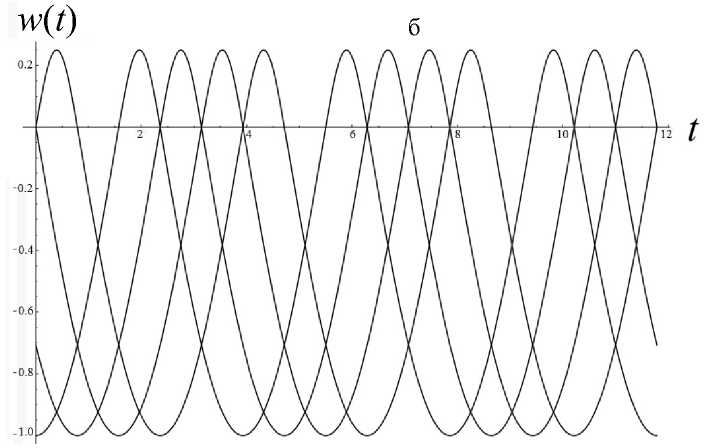
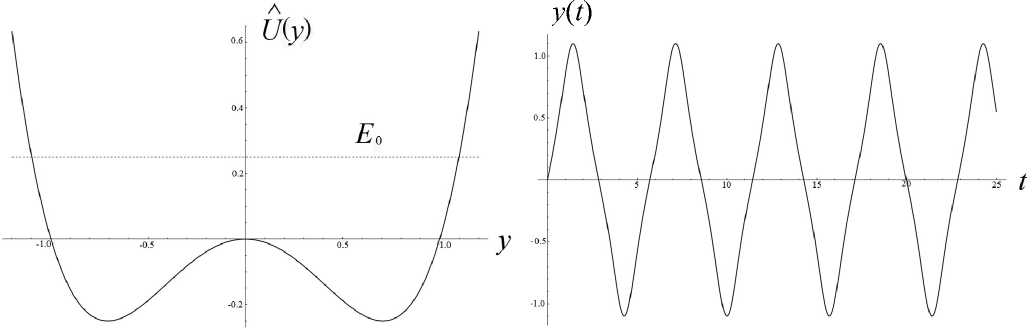
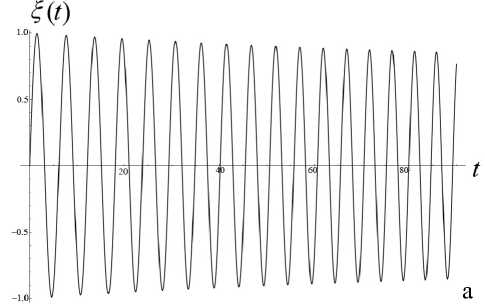
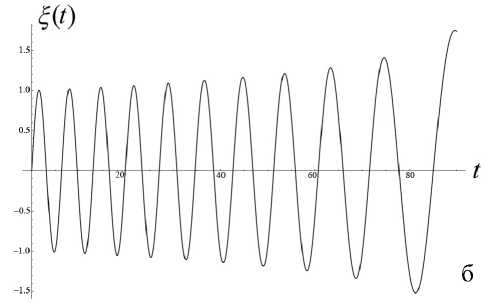
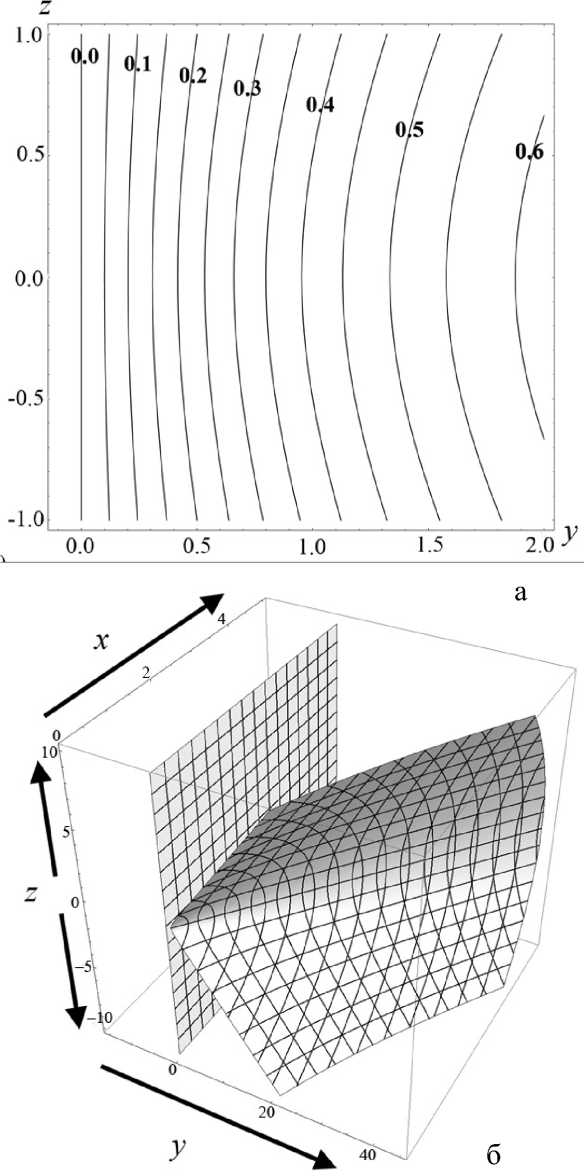
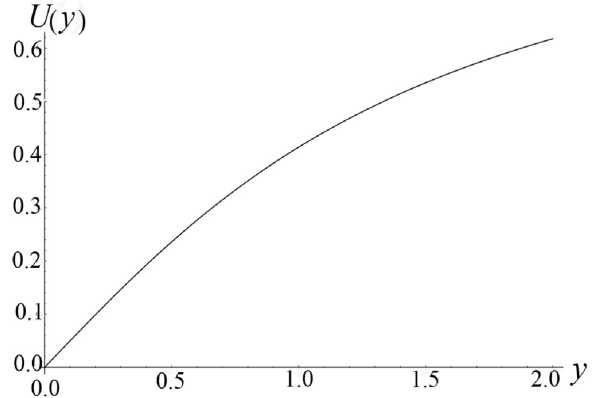
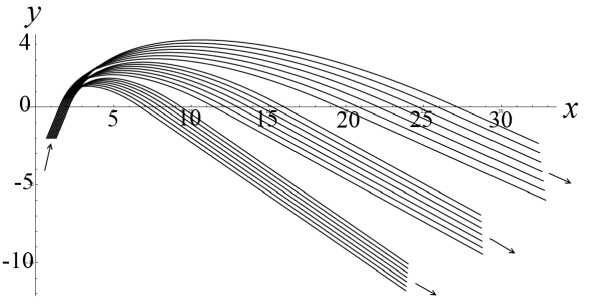
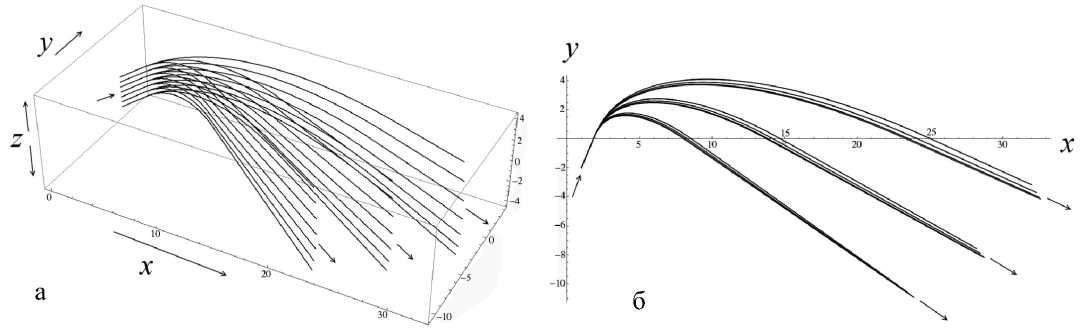
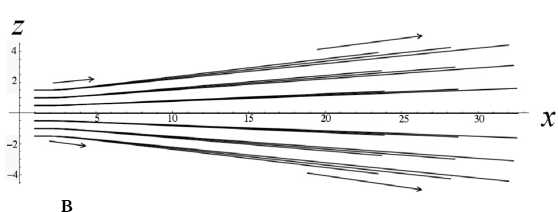
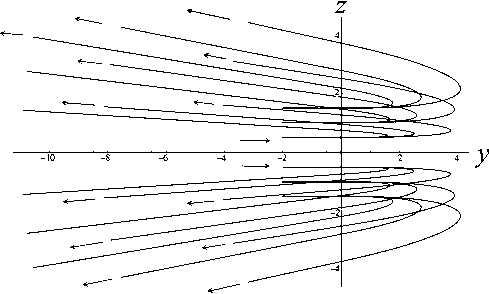
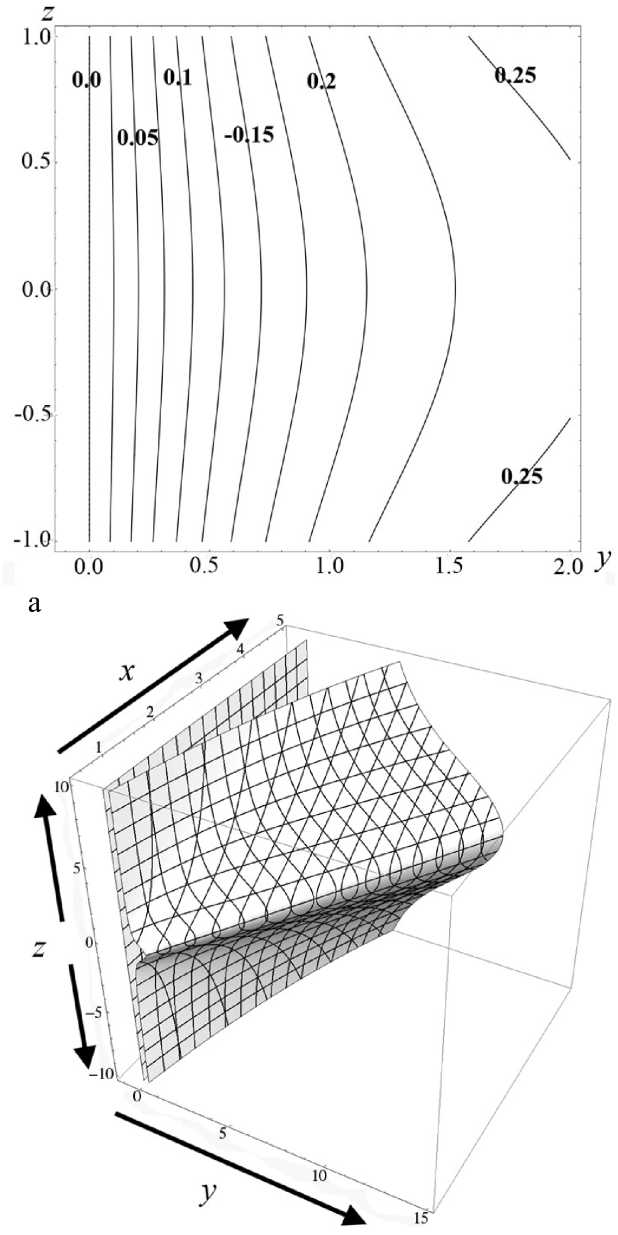
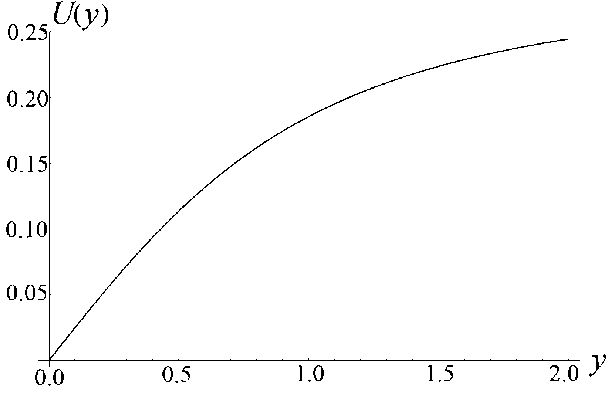
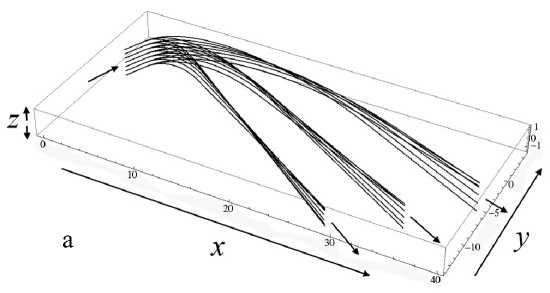
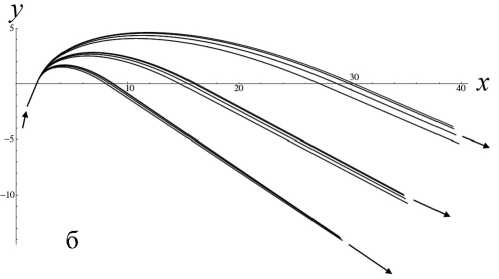
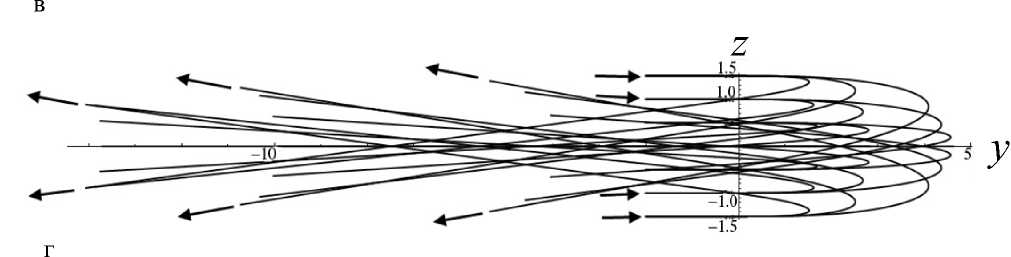
Теорема Чаплыгина может использоваться для оценки (мажорирования) решений дифференци- ального уравнения. А именно, пусть f (t) — решение уравнения f(n)= F(t,f,f'^,f(n-1)), g(t) — решение уравнения g(n )= G (t, g, g ',^, g(n 1)) = = 0, а h (t) — решение уравнения h(n ) = = H (t, h, h',^, h(n-1)) с одними и теми же начальными условиями. Если для интересующей нас области значений функций и независимого переменного выполнено неравенство H(t,10,t1,...,tn-1 )< Чаплыгина следует, что существует такое T0> 10 (возможно, равное бесконечности), что h (t )< f (t)< g (t) на рассматриваемом интервале t е [10, T0], t > 10. Искусство состоит в подборе таких функций G и H , чтобы, во-первых, соответствующие уравнения имели простые решения, во-вторых, чтобы функции G и H достаточно тесно "зажимали" между собой функцию F , в-третьих, чтобы критическое значение времени T0 , за пределами которого теорема Чаплыгина перестает быть верной, было расположено вне интересующего нас интервала времени. Примечание. Хотя теорема Чаплыгина и постулирует существование предельного значения T0 , выше которого рассматриваемые неравенства перестают быть справедливыми, но ее доказательство включает в себя вполне конструктивные средства для вычисления предельного значения T0 по заданному дифференциальному уравнению. Однако для нашей задачи это ограничение несущественно — как правило, предельное значение T0 много больше времени T движения заряженной частицы вдоль рассматриваемой траектории, поэтому в дальнейшем мы не будем делать разницы между T0 и T . Подробности см. в [13]. Приступим к доказательству нашей теоремы. Пусть x (t), y (t), z (t) — решение системы уравнений движения для положительно заряженной частицы с массой m и зарядом e mx" = - eUx (x, y, z), my" = - eUy (x, y, z), mz" = - eUz (x, y, z) с начальными условиями, лежащими в окрестности плоскости OXY . Зафиксируем функции x (t), y (t) и рассмотрим отдельно уравнение для функции z (t), которое при заданных x (t), y (t) становится самодостаточным: mz" = -eUz (x(t), y (t), z). (1) По условию теоремы для любых x, y , лежащих в области движения частицы, выполняется требование Uzz(x,y,0)>s2>0. Выберем диапазон значений переменной z g[0,h] достаточно малым, чтобы была справедлива оценка Vt g[tо, T], Vz g[0, h]: U (x (t), y (t),z)/z>S > 0, (2) либо в более сильной форме Vx,y g OXY, Vz g[0, h]: Uz(x,y, z)/z >S > 0. (2а) Это возможно, поскольку при z g [0, h] и h ^ 0 величина Uz ( x, y, z ) = z • Uzz ( x, y,0) + + 6 z 3 • Uzzz ( x, y,0) + "' = z • Uzz ( x, y,0) + 0 ( h 3 ) оказывается сколь угодно близкой к величине z • Uz (x,y,0). Поэтому величина Uz (x,y,z)/z будет регулярной функцией в окрестности точки z = 0, а поскольку в соответствии с заданным условием величина Uzz (x,y,0)> s2 > 0 положитель- на, (Uz (x, y, z)/z) при достаточ- то величина min zg[0,h] но малых h тоже обязана быть положительной. Очевидно, что существуют разнообразные сочетания h и εˆ , обеспечивающие выполнение оценки (2) или (2а), однако обсуждение оптимального подбора h и εˆ отложим до конца рассуждений. В результате можно определить верхние и нижние грани величины Uz (x, y, z)/z, каждая из которых будет положительной при выборе значения h достаточно малым: min (Ufxft),yU),z\lz\ = sfc2> 0, ;[0,h],tg[t0,T]V zv U-/V/’ ( Uz (x ( t) , y ( t), z)/z ) = A > 0, min zg[0,h], tg[t0,T] min (U, (x, y, z)/z) = eK2 > 0, zg[0,h], x,y■ oxy zV j Л' min (U (x, y, z)/z )= и2 > 0. zg[0,h], x,ygOXY^ ~ X Л '^h (3а) В таком случае Vz g[-h, + h ] (в силу симмет- ричности потенциала и соответственно антисимметричности компоненты напряженности поля Uz ) выполняются следующие оценки: Uz (x,y,z)> > z • £2Х при z > 0, Uz (x, y, z )< z • sh2 при z< 0, Uz (x, y, z )< z • uh при z > 0, Uz (x, y, z )>z • uh при z< 0. Пусть z0, z‘ — начальные условия для уравнения (1). Рассмотрим в качестве функций, используемых в теореме Чаплыгина, функции u (t) и w (t), имеющие те же начальные условия z0, z‘ и удовлетворяющие уравнениям mu" + eF(u)u = 0, mw" + eG(w)w = 0, (4) где положительные кусочно-постоянные функции F (z) и G (z) определены как F (z ) = :E; при z > 0, G. z U2 при z< 0; uh при z > o, 2 (5) sh при z< 0. Поскольку Vz g[-h, + h] Uz (x,y, z)>F (z)• z, Uz (x, y, z)< G (z)• z, то при сравнении уравнений (4) с уравнением (1) в соответствии с теоремой Чаплыгина получаем оценку w (t) < z (t) < u (t), t. e. |z(t)< max{|u(t),|w(t)}, если, конечно, u (t)g[-h,+h] и w (t)g[-h, + h ]. Однако функции u (t) и w (t), являющиеся решениями уравнений (4) с кусочно-постоянными функциями (5), — это кусочно-синусоидальные функции, глобально ограниченные по амплитуде пропорционально начальным условиям (ниже в статье приведены их графические образы). Поэтому всегда можно так масштабировать начальные условия z0, z0 (подобрать их достаточно маленькими), чтобы требования u(t)g[-h,+h] и w(t)g[-h, + h] были выполнены. На этом доказательство можно считать законченным: показано, что при выполнении условий теоремы и при достаточно малых возмущениях начальных условий пучка в перпендикулярном направлении траектории будут оставаться глобально локализованными в окрестности плоскости симметрии (в пределах z (t)g[-h, + h ]) в течение всего времени движения заряженных частиц. Сам же параметр h можно выбрать сколь угодно близким к нулю, так что при выборе возмущений начальных условий пучка в перпендикулярном направлении достаточно малыми пучок можно сделать сколь угодно тонким. Примечание. Для применения теоремы Чаплыгина также требуется, чтобы функции u (t) и w(t) были дважды непрерывно-дифференцируемы, что эквивалентно требованию, чтобы правые части как исходного дифференциального уравнения, так и дифференциальных уравнений, используемых для сравнения решений, были непрерывно-дифференцируемы. Для решений уравнений (4), представляющих собой кусочно-синусоидальные функции, и для кусочно-разрывных функций (5), используемых для правых частей уравнений (4), эти условия не выполнены. Однако этот момент не является принципиальным: функции (5) можно локально изменить в окрестности у = 0 таким образом, чтобы а) они стали непрерывными, б) сохранились неравенства Vz е[-h, + h ]: Uz (x, у, z )> F (z)• z, Uz (x, у, z )< G (z )• z, в) по крайней мере, на фиксированном интервале времени было обеспечено сколь угодно малое отклонение решений модифицированных уравнений (4) от кусочно-синусоидальных функций, соответствующих точным уравнениям (4). Рассмотрим теперь более подробно поведение решений уравнений (4), которые ограничивают в вертикальном направлении траектории возмущенного пучка. Пусть решение u (t) рассматривается на интервале времени, где оно удовлетворяет условию u (t) > 0. Для этого начальные условия z0, z‘ должны удовлетворять определенным требованиям: либо z0 > 0, а z‘ любое, либо z0 = 0, а z0 > 0. Если z0 > 0, то можно оттрасировать частицу назад по времени и найти момент времени, в котором будет выполнено условие z0= 0 (в силу колебательного характера функции u (t) такой момент времени обязательно существует). Поэтому без ограничения общности можно считать, что мажорирующее решение u (t) стартует с начальными условиями t = t0, z0= 0 и z0 = z‘> 0 . В таком случае u (t ) = ( z'o /®+) sin (®+( t -t0)), где ®+ = sh ^ejm , вплоть до пересечения оси u (t) = 0 и изменения знака в момент времени t1 = t0+ П®+. При этом в момент t = t1 изменения знака решения скорость u'(t) становится равной -z0, т. е. просто меняет знак по сравнению с начальной скоростью. Отрицательная полуволна решения конструируется аналогичным образом с заменой частоты ®+ на частоту ®- = цк ^e/m , а результирующая формула u (t ) = -( z0 /®_)х х sin (® (t -11)) будет справедлива вплоть до следующего изменения знака в момент 12 = t1 + П®- • После этого снова последует положительная полуволна u(t) = (z‘/®+)sin(®+(t-12)) и так далее. Решение является периодическим с периодом T = П®++ П®-. Максимум положительной полуволны равен, как легко видеть, величине + (z0 /®+), а минимум отрицательной полуволны равен величине -(z0/®_). В случае отрицательной начальной скорости отрицательная и положительная полуволны меняются местами. По той же схеме рассматривается поведение решения w(t). Вывод: решения z(t) для уравнений (1) ограничены полосой ±| z‘|/®+в окрестности плоскости OXY , заполняемой кусочно-синусоидальными решениями уравнений (4). Тем самым возмущенное движение оказывается ограниченным узкой окрестностью плоскости OXY , причем, как легко понять, ширина полосы стремится к нулю, когда возмущение начальных условий траектории z0, z‘ стремится к нулю. Подобные пучки, которые глобально локализованы в окрестности плоскости симметрии, а их толщина стремится к нулю при стремлении к нулю перпендикулярного возмущения начальных условий, будем называть плоскими. Чтобы завершить анализ, следует установить ограничения на возмущения начальных условий z0, z‘, при которых мажорирующие решения u (t) и w(t) оказываются ограниченны полосой z е[-h,+h], в пределах которой только и имеют силу сделанные оценки, а также соотнести начальные условия z0, z‘ с шириной полосы, в пределах которой лежит возмущенная траектория. Без ограничения общности можно считать, что либо z0 > 0, а z‘ любое, либо z0 = 0, а z‘ > 0 (в силу симметричности электрического потенциала при изменении знака начальных условий z0, z‘ траектория симметрично отражается относительно плоскости OXY ). При таких условиях начальная полуволна мажорирующей функции u (t), описываемой уравнениями (4), (5), является ее максимальной полуволной и совпадает с синусоидой, порожденной дифференциальным уравнением mu” + esh (u)u = 0 и записанной в виде аналитического решения как u (t) = z 0 cos (®+ (t- t0)) + (z ‘ /®+) sin (®+ (t- t0)) = = Vz02 +(z‘/®+)2 cos (®+ (t - t0) - arctg ((У0 /®+ )/У0 )), где ®+ = sh^e/m . Максимум + ^z2 +(z0 /®+)2 этой синусоиды и есть глобальный максимум верхней мажорирующей функции u (t). Соответственно минимум -^z2 +(z‘ 10+^2 этой синусоиды — это глобальный минимум функции w (t), ограничивающей решение z (t) снизу. В итоге неравенство -Vz2+(zо/°+)2 Графики решений u (t) и w (t) показаны на рис. 1. Рис. 1. Графики функций u(t) (а) и w(t) (б) при различных начальных условиях у 0, у0 при фиксированной энергии возмущения 7? = m(z0)2/2+ e(e2zо2/2), описывающей отклонение начальных условий от плоскости OXY Из "энергетического неравенства", в частности, становится понятно, как именно следует выбирать компромисс между величиной h и параметром εh для неравенства (2): надо максимизировать площадь эмиттанса допустимого возмущения z0, z0, описываемого неравенством m(z0)2/2 + e(shz2/2) < < e(s2h2/h). Задача поиска оптимальных параметров h и εh не вполне тривиальна, поскольку, приближая εh как можно ближе к нулю, мы увеличиваем h и тем самым увеличиваем диаметр фазового эллипса, равный его бóльшей полуоси. Но, с другой стороны, приближение εh как можно ближе к нулю уменьшает до нуля величину ю+, делая эллипс узким и сводя его площадь к нулю. Окончательная же оценка зоны устойчивости плоского пучка заряженных частиц получается объединением всех возможных эллипсов m(z0)2/h + e(shz2/h) (3), (3а) остается положительной. Примечание. Аналогичным образом можно было бы построить приближенные мажорирующие (снизу) решения для случая Uzz (x, y,0)<-s2 < 0. Однако результат оценки не будет работоспособным, поскольку соответствующие решения — экспоненциально растущие и быстро выходят за границы полосы z е [-h, + h ], в пределах которой сделанные оценки только и остаются справедливыми. При более детальном рассмотрении оказывается, что хотя условие Uzz (x, У,0)- s2 > 0 является достаточным для устойчивости плоского пучка, но обратное ему условие Uzz (x,y,0)<-s2 < 0 отнюдь не является достаточным для неустойчивости плоского пучка. В качестве примера на рис. 2 показаны осцилляции заряженной частицы в потенциальной яме с профилем U (z) = U0 (-Az2 + Bz4), которые являются глобально ограниченными по амплитуде, несмотря на условие Uˆzz I z=0 < 0. Следует, однако, заметить, что локальная ограниченность плоского пучка для этого случая несколько отличается от рассмотренного ранее случая. А именно, асимптотическая толщина пучка, отнюдь, не стремится к нулю при стремлении к нулю начального размера пучка, а стремится к вполне конечной величине, так что тонкий пучок на входе системы быстро превращается в тонкое кольцо конечного радиуса, а не в тонкую ленту. Аналогом этого эффекта является фиксированная ограниченность амплитуды при устойчивости в виде предельного цикла как противовес сколь угодно малой амплитуде при устойчивости в виде фокуса [14–20]. а б Рис. 2. Осцилляции заряженной частицы в потенциальной яме U (y) = U0(-Ay2+ By4). а — профиль потенциальной ямы и уровень полной энергии, соответствующий начальным условиям; б — нелинейные строго периодические осцилляции y(t), глобально ограниченные по амплитуде ЭНЕРГЕТИЧЕСКОЕ ОБОСНОВАНИЕ УСТОЙЧИВОСТИ И КОМПАКТНОСТИ ПЛОСКОГО ПУЧКА Если пренебречь математической строгостью, результаты предыдущего раздела могут быть обоснованы проще. Пусть отклонения z (t) от плоскости OXY имеют величину порядка λ, где λ — малый параметр. После подстановки z (X, t) = Xz1 (X, t) (где z1 (X, t)— функция порядка O (1) при X ^ 0) в силу симметрии электрического потенциала и, как следствие, в силу условия Uz\z 0 = 0, закон сохранения энергии можно записать как m (x,2 + y '2 + z '2) + eU (x, y, z) m (x '2+ y '2+ X2 z’2) + eU (x, y ,0) + + 2Xz12eUzz (x,y,0) + •••, а уравнения движения как mx" = - eUx (x, y, z) « «-eU, (x,y,0)-2Xz2 • eUxzz (x,y,0)--, my " = - eUy (x, y, z)« «-eUy (x,y,0)-2Xz2 • eUyzz (x,y,0)- •••, mz” = mXz’ = -eUz (x,y, z) « «-Xz. • eU7Ax,y,0)-—X3z3 • eU(x,y,0). 1 zz 1 zzzz Сохраняя в (7) члены не выше λ, а в (6) члены не выше λ2 (т. е. первые ненулевые поправки), получаем соотношения mx " = - eUx (x, y ,0), my" = -eUy (x, y,0), P= - p eUzz ( x, y,0) , (8) E = m (x'2 + y' 2) + eU (x, y ,0) + + X2 mz’2 +2z2eUzz (x,y,0) +O(X). Однако из первых двух уравнений (8) следует, m (x a + y '2) что E0 = —-— ---- + eU(x,y,0) — первый инте грал усеченных уравнений движения, поэтому ^2 (E - E0 ) = A W = λ = m2L- + 2 z12eUzz ( x, y,0) +O ( X ) = const. (9) Известно, что Vx, y: Uzz (x, y ,0 )>s2> 0, поэтому из условия (9) следует, что при ненулевых значениях zx, z‘ и достаточно малых X величина AE всегда положительна. В случае, когда известна априорная оценка 0 WW0, допустимые значения z1 и z‘, удовлетворяющие условию (9), образуют компактный эллипс, зависящий, впрочем, от текущих значений x (t), y (t). По результатам решения системы (8) z1 (t) и z‘(t) лежат в пределах 4-мерной полосы, составленной из фазовых эллипсов (9) для переменных z1, z‘ с центрами z1 = 0, z‘ = 0, которые размещаются в каждой точке x, y плоскости OXY . "Толщина" этой полосы определяется величиной AE = X2 -A W, которая представляет собой малую энергетическую поправку порядка λ2 , описывающую возмущение начальных условий движения в направлении, перпендикулярном плоскости OXY . Возвращаясь к переменным z (t), z' (t), из равенства (9) следует, что |z(t)| < ^2AE/(eUzz (x(t),y (t),0)) < V2AE/es2, т. е. представляет собой ограниченную величину порядка X при условии, что AE представляет собой величину порядка λ2 . Этот результат как раз и означает, что пучок заряженных частиц будет оставаться локализованным в окрестности плоскости OXY , если возмущение начальных условий, выводящее пучок за пределы плоскости OXY , достаточно мало. Уточним энергетическую оценку размера пучка с возмущенными начальными условиями. Пусть x (t), y (t), z (t ) = 0 — решение уравнений движения с начальными условиями x0, x0, y0, y0, z0 = = 0, z‘ = 0, лежащее целиком в плоскости симметрии z = 0. Добавим возмущение начальных условий в поперечном направлении: z0 = Xz0, z‘ = Xz0, где X — малый параметр. Представим решение трехмерной системы уравне- ний движения в виде ряда по малому параметру λ как x (к, t) = x (t) + kx1 (t) + к2x2 (t) + —, У (к, t) = y (t) + к^ (t) + к y 2 (t) + —, z(к, t) = kz1 (t) + к2z2 (t) + —. В силу симметричности электрического потенциала U (x, y, z) в разложении для x (к, t) и y (к, t) будут присутствовать только четные степени λ, а в разложении для z (к, t) будут присутствовать только нечетные степени λ . Ограничиваясь членами, не выше чем квадратичными, для закона сохранения энергии получаем соотношения: E = E0 + к2 E2+ к4 E4+ — = const, m (x,2 + y,2) E0 =-----2-----+ eU (x, y ,0), E2= mx'x2 + my'y2 + eUx (x, y,0) • x2+ + eUy ( x, y,0)^ y 2 + m^' + 2^ eUzz ( x, y,0)^ z12, m (x ‘2 + y ‘2) i E = + - eUx (x, y, 0) • x22 + 4 2 2 xx 2 + eUxy ( x, y,0)• x 2 y 2 +2 eUyy ( x, y,0)^ y 2, (Выражение для E4 является не вполне точным, поскольку должно содержать также и коэффициенты x4(t), y4(t), z3 (t) разложения решения в ряд по малому параметру λ, однако ранее мы договорились этими поправками пренебречь). Выражение для E2 описывает компактный эллипс для z1, z‘, если значения x2, y2 меняются в ограниченном диапазоне или если значения x2 , y2 пренебрежимо малы на фоне значений z1 (второе условие, конечно же, является более сильным, чем первое). Выражение для E4 описывает компактный четырехмерный эллипс для x2, y2, x‘, y\ и тем самым обеспечивает глобальную ограниченность для x2,y2,x2, y2 , если квадратичная форма Uxxx2 + 2Uxyx2y2+ Uyyy2 является положительно определенной. Это выполнено тогда и только тогда, когда Uxx > 0, Uyy > 0, 2 xx yy xy . Однако эти условия находятся в очевидном противоречии с условием Uxx + Uyy<-s2< 0 (в частности, поскольку Uxx< -£2- Uyy, то UxxUyy-Uxy< -е2Uyy-е2Uyy-Uxy< 0). Соответственно использованное ранее для доказательства глобальной ограниченности z1, z‘ предположение, что значения x2 , y2 меняются в глобально ограниченном диапазоне, оказывается под вопросом. Это не означает, что траектория будет неустойчивой, это лишь означает, что мы не можем вывести устойчивость траектории, исходя только из энергетических соображений. Кроме того, это наводит нас на мысль, что одновременная глобальная ограниченность возмущения траектории как внутри плоскости, так и перпендикулярно плоскости невозможна. Этот вывод будет почти очевидным, если мы вспомним, что электрический потенциал удовлетворяет уравнению Лапласа и тем самым не может иметь минимумов и максимумов, но лишь седловые точки. Опять-таки, отсутствие глобальной ограниченности траектории сразу во всех направлениях по отношению к отклонению пучка от плоскости симметрии не означает, что невозможно добиться фокусировки пучка по двум направлениям сразу: ничто не мешает возмущенным траекториям сперва расходиться, а потом снова сходиться в точку. Принципиальным вопросом, однако, является то, что, по-видимому, возмущенный пучок не может быть глобально узким вдоль базовой траектории по двум направлениям одновременно. Очевидный недостаток всех этих выкладок в том, что в качестве исходного предположения выбирается именно тот тезис ("малость" z (t) при всех t ), который требуется доказать. Достоинством же подхода, изложенного в предыдущем разделе, является не только математическая строгость выкладок, но и возможность конструктивно оценить полосу устойчивости движения в окрестности плоскости OXY , а также получить в явном виде зависимость толщины плоского пучка от энергии возмущения при отклонении частицы от плоскости OXY . ОЦЕНКА ЛОКАЛЬНОЙ ТОЛЩИНЫ ПУЧКА При разложении решения в ряд по малому параметру λ и представлении его в виде x (t) = kx1 (t) + к2 x2 (t) + —, y (t ) = kУ1 (t) + к y 2 (t) + —, z (t) = kz1 (t) + к2 z 2 (t) + — для функции z1 (t) получается самодостаточное дифференциальное уравнение mz" = = -eUzz (x(t),y(t),0)z1. Поэтому изменение во mz ‘2 . 1 2 времени энергии E(t)= 1 + — eU zzz1 для воз мущения, перпендикулярного плоскости симмет- рии, описывается уравнением E = —ez, х х(Uxzzx'(t) + Uyzzy'(t)). Считая, что z1 (t) меняется в ограниченных пределах, 0 max 1 max , так что можно, ин- тегрируя функцию времени f'(t ) = Uxzzx'(t) + +Uyzzy'(t) вдоль конкретной траектории, определить максимально достижимое значение энергии E (t) в каждый момент времени и тем самым максимальную толщину возмущенного пучка в каждой точке базовой траектории. Задача упрощается, если учесть, что для получения максимальной оценки значения энергии E(t) интегрировать функцию Uxzzx'(t) + Uyzzy'(t) следует лишь по тем участкам траектории, где эта функция положительна, и что функция f'( t ) = Uxzzx'( t ) +Uyzzy'( t ) — это производная по времени от функции f (t) = Uzz (x (t), y (t)). Поэтому интересующая нас вариация 5f (t) — это сумма приращений величины Uzz (x (t), y (t)) вдоль тех участков траектории, где функция f (t) = Uzz (x (t), y (t)) возрастает. Тем самым в каждой точке траектории мож- „ mz'2 , 1 2 но построить эллипс 1 +—eU zzz1< < E20 + ^е • 5f (t)Zmax (t) для допустимых значений z1, z‘, описывающий возможную толщину сопровождающего пучка в конкретной точке конкрет- п ту 0 mz , 1 тт 0 А2 ной траектории. Здесь E2 = + — eUzzz0 — это начальное значение величины E2 (t), описывающей энергию отклонения траектории от плоскости симметрии; Zmax (t) — оценка максимального по модулю значения z1 (t) на интервале времени от точки старта до текущей точки; а для сокращения обозначение записи введено новое U0 = Uzz(x0,y0,0). В свою очередь требуется оценка для величины Zmax (t) максимального отклонения траектории от плоскости симметрии между начальной и текущей точкой. Получение же самосогласованной оценки Zmax (t) представляется достаточно сложной задачей в рамках используемого здесь "энергетического" формализма, особенно если функция Uzz (x (t), y (t)) не является монотонной вдоль траектории и, как следствие, локальная амплитуда колебаний функции zx (t) также не является монотонной функцией. Если считать, что Uzz (x (t), y (t)) мало меняется на протяжении одной полуволны решения уравнения mz"=-eUzz (x(t),y (t),0)z1, то легко понять, что при локальном увеличении Uzz ампли- туда полуволны падает, а при локальном уменьшении Uzz амплитуда полуволны растет. В частном случае, если Uzz (x (t), y (t)) монотонно падает вдоль траектории, то 5 f (t) = 0 и значение Zmax (t) становится несущественным. Тем самым локальная оценка толщины пучка в заданной точке траектории вычисляется как zmax = 2E20 eeUzz , где E20 — это начальное значение энергии ET2 (t) для отклонения траектории от плоскости симметрии. Как и следовало ожидать, эта функция монотонно растет вдоль траектории в силу монотонного убывания Uzz (хотя с учетом того, что E2 (t) — монотонно убывающая функция, данная оценка слегка завышена). Ожидается, что для монотонно растущей функции f (t) = Uzz (x (t), y (t)) амплитуда колебаний z (t) будет монотонно падать по ходу траектории (более-менее строгое обоснование этого факта см. далее), поэтому максимальное значение амплиту- ды колебаний Zmax (t) = E0 достигается в начальной точке, вариация энергии E2 (t) равна 5 f (t) = Uzz (x (t),y (t))- U°0Z, а оценка для толщины пучка в заданной точке траектории сводится к неравенству zmax< 2E20]eU°zz , соответствующему оценке амплитуды колебаний функции z1 (t) в начальной точке. Данная оценка является основательно завышенной и не соответствует нашим ожиданиям, что толщина пучка должна падать вдоль длины траектории при монотонно растущей функции Uzz . Тем не менее эта весьма грубая оценка правильно описывает глобальную ограниченность пучка и стремление толщины пучка к нулю при стремлении к нулю энергетического возмущения, связанного с отклонением начальных условий от плоскости симметрии. Более содержательную информацию о поведении толщины пучка, т. е. об амплитуде колебаний функции z1 (t) вдоль рассматриваемой траектории, можно получить, аккуратно проанализировав параксиальные уравнения траекторий.*) Один из способов это сделать — использовать подстановку Крылова—Боголюбова [21–24]. При применении этой процедуры уравнение mz1" = -eUzz (x(t),y(t),0)z1 для параксиального решения z1 (t) удобно записать в виде системы z' = ri, ri =- z1 (Y 2 + Xf (t)), где X — малый параметр, y2 > 0 — оценочное значение величины (e/m)Uzz (x(t),y(t),0) вдоль конкретной базовой траектории; а медленно меняющаяся во времени величина Xf (t) описывает изменение (e/m) Uzz (x (t), y (t) ,0) вдоль выбранной базовой траектории по отношению к ее оценочному значению y2 > 0. После этого решение для (10) ищется в форме z1 (t) = exp A(t)• sin ф(t), r1 (t ) = y exp A (t )• cos ф( t), где A (t) и ф (t) — две новые функции, однозначным образом связанные с прежними функциями z1 (t) и r1 (t). После элементарных выкладок для функций A (t) и ф( t) получаются уравнения λ A(t 1 2- f(t) smM t), γλ (11) ф' (t ) = Y + -f (t) sin2 ф( t). γ Остается представить функции A(t) и ф(t) в виде рядов по малому параметру λ таким образом, чтобы нулевое приближение соответствовало точному решению системы z‘ = r1, r1' = -y2z1, получающейся при X =0: A (t ) = A0 + XA1 (t) + X2 A2 (t) + -•, ф (t ) = ф0 + Yt + Xф1 (t) + X2ф2 (t) + —. В результате получается цепочка уравнений ф‘ (t ) = Y f (t) sin2 (Yt + фо ), A (t) = -2Y f (t) sin (2Yt + 2фо); ф2 (t) =1f (t )ф1 (t) sin (2Yt + 2фо), γ A 2(t) = -1f(t) ф1(t) cos (^ + 2ф0); • • •, или с учетом того, что ф1 (10) = 0, A1 (10) = 0, ф2(10) = 0, A2(10) = 0, „., цепочка рекуррентных формул 1t ф1 (t) = - Jf (t) sin2 (Yt+ фо) dt, γt0 1t A (t) = -—J f (t) sin(2Yt + 2фо) dt; 2γt0 ф2 (t) =1j f (t) ф1 (t) sin (2Yt + 2фо) dt, γt0 A2 (t) = -1J f (t) ф1 (t) cos (2Yt + 2фо) dt; γt0 откуда сперва можно получить решения для поправочных членов A1 (t) и ф1 (t), потом для поправочных членов A2(t) и ф2(t), и т. д. В случае, когда за период T = k]y изменение функции f (t) мало (функция является "медленной" по сравнению с частотой колебаний), при интегрировании выражений (12) функцию f (t) можно вынести за знак интеграла. Более аккуратные результаты можно получить с помощью формулы интегрирования по частям [25]: tt j f (т)F(т)dT = f (t)Fi (t)- j f '(T)Fi (T)dT = t0 t0 t = f (t)Fi (t) - f ‘(t)F2 (t) + j f "(t)F2 (t)dT = t0 = f (t)Fi (t)-f ‘(t)F2(t) + t + f"(t) F3 (t )-j f ”(t ) F3 (t ) dT = •, (13) t0 где Fk (t )=[ t F--i (t) dT, F (t ) = F (t) —повтор-t0 ные интегралы от функции F (t), обращающиеся в ноль при t = t0. Если f (t) — "медленная" функция по сравнению с рассматриваемым масштабом времени, ее производными начиная с некоторого номера можно пренебречь и тем самым из формул (13) можно корректным способом вывести удобные приближенные выражения для решений системы (12). Точку отсчета t0 = 0 удобно сместить так, что начальная фаза ф0 = 0. Тогда формулы (12) в сочетании с (13) дают приближенные решения t (. sin2Yt1 ф (t ) =—f (t) 1 - - 2Y I 2Yt J - 21 f •( t F - 1-222222 L 4y k 2y212J ^ + (t )fi - Si^Yt 1, 2Y k 2/t J A(t ) = -4ч f (t) sin2Yt+ 2γ2 Рис. 3. Осцилляции решений линейного дифференциального уравнения ^"(t) = -^(t)(1 + at) с нормированными начальными условиями ^ (0)= 0, ^'(0) = 1 при (а) a = +0.01 и (б) a = -0.01 +f,(- t )(1 sin 2γt 2γt + — -27 f (t) sin2Yt, Соотношения (14), в частности, подтверждают тот факт, что с адиабатическим увеличением значения Uz (т. е. при f (t)>0) локальная амплитуда колебаний exp A (t) падает, а с уменьшением (т. е. при f (t)< 0) — растет. Локальная частота 69(t) = (ф(t)-ф0)]t, как легко видеть, ведет себя прямо противоположным образом. Для иллюстрации на рис. 3 приведены графики решений нормированного уравнения ^"(t) = -^(t)(1 + at) при положительных и отрицательных значениях параметра σ , которые для этого частного случая могут быть выражены в аналитической форме через специальные функции. Альтернативный вариант — использование метода ВКБ (Вентцеля—Крамерса—Бриллюэна) [26], который обычно применяется для решения уравнения Шредингера. А именно для уравнения (10), записанного в форме z"=-z1 (Y2+ Xf (t)), при условии положительности значения Y2 + X f (t) решение ищется в виде z1 (t) = exp (i у (t)). После этой подстановки урав- нение приобретает вид -(у '2) +iу'' + + (y2 + Xf (t)) = 0. Предполагая, что у" мало по сравнению с остальными членами (т. к. при X ~ 0 у точного решения имеем у"«0), получаем в первом приближении у' = ±^y2 + X f (t), у = ±J y 2 + X f (t)dt. Два разных знака соответствуют двум независимым приближенным решениям, и при переходе к исходному линейному дифференциальному уравнению для z1 (t) эти два решения должны быть скомбинированы в одно решение общего вида в виде линейной суперпозиции двух независимых решений. Однако, как легко видеть, это решение слишком грубое и не отражает всех особенностей ожидаемого поведения функции z1 (t): в частности, при медленном изме- нении y2 + Zf (t) вдоль невозмущенной траектории меняется локальная частота осцилляций, но не их амплитуда. Условие применимости полученного приближения (малость /") выглядит как /'V 1 Zf't t) 2 7y2+zf(t) << y 2 + Z f (t). Это позволяет найти более точное приближение, а именно, пред- „ L 1 Zf'(t) положив, что / ®±--, — 2 7 y 2+м (t) , уравнение для функции / (t) дает уточненное решение в виде /1 . Y 2 + Zf (t )± 1 -f^T , 2VY +Zf (t) / ~ ± J y2+ Zf (t) + - f (t) , V 4 Y2 + Zf (t) / (t )~±J 7 Y2 + Zf (t)dt + -4-ln ( y 2 + Zf (t)) (фактически здесь использован еще один шаг итерационного уточнения решения, когда от предыдущей итерации берется значение /" и с помощью квадратур вычисляется новое значение / (t)). Возвращаясь к функции z1 (t) и комбинируя независимые решения, соответствующие разным знакам перед корнем, получаем приближенное решение ------------X ( y 2 + Zf (t))'« X^Ca exP (+iJ 7y2 + Z f (t)dt) + +C exp (-iJ 7y2 + Z f (t)dt) j « C0 ( y2+ Zf(t)) 1 4 sin которое адекватно описывает изменение амплитуды и частоты локальных колебаний функции z1 (t) при медленном изменении величины у2 + Zf (t) вдоль базовой траектории. Более детальное рассмотрение данного вопроса выходит за рамки задачи, поставленной в этой статье. ПРИМЕР. ЭЛЕКТРОСТАТИЧЕСКИЕ ЗЕРКАЛА С ПОТЕНЦИАЛАМИ ДОНКИНА В качестве примера рассмотрим системы с электростатическими полями, синтезированными на основе формулы Донкина [10–12]. А именно рассмотрим электростатические потенциалы U (x, y, z), которые представляют собой функцию, однородную по Эйлеру с показателем однородности, равным нулю: VZ, Vx, y, z: U (Zx, Zy, Zz) = U (x, y, z). Подобные потенциалы обладают специфическими полезными электронно-оптическими свойствами [10–12, 27–30]. В силу того, что потенциалы U (x, y, z) должны удовлетворять уравнению Лапаласа Uvv + U,„, + U, = 0, можно показать, что любой xx yy zz такой потенциал можно выразить с помощью формулы ([31, пример 23 к главе 18]): U (x, y, z ) = = U 0 F , y , 2 ,,2 72 ^ x + x л + y + z z x + 7 x2+ y2+ z2 , (15) где F (p, q) — надлежащим образом выбранная гармоническая функция, т. е. функция, удовлетворяющая двумерному уравнению Лапласа Fpp + Fqq = 0. Легко проверить, что при произвольной гармонической функции F (p, q) электрический потенциал (15) будет удовлетворять трехмерному уравнению Лапаласа и при этом будет представлять собой функцию, однородную по Эйлеру с показателем однородности, равным нулю. Для того чтобы электрический потенциал (15) был симметричен относительно плоскости z = 0, необходимо и достаточно, чтобы функция F (p, q) была четной по аргументу q . Для того, чтобы электрический потенциал (15) был антисимметричен относительно плоскости y =0 и чтобы соответственно плоскость y = 0 могла использоваться как входной (заземленный) электрод электростатического зеркала, необходимо и достаточно, чтобы функция F (p, q) была нечетной по аргументу p. Простейший электрический потенциал вида (15) получается при выборе F (p, q) = p (как легко видеть, эта функция одновременно и четна по аргументу q , и нечетна по аргументу p ). В [11, 12] в качестве одного из примеров электроннооптических систем на основе потенциалов, основанных на формуле Донкина, рассматриваются Рис. 4. Эквипотенциальные линии и эквипотенциальные поверхности для электрического потенциала (16). а — эквипотенциальные линии в сечении OYZ при x = 1; б — эквипотенциальные поверхности (полезадающие электроды) для значений потенциала U = 0.0 и U = 0.9 электростатические зеркала, описываемые потенциалом U0y U (x, y, z ) = < x + Jx2 + yг + z z при y > 0, 0 при y< 0. Эквипотенциальные линии и эквипотенциальные поверхности для электрического потенциала (16) в сечениях x = 1 и z = 0 показаны на рис. 4. (Трехмерные эквипотенциальные поверхности для потенциалов вида (15) представляют собой конические поверхности с центром в начале координат и проходящие через эквипотенциальные линии в фиксированном сечении x = const). На рис. 5 показан профиль электрического потенциала (16) при фиксированных значениях x = 1, z = 0 по мере углубления во внутреннюю область зеркала (т. е. при возрастании координаты y ), из которого следует, что при U0 > 0 на положительно заряженные частицы электрическое поле (16) действует, как зеркало. На рис. 6 показаны траектории ионов в плоскости симметрии OXY этого электростатического зеркала. Как и следует из общей теории [10–12], Рис. 5. График распределения электрического по тенциала (16) вдоль прямой линии x = 1, z = 0 Рис. 6. Три параллельные моноэнергетические пучка, двигающиеся в плоскости OXY и отклоняемые зеркалом на основе электрического поля с потенциалом (16) на разные углы в зависимости от энергии б входной моноэнергетический пучок параллельных траекторий преобразуется в выходной пучок параллельных траекторий, где угол поворота и точка выхода пучка из зеркала зависит от энергии пучка, а степень сжатия пучка определяется законом подобия траекторий, характерным для потенциалов Донкина. Однако для потенциала (16) величина (U,x + Uyy )| =---------Uoy-------- ( )z=0 7X277 (x+7X277 )2 является строго положительной в области у > 0 и, как результат, следует ожидать неустойчивость траекторий при отклонении частиц от плоскости симметрии. Этот факт иллюстрируется на рис. 7, где показаны траектории с одинаковыми начальными координатами и углами в плоскости OXY , смещенные в начальный момент вдоль оси OZ с сохранением прежнего направления скорости, которые монотонно расходятся. Этот недостаток можно исправить, если в формуле (15) использовать более сложные гармонические функции F (p, q), обеспечивающие отрицательный знак для значения (Uх + U„„) . Так, выбе- xx уу z=0 рем в качестве прародителя гармоническую функцию F(Р,q) = || arctg к к / лк p I I p I 1 + arctgl I 1+q J к1 - q)) -p . Такой выбор соответствует электростатическому зеркалу с электрическим потенциалом U (x, у, z ) = < y Uо arctg- x ^ к 2У ' x2 + у2 + z2 J при у > 0, (17) при у< 0. Рис. 7. Траектории заряженных частиц в электрическом поле с потенциалом (16), которые стартуют с тремя разными энергиями и со смещениями по вертикали вдоль оси OZ . а — трехмерные траектории; б — проекция на плоскость OXY ; в — проекция на плоскость OXZ ; г — проекция на плоскость OYZ г Легко проверить, что для симметричного по z электрического потенциала (17) значение (' + Uy ) — 2U0y x2 + ~ f z=0 Рис. 8. Эквипотенциальные линии и эквипотенциальные поверхности для электрического потенциала, порожденного функцией (17). а — эквипотенциальные линии в сечении OYZ при x = 1; б — эквипотенциальные поверхности (полезадающие электроды), соответствующие значениям потенциала U = 0 и U = 0.3 будет строго отрицательным при U0 > 0 и у > 0, т. е. что достаточный критерий устойчивости плоского пучка для электрического потенциала (17) выполняется. На рис. 8 для двумерных сечений x = 1 и z = 0 показаны эквипотенциальные линии электрического потенциала (17). На рис. 9 показан профиль этого потенциала вдоль линии x = 1, z = 0 при возрастании координаты y , из которого следует, что на положительно заряженные частицы при U0> 0 это электрическое поле будет действовать как зеркало. На рис. 10 показан стартующий в плоскости OXY и отражаемый зеркалом параллельный пучок траекторий с тремя разными энергиями, целиком лежащий в плоскости OXY , для которого начальные координаты смещены друг от друга вдоль оси OX . Из рисунка видно, что, как и должно Рис. 9. График распределения электрического потенциала, порожденного функцией (17), вдоль прямой линии x = 1, z = 0 Рис. 10. Три параллельные моноэнергетические пучка, двигающиеся в плоскости OXY и отклоняемые зеркалом на основе электрического поля с потенциалом (17) на разные углы в зависимости от энергии быть в соответствии с теорией, входной моноэнер-гетический параллельный пучок, лежащий в плоскости симметрии OXY , преобразуется в выходной параллельный пучок, лежащий в плоскости симметрии OXY , причем угол поворота пучка зависит от его энергии. На рис. 11 показаны траектории с тремя разными энергиями и фиксированными начальными условиями в плоскости OXY , у которых начальные координаты смещены по оси OZ . Видно, что по сравнению с рис. 7, в, где траектории последовательно расходятся в вертикальном направлении, на рис. 11, в, имеется промежуточная фокусировка траекторий в вертикальном направлении (положение кроссовера для траекторий с разными энергиями, естественно, разное). УСТОЙЧИВОСТЬ И КОМПАКТНОСТЬ ПЛОСКОГО ПУЧКА В МАГНИТОСТАТИЧЕСКИХ ПОЛЯХ С ПЛОСКОСТЬЮ СИММЕТРИИ Рассматриваемая теорема может быть расширена для движения заряженных частиц в симметричном магнитном поле, а также в совмещенных симметричных электрических и магнитных полях. Пусть индукция магнитного поля B(x,y,z)=-УФ(x,y,z) задана с помощью скалярного магнитного потенциала Ф(x,y,z) [1], для которого плоскость OXY (т. е. z = 0) является Рис. 11. Траектории заряженных частиц в электрическом поле с потенциалом (17), которые стартуют с тремя разными энергиями и со смещениями по вертикали вдоль оси OZ . а — трехмерные траектории; б — проекция на плоскость OXY ; в — проекция на плоскость OXZ ; г — проекция на плоскость OYZ плоскостью антисимметрии: Ф(x,у,-z)—-Ф(x,у,z). Движение заряженной частицы в электромагнитном поле [32] без учета релятивистских или квантовых эффектов описывается уравнениями движения Ньютона mr — eE(r) + (e/c)|rx B(r)J, или в скалярных обозначениях dx — — P, dt dp ee — —-Ex (x,у,z)+—I qBz (x,у,z)-rBY(x,У,z)|, dt mmc dy —q, dt(18) dq ee — =-EY ( x У, z ) + I-pBz ( x У, z ) + B ( x У, z )|, dt mmc dz T — r, dt dr ee — —-EZ (x у,z)+—I PBY (x у, z)-qBx (x у, z )|, dt mmc где x, y, z — декартовы координаты частицы; x (t), у (t), z (t) — траектория частицы; p (t), q (t), r (t) — компоненты скорости частицы; m — масса частицы; e — заряд частицы; t — время; E(x, у, z, t) —(EX,EY, EZ) — напряженность электрического поля в точке x, y, z в момент времени t; B (x, у, z, t) —(BX, BY,Bz) — индукция магнитного поля в точке x, y, z в момент времени t ; Ex — -ди/9x ; EY — -дU/9у ; EZ — -дU(9z ; BX —-дФ/дx ; BY —-дФ/ду ; BZ —-дФ/дz ; U (x, у, z) — скалярный электрический потенциал, удовлетворяющий условию симметрии U(x,у,-z) — U(x,у,z); Ф(x,у,z) — скалярный магнитный потенциал, удовлетворяющий условию антисимметрии Ф( x, у, -z) — -Ф(x, у, z). Как и раньше, заряженные частицы, стартовавшие в плоскости OXY , будут оставаться в ней, поскольку в плоскости OXY в силу антисимметричности скалярного магнитного потенциала Ф выполнены условия BX (x,у,0) = 0, BY (x,у,0) = 0, а в силу симметричности скалярного электрического потенциала U — условие EZ (x, у,0) = 0. При малых отклонениях от плоскости OXY уравнения движения заряженной частицы вдоль координаты z принимают вид: dz T = r, dt dr e f д2U d2U 1 f dBZ dBZ )) ”z■- 1 1 p^q^" I dt m ^ dx dу c ^ dу dx )) поскольку с учетом того, что электрический скалярный потенциал U (x, у, z) разлагается в окрестности точки z = 0 по четным степеням z, магнитный скалярный потенциал Ф(x,у,z) разлагается в окрестности точки z = 0 по нечетным степеням z и дФ(x, у, z)/дz = -Bz (x, у, z), выполнены приближенные соотношения: , Z_дU (x, у, z) a 2U (x, у,0) = dz *"zd fs2U(x,у,0) a2u(x,у,0), =z ■ i ax ау) x_ 9ф(x,у,z) а2ф(x,у,0) B —--^ - z--------- dxd = z 9Bz (x, у,0) dx дФ( x, у, z) д 2Ф( x, у ,0) BY —--® - z---------- ду дудz = z 9Bz (x,у,0) ду Как и для чисто электрического поля, согласно уравнениям (19), при малых отклонениях частицы от плоскости симметрии возникает сила, пропорциональная z , направление которой зависит от знака выражения I (x, у) f92U (x, у ,0)+a2U(x,y,0) + v 9x 2 ду2 1 f , ,9Bz (x,у,0) +" P (x, у)---- c l ду — q (x, у) 9Bz (x, у ,0) 9x , (20) z—0 где p (x, у) и q (x, у) — скорости p (t) и q (t), "приписанные" к точкам x(t), у (t) базовых траекторий, плотно заполняющих соответствующую подобласть плоскости OXY , так что каждой рабочей точке x, y соответствует некоторое допустимое множество скоростей. Поэтому, будет ли пучок, описываемый уравнениями (19), плоским целиком, определяется знаком величины (20). А именно, для того чтобы пучок был плоским, т. е. локализованным в окрестности плоскости OXY , для положительно заряженных частиц достаточно выполнения условия Vx,y,p(x,y),q(x,y):I<-s2 <0, а для отрицательно заряженных частиц — условия Vx,y,p(x,y),q(x,y):I>+s2>0. Строгое доказательство достаточности этого критерия совершенно аналогично электрическому случаю. Как и в чисто электрическом случае, величина (20) зависит от данных электромагнитного поля, заданных исключительно в плоскости симметрии, — распределения электрического потенциала U0(x, y ) = U (x, y,0) и распределения нормальной компоненты индукции магнитного поля BZ (x, y ) = BZ (x, y,0). В отличие от чисто электрического поля, в выражение (20) входят еще и скорости заряженных частиц в соответствующих точках базовых траекторий, поэтому для одних семейств траекторий движение может оказаться плоским, а для других — нет. КВАЗИСТАТИЧЕСКИЕ ЭЛЕКТРИЧЕСКИЕ И МАГНИТНЫЕ ПОЛЯ С ПЛОСКОСТЬЮ СИММЕТРИИ Как легко понять, все эти выкладки остаются практически без изменений, если рассматриваются меняющиеся во времени симметричные электрические потенциалы U (x, y, z, t) и антисимметричные магнитные потенциалы Ф( x, y, z, t), удовлетворяющие условию квазистатичности, т. е. когда напряжения на электродах и токи в катушках должны меняться достаточно медленно, чтобы в уравнениях для электромагнитного поля можно было пренебречь максвелловскими эффектами. Физический смысл "медленности" (а именно за время распространения электромагнитного возмущения — со скоростью света (!) — между электродами и катушками напряжения и токи для электродов и катушек должны меняться незначительно) показывает, что все используемые на практике электронно-оптические и ионнооптические приборы, включая радиочастотные квадруполи и аналогичные им устройства, вполне могут рассматриваться в качестве квазистатиче-ских. Посвящение. Лицензионная чистота Авторы посвящают эту работу памяти Юрия Константиновича Голикова, создателя и бессменного руководителя аналитической школы оптики заряженных частиц, к которой оба автора имеют честь и cчастье принадлежать (в [33] — интернет-адрес списка трудов Ю.К. Голикова). При выполнении моделирований траекторий и создании рисунков для данной публикации использовалась лицензионно-чистая программа Wolfram Mathematica версии 9.0 [34], приобретенная одним из авторов, и свободно распространяемая программа для редактирования растровых изображений Paint.NET версии 3.5 [35].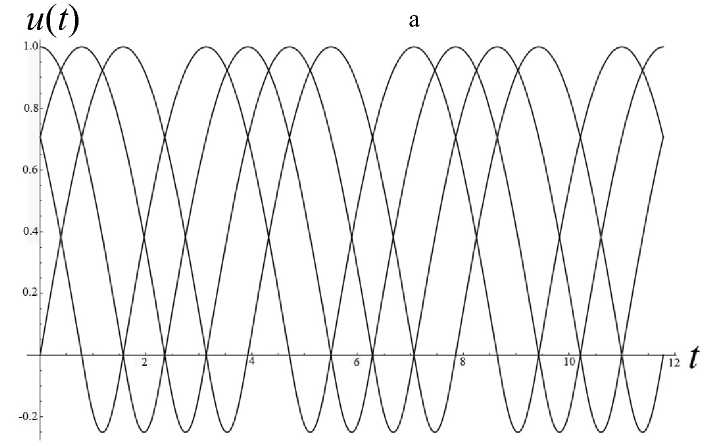


Список литературы Достаточный критерий устойчивости и компактности плоских ионных пучков в трехмерных электрических и магнитных полях с плоскостью симметрии
- Голиков Ю.К., Уткин К.Г., Чепарухин В.В. Расчет элементов электростатических электронно-оптических систем. Учебное пособие. Л.: Изд-во ЛПИ им. М.И. Калинина, 1984. 80 с.
- Голиков Ю.К., Соловьев К.В. Электростатические ионные ловушки. Санкт-Петербург: Изд-во Политехнического университета, 2008. 153 с.
- Голиков Ю.К., Краснова Н.К. Теория синтеза электростатических энергоанализаторов. Санкт-Петербург: Изд-во Политехнического университета, 2010. 409 с.
- Голиков Ю.К. Энергоанализирующие свойства электростатических полей с плоскостью симметрии. Дис. … канд. физ.-мат. наук по спец. 01.04.04. Л.: ЛПИ им. М.И. Калинина, 1977. 105 с.
- Чепарухин В.В. Некоторые вопросы теории синтеза электростатических дисперсионных энергоанализаторов. Дис. … канд. физ.-мат. наук по спец. 01.04.04. Л.: ЛПИ им. М.И. Калинина, 1979. 132 с.
- Голиков Ю.К. Определение электростатических полей по заданным характеристикам движения заряженных и дипольных частиц. Дис. … д-ра физ.-мат. наук по спец. 01.04.04. Л.: ЛПИ им. М.И. Калинина, 1985. 254 с.
- Спивак-Лавров И.Ф. Корпускулярная оптика статических ионно-оптических систем со средней плоскостью. Дис. … д-ра физ.-мат. наук по спец. 01.04.04. Актюбинск, 1999. 232 с.
- Соловьев К.В. Псевдооднородные электромагнитные структуры в инструментальной электронной оптике. Дис. … канд. физ.-мат. наук по спец. 01.04.04. Санкт-Петербург: Санкт-Петербургский политехнический университет, 2004. 185 с.
- Саулебеков А.О. Электронно-оптические свойства некоторых осесимметричных электростатических полей и разработка на их основе энергоанализаторов для исследования поверхности твердого тела. Дис. … д-ра физ.-мат. наук по спец. 01.04.04. Алматы, 2007. 216 с.
- Краснова Н.К. Теория и синтез диспергирующих и фокусирующих электронно-оптических сред. Дис. … д-ра физ.-мат. наук по спец. 01.04.04. Санкт-Петербург, Санкт-Петербургский политехнический университет, 2014. 259 с.
- Габдуллин П.Г., Голиков Ю.К., Краснова Н.К., Давыдов С.Н. Применение формулы Донкина в теории энергоанализаторов I//Журнал технической физики. 2000. Т. 70, № 2. С. 91-94.
- Габдуллин П.Г., Голиков Ю.К., Краснова Н.К., Давыдов С.Н. Применение формулы Донкина в теории энергоанализаторов II//Журнал технической физики. 2000. Т. 70, № 3. С. 44-47.
- Чаплыгин С.А. Новый метод приближенного интегрирования дифференциальных уравнений. М.-Л.: ГИТТЛ, 1950. 103 с.
- Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. М., 1959. 916 с.
- Андронов А.А., Леонтович Е.А., Гордон И.И., Майер А.Г. Качественная теория динамических систем второго порядка. М.: Наука, 1967. 568 с.
- Андронов А.А., Леонтович Е.А., Гордон И.И., Майер А.Г. Теория бифуркаций динамических систем на плоскости. М.: Наука, 1967. 487 с.
- Блакьер О. Анализ нелинейных систем. М.: Мир, 1969. 400 с.
- Арнольд В.И. Геометрические методы в теории обыкновенных дифференциальных уравнений. Ижевск: РХД, 1999. 400 с.
- Арнольд В.И., Афраймович В.С., Ильяшенко Ю.С., Шильников Л.П. Теория бифуркаций//Сб. "Динамические системы", серия "Итоги науки и техники. Современные проблемы математики. Фундаментальные направления". Т. 5. М.: ВИНИТИ, 1986. С. 5-218.
- Марсден Дж., Мак-Кракен М. Бифуркация рождения цикла и ее приложения. М.: Мир, 1980. 368 с.
- Крылов Н.М., Боголюбов Н.Н. Новые методы нелинейной механики. М.-Л.: Гостехтеориздат, 1934. 243 с.
- Крылов Н.М., Боголюбов Н.Н. Введение в нелинейную механику. Киев: Изд-во АН УССР, 1937. 365 с.
- Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы в теории нелинейных колебаний. М.: Наука, 1974. 503 с.
- Моисеев Н.Н. Асимптотические методы нелинейной механики. М.: Наука, 1981. 379 с.
- Бердников А.С. Управление транспортировкой заряженных частиц высокочастотными электрическими полями с квазидискретным спектром. Дис. … д-ра физ.-мат. наук по спец. 01.04.01. Санкт-Петербург: Институт аналитического приборостроения РАН, 2013. 294 с.
- Мэтьюз Дж., Уокер Р. Математические методы физики. М.: Атомиздат, 1972. 397 с.
- Голиков Ю.К., Чепарухин В.В. Задача Коши для однородных гармонических потенциалов нулевой кратности//Сб. "Новые методы расчета ЭОС". Наука, 1983. С. 166-168.
- Голиков Ю.К., Краснова Н.К. Электрические поля, однородные по Эйлеру, для электронной спектрографии//Журнал технической физики. 2011. Т. 81, № 2. С. 9-15.
- Голиков Ю.К., Краснова Н.К., Абраменок О.А. Электрические спектрографы потоков заряженных частиц с потенциалами эйлерова типа//Прикладная физика. 2011. № 5. С. 69-73.
- Голиков Ю.К., Краснова Н.К. Аналитические структуры электрических обобщенно-однородных спектрографических сред//Научное приборостроение. 2014. Т. 24, № 1. С. 50-58.
- Уитеккер Э.Т., Ватсон Дж. Курс современного анализа. Часть 2: Трансцендентные функции. М.: ГИФМЛ, 1963. 516 с.
- Арцимович Л.А., Лукьянов С.Ю. Движение заряженных частиц в электрических и магнитных полях. 2-е изд. М.: Наука, 1978. 224 с.
- Список трудов проф. Ю.К. Голикова. URL: (http://iairas.ru/labs/mass_spectr_golikov_mem.pdf).
- Программа для символьных вычислений Wolfram Mathematica. URL: (http://www.wolfram.com).
- Свободно распространяемая программа для редактирования изображений Paint.NET. URL: (http://www.getpaint.net).


