Древесный (арболитовый) бетон для несущих пролетных строений

Применение легких бетонов в несущих конструкциях – широко известное и перспективное направление повышения эффективности строительных, особенно пролетных, конструкций, что обеспечивается преимущественно за счет уменьшения собственного веса конструкций [1]-[2]. Достаточное количество исследований посвящено применению легких бетонов: керамзитобетона, пенобетона, полистиролбетона и газобетона в несущих конструкциях [3]-[4]. Вместе с тем, арболит – легкий бетон с дисперсно-армированной структурой, обладая определенными преимуществами для применения в пролетных конструкциях остается рядовым стеновым материалом.

Согласно российскому государственному стандарту [5] арболит это легкий бетон на цементном вяжущем, древесной дробленке и химических добавках. При этом арболит подразделяется по видам структуры: плотной структуры, поризованной структуры, крупнопористой структуры.

На рынке строительных материалов арболит представлен исключительно стеновыми изделиями: блоками и панелями. С целью обеспечения высоких теплотехнических свойств в стеновых изделиях применяется арболит с крупнопористой или поризованной структурой. В то же время, легкие конструкционно-теплоизоляционные бетоны, особенно пенобетон и полистиролбетон, стали все более широко применяться в малопролетных изделиях, таких как перемычки, небольшие балки и плиты [6]-[7]. Основным недостатком этих изделий является низкая несущая способность: не более 1 т/пог. м. Широкой практики применения арболита в этом направлении, кроме комбинирования с тяжелым бетоном, не существует.

Вместе с тем, в сравнении с альтернативными легкими бетонами арболит обладает серьезным преимуществом, заключающимся в его дисперсно-армированной структуре, обеспечивающей повышенную прочность при растяжении. Дисперсное армирование обеспечивается древесной дробленой щепой длиной до 30 мм и поперечными размерами до 10 мм, являющейся прочной волокнистой дисперсной арматурой. Если прочность при растяжении рядовых тяжелых и легких бетонов составляет 5-10% от прочности при сжатии, то для арболита 25-30% при осевом растяжении, а при изгибе и того больше. [8]-[11]

Это рождает предположение о перспективности применения арболита в пролетных конструкциях и его большей эффективности в этом направлении по сравнению с другими легкими бетонами. Однако, работа армированного арболита в пролетных конструкциях, несмотря на некоторое количество исследований [12]-[15] мало изучена, также, как и механические и деформативные свойства арболита плотной структуры, особенно при плотности свыше D800. В связи с этим и методы расчета арболитовых конструкций опираются на классический расчет железобетонных балок и плит [16]-[17] при отсутствии данных о точности таких расчетов, что сильно ограничивает применение арболита в выбранном направлении. Существующие рекомендации в области пролетных конструкций из арболита ограничиваются техническими решениями комбинированных балок и плит из арболита и тяжелого железобетона [16], что нивелирует использование главных преимуществ арболита: низкой плотности в сочетании с повышенной прочностью при растяжении.

В связи с этим, целью настоящей работы является исследование механических и деформативных свойств арболита и армированных арболитовых балок при растяжении и изгибе с апробацией расчета разрушающего изгибного момента на основе полученных экспериментальных данных.

Для достижения цели решались следующие задачи:

• 1.    Исследование и оценка упругих свойств компонентов и структуры арболита.

• 2.    Исследование деформаций армированных арболитовых балок при изгибе, арматуры в растянутой зоне и бетона в сжатой зоне при применении композитной и стальной арматуры.

• 3.    Выполнение расчета изгибного момента армированных арболитовых балок, сравнение с фактическими данными и разработка уточненной модели расчета.

• 2    Materials and Methods

  Испытания щепы на трехточечный изгиб проводились на испытательной машине Tinius Olsen h100ku (Tinius Olsen GmbH, Goethestr.7b, 86161 Augsburg, Германия). По данным производителя для машины Tinius Olsen h100ku точность нагрузки составляла ± 0.5% в диапазоне 0.2–100% от установленного датчика силы (100 кН). Разрешение измерения перемещения траверсы составляло 0.1 мм с погрешностью до 0.01 мм. Для исключения влияния податливости траверсы испытательной машины смещение центральной точки образца под нагрузкой дополнительно контролировалось механическим индикатором часового типа, установленным под малогабаритной испытательной камерой. Разница показаний перемещений по траверсе и индикатору часового типа не превышала 2%. Испытания проводились в соответствии с [18] экспериментальные значения модуля упругости при изгибе образцов определялись при скорости нагружения 2 мм/мин.

Рис. 1. Схема испытания модуля упругости щепы при изгибе

Fig. 1 - Testing scheme of bending MoE of wood chips

В исследовании свойств арболитовых образцов и модельных конструкций с целью сравнительного анализа применялся арболит крупнопористой (D700) и плотной структуры (D900-D1300) (рис. 2).

a)

b)

Рис. 2. Макроструктура арболита: a) крупнопористой структуры; b) плотной структуры.

Fig. 2 – Macrostructure of arbolit: a) big pore structure; b) dense compact structure.

Для проведения испытаний арболита использовались стандартные образцы-кубы 10х10х10 см, образцы-балки 10х10х10х40 см и армированные образцы балки 8х12х180 см из арболита с марками по средней плотности от D700 до D1300, классом прочности от В1.5 до В5. Составы арболитовых смесей приведены в табл. 1.

Таблица 1. Составы арболитовых смесей Table 1. Arbolit concrete mixes proportions

Материалы	Составы арболитовых смесей, кг/м3
	D700	D900	D1200	D1300
	1	2	3	4
Портландцемент ЦЕМ I 52.5Б ГОСТ 31108-2020 (Аккерман, г. Новотроицк, Россия)	315	340	324	225

Древесная щепа по ГОСТ 19222-2019 (ООО «СКМ», г. Челябинск, Россия)	385	424	245	175
Песок кварцевый ГОСТ 8736-2014 (ООО Хлебороб, Челябинская область, пос. Лазурный, Россия)	―	―	615	850
Песок перлитовый ВПР М75 ГОСТ 10832-2009 (ООО Альтернатива, г. Кыштым, Россия)	―	40	―	―
Доля цементного камня в объеме арболита	0.18	0.19	0.18	0.14
Доля щепы в обьеме арболита	0.26	0.28	0.16	0.13
Доля заполнителя в объеме арболита	-	0.40	0.25	0.34
Доля пор в объеме арболита	0.66	0.13	0.41	0.39

Прочность при сжатии и изгибе определялись по российскому государственному стандарту ГОСТ 10180–2012 [19]. Модуль упругости арболита с плотностью до D800 определялся в соответствии с классом прочности по российскому государственному стандарту ГОСТ 19222-2019 [5]. Модуль упругости арболитового бетона определялся по российскому государственному стандарту ГОСТ 24452-80 [20].

Модуль упругости при изгибе определялся путем испытания стандартных образцов-балок 10х10х40 см из арболита при трехточечном изгибе с фиксацией прогиба в центре пролета (рис. 3).

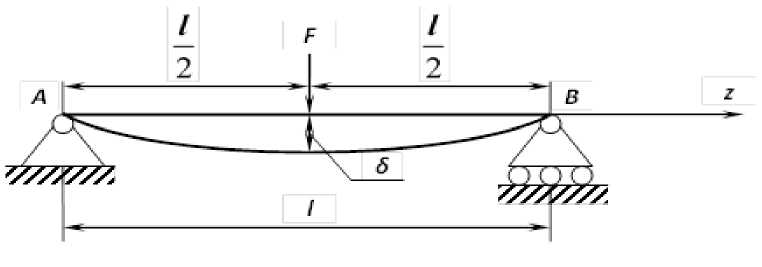
Рис. 3. Схема испытания арболита на растяжение при изгибе

Fig. 3. – Scheme of bending tensile of arbolit samples

Расчет модуля упругости при изгибе проводился по формуле

E =

Fl ³

4 bh 5'

F - нагрузка, кН; l - база, см; b - толщина сечения, см; h - высота сечения, см; 5 - прогиб, см.

Прочность и модуль упругости при осевом растяжении определялась с помощью пресса Tinius Olsen на механически обработанных образцах для сужения центрального сечения (рис. 4).

Растяжение передавалось на образец через приклеенные полимерным клеем к граням образца шарнирные пластины.

Рис. 4. Испытание арболита на осевое растяжение

Fig. 4 – Tensile of arbolit samples

Для армирования применялась композитная арматура диаметром 8, 10 мм по ГОСТ 319382012. И стальная арматура А500с по ГОСТ 5781-82. Испытания модельных армированных балок при 4-точечном изгибе проводились в соответствии со схемой, приведенной на рис. 5.

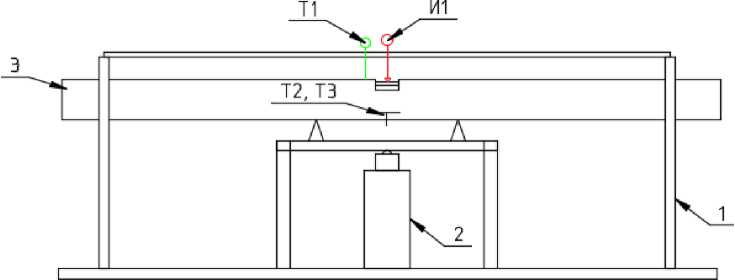
b)

Рис. 5. Схема a) и фото стенда b) испытания модельных балок при изгибе. 1 - установка; 2-домкрат; 3- образец-балка

Fig. 5 - Testing scheme a) and photo b) of beams under bending tests. 1 – stand; 2 – jack; 3 -sample-beam.

Нагружение балок осуществлялось с помощью домкрата ступенями по 50…100 кг в зависимости от класса арболита. В процессе нагружения на каждой ступени определялись следующие перемещения: прогиб балки, деформация сжатия бетона в сжатой зоне, удлинение арматуры в растянутой зоне. Также фиксировались предел трещинообразования и разрушающая нагрузка на балку.

• 3    Results and Discussion

  • 3.1    Исследование и оценка упругих свойств компонентов и структуры арболита

С целью выявления влияния структурных особенностей арболита на его деформативные свойства был проведен эксперимент по определению модуля упругости древесной щепы при изгибе. Модуль упругости щепы определялся вдоль и поперек волокон во влажном и высушенном состоянии. Также изготавливалась композитная щепа, полученная путем окунания щепы в цементное тесто и выдерживания в течение 7 сут в нормальных влажных условиях, модуль упругости которой определялся тем же методом. Результаты испытаний приведены в табл. 2.

Таблица 2. Модуль упругости древесной щепы при изгибе

Table 2. Modulus of elasticity of wood chips under bending

Средний модуль упругости при изгибе, МПа
Вдоль волокон		Поперек волокон		Цементированная
влажная	высушенная	влажная	высушенная
950	1310	770	960	2080

Результаты испытаний модуля упругости щепы предсказуемо показали, что модуль упругости при изгибе вдоль волокон выше, чем поперек волокон, и в высушенном состоянии выше, чем во влажном. Неожиданным является то, что модуль упругости щепы в обычном состоянии на порядок ниже модуля упругости древесины (14 000 МПа). Вместе с тем, щепа в омоноличенном состоянии демонстрирует многократное увеличение модуля.

Таким образом, древесная щепа в свободном состоянии вследствие частичного разрушения первоначальной структуры при дроблении обладает пониженной упругостью по сравнению с материнской древесиной. В омоноличенном матрицей обжатом состоянии щепа проявляет под изгибным моментом значительные упругие свойства при растяжении аналогично работе любых видов арматуры. Поэтому щепа является армирующим компонентом в структуре арболита и с повышением прочности и плотности растворной части эффективность ее работы должна расти. Если в свободном состоянии модуль упругости щепы близок к значениям модуля упругости матричного раствора, то в составе арболитового бетона, щепа демонстрирует значения модуля, значительно превышающие значения матричного раствора. Следовательно содержание растворной части будет решающим образом отражаться на упругих свойствах арболита. Согласно данных российского стандарта ГОСТ 19222-2019 [5] так и происходит: при повышении плотности арболита от D400 до D800 модуль упругости возрастает от 250 до 2300 МПа. Однако в этом диапазоне физико-механических свойств, упругости арболита недостаточно для получения эффективных пролетных конструкций, а развитие данной тенденции свыше D800 не подкреплено иследованиями.

В дальнейшем исследовании проводились испытания модуля упругости арболита составов различной плотности, приведенных в табл. 1. Зависимость “напряжение-деформация” при сжатии показывает, что арболит является упругим материалом независимо от плотности (рис. 6). Такой же характер сохраняется и при растяжении. Очевидно, упругие свойства арболита задаются упругими свойствами древесной щепы.

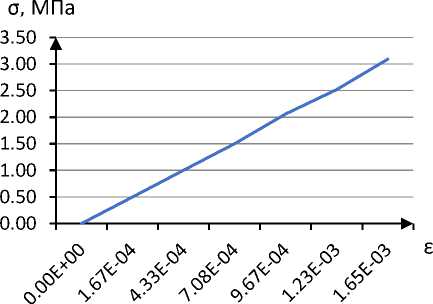
a)

σ, МПа

4.50 1

4.00

3.50

3.00

2.50

2.00

1.50

1.00

0.50

0.00

. ^ , s^ лХ/ аХ/ Л

^ s^ ^ε

^ _О^ ^ ^ о^ V V 'Ъ-   ^

У ^■ <У

b)

Рис. 6. Зависимость “напряжение-деформация” арболита при сжатии, а – D900, б – D1200

Fig. 6 – Stress-strain curve of arbolit under compression, а – D900, б – D1200

В табл. 3 приведены результаты испытаний прочности и модуля упругости при сжатии (призменной), изгибе, осевом растяжении арболита заданных составов.

Таблица 3. Модуль упругости и прочность при сжатии и растяжении арболита

Table 3. Compressive and tensile modulus of elasticity and strength of arbolit

Наименование показателя	Составы арболитовых смесей
	D700	D900	D1200	D1300
	1	2	3	4
Призменная прочность при сжатии, МПа	1.5	3.8	6.0	6.6
Прочность при изгибе, МПа	2.0	4.4	6.5	7.0
Прочность при осевом растяжении, МПа	0.31	0.68	1.35	1.42
Модуль упругости при сжатии, МПа	700	2700	5900	6600
Модуль упругости при изгибе, МПа	1800	3600	8000	9000
Модуль упругости при осевом растяжении, МПа	1550	3500	7800	8900

Анализ данных прочности показывает:

• 1)    прочность арболита при изгибе превышает прочность при сжатии R b , значительно превышая характеристики при изгибе тяжелого бетона;

• 2)    прочность при осевом растяжении R _bt арболита всех плотностей подчиняется зависимости

R bt = ( 0.23...0.25 ) х R b ,                                        (2)

Анализ данных испытаний упругих свойств показывает:

• 1)    модули упругости арболита при изгибе и осевом растяжении близки по значению и взаимозаменяемы;

• 2)    арболит - разномодульный материал, модуль упругости при растяжении E _bt арболита значительно выше модуля упругости при сжатии E _b ;

• 3)    модуль упругости при изгибе арболита крупнопористой структуры близок к модулю упругости цементированной щепы в свободном состоянии, модуль упругости арболита может быть определен как

• 3.2    Исследование деформаций армированных арболитовых балок при изгибе, арматуры в растянутой зоне и бетона в сжатой зоне при применении композитной и стальной арматуры

E bt = k arb х E b ,                                           (3)

k_arb = 2.3 для крупнопористого арболита и 1.3 для арболита плотной структуры.

С учетом повышенной прочности и модуля упругости арболита при растяжении следует исследовать деформативные свойства армированных балок и выявить вклад арболита в несущую способность балки.

Модельные армированные балки изготавливались из составов арболитовых смесей (1, 2) D700 и D900 с армированием растянутой зоны одним стержнем стеклопластиковой арматуры диаметром 8 и 10 мм, или стальной арматуры диаметром 10 и 14 мм. При нагружении по 4точечной схеме определялись: нагрузка, растяжение оголенного участка арматуры, прогиб, деформация сжатой зоны, предел трещинообразования, разрушающая нагрузка. Напряжение в арматуре у _а рассчитывалось через модуль упругости E _s и относительную деформацию e _s арматуры под нагрузкой

° a = E s X £ _s .                                          (4)

Характеристики материалов для расчета по предельным состояниям (ПС) 1 группы и результаты испытаний приведены в табл. 4

Таблица 4. Характеристики материалов для расчета и результаты испытаний балок Table 4. Materials’ parameters and beams’ testing results

Показатели	Формула/ обозначение	Составы
		1	2	2	1	1	2	1	2
Размеры балки: длина, ширина, высота	l (база), м	1.2	1.2	1.2	1.2	1.2	1.2	1.2	1.2
	b , см	8	8	8	8	8	8	8	8
	h , см	16	16	16	16	16	16	16	16
Характеристики арболита	класс, B	1	2	2	1	1	2	1	2
	D , кг/м3	800	900	900	800	800	900	800	900
	Rb , МПа	0.6	1.2	1.2	0.6	0.6	1.2	0.6	1.2
	Eb , МПа	700	1 400	1 400	700	700	1 400	700	1 400
	R bt , МПа	0.24	0.38	0.38	0.24	0.24	0.38	0.24	0.38
Характеристики арматуры: диаметр, толщина защитного слоя, площадь, прочность при растяжении, модуль упругости	Ø, мм	АСК Ø8	АСК Ø8	АСК Ø10	АСК Ø10	А400 Ø10	А400 Ø10	А400 Ø12	А400 Ø12
	a , см	2	2	2	2	2	2	2	2
	As , см2	0.50	0.50	0.79	0.79	0.79	0.79	1.13	1.13
	Rs , МПа	1 000	1 000	1 000	1 000	355	355	355	355
	Es , МПа,103	30	30	30	30	200	200	200	200
Относительное удлинение арматуры при разрушении	ε s , 104	1.0	2.3	4.8	3.0	9.3	1.3	4.4	6.4
Разрушающая нагрузка	q , кг	160	268	360	330	450	560	550	560
Напряжение в арматуре фактическое	σ a , МПа (4)	3.00	6.94	14.25	8.97	18.57	25.00	8.89	12.73
Доля напряжения арматуры от прочности факт	k a , 103	3	7	14	9	52	70	25	36

По результатам испытаний балок сделаны следующие выводы:

• 1)    при 1-стороннем армировании растянутой зоны определяющим фактором в разрушении арболитовых балок из арболита крупнопористой структуры является прочность сжатой зоны, поскольку трещинообразование развивалось от сжатой зоны с последующим развитием и разрушением преимущественно в точке приложения нагрузки;

• 2)    арматура при нагружении деформировалась без проскальзывания, тем не менее напряжение в арматуре при нагружении составляет от 0.5 до 1.5% от прочности при растяжении композитной арматуры и от 4 до 7% прочности при растяжении стальной арматуры, что свидетельствует о релаксации напряжений вследствие низкого модуля упругости и высокой податливости арболита и делает применение композитной арматуры в подобных изделиях бесперспективным;

• 3)    решающим фактором в росте напряжения в арматуре при нагружении балки является модуль упругости арболита, повышение модуля упругости в два раза обеспечивает увеличение доли напряжения в арматуре в 3-4 раза.

• 3.3    Апробация расчета изгибающего момента армированных арболитовых балок

Выполнение расчета момента балок с 1-сторонним армированием по классической схеме, исходя из равенства напряжений в растянутой и сжатой зонах, в связи с низкими показателями прочности сжатой зоны и низким уровнем вовлеченности арматуры в работу, изначально представлялось и в последствии оказалось неосуществимым. При расчете сжатой зоны по модели x =

R s X A s ^Rb ^{X b}

сжатая зона приобретает значения, превышающие высоту изделия.

При расчете с учетом фактических деформаций арматуры и бетона величина сжатой зоны рассчитывается адекватно. Относительная высота сжатой зоны определялась по [17, 21]

^ b 2

E b

R b

.

^ r =

0.8

,

1 + *'

^ b 2

Тогда высота сжатой зоны x = ^r X hо. (7)

В табл. 5 приведены показатели фактического и результаты расчета (с формулами) изгибающего момента с учетом фактических деформаций арболита и арматуры. При расчете определялись: момент сопротивления сечения W _pl , изгибного момента сечения арболита M_bt , изгибного момента арматуры M ' , изгибного момента армированной балки M Э .

Сравнение фактических и расчетных показателей разрушающих изгибных моментов по показателям фактических деформаций бетона и арматуры демонстрирует невысокий уровень сходимости, отклонение составляет от 3 до 25%, что может быть следствием как погрешности эксперимента, так и несовершенством расчетной базы. Вместе с тем, обеспеченность расчета арболитовых балок со стальным армированием с запасом 0-25% от факта, позволяет признать выбранный метод расчета пригодным для задач предварительного расчета по первой группе ПС. Следует отметить значительный вклад (до 30%) изгибающего момента сечения арболита в общий изгибающий момент балки, что связано с повышенной прочностью арболита при растяжении и низкой долей напряжения в арматуре под нагрузкой.

Данный расчет показывает неплохие результаты только при условии применения фактических показателей удлинения арматуры под нагрузкой. Проблематикой воспроизводимости данного расчета является необходимость расчетного прогнозирования фактического напряжения в арматуре. В связи с этим, были разработаны зависимости фактического напряжения арматуры в арболите при нагружении от выявленных значимых факторов модуля упругости арматуры и бетона, а также прочности и сечения арматуры и предложен следующий алгоритм расчета арболитовых балок по 1-й группе предельных состояний (ПС).

Таблица 5. Показатели фактического и расчетного разрушающих изгибающих моментов

Table 5. Fact and design bending moments

Показатель	Формула	Составы-арматура
		1-АСК Ø8	2-АСК Ø8	2-АСК Ø10	1-АСК Ø10	1-А400 Ø10	2-А400 Ø10	1-А400 Ø12	2-А400 Ø12
Относительн ая высота сжатой зоны (для стальной арматуры)	^ г (6)	0.63	0.55	0.45	0.52	0.72	0.70	0.76	0.74
	x (7)	8.78	7.72	6.31	7.26	10.11	9.77	10.65	10.43

Высота сжатой зоны, см h0 = b - a 14 14 14 14 14 14 14 14 Изгибающий момент арболита, кгс∙см Mbt = Wpi x Rbt 1545 2446 2446 1545 1545 2446 1545 2446 Момент сопротивлен ия сечения арболита, см3 2 Mn, = 1.1x b x--- pl             3.5 644 644 644 644 644 644 644 644 Изгибающий момент конструктивн ой арматуры, кгс∙см /' = Rb xbxxx^h0 -x) 4049 7514 6566 3615 4340 8551 4434 8795 Расчетный изгибающий момент балки, кгс∙см M Э = Mbt + M' 5594 9960 9012 5160 5885 10997 5979 11241 Фактический изгибающий момент балки, кгс∙см M _ q x l факт    6 3200 5360 7200 6600 9000 11200 11000 11200 Расчет напряжения в арматуре арболитовой балки под изгибной нагрузкой предлагается выполнять по следующей авторской модели ■    ka х Rs as a Es- x A                                         (8) s Eb ka =0.3 для стеклопластиковой арматуры;

• k_a =6 для стальной арматуры.

В табл. 6 приведены результаты расчета разрушающего момента балки с применением разработанных моделей. Как видно, модель демонстрирует даже несколько большую сходимость по сравнению с расчетом по фактическим деформациям, при этом обеспеченность запаса при расчете балок со стальным армированием сохраняется.

Таблица 6. Расчет изгибающих моментов с применением моделей напряжения в арматуре Table 6. Calculation of bending moment using reinforcement’s stress model

Показатель	Формула	Составы №№ по табл. 1 / арматура
		1-АСК Ø8	2-АСК Ø8	2-АСК Ø10	1-АСК Ø10	1-А400 Ø10	2-А400 Ø10	1-А400 Ø12	2-А400 Ø12
Напряжение в арматуре расчетное, МПа	(8)	37.33	74.67	47.26	23.63	9.44	18.87	6.60	13.19
Расчетная высота сжатой зоны, см	x ' = ^ r x h 0	4.57	2.87	3.95	5.84	10.62	10.09	10.78	10.40
	C T ,    0.8     Es = 5 ,    =   F         Es 1    + E^- E b 2	0.33	0.20	0.28	0.42	0.76	0.72	0.77	0.74
Расчетный изгибающий момент конструктивн ой арматуры, кгс∙см	M' = Rb x b x x x^ h 0 - x j	2569	3461	4557	3105	4429	8674	4456	8786

Расчетный изгибающий момент балки, кгс∙см	Mp = Mbt + M'	4114	5907	7003	4649	5974	11120	6001	11232
Фактический изгибающий момент балки, кгс∙см	q x i M.1,  = — факт    6	3200	5360	7200	6600	9000	11200	11000	11200

В целом, основным выводом из рассмотренной серии испытаний является то, что для получения несущих арболитовых балочных конструкций необходимо:

• 1)    армирование сжатой зоны арболита, т.е. армирование арболитовых балок стальными каркасами;

• 2)    повышение модуля упругости арболита при сжатии путем оптимального повышения плотности структуры арболита с целью повышения доли напряжения арматуры под нагрузкой.

Для проверки тезиса и апробации расчета изгибающего момента арболитовых балок, армированных стальными каркасами, были изготовлены арболитовые балки из арболита плотности D700, D900, D1200, D1300 (табл. 1, составы 1, 2, 3, 4). Стальные каркасы изготавливались из конструктивной арматуры А500с периодического профиля одного диаметра в верхней и нижних зонах (1 вариант – 10 мм, 2 вариант – 14 мм), соединенных хомутами из проволоки Вр-I диаметром 6 мм.

Результаты испытаний и расчета приведены в табл. 7. По результатам физико-механических испытаний сделаны следующие выводы:

• 1)    проведенные мероприятия позволили повысить несущую способность балок из арболита одного класса более чем в 3 раза;

• 2)    повышение прочности и модуля упругости арболита при одинаковом армировании приводит к значительному повышению изгибного момента балки;

• 3)    повышение диаметра арматуры каркаса приводит к повышению изгибного момента меньшему, чем прирост площади армирования.

При традиционном расчете железобетонной балки, армированной каркасом, изгибный момент бетонного сечения, как малозначительный, не учитывается и определяется исключительно свойствами арматуры по [21]:

M ult = R S ^X A S ^X( h 0 - a ' ) .                                       (9)

По факту ни зависимость от площади сечения, ни малозначимость фактора изгибного момента арболита в сечении не подтверждаются. Это связано с тем, что доля напряжения в арматуре зависит от модуля упругости арболита, а изгибной момент сечения арболита соизмерим с конструктивным моментом арматуры: прочность при растяжении арболита класса В5 превышает прочность при растяжении тяжелого бетона класса B30.

В связи с этим, авторами предлагается метод расчета, определяющий разрушающий изгибный момент балки как сумму моментов сечения арболита и арматуры:

^Mp = ^Mbt + ^M ' .                                   (10)

При этом изгибной момент конструктивной арматуры предлагается определять с учетом расчетной доли напряжения арматуры по следующей авторской модели

M ' = k_a x R S x A S x ( h 0 - a ' ) ,                                   (11)

0.05 x E_b

Таблица 7. Расчет изгибающих моментов арболитовых балок, армированных каркасами

Table 7. Calculation of bending moment of arbolit beams reinforced by carcasses

Параметры	Формула или обозначение	Составы №№ по табл. 1
		2	2	3	3	4	4	1
Размеры балки	l (база), м	1.2	1.2	1.2	1.2	1.2	1.2	1.2

	b , см	8	8	8	8	8	8	8
	h , см	16	16	16	16	16	16	16
Характеристики арболита	класс, B	3.5	3.5	7.5	7.5	7.5	7.5	2.5
	D , кг/м3	900	900	1200	1200	1300	1300	800
	Rb , МПа	2.5	2.5	5	5	5	5	1.5
	Eb , МПа	2700	2700	5900	5900	6600	6600	1 700
	Rbt , МПа	0.68	0.68	1.35	1.35	1.35	1.35	0.41
Характеристики арматуры	Ø, мм	А400 Ø10	А400 Ø14	А400 Ø10	А400 Ø14	А400 Ø10	А400 Ø14	А400 Ø10
	a ' , см	3.5	3.5	3.5	3.5	3.5	3.5	3.5
	A S ' , см2	0.79	1.54	0.79	1.54	0.79	1.54	0.79
	R S ' , МПа	355	355	355	355	355	355	355
	E S ' , МПа	200 000	200 000	200 000	200 000	200 000	200 000	200 000
Разрушающая нагрузка	q , кг	667	480	1 013	1 280	1 333	1 707	600
Изгибающий момент арболита	Мы = W pi х R b , кгс∙см	4345	4345	8689	8689	8689	8689	2607
	2 W, = 1.1 х b х — pl             3.5	644	644	644	644	644	644	644
Доля напряжения в арматуре расчетная	k = 0.5 х Eb a = 1000	0.135	0.135	0.295	0.295	0.330	0.330	0.085
Изгибающий момент конструктивной арматуры	M' = k х R „ х A„ х aSS х ( h 0 - a ') ,кгс∙см	3407	6642	7446	14515	8329	16237	2145
	h 0 , см	12.5	12.5	12.5	12.5	12.5	12.5	12.5
Изгибающий момент балки расчетный	M p = M bt + M' , кгс∙см	7752	10987	16135	23204	17019	24926	4752
Изгибающий момент фактический	q х i M = , факт    6 кгс∙см	13340	9600	20260	25600	26660	34140	12000

Сравнение результатов расчета с экспериментальными данными показывает удовлетворительную сходимость, средний коэффициент вариации модели не превышает 15%. Поэтому предложенную модель расчета арболитовых балок по первой группе ПС, армированных стальными каркасами, можно признать действительной.

• 4 Conclusions

Выполнено исследование механических и деформативных свойств арболита и армированных арболитовых балок при растяжении и изгибе с апробацией расчета разрушающего изгибного момента на основе полученных экспериментальных данных. Результаты работы позволяют заложить основу расчета и изготовления несущих балочных конструкций из арболита:

• 1.    Исследование и оценка упругих свойств компонентов и структуры арболита показало, что арболит является упругим материалом, упругость которого обеспечивается упругими свойствами цементированной древесной щепы. Дисперсно-армированная структура обеспечивает арболиту повышенные, по сравнению с другими легкими и тяжелыми бетонами, прочность и модуль упругости при растяжении. Прочность арболита на растяжение при изгибе превышает прочность при сжатии. Поэтому изгибный момент сечения арболита вносит вклад в общий изгибный момент балки, соизмеримый с изгибным моментом арматуры в ее составе.

• 2.    Исследование деформаций армированных арболитовых балок показало, что при удовлетворительном сцеплении арболита со всеми видами арматуры вследствие низкого модуля упругости при сжатии, доля напряжения арматуры при плотности арболита до D900 не превышает 10% от прочности арматуры при растяжении. Помимо этого, в связи с низкими механическими и деформативными свойствами арболита в сжатой зоне эффективным является армирование сжатой зоны, т.е. армирование арболитовых балок каркасами. Вместе с тем, повышение модуля упругости арболита приводит к непропорциональному увеличению доли напряжения арматуры.

• 3.    Разработаны модели оценки доли напряжения в арматуре арболитовой балки под изгибной нагрузкой при 1-стороннем и каркасном армировании. Факторами модели являются модули упругости арматуры и арболита. Апробация расчета по первой группе ПС разрушающего изгибного момента армированных арболитовых балок привела к уточнению расчета балок и с односторонним, и с каркасным армированием. Уточнение заключается:

• -    в расчете по разработанной авторской модели доли напряжения арматуры под нагрузкой и учете доли напряжения при расчете сжатой зоны арболитовой балки;

• -    в обязательном учете изгибного момента сечения арболита в расчете общего разрушающего изгибного моменте арболитовой балки.

5 Fundings

Исследование выполнено за счет гранта Российского научного фонда № 23-29-00425,