Дробный орбитальный угловой момент Гауссова пучка с внедренным внеосевым оптическим вихрем

В [1, 2] А. Цайлингер предложил формировать пару фотонов (в ходе спонтанного параметрического рассеяния) в перепутанном состоянии по орбитальному угловому моменту (ОУМ) с помощью смещения центров Гауссова пучка и голограммы «с вилочкой», которая формирует оптические вихри. Он предположил, что при малом смещении между центрами формируется линейная комбинация Гауссова пучка и пучка Лагер-ра–Гаусса. В [3] также экспериментально показали, что можно формировать перепутанные по ОУМ стоксовый и антистоксовый фотоны с помощью четырехволнового смешения в ансамбле «горячих» атомов и при смещении центров Гауссова пучка и голограммы «с вилочкой». Известны также исследования трансформации оптических вихрей и в классическом свете. Под оптическим вихрем здесь понимается лазерный пучок с изолированным нулем интенсивности на оптической оси и спиральной фазой с целым топологическим зарядом. В [4] теоретически изучается влияние на оптический вихрь смещения вдоль оптической оси центра перетяжки Гауссова пучка от плоскости спиральной фазовой пластинки, совмещенной с дифракционной линзой (спиральная линза). В [5] экспериментально исследуется прохождение оптического вихря через набор малых отверстий в непрозрачном экране, центры которых лежат на окружности. Показано, что при этом вырожденный оптический вихрь n -го порядка распадается на n невырожденных оптических вихрей (1-го порядка). В [6] исследуется трансформация оптического вихря с помощью внесения в него разной степени эллиптичности. Эта работа [6] продолжает более ранние работы по исследованию эллиптических оптических вихрей [7, 8]. В [9] предложено формировать оптический вихрь с помощью набора малых отверстий в не-

прозрачном экране, центры которых расположены на спирали. Небольшие деформации направляющей спирали приводят к искажению формы оптического вихря.

Наиболее близкими по тематике к данной работе являются ранние статьи авторов [10– 12]. В них рассматриваются теоретически и экспериментально трансформации оптического вихря, которые получаются в результате комплексного смещения исходной функции комплексной амплитуды в декартовой системе координат. Такое смещение приводит к асимметрии оптического вихря: вместо светового кольца (или «пончика») формируется полумесяц. В [10] комплексное смещение координат применено для пучков Бесселя, а в [11] – для пучков Лагерра–Гаусса. В [12] оптический вихрь n -го порядка преобразуется в n оптических вихрей 1-го порядка с помощью использования эллиптического Гауссова пучка, падающего на спиральную фазовую пластинку.

В данной работе теоретически и экспериментально изучается трансформация оптического вихря, предложенная в [1, 2], когда на амплитудную голограмму «с вилочкой» падает Гауссов пучок, центр перетяжки которого смещен в поперечной плоскости от центра «вилочки». Заметим, что в [1, 2] нет теории такого преобразования. В данной работе оптический вихрь, возникающий из-за смещения центров Гауссова пучка и голограммы «с вилочкой» (или центра спиральной фазовой пластинки), называется асимметричным Гауссовым оптическим вихрем (АГВ). Получено аналитическое выражение для ОУМ таких пучков и показано, что ОУМ таких пучков дробный, то есть световое поле представляет собой линейную комбинацию счетного набора оптических вихрей с целым топологическим зарядом. Если в таком состоянии будут находиться два фотона, то это состояние будет перепутанным по ОУМ. Заметим, что при ком- плексном смещении координат ОУМ пучков Бесселя [10] и Лагерра–Гаусса [11] растет. Растет также ОУМ у эллиптического вихревого пучка Эрмита–Гаусса [12]. В отличие от них ОУМ асимметричного Гауссова вихря, описанного в данной работе, убывает с увеличением расстояния между центрами Гауссова пучка и спиральной фазовой пластинки.

1. Амплитуда Гауссова оптического вихря

Рассмотрим Гауссов пучок с амплитудой в пере-

тяжке в виде

E о ( x , y ) = exp ( - ( x ² + y ² )/ w ² ) ,                   (1)

где ( x , y ) – декартовы координаты, w – радиус перетяжки. Пусть в пучок (1) внедрен оптический вихрь с топологическим зарядом n , смещенный на расстояние x 0 по оси x от центра Гауссова пучка. Амплитуда та-

кого оптического вихря описывается выражением:

A n ( ^x, y ) = [ ( ( ^{x - x} 0 ) ⁺ iy ) / ^w ] •                      ⁽²⁾

Функцию пропускания (2) можно реализовать с помощью амплитудной голограммы «c вилочкой» [13]. Тогда с помощью преобразования Френеля можно получить амплитуду АГВ на расстоянии z от начальной плоскости (плоскости перетяжки Гауссова пучка) в цилиндрических координатах:

E n ( r , Ф, z ) = w ^- n [ q ( z ) ] ⁽ n ^{+ 1 ) [} re" " - q ( z ) x о ] n ^x

x exp

r ² + ikr² w ² ( z )   2 R ( z )

где k – волновое число света, w2 (z) = w2 (1 + z2 /z 02),

R ( z ) = z ( 1 + z 0² / z ² ) ,                                    (4)

q (z ) = 1 + iz /z о, где z0 = kw2/2 – расстояние Рэлея.

Из (3) видно, что амплитуда АГВ описывается двумя сомножителями, последний из которых представляет собой радиально-симметричный Гауссов пучок на расстоянии z от перетяжки с радиусом пучка w ( z ) и радиусом кривизны волнового фронта R ( z ). Сомножитель в (3), отвечающий за асимметрию пучка, выпишем отдельно:

F = ( re ^{ф -} q ⁽ z ) x о ) n =

= [ ( r cos ф - x ₀ ) + i ( r sin ф - zx 0 / z ₀ ) ] n .

Распределение интенсивности поля (3) будет пропорционально квадрату модуля величины (5) и будет иметь вид:

I = E ( ^r , ф > ^z )|² = w~^{2 n} \q ( ^z )|^{2 (} n ^{+ 1 )} exp

2 r ²

^{w 2} ( ^z )

2                            Я ”

r ² + q ( z ) x 0 - 2 rx ₀ ( cos ф + ( z / z ₀)sin ф ) I .

Из (6) видно, что при z =0 сомножитель (5) имеет

вид

|F |² = [ r ² + x 0 - 2 rx ₀cos ф] .                      (7)

Выражение (7) вместе с Гауссовой экспонентой из (6) описывает неоднородное кольцо в виде полумесяца, у которого в точке x = x 0 имеется изолированный нуль интенсивности n -го порядка. При x 0 >0 полумесяц расположен так, что максимальная интенсивность на нём (при фиксированном радиусе r ) достигается при ф = п , а минимальная - при ф = 0 (и наоборот при x 0 <0). На расстоянии от перетяжки, равном расстоянию Рэлея z = z 0 , вместо (7) получим для сомножителя (5), отвечающего за асимметрию пучка, следующее выражение:

|F |² = [ r ² + 2 x 2 - 2V2 rx ₀cos ( ф-л/ 4 ) ] .         (8)

Из (8) следует, что на расстоянии z = z 0 полумесяц повернулся на 45° против часовой стрелки. Максимум интенсивности на полумесяце лежит на луче под углом ф = 5 п / 4, а минимум - на луче под углом ф = л / 4. При удалении на большое расстояние z >>  z 0 от перетяжки вместо (8) получим:

I F |² = [ r ² + ( zx ₀/ z ₀ ) 2 - 2( zx ₀/ z ₀) r sin ф] .           (9)

Из (9) видно, что в дальней зоне ( z >>  z 0 ) дифракции полумесяц поворачивается на 90° против часовой стрелки, и максимум интенсивности лежит на луче ф = 3 л / 2, а минимум интенсивности - на луче ф = л / 2.

Из (5) прямо следует, что изолированный нуль интенсивности АГВ имеет координаты:

[ x = x _n,

0        ⁰ ,                                                     (10)

[ y = x 0 ( z / z 0 ).

То есть изолированный нуль, лежащий в начальной плоскости на горизонтальной оси в точке x = x 0 , при увеличении расстояния z движется перпендикулярно горизонтальной оси на бесконечность.

2. Дробный орбитальный угловой момент АГВ

В [1 –3] экспериментально было продемонстрировано, что смещение центра Гауссова пучка относительно центра оптического вихря приводит к формированию перепутанных по орбитальному угловому моменту фотонов, то есть у АГВ должен быть дробный ОУМ. Покажем, что это действительно так. Так как при распространении лазерного пучка его ОУМ сохраняется, можно рассчитывать его в любой плоскости, например, в плоскости перетяжки. Можно показать, что энергия W n АГВ (3) и проекция ОУМ J nz на ось z будут равны:

^ 2 ^

W n = ff E n ( r ,Ф, z = 0 )|² rdrd Ф = 00

= ( n w ²/2 ) ( x 0 / w ) ² n ]n ;( c n ) ² 1 ! ( w /72 x 0 ) ^{2 1} =       (11)

1 = 0

= ( n w 2 /2 ) 2 ^- n n ! L n ( - ^ ² ) ,

Г . ^{2 п}_ _d E

^J"--⁼ Im if f ^E n    "rdrd Ф

I 0 0     дФ n                                   2l

= n ( n w ²/2 ) ( x 0 / w ) ^{2 n} 1 се j / ! ( w /72 x о ) =     (12)

l = 1

= n (nw 2/2) 2 - nn! Ln-1 (Ч2), где с- = n !/l !/(n -1)! - биномиальные коэффициенты, Ln (...) - полиномы Лагерра и ^ = 2X0x 0 /w. Из (11), (12) следует, что нормированный ОУМ асимметричного Гауссова вихря (3) будет равен:

J n

W n

n

1 c - c -* ^-2 l    L n J- s ²)

----------------= n----;----f .

1 ( c n ) ² / !, ^{- 2 1}       L n H ² )

l = 0

Из (13) видно, что нормированный ОУМ АГВ в общем случае дробный. При x 0 =0 из (13) следует хорошо известный результат, что ОУМ моды Лагерра– Гаусса [14] равен топологическому заряду n :

j -- / W n = n .

Из (13) найдем более простые выражения для n = 1 и n =2, из которых можно сделать конкретные выводы о поведении ОУМ АГВ . Например, при n = 1 из (13) получим:

1 + ( 42x ₀/ w ) . (15)

J 1 - / W 1 = 1

Это выражение совпадает с полученным ранее в [15]. Из (15) следует, что при отсутствии смещения x 0 =0 ОУМ равен 1, при смещении центра оптического вихря от центра Гауссова пучка на расстояние x ₀ = w / V2 ОУМ пучка будет равен 1/2, а при большом смещении x 0 →∞ ОУМ стремится к нулю. Физически это понятно, так как оптический вихрь при достаточном удалении уже не принадлежит Гауссову пучку, а находится в области пространства, где нет световой энергии. При n =2 из (13) получим:

J 2 - / W 2 = 4 ( 1 + ^ 2 )/( 2 + ⁴ ^ 2 +^ 4 ) . (16)

Из (16) следует, что при отсутствии смещения x 0 = 0 ( ^ = 0) ОУМ равен 2, при x ₀ = w / V2 ( ^ = 1) ОУМ равен 8/7, а при большом смещении x 0 →∞ ( ^ ^^) ОУМ близок к нулю. Из (13) следует, что для любого топологического заряда n при x 0 → ∞ нормированный ОУМ убывает c x 0 квадратично.

Выше мы рассмотрели асимметричные Гауссовы оптические вихри, которые экспериментально можно реализовать при дифракции Гауссова пучка на амплитудной голограмме с характерной «вилочкой» в точке сингулярности [1, 2, 13]. Такая ситуация будет описываться уравнениями (1)–(3). Однако амплитудная голограмма с «вилочками» имеет невысокую эффективность (несколько процентов). Для увеличения эффективности при формировании АГВ ниже в эксперименте будет использована другая оптическая схема, когда Гауссов пучок падает на спиральную фазовую пластинку (СФП), реализованную с помощью жидкокристаллического микродисплея . Такую экспериментальную схему также можно описать аналитически (Приложение), хотя формулы получаются более громоздкие .

3. Экспериментальное формирование АГВ

На рис. 1 показана экспериментальная схема. Излучение из твердотельного лазера с длиной волны 1 = 532 нм направлялось через пинхол PH и линзу L 1 на дисплей пространственного модулятора света SLM, на котором была выведена фазовая функция СФП заданного порядка. Отражённый от модулятора пучок подвергался пространственной фильтрации с помощью системы линз L 2 и L 3 , а также диафрагмы D . Далее отфильтрованный лазерный пучок направлялся на линзу L 4 , которая фокусировала его на матрицу CMOS-камеры. Для получения интерферограмм в схему были добавлены светоделительные кубики BS 1 и BS 2 . Первый из них делил исходный пучок на два, один из которых направлялся на модулятор света, а второй оставался неизменным. Далее эти два пучка сводились в один с помощью второго светоделительного кубика, чтобы на камере можно было наблюдать картину их интерференции. Линза L 5 была использована для внесения в Гауссов пучок сферического волнового фронта. Диаметр перетяжки Гауссова пучка 2 w = 1400 мкм.

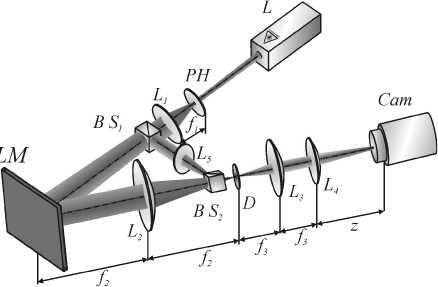
Рис. 1. Экспериментальная схема: L – твердотельный лазер ( Л = 532 нм), PH - пинхолл (40 мкм), L i , L 2 , L 3 , L 4 и L 5 - линзы с фокусными расстояниями (f 1 = 150 мм, f 2 = 350 мм, f 3 = 150 мм, f 4 = 250 мм, f 5 = 150 мм), BS 1 , BS 2 – светоделительные кубики,

SLM – пространственный модулятор света PLUTO VIS (разрешение 1920 × 1080 пикселей, размер пикселя – 8 мкм), D – диафрагма, выполняющая роль пространственного фильтра, Cam – видеокамера ToupTek U3CMOS08500KPA (размер пикселя – 1,67 мкм)

В экспериментах исследовалось влияние смещения центра освещающего Гауссова пучка относительно центра спиральной фазовой пластинки, выведенной на дисплей модулятора света. На рис. 2–6 показаны сформированные в этих случаях распределения интенсивности в фокальной плоскости линзы с фокусным расстоянием f =250 мм. Там же показаны соответствующие им интерферограммы, полученные в результате интерференции исследуемых пучков и Гауссова пучка со сферическим волновым фронтом. Размеры каждого кадра на всех рис. 2–6 составляют 750×750 мкм. Следует отметить , что из-за наличия светоделительного кубика на пути лазерного луча, отражённого от дисплея модуля- тора, фокальная плоскость линзы L2 смещается по направлению к модулятору света. Это приводит к тому, что на линзу L4 падает сходящийся лазерный пучок, поэтому картины дифракции Фраунгофера мы наблюдали на расстоянии z =230 мм от плоскости линзы L4.

На рис. 2 показаны распределения интенсивности (рис. 1 а–г ) и соответствующие им интерферограммы (рис. 1 д–з ) для оптических Гауссовых вихрей с топологическими зарядами n от 1 до 4 при отсутствии смещения между центрами СПФ и Гауссова пучка. Из рис. 2 видно, что картины оптических вихрей обладают радиальной симметрией, то есть сформированы хорошо известные картины типа «пончиков» с нулем интенсивности в центре.

совпадают (x 0 = 0). Верхний ряд – полученные распределения интенсивности для СФП с топологическим зарядом: (а) n = 1, (б) n = 2, (в) n = 3, (г) n = 4. Нижний ряд – полученные интерферограммы для СФП с топологическим зарядом: (д) n = 1, (е) n = 2, (ж) n = 3, (з) n = 4. Размеры картинок – 750×750 мкм

На рис. 3 показаны распределения интенсивности Гауссовых оптических вихрей с топологическими зарядами n от –1 до –4 при небольшом смещении центра СФП от центра Гауссова пучка (x0 = 0,25w). Из рис. 3 видно, что все «пончики» потеряли, хотя и не сильно, радиальную симметричность, а спиральные интерферограммы сменили направления «закруток» с «против часовой стрелки» на «по часовой стрелке» из-за того, что у оптических вихрей поменялся знак топологического заряда. Из рис. 3 видно, что мини- мальная интенсивность на неоднородном световом

Рис. 3. Смещение центра падающего пучка от центра СФП составляет x 0 = 0,25w. Верхний ряд – полученные распределения интенсивности для СФП с топологическим зарядом: (а) n = –1, (б) n = –2, (в) n = –3, (г) n = –4. Нижний ряд – полученные интерферограммы для АГВ с топологическим зарядом: (д) n = –1, (е) n = –2, (ж) n = –3, (з) n = –4. Размеры картинок – 750 × 750 мкм

На рис.4 показаны распределения интенсивности Гауссовых оптических вихрей с топологическими заря- дами n от 1 до 4 при большом смещении центра СФП от центра Гауссова пучка (x0 = 0,5w).

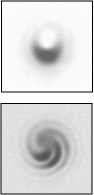
Рис. 4. Смещение центра падающего пучка от центра СФП составляет x 0 = 0,5w. Верхний ряд – полученные распределения интенсивности для СФП с топологическим зарядом: (а) n = 1, (б) n = 2, (в) n = 3, (г) n = 4. Нижний ряд – полученные интерферограммы для СФП с топологическим зарядом: (д) n = 1, (е) n = 2, (ж) n = 3, (з) n = 4. Размеры картинок – 750 × 750 мкм

Из рис.4 видно, что, во-первых, вместо «пончиков» появились «полумесяцы», и, во-вторых, из-за смены знака топологических зарядов минимальная точка интенсивности в неоднородном распределении интенсивности на кольце лежит на луче под углом 90°, в отличие от картин на рис.3, в которых минимальная интенсивность на кольце лежит на луче под углом –90°.

На рис.5 показаны распределения интенсивности Гауссовых оптических вихрей с топологическими зарядами n от 1 до 4 при еще большем смещении центра СФП от центра Гауссова пучка ( x 0 = w ). Из рис. 5 видно, что вместо кольца (рис.2) и полумесяца (рис.4) получается искаженное фокусное пятно и на интерферограммах уже нет характерных для оптических вихрей спиралей. Это означает, что изолированный нуль интенсивности, вблизи которого сосредоточена фазовая сингулярность, сместился из области света в область тени.

составляет x0 = w. Верхний ряд – полученные распределения интенсивности для СФП с топологическим зарядом: (а) n = 1, (б) n = 2, (в) n = 3, (г) n = 4. Нижний ряд – полученные интерферограммы для СФП с топологическим зарядом: (д) n = 1, (е) n = 2, (ж) n = 3, (з) n = 4. Размеры картинок – 750 × 750 мкм

На рис. 6 показаны распределения интенсивности и интерферограммы АГВ с n =5 при разных величинах смещения x 0 . Из рис. 6 на интерферограммах видно, что центр сингулярности смещается из области интерферограммы. При этом постепенно пропадает спиральная структура полос интерферограммы.

Заключение

В работе теоретически и экспериментально исследованы асимметричные Гауссовы оптические вихри,

B n ( x , y ) = exp [ in arg ( x — x 0 + iy ) ] =

= [(x - x 0)+ iy ] n / [(x - x 0 )2 + y2 ]

(П1)

На расстоянии z от СФП амплитуду светового по-

ля АГВ можно записать с помощью преобразования

Френеля:

—ik    I   x + y

E n ( ^x , y , ^z ) = -—^ex P I ^ik—;---- I^x

2 n z    к 2z J

Рис. 6. Распределение интенсивности (верхний ряд) и соответствующие интерферограммы (нижний ряд) для Гауссова оптического вихря с топологическим зарядом n = 5 при разных смещениях между центрами СФП и Гауссова пучка: x 0 = 0 (а, д), x 0 = 0,25w (б, е), x 0 = 0,5w (в, ж), x 0 = 0,75w (г, з). Размеры картинок – 750 × 750 мкм

Они получаются при внедрении оптического вихря (изолированного нуля интенсивности с фазовой сингулярностью) в перетяжку Гауссова пучка, так чтобы координаты нуля интенсивности не совпадали с центром перетяжки. Показано, что при распространении такого асимметричного Гауссова пучка нуль интенсивности смещается на бесконечность по прямой, перпендикулярной вектору смещения. Распределение интенсивности вращается таким образом, что на расстоянии Рэлея поворачивается на 45°, а в дальней зоне – на 90° по отношению к положению в начальной плоскости. Получены аналитические выражения для комплексных амплитуд таких пучков, сформированных с помощью спиральной фазовой пластинки и амплитудной голограммы «с вилочкой». Получено аналитическое выражение для орбитального углового момента. Орбитальный угловой момент асимметричного Гауссова оптического вихря дробный и уменьшается квадратично с увеличением расстояния между нулем интенсивности в плоскости перетяжки и центром Гауссова пучка. Уменьшение ОУМ из-за увеличения расстояния между центром Гауссова пучка и координатами изолированного нуля (2), внедренного в Гауссов пучок, объясняется тем, что оптический вихрь внедряется в область с малой световой энергией. Эксперимент качественно согласуется в теорией. Применять такие лазерные пучки с дробным ОУМ можно в качестве накачки нелинейного кристалла для формирования путем спонтанного параметрического рассеяния пары фотонов с перепутанным ОУМ [1, 2]. Отличие АГВ от асимметричных пучков Бесселя [10] и Ла-герра–Гаусса [11] в том, что ОУМ последних растет линейно [10] и квадратично [11] с увеличением степени асимметрии пучка, а ОУМ АГВ убывает с ростом смещения между центрами пучка и голограммы «с вилочкой».

Приложение

Рассмотрим падение Гауссова пучка (1) на СФП с номером n , центр которой смещен от центра Гауссова пучка на величину x 0 и пропускание которой описывается выражением:

^ ^

X j | E 0 (x, y) Bn (x, y )x

—^ —^

x exp I ik

x + y

2 z

( . xx ' + yy ' ) exp I — ik ---------I dxdy .

к z J

(П2)

Переходя к полярным координатам, двойной интеграл в (П2) можно вычислить с помощью справочного интеграла [16]

^

j e~ pr J_n ( cr ) rdr = ( Jnt / 2 V2 p ) x

(П3)

xexP(—t)[I(n—1)/2 (t)— I(n+1)/2 (t)], где t = c2/(8p), а Jn(x) и In(x) – функция Бесселя и модифицированная функция Бесселя n-го порядка.

Тогда вместо (П2) получим:

En ( x ', y ', z ) =

Vn  I iA — B )

I I x

V2 q (z) к V A1 + B1 )

x exp

—

x L) + ikx_±y_

w

2 z

x

(П4)

где

A =

^^^^^^s

kx ' 2 ix

+      , z    w2

Re + i Im t =             ,

2 q ( z ) ²

Re =

( n — 1)/2 ⁽ t )    I ( n + 1)/2

ky '                   iz

B =-- , q ( z ) = 1 +—,

x ' ² + y ' ²

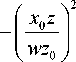
z

z ₀

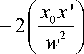
(П5)

I x + y II zn 1 I x. II z I I x x II z

Im = I-----T- II - I— I I I -I + I I

к w J к z J к wJ к z 0 J к w JLz 0

Аргумент t в функции Бесселя в (П4) комплексный, и поэтому трудно сделать определенные выводы об амплитуде АГВ. Из (П4) только видно, что аргумент t зависит от переменной x' и от величины смещения x 0 . Это означает, что вид амплитуды (П4) будет асимметричный, и степень асимметрии будет пропорциональна смещению x 0 . Также видно, что при отсутствии смещения ( x 0 = 0) вид амплитуды совпадает с точностью до постоянной с радиально симметричным Гауссовым оптическим вихрем [17]:

E n ( r , Ф , z ) =

УЛ (—i)n V2q (z)

I. ikr21 exp inф +     x

к      2 z J

(П6)

^x 4?' exp ( ^— t ') ^[ I ( n — 1)/2 ( t ') ^— I ( n + 1)/2 ( t ') ] ,

где t' = (r/w)2 (1 + (iz0/z)) 2| q (z )| 2

.

Так как в эксперименте (рис. 1) измерение распределения интенсивности АГВ происходит в фокальной плоскости линзы, то для сравнения с экспериментом получим вместо (П4) выражение для амплитуды АГВ в дальней зоне дифракции (z >> z0). Из (П5) получим вначале выражение для аргумента t при z >> z0:

t ' = ( krw/2sp2f ) - ( x 0 /4*2w ) , (П7)

где f – фокусное расстояние сферической линзы. Из (П7) видно, что аргумент функций Бесселя и Гауссовой экспоненты в (П4) не зависит от полярного угла ф . Поэтому за асимметрию распределения интенсивности в фокусе сферической линзы отвечает только сомножитель (П4), аналогичный сомножителю F в (5) и равный

F ' =

iA - B

44 + 414

ky  2x0

f   w2

( kx    . 2 x,. 1 ( ky I

1+

УI f   w2 J I f J

(П8)

Из (П8) видно, что сомножитель зависит от переменных x и y несимметрично, и поэтому в интенсивности должна появиться зависимость от полярного угла. Действительно, интенсивность поля (П4) будет пропорциональна модулю квадрата сомножителя F'

IF = |Ff =

4 x 2    k ² r ² 1 4 kx 0 r sin ф

—⁺ ,2 In— w f ) fw

(П9)

( k² r¹ 4 x 2 1

\ ( f2   w4 J

[ 4 kxr 1

+ 1 °- I I ^fw )

cos ф

Из выражения (П9) видно, что минимум числителя (при постоянном r ) достигается при ф = п /2, а максимум - при ф =- п /2. Это означает, что картина дифракции в виде полумесяца повернулась на 90° против часовой стрелки при распространении АГВ от плоскости СФП до фокальной плоскости (так как в перетяжке нуль интенсивности находился на горизонтальной оси в точке x = x 0 ). При этом изолированный нуль интенсивности в фокальной плоскости имеет координаты:

x = 0,

У = x о ( f / z о ).

(П10)

Координаты на оси y нуля интенсивности в (10) и (П10) совпадают, если заменить z на f . Также совпадают выражения (9) и числитель в (П9), если опять заменить z на f и умножить числитель (П9) на ( f / k )². Таким образом, мы показали, что качественно поведение АГВ совпадает при дифракции Гауссова пучка на смещенной СФП (П1) и амплитудной голограмме с «вилочкой» (2).

Работа частично поддержана Министерством образования и науки РФ, грантами Президента РФ поддержки ведущих научных школ (НШ-9498.2016.9) и молодых кандидатов наук (МК-2390.2017.2), а также грантов РФФИ 15-07-01174, 15-47-02492, 16-2911698, 16-47-630483.