DTC-SVM based on interval type-2 fuzzy logic controller of double stator induction machine fed by six-phase inverter

Published Online July 2019 in MECS DOI: 10.5815/ijigsp.2019.07.04

Over the last decade, Alternating Current (AC) motor the most used in industrial applications, these motors divided by the number of stator phases ( q) into several types: two-phase machines (q = 2), three-phase machines (q = 3) and multi-phase machines ( q > 3). Usually, multiphase machines replace three-phase machines in several applications such as; locomotive traction, electric vehicles, rolling mills, mine hoists and cement mills [1,3], because of this machine has high reliability, minimizing the rotor harmonic currents and minimized torque pulsations [2].

The control of the DSIM draws attention to several researchers like scalar control, field oriented control, direct torque control, sliding mode control and back stepping control. The DTC established by I. Takahashi in1980 [4], This latter is used the errors between the estimated and the reference values of flux and torque for minimization the flux and torque errors within the band limits. This scheme is allow us to directly control the inverter states [5]. However, conventional DTC has several drawbacks: difficult to control torque and flux into low speed, large torque ripple, variable switching frequency, torque and current distortion at the change of the sector and high sampling frequency needed for digital implementation of hysteresis bands [5,6].

For the solution of these disadvantages in using multilevel inverter, Space Vector modulation (SVM). In addition, the combination between DTC and SVM produced it a technique called DTC-SVM [11]. This method uses the SVM instead of a switching table to give inverter-switching state and replace the hysteresis band with conventional Proportional Integral (PI) controllers. The PI controllers are simple but cannot robustness control 1 systems with varying parameters or have a nonlinearity [9,10]. Furthermore, fuzzy logic is a scheme used in artificial intelligence and widely utilized in different areas including the control and the automation [15]. The application of interval type-2 fuzzy logic has been a success and it is able to control machines with measurement uncertainties [17]. Does not need a detailed model [18], interval type-2 fuzzy logic controllers are one of useful control schemes to adjust the speed, torque and stator flux of DSIM. In this work, the DTC-SVM-IT2FLC is developed for DSIM in order to evaluate the performance of the system to obtain the integral time-weighted absolute error (ITAE), integral absolute error (IAE) and integral squared error (ISE) for the proposed scheme (DTC-SVM-IT2FLC) and to compare it with other schemes as DTC-SVM-T1FLC and DTC-SVM-PI.

This paper is organized as follows: in section 2, the model of the DSIM and six-phase inverters is presented. Next, we will describe the DTC-SVM by a IT2FLC in section 3. Section 4 shows simulation results for the performance of IT2FLC controller of DTC-SVM-DSIM under various conditions operation. Finally, a general conclusion summaries this work.

• II.    Machine and Inverter Models

• A.    DSIM Model

The DSIM is composed by three winding as follows[3]:

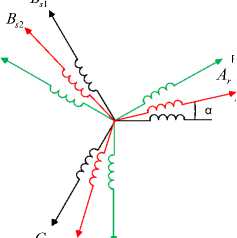
• • Two stator windings, which are shifted by an electric angle of 30°.

• • The rotor winding is shifted sinusoidal repartition by an angle of (120°) relative to the stator windings.

To simplify the model of the DSIM has used set of assumptions have following:

The windings are sinusoidal distributed, the flux path is linear, The two stator windings have the same parameters, core losses and the magnetic saturation are neglected [13].

The windings of the DSIM are shown in Fig. 1;

B r

ROTOR

STATOR 2

^As 2

STATOR 1 A

Cr s1

C s 2

Fig.1. DSIM winding representation.

The model of DSIM is set a nonlinear differential equations, using the vector space decomposition, its T matrices of transformation [7]:

	1	1 — 2	1 — 2	3 2	3 — 2	3 — 2
	0	3	3	1	1	1
		2	2	2	2	2
T s ( a ) ] =	1	1 —	1 —	3 —	3	0
		2	2	2	2
				1	1
	0	0	0			-1
				2	2
	1	1	1	0	0	0
	.0	0	0	1	1	1

The voltage, Current and flux space vectors of the DSIM can be mapped into two-dimensional orthogonal subspaces: α1-β1, α2-β2 [7].

• Electrical equations

Г к 1 v sa 1		■ Rs 1	0	0	0	0	0 "	I s a 1
V.		0	R s 1	0	0	0	0	I s p 1
V s a 2		0	0	R s 2	0	0	0	1 s a 2
у r se 2		0	0	0	Rs 2	0	0	I s P 2
0		0	0	0	0	R r	0	I ™	(1)
. 0 J		. 0	0	0	0	0	R r J	. I r e _
+
L s 1	0	0	0	0	0 "		"Ф s a 1 "
0	Ls 1	0	0	0	0		Ф в
0	0	Ls 2	0	0	0	d	Ф s a 2
0	0	0	Ls 2	0	0	dt	Ф s e 2
0	0	0	0	L r	0		ф r a
. 0	0	0	0	0	L r J		Ф r e _

• Flux equation;

Ф sa 1		" L s 1 + L m	0	L m	0	L m	0   ’	" Isa 1
Ф в		0	L s 1 + L m	0	L m	0	Lm	I se 1	(2)
Ф sa 2		L m	0	L s 2 + L m	0	L m	0	I sa 2
Ф sP 2	^	0	L m	0	L s 2 + L m	0	Lm	I s» 2
Ф ra		L m	0	L m	0	L r + L m	0	I ra
. Ф re		.    0	L m	0	L m	0	L r + L m J	[ I e

• Equation of electromagnetic torque;

• Mechanical Equation;

dt

• B.    Six-Phase Inverter Model

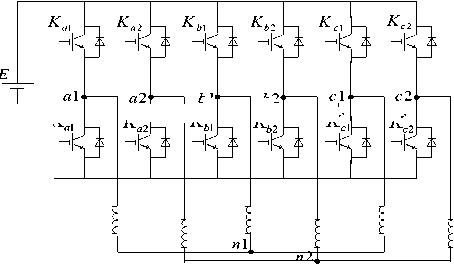
The stator windings of DSIM are fed by a six-phase inverter as illustrate in Fig. 2[6,7].

K ^'

K

K ^'

K

o

Fig.2. Schematic diagram of a six-phase inverter.

b 1

K ^'

b 2

K ^'

K a1 ,K b1 ,K c1 : The switches of the upper half bridge.

K a2 ,K b2 ,K c2 : The half bridge inferior.

o: The neutral point of the source.

n ₁ ,n ₂ : The neutrons of stator 1 and stator 2.

sequence components since the neutral are not relies. Therefore:

V a1 + V + V c1 = 0

V sa 2 + V sb 2 + V sc 2 = 0

t в 1

20 62

14     13

L1

57    48

L3

54 ^L4 32

1 43

The voltage vector of the six-phase inverter is

expressed as follows[6]:

L2

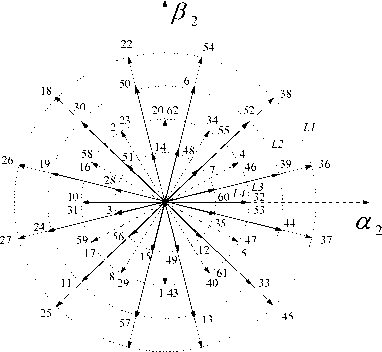
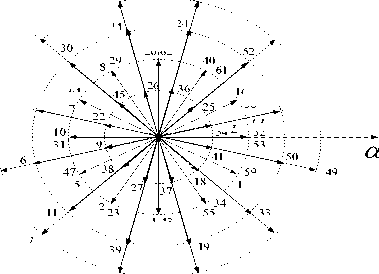
Fig.3. Inverter voltage vectors in α1 - β1; α2 - β2 subspace.

Fig.3 illustrate a total of The 64 voltage vectors can be projected into the subspaces of (α 1 ,β 1 ) and (α 2 ,β 2 ) from combining all the states of the switches 12[6], where we note that each case is represented by a decimal number based on binary value of S a1 ; S b1 ; S c1 ; S a2 ; S b2 ; S c2 [7].

S a;b;c (1 ; 2 ; 3) = (0 ; 1).

L1, L2, L3 and L4 : The amplitudes of four groups for the voltage vectors.

The phase voltage can be expressed as follows[6]:

Vsa 1	Va 1 n 1	Va 1 o	+ Von1
V	Vb 1 n 1	Vb 1 o	+ Von1
V	Vc 1 n 1	Vc 1 o	+ Von1	(5)

Vsa 2	= y, , a 2 n 2	= V a 2 o	+ V on 2
V sb 2	= V r b 2 n 2	= V b 2 o	+ Von 2
у I V sc 2	= v. ? c 2 n 2	= V c 2 o	+ Von 2

Assuming that the windings of the stator 1 and stator 2 are balanced, the phase voltage cannot contain zero

V sa 1 "		" 2	—1	—1	0	0	0 "	"Va 1 o "
Vsb 1		— 1	2	—1	0	0	0	Vb 1 o
Vsc 1		— 1	—1	2	0	0	0	V c 1 o	(6)
Vsa 2	■	°	0	0	2	—1	— 1	V a 2 o
Vsb 2		0	0	0	—1	2	— 1	V b 2 o
V sc 2 _		_ °	0	0	—1	—1	2 _	V c 2 o _

[ V s ] = C K d ] [\ ] = E [ S ] = E [ S a 1 S a 2 S b1 S b 2 S_C 1 S_C 2 ]

III. DTC-SVM-DSIM Strategy Control

Fig. 4 show the proposed DTC-SVM with IT2FLC scheme of DSIM fed by six-phase inverter. This method suggest the use of three controllers of interval type-2 fuzzy logic for speed, torque and stator flux to replace the classical PI. The exit of controllers of the torque and flux generate the references stators voltages components ( U X 1 ;U Y 1 ) ( U X 2 ; U Y 2 ). This components are continuous voltage commands and then transformed into stationary coordinates ( α - β ) the controlled values ( U_{α 1} ; U β ₁ ) and

( U_{α 2} =0 ;U β ₂ =0) are delivered to SVM which give rise to switching signals S_{a 1} ; S_{b 1} ; S_{c 1} ; S_{a 2} ; S_{b 2} ; S_{c 2} for the six phase inverter [6,7,8].

A. Flux and Torque estimations

In this part, estimating the amplitude and angle position of stator flux and torque. So[11]:

Фsk(a,P) = J (Vsk(a,в) — RsIsk(a^) )

ˆ         ˆ 2      ˆ 2(8)

sk    \ ska       ske

^sk = arctg

Ф ,

C em = P

' ((Ф s оЛ 1 в

\    sk a у

^{— Ф} s 1 e I s 1 a ^{) + ( ф} s2 a ¹ s 2 в

—

ˆ

^Ф s 2 в I s 2 a

)  (1°)

and k=(1;2)

B. Space vector with Modulation

In this part, estimating the amplitude and angle position The objective of the SVM technique is to give the switching signals of the six phase inverter. The preciseness of the control scheme depends on the precision estimation of the amplitude of the torque and

the amplitude and position of the stator flux. A proposed SVM scheme of the DSIM is based on two steps, The first is to use two original switching vectors to synthesize the new vectors by forcing the second volts means of the voltage vectors in the subspace α2-β2 to zero (Uα2 = 0, Uβ2 = 0). The second is to use two synthesized vectors without harmonics to compose the Vref reference voltage vector based on SVM classical [6,8].

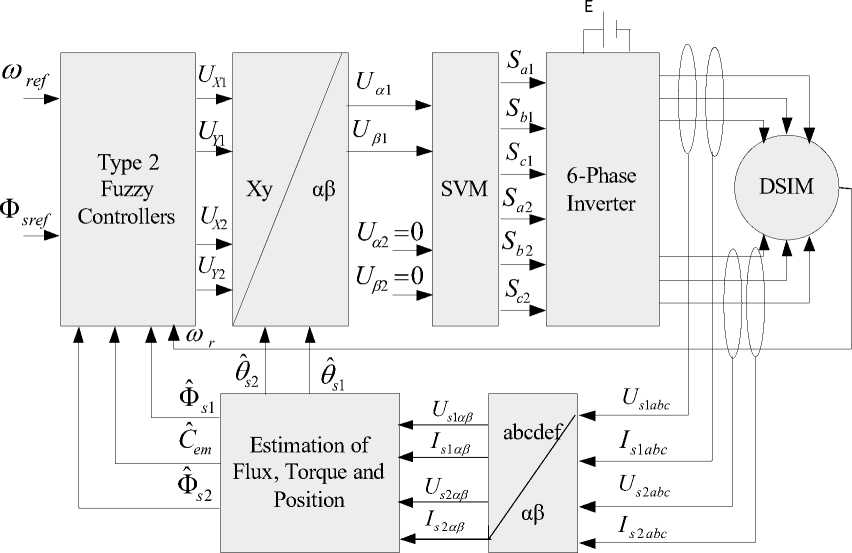
Fig.4. Proposed of DTC-SVM with Interval type-2 fuzzy logic control strategy

For example, the new vector V ₃ is synthesized by vector 24 and vector 60, and has the amplitude of 0.598 E in α 1 -β 1 subspace and zero in α 2 -β 2 subspace (Fig. 5).

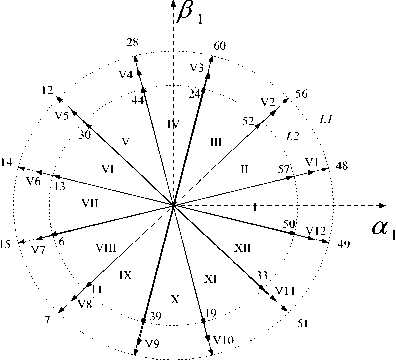
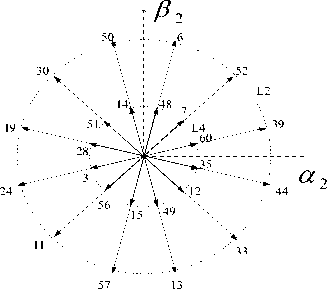
Fig.5. Selected and synthesized vectors in α1 - β1; α2 - β2 subspace.

In each sector, every voltage vector is composed from basic space voltage vector of the four side of sector (V a , V b , V c , and V d ) and one zero vector:

Va, V b , V c , and V d : The original voltage vectors.

V ac ,V bd : are newly composed vectors in the first step.

For example, The vectors 28, 44, 24 and 60 are used to compose the reference voltage vector V ref from a two-step synthesis process in sector IV. As shown in Fig. 6.

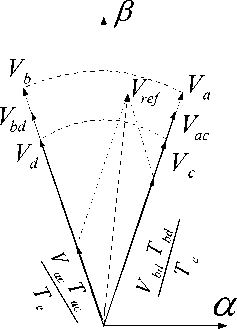
Fig.6. Projection of the reference voltage vector in sector IV.

The calculated times T ₁ , T ₂ , T ₃ and T ₄ are applied to the switches to produce space vector of six phase inverter switching patterns based on every sector.

For this, using four equations with four unknown times as follows (V sα1ref ; V sβ1ref ),(V sα1ref = 0; V sβ1ref = 0) [8]:

fTV +TV +TV +TV -TV

• ¹1 ^vs « 1 ^{+ A}2 ^vs a 2 ^{+ A}3 ^vs a 3 ^{+ 1}4 ^v s a 4 ^Ae ^vs a 1ref

TV + TV +TV +TV = T V

• ^T 1 ^V s в 1 ^{+ T} 2 ^V s в 2 ^{+ T} 3 ^V s в 3 ^{+ T} 4 ^V s в 4 T e V s ^ 1ref

• (11)

• ¹1 ^V s a 1 ⁺ V V s a 2 ⁺ V V s a 3 ⁺ V V s a 4 V V s a 2ref ^u

TV +TV +TV +TV -TV  -0

T I V s e i ^{+ T} 2 ^V s в 2 ^{+ T} 3 ^V s в 3 ^{+ T} 4 ^V s e 4 T e V s в 2ref 0

V sα1 V sβ1 : Reference value of tension ; Times T i denote the required on-time of the active-state vectors V i during each sample period T e ; T n denote time of the null state vectors

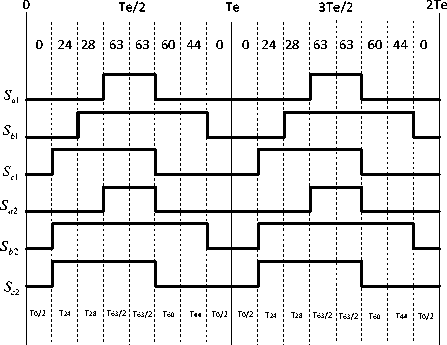
Fig.7. Leg voltages and space vector disposition in sector IV.

Fig. 7 shown The leg voltage in one switching period for sector VΙ. the signals should be distributed symmetrically to the middle of the PWM period to reduce the switching number [6].

• C. Design of Interval Type 2 Fuzzy Logic Controller

In this section, the interval type-2 fuzzy logic controller replaced the PI controller for to reduce the time response while preserving the system stability and cancel the static error. Generally, the IT2FLC can handle complicated non-linear systems which have a degree of uncertainty [17]. It does not need a precise model of the system and the exact values of the parameters[18].

The interval type-2 fuzzy logic contain four elements are[17,19]:

• •    Fuzzification:   convert classical data into

Membership Functions (MFs) such as NB (Negative Big), B (Big).....

• •    Fuzzy Inference Engine: this element depends on the lookup table, which summarizes our control derivatives resulting, from the link that combines the control rules and MFs.

• •    Type Reducer: this component of interval type-2 fuzzy logic, to reduce the type-1 fuzzy set output and transfer to the defuzzification.

• •    Defuzzification: type reducer you take a type-1 fuzzy set output, and the defuzzification to convert MFs into crisp data.

The DTC-SVM use the IT2FLC give an excellent system performance. In this part, we use three IT2FL controllers for the speed, the torque and the stator flux. The structure of a interval type-2 fuzzy logic system is illustrated in Figure 8 [17]

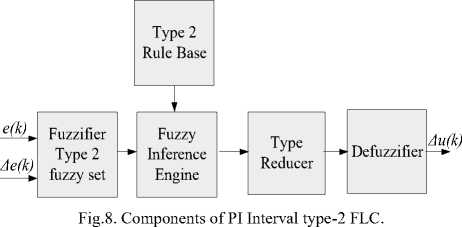
The inputs of the IT2FLC are the error and its variation:

e (k ) = Xref (k)-Xr (k)

A e ( k ) = e ( k ) - e ( k - 1 )

And X=( speed rotor, electromagnetic torque and stator flux ).

The PI-IT2FLC as shown in Fig. 9;

Fig. 10, presents the membership function of the IT2FLC that is used for both the torque and flux controlling and speed regulation to improve the dynamic performance (see Fig. 11). The membership functions are assigned with three fuzzy sets which are P, Z, N for the torque and stator flux and seven fuzzy sets which are PB, PM, PS, Z, NS, NM, NB for the speed.

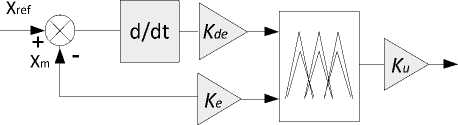
Fig.9. Bloc diagram of PI-IT2FLC.

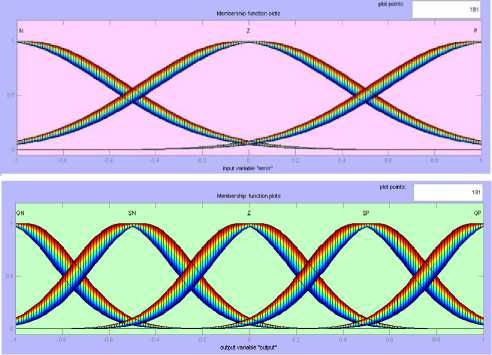
Fig.10. Membership function of error torque and error flux and variation.

Fig.11. Membership function of error speed and variation

Table 1. Rule Base of Speed IT2FLC

U		e
		NB	NM	NS	EZ	PS	PM	PB
de	NB	NB	NB	NB	NB	NM	NS	EZ
	NM	NB	NB	NB	NM	NS	EZ	PS
	NS	NB	NB	NM	NS	EZ	PS	PM
	EZ	NB	NM	NS	EZ	PS	PM	PB
	PS	NM	NS	EZ	PS	PM	PB	PB
	PM	NS	EZ	PS	PM	PB	PB	PB
	PB	EZ	PS	PM	PB	PB	PB	PB

Table 2. Rule Base of Torque and Flux IT2FLC

U		e
		N	Z	P
de	N	NB	NS	PS
	Z	NB	Z	PB
	P	NS	PS	PB

• V.    Result and Duscussion

The proposed scheme of the DTC-SVM using three IT2FLCs of DSIM fed by a six-phase inverter (see Fig 12) and the estimation block of torque and stator flux (see Fig. 13) is realized with SIMULINK/MATLAB, while the DSIM’s parameters are define by:

The simulation work consists of two tests for robustness studies:

• A. Speed and Torque variation

In the first test; the DSIM runs with speed variation values of 100rad / s during] 0-2] s; 157 rad / s for the duration of] 2-4] s; 78.5 rad / s for the duration of] 4 -6] s; -78.5 rad / s for the duration of] 6-8] s. And the torque variation with the sign of the load torque (14 Nm, -14 Nm) for at the periods of (3 s, 7 s).

Table 2. represents the linguistic rule base, which introduces a IT2FLC [18].

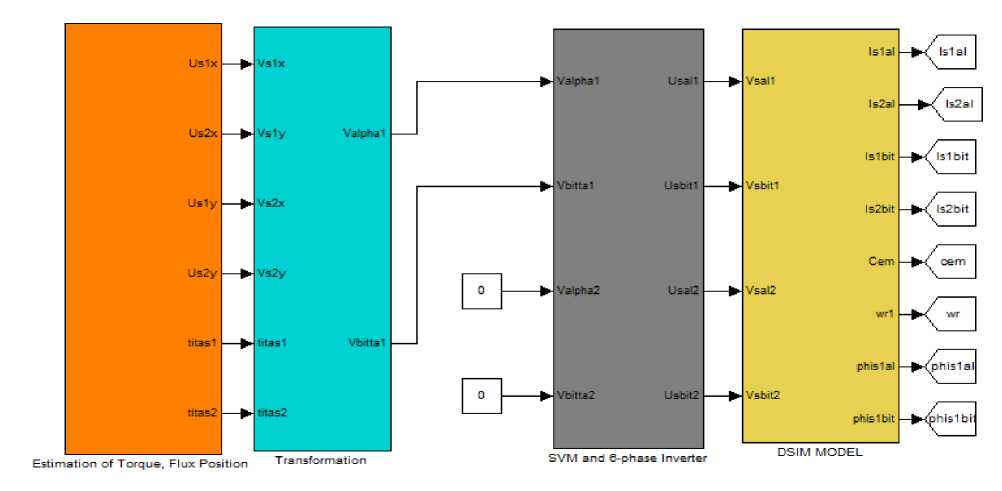
Fig.12. Simulink bloc of DTC-SVM based on IT2FLC of DSIM

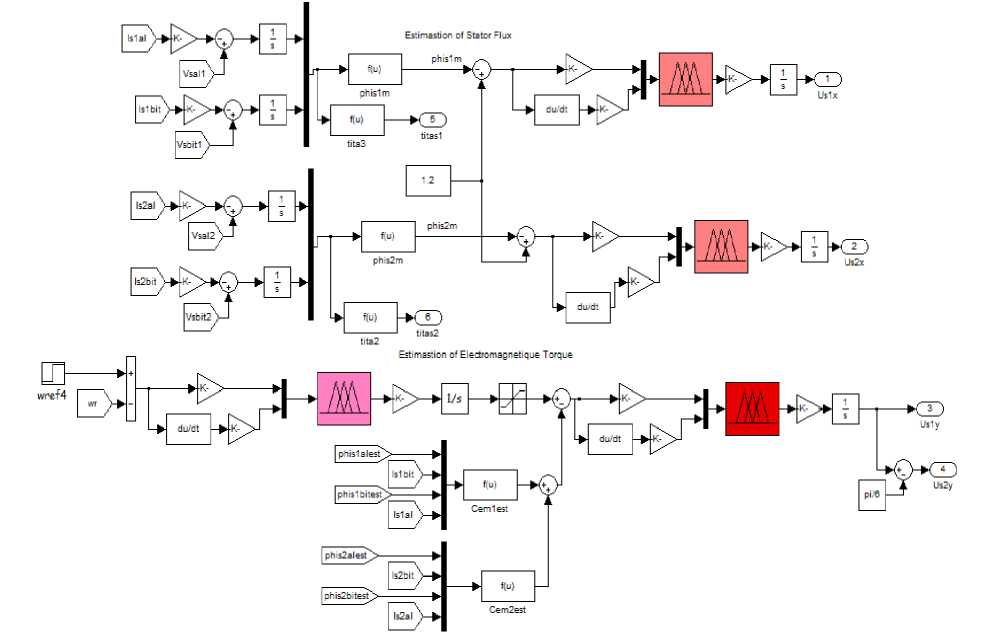
Fig.13. Simulink bloc of the torque and the stator flux estimator

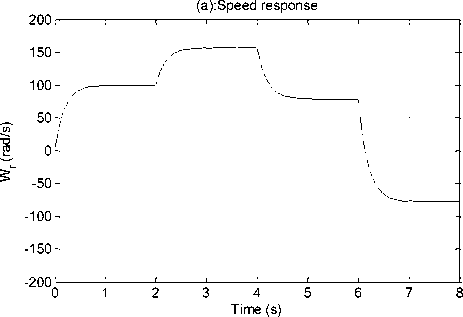
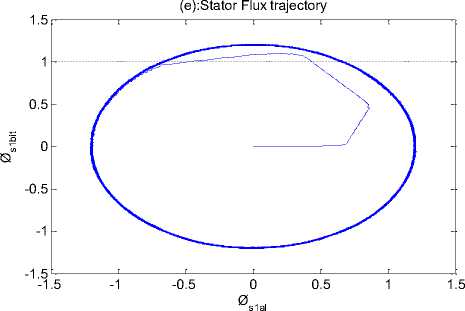
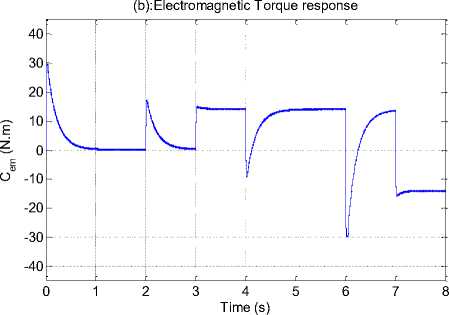
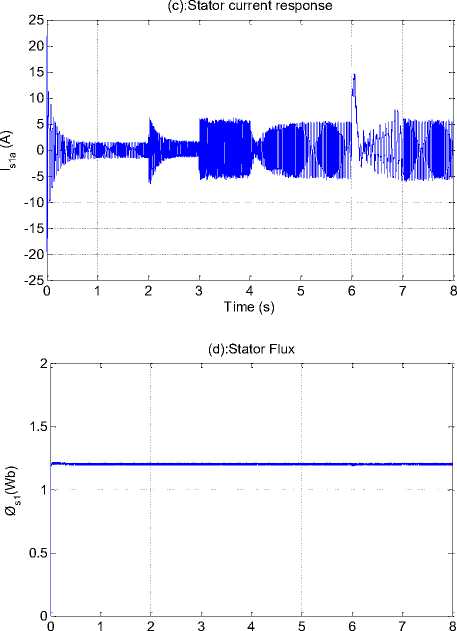
Fig.14. DSIM simulation result with variation of speed and load torque.

Time (s)

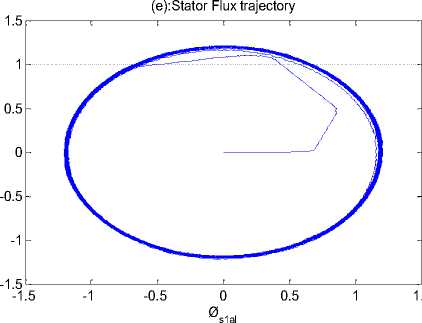
Fig. 14 shows that responses of the change in command speed and load torque for DTC-SVM of DSIM using the proposed IT2FLCs, We note that when the motor starts, the speed reaches its very quickly the desired reference speed (Fig.14 (a)), the mechanical torque increases to reach the peak value (30 N.m) and falls down to be close zero value because the motor running with no load. At we changed the value of load torque to reference, the motor output torque increase to cover this load (Fig. 14 (b)). The response of stator current and amplitude stator flux a produced by motor illustrates in (Fig. 14 (c), (d)). Almost circular flux trajectory with equal amplitudes in both α and β axes (Fig. 14 (e)). This test has for object the study of controller behavior in pursuit and in regulation.

B. Robust control for the internal and external disturbances

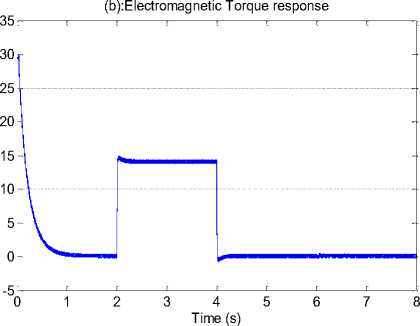
The second test in order to confirmed the robustness for control strategy against the external disturbances (represented by the nominal load torque), these variations impose an applied to 14 N.m between (2-4) sec and the internal disturbances (represented by parametric variations), the parametric variations represented by increase of 100% as of the stator resistances 1,2; R s11 = 2* R s1 = 2*R s2 and moment of inertia J 1 = 2 *J at t= 6 s.

(a):Speed response

Time (s)

^{Ø s1bit}                                                    Ø_s1(Wb)                                                   ^I s1a ^(A)                                                  C (N.m)

(c):Stator current response

Fig. 15 shows the behavior of propose scheme when the external disturbances and the parameter variations, Influence of the external disturbances and the parameter variations on the speed, electromagnetic torque, stator current, stator flux response is shown in Fig. 10 (a), (b), (c), (d). This test confirms the effectiveness and flexibility of the proposed control method.

In order to carry out DTC-SVM control of the DSIM using fuzzy logic controllers, the quantitative comparison between T1FLC and T2FLC [16].

The values that are obtained for ISE , IAE and ITAE at the simulation time (8 sec) for the two tests are summarized in Table 3.

Time (s)

Table 3. Performance criteria values for pi, type-1and INTERVAL type-2 fuzzy logic controllers.

Tests	Index	DTC-SVM-PI	DTC-SVM-T1FLC	DTC-SVM-IT2FLC
Test 1	ISE	2.947	2.78	2.052
	ITAE	10.62	7.149	6.514
	IAE	1.764	1.666	1.53
Test 2	ISE	1.828	0.705	0.5118
	ITAE	4.119	0.9787	0.8437
	IAE	1.778	0.6385	0.5461

From the results obtained in Table 3 it is noted that the values of ISE , IAE and ITAE for the interval type 2 fuzzy logic controller is inferior relative the type 1 fuzzy logic and PI controllers.

DSIM simulations results with the external disturbances and the internal disturbances.

• VI.    Conclusions

In this paper, a new DTC-SVM for a double stator induction machine supplied by a six-phase inverter based on a type-2 fuzzy logic controllers was presented. We have established and simulated a mathematical model of the DSIM and the six-phase inverter and the DTC-SVM using MATLAB-SIMULINK to study the static behavior and dynamics of the DTC-SVM system.

In order to overcome the drawbacks of DTC, we will combine the SVM technique and IT2FLC. It has several advantages:  constant switching frequency, excellent response, minimal ripples, low harmonics and good waveform of the stator phase current. The IT2FL controllers offer excellent performance and robustness were verified by simulation.