Два способа организации скалярного произведения в методе граничных состояний

Funding information: The study was carried out with the financial support of RFBR and the Lipetsk Region as part of the research project No. 19-41-480003 "p_a".

Введение. Краевые задачи теории упругости в механике достаточно изучены, поэтому в последние годы проводятся исследования частного направления. Например, рассмотрена осесимметричная первая основная задача для полуполосы [1], решение которой строится в виде разложений по системам функций Фадля-Папковича и имеет явный вид. Предлагается общий метод решения первой основной задачи теории упругости для прямолинейно-анизотропного тела в случае плоской деформации [2]. Используются замкнутые системы краевых задач, схожих с задачами Гильберта, что позволяет добиться большей общности метода. Методом конечных элементов на основе вариационного принципа Кастильяно решены плоские изотропные задачи [3]. Это позволило получить поля напряжений на сетках достаточно низкой размерности, в том числе для несжимаемых материалов. Решаются контактные задачи о внедрении эллиптических штампов в трансверсально-изотропное упругое полупространство [4].

Метод граничных состояний при решении краевых задач для анизотропных тел также нашел свое применение. Например, рассмотрено упругое равновесие трансверсально-изотропного цилиндра под действием осесимметричных поверхностных сил [5]. Исследуются задачи кручения протяженных цилиндров из материала с анизотропией общего вида [6]. Показана математическая модель получения явных параметрических решений для изотропных и анизотропных тел [7, 8], где константы среды в качестве параметров включены в упругие поля. Разработана методика решения задач теории упругости средствами компьютерной алгебры [9]. В решении задач напряженно-деформированной неограниченной упругой среды, содержащей сферические полости или включения, при разных условиях применен метод граничных состояний [10].

В настоящей работе исследуются два подхода к назначению скалярного произведения в «теле» метода граничных состояний. При этом проводится тестирование каждого состояния на примере решения первой основной задачи теории упругости. В каждой задаче удерживается одинаковое число используемых элементов и оценивается уровень погрешности.

Материалы и методы. Метод граничных состояний (МГС) [11] является энергетическим, в нем применяется фундаментальная теория рядов для решения основных задач механики. В качестве опорных используются понятия внутренних и граничных состояний. Внутреннее состояние ξ обусловлено набором вектора перемещений u , тензора деформаций ε и тензора напряжений Т:

ξ= { u , ε , Т }.                                                        (1)

Граничное состояние обусловлено набором вектора перемещений точек границы u v и усилий p на границе тела:

γ= { u^v , p }.

Совокупность таких состояний образует базисы пространств внутренних ξ= { ξ ₁, ξ ₂, ξ ₃, ..., ξ _k ,... } и граничных Г = { γ ₁, γ ₂, γ ₃,..., γ _k ,... } состояний. Далее проводится ортогонализация базисов состояний, где в качестве орто-гонализатора в базисе граничных состояний используется выражение:

( ξ i , ξ j ) =∫ ε i T j dV ,

V в базисе граничных состояний ― выражение:

( γ _i , γ _j ) =∫ u_i^vp_jdS .                                                             (2)

S

Каждому элементу ξ k ∈ Ξ соответствует единственный элемент γ k ∈ Г , причем это соответствие взаимнооднозначное: ξ k ↔γ k . Это позволяет отыскание внутреннего состояния свести к построению изоморфного ему граничного состояния. В случае первой основной задачи искомые внутреннее и граничное состояния представляет собой ряд Фурье:

∞∞

ξ=∑ckξk; γ=∑ckγk,(3)

k=1

здесь c k ― коэффициенты Фурье:

ck= ∫ pukdS ,(4)

S где p ― вектор заданных поверхностных сил; uk ― вектор перемещения в k-ом базисном элементе базиса внутренних состояний. При этом базисные наборы формируются на основании общего или фундаментального решения задачи.

Первые общие решения уравнения Ламе линейной теории упругости были построены еще в 30-е годы прошлого столетия. Уравнение Ламе ― это уравнение движения (в рассматриваемом случае ― равновесия) Эйлера:

∇T+f=0, где Т ― тензор напряжений; ∇ ― оператор Гамильтона, действующий как дивергенция; f ― массовые силы.

В уравнении Ламе тензор напряжений Т в соответствии с законом Гука представлен через тензор деформаций ε . В свою очередь тензор деформаций в соответствии с соотношением Коши представлен через вектор перемещений u. В общих решениях уравнения Ламе вектор перемещения определяется: в теории изотропной упругости через гармонический вектор В и гармонический скаляр, в теории анизотропной упругости ― через функцию напряжений F.

Вектор В (функция F) может быть представлен в виде ряда по базисным векторам B k = B k ( α i ) ― функциям координат α i . В результате каждому гармоническому базисному вектору B k (функции F k ) будут поставлены в соответствие следующие базисные элементы:

• •   вектор перемещения u k ;

• •   тензор деформаций ε k ;

• •   тензор напряжений T k ;

• •   вектор массовых сил f k (из уравнений равновесия);

• •    вектор поверхностных сил (из фундаментального соотношения Коши):

p_k = nT_k , где n ― внешняя единичная нормаль к поверхности тела.

Механика

По перечисленным базисным элементам соответствующие векторы или тензоры разлагаются в ряды Фурье с одинаковыми коэффициентами c k , которые определяются из условий ортогональности базисных функций. Например, для первой основной задачи при отсутствии массовых сил, когда на всей поверхности тела S заданы внешние силы р и осуществлена ортогонализация базисных векторов p k ( ∫ p i p j dS =δ ij ― дельта Кро- S

некера), коэффициенты c k определяются из выражения:

c k = 1 PPkdS -                                          (5)

S

Это выражение вытекает из представления:

Р = Z c_kP_k .

k = 1

Таким образом, исследуется способ формирования решения с помощью выражения для скалярных произведений в базисе граничных состояний:

⁽ Y / > Y j ) = 1 Р iP j dS                                                ⁽⁶⁾

S и выражения для коэффициентов Фурье (5).

В случае второй основной задачи имеют место зависимости:

⁽ Y z , Y j ) = 1 u v u j dS ;

S ck = 1 uuvdS,

S где u — заданный вектор перемещения точек границы тела; u j — вектор перемещения в к- ом базисном элементе базиса граничных состояний.

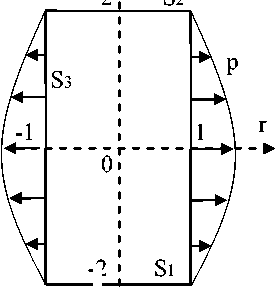
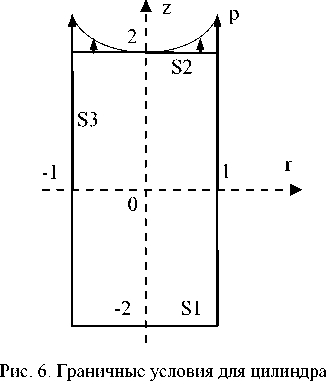
Результаты исследования. Параметры скорости сходимости рядов и точности результата рассмотрим на примере решения задачи об упругом равновесии трансверсально-изотропного цилиндра из темно-серого алевролита [12] в безразмерном виде (рис. 1).

Граничные условия:

Р = 0, S j z = - 2,0 <  r <  1;

р = 0, S ₂1 z = 2, 0 <  r <  1;

p_r = 4 - z ², P z = 0, S з| r = 1, - 2 <  z <  2.

<_>

4 z

-2

Рис. 1. Граничные условия для транстропного цилиндра

Подробно методика решения первой основной задачи традиционным способом с помощью скалярного произведения (2) приведена в работе [6]. Базис внутренних состояний (1) строится следующим образом:

• •    используя общее решение задачи о плоской деформации [13], конструируются базисные наборы плоских вспомогательных состояний;

• •    по формулам перехода определяются базисные наборы пространственных осесимметричных состояний;

• •    проводится ортонормирование базиса внутренних состояний по матричному алгоритму Грама-Шмидта с использованием скалярного произведения (2);

• •    из ортонормированного базиса внутренних состояний редуцируется ортонормированный базис граничных состояний;

• •    вычисляются коэффициенты Фурье (4) и строятся ряды (3) в развернутом виде (индекс к помещен наверх):

∞k         ∞k          ∞k         ∞k u = Z ckui ; р, = Z ckPi ; Qy = Z ckQj; sj = Z cksj.

к = 1                    k = 1                      k = 1                     k = 1

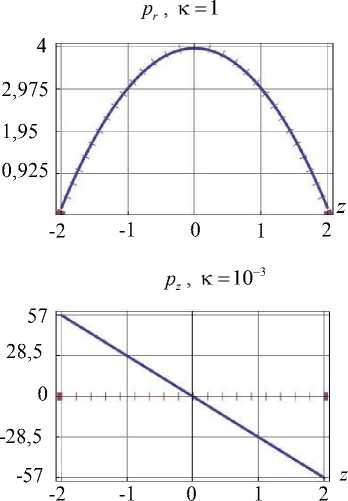
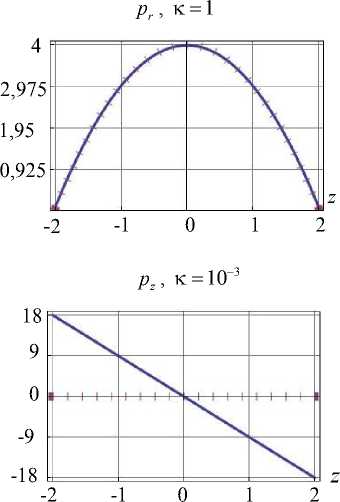
Опустим информацию о полях характеристик напряженно-деформированного состояния, полученных при одном и другом способе назначения скалярного произведения, и приведем лишь основные результаты. При этом назовем традиционный подход, используемый в [11], как первый способ решения задачи, а подход, использующий скалярное произведение (6) и коэффициенты Фурье (5), как второй способ. Точность решения при удержании одинакового числа базисных элементов у второго способа выше. На рис. 2 для каждого способа приведено сопоставление полученных граничных условий (ГУ) с заданными при использовании 8-ми значений коэффициента Фурье. Усилия изображены в масштабе, например, истинное значение p r на первом графике рис. 2 равно значению на графике, умноженному на коэффициент к .

<…>

1-й способ                                2-й способ

S 1

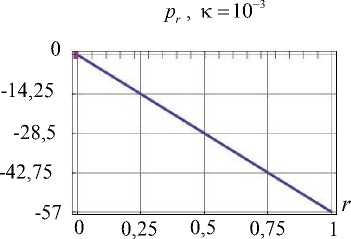
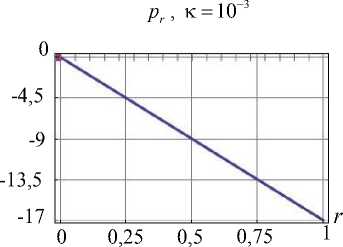
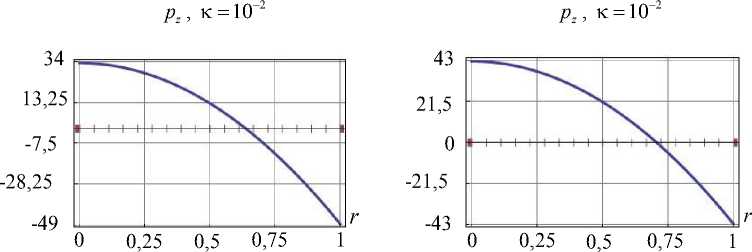
Рис. 2. Верификация ГУ для цилиндра при 8-ми элементах базиса

Механика

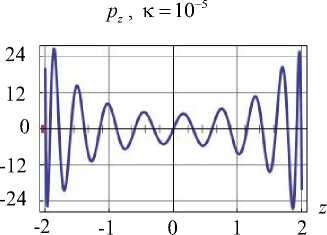
Эта тенденция сохраняется и при увеличении числа используемых элементов базиса. Для 61-го элемента верификация граничных условий представлена на рис. 3 (приведено сравнение силы pz на участке границы S3 ). Если оценивать погрешность как максимальное отклонение полученной величины от заданной, то во вто- ром способе погрешность меньше.

<...>

1-й способ

2-й способ

^S 3

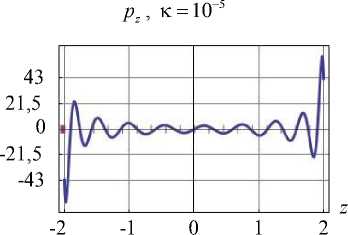
Рис. 3. Верификация ГУ для цилиндра при 61-м элементе базиса

Далее исследуем точность решения для трансверсально-изотропного тела вращения неканонической формы (рис. 4). Граничные условия:

P = 0, 5 1 и 5 2 ;

p_r = 0, p_z = 0,25, 5 з | z = 1,0 <  r <  1;

p_r = 0, P z =- 1, 5 4, z = - 1,0 <  r <  0,5.

Удержано 15 элементов базиса. На рис 5. представлено сравнение граничных условий для каждого способа (показаны не все участки границы и компоненты вектора сил).

<…>

1-й способ

2-й способ

^S 4

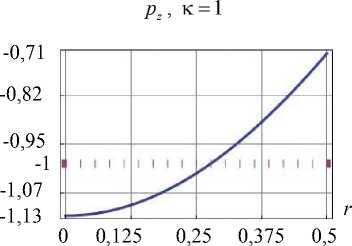
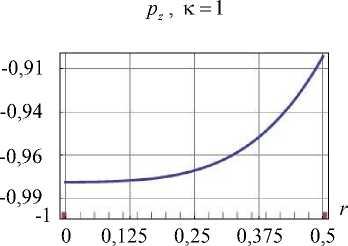
S 3

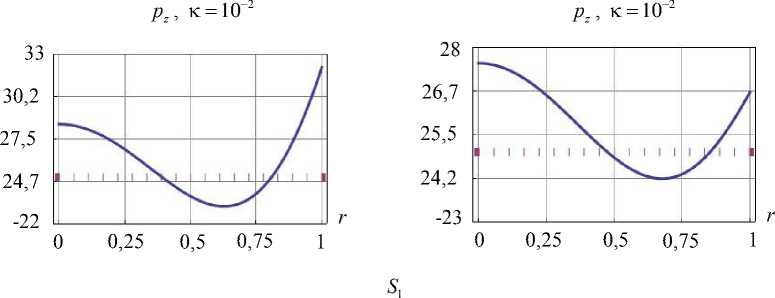
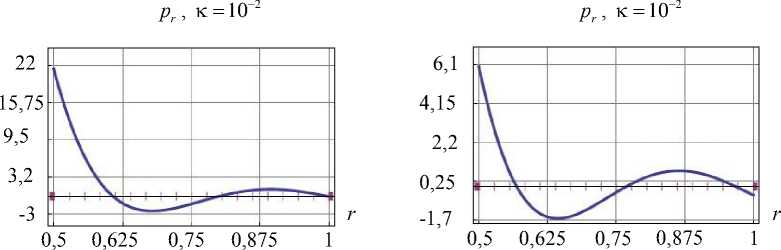
Рис. 5. Верификация ГУ для тела вращения

Как видно из графиков, для тела более сложной формы отличие в скорости сходимости наблюдается в пользу второго способа. Рассмотрим задачи с участием массовых сил. Последовательность формирования решения следующая:

1. Задается зависимость вектора перемещения плоского вспомогательного состояния от координат y ^α z ^β и на его основе определяется вектор перемещения пространственного осесимметричного состояния.

2. Для такого вектора определяются параметры:

• тензор деформаций по соотношению Коши;

• тензор напряжений из закона Гука;

• усилия на поверхности тела из фундаментального соотношения Коши;

• массовые силы из уравнения равновесия.

3. Строится точное частное решение задачи, соответствующее заданной в каждой точке тела функции перемещения.

Механика

• 4.    Перебирая а + в <  n ( n = 1, 2, 3 ...), строится множество точных частных решений задачи линейной теории упругости для параметров:

• •   векторы перемещения u k ;

• •    тензоры деформаций E k ;

• •    тензоры напряжений Т k ;

• •   векторы поверхностных сил p k = n • Т_k ;

• •    векторы массовых сил X_k .

• 5.    Формируются   базисы пространств внутренних В^^, ^ ₂, ^ ₃,..., ^ _k ,... }    и граничных

• 6.    Оставляем среди этих решений только линейно независимые и осуществляем их ортогонализацию в соответствии со скалярными произведениями в базисах внутренних и граничных состояний:

Г = { Y i , Y ₂, Y ₃,—, Y _k ,— } состояний, в которых соблюдаются равенства:

^ k = { u k , E k , Т_к },

Y k = ^{ u k , P k , X k ^} .

G i , ^ j ) = J_E j ) а j ) dV ,

V

( Y i , Y j ) = J P ii ) u Vi ) dS + J X k i ) u ij ) dV

SV

(индексы i и j , отвечающие за номера элементов, помещены наверх и заключены в скобки).

• 7.    В результате получаем базис, по которому соответствующие векторы или тензоры разлагаются в ряды (3) с одинаковыми коэффициентами:

c_k = k Xu_kdV + J pu^v v dS ,

VS где X — вектор заданных массовых сил.

Исследуем возможность построения упругого поля при наличии массовых сил, используя соотношения (6) и (5). Рассмотрим первую основную задачу с неуравновешенными усилиями для трансверсально-изотропного цилиндра (рис. 6). Граничные условия:

p = 0, S j и S з ;

p_r = 0, p_z = r ², S з | z = 2, 0 <  r <  1.

Выражения для ортонормированного базисного набора компонент вектора перемещения u = { u , w } приведены в табл. 1.

Таблица 1

Ортонормированный базисный набор компонент вектора перемещения

	u	w
5 1	0	0,1213 z
-	0,0788 r	- 0,1126 z
-	0	0,0331 z 2
~ .	0,0592 rz	- 0,0268 z 2
-	- 0,02 rz	0,0975 r 2 + 0,009 z 2
- •	0,1535 r	- 0,9163 z + 0,0691 z 3
-	- 0,2896 r + 0,0724 rz 2	1,2067 z - 0,1005 z 3
-	1,8629 r - 0,4824 rz 2	- 8,2447 z + 0,4824 r 2 z + 0,6701 z 3
-■	0,0908 rz	- 0,0454 r 2 - 0,4347 z 2 - 0,0511 z4
5 10	- 0,1757 rz + 0,0439 rz 3	- 0,0195 r 2 + 0,3661 z 2 - 0,0457 z4
5 11	0,2881 rz - 0,0804 rz 3	- 0,144 r 2 - 0,7209 z 2 + 0,1206 r 2 z 2 + 0,0837 z4

Для получения строгого решения потребовалось 11 коэффициентов Фурье, ненулевые значения: с = 0,2178; с ₂ =- 0,1226; с 3 = 0,2377; с 4 =- 0,0732; с ₅ = 0,0247; с ₈ = 0,1443; с 11 = 0,1443. Приведем выражения для перемещений и массовых сил (удержано 4 знака после запятой):

u = 0,2592 r + 0,0367 rz - 0,0696 rz ² - 0,0116 rz ³;

w = - 0,0183 r ² - 1,1497 z + 0,0696 r ² z - 0,094 z ² + ;

+ 0,0174 r ² z ² + 0,0967 z ³ + 0,0121 z ⁴;

R = - 0,2814 r - 0,1407 rz ; Z = 1,2012 - 0,25 r ² - 3,6038 z - 0,9 z ².

Если построить базис внутренних состояний через плоские вспомогательные состояния, образованные с помощью монома z ^a y ^e , то ортонормированный базис и коэффициенты Фурье изменятся. В этом случае решение окажется тоже строгим и примет вид:

u = 0,0363 r - 0,0913 rz + 0,0309 r ³ z - 0,0287 rz ²;

w = 0,0456 r ² - 0,0077 r ⁴ - 0,4148 z + 0,0287 r ² z + 0,0257 z ² + 0,0399 z ³;

R = - 2,0145 r - 1,6178 rz ; Z = - 0,25 r ² - 1,4893 z .

Аналогично можно получить другие частные решения задачи, используя при формировании базиса полиномы разного вида, например, z ^а y ^e+ z ^а и др.

Исследуемый подход позволяет получить множество решений одной краевой задачи теории упругости при наличии массовых сил. Подвержены перемещения и массовые силы, сочетания которых дают распределение напряжений, удовлетворяющих на границе заданным силам. Первый способ лишен этой особенности, т. к. в нем массовые силы входят в состав заданных условий и задача состоит только в отыскании поля перемещений.

Обсуждение и заключения. Второй способ решения задачи обладает наилучшей сходимостью. Кроме того, в отличие от первого способа при вычислении скалярных произведений в процессе ортогонализации и при определении коэффициентов Фурье, во втором способе не используются деформации и перемещения. Здесь формируется базисный набор напряжений и его след на границе ― базисный набор поверхностных сил, с помощью которых проводится ортогонализация и построение рядов. Это означает, что при вычислении скалярных произведений не возникает погрешность, связанная с составляющими, отвечающими за жесткое перемещение, которое может возникать при формировании базиса [11].

Механика

Если рассматриваются задачи с массовыми силами, то второй способ может оказаться полезным при формировании множества частных решений, напряжения которых удовлетворяют определенным условиям на границе. Эти решения могут быть использованы в качестве базисных в более сложной задаче, а также быть полезными при определении упругих полей, реализуемых от фиктивных нагрузок, возникающих в результате применения метода Пуанкаре [7, 8].

Проанализирована точность решения задач теории упругости методом граничных состояний при использовании разных подходов в построении скалярных произведений. Решение задачи линейной теории упругости, использующее представление общего решения уравнения Ламе в виде ряда Фурье по базисным функциям и выражение (6) в качестве ортогонализатора этих функций, имело наилучшую сходимость.