Движение экипажа на упругих колесах

При движении жесткого колеса по жесткой опорной поверхности под действием силы, направленной под некоторым углом к плоскости колеса, увод практически незаметен, при качении же обрезиненного колеса или, более того, колеса с пневмошиной увод становится значительным. Что касается бокового увода колеса, или поперечного упругого скольжения, то его можно реально наблюдать на колесных транспортных средствах.

Рассмотрим автомобиль, у которого управляющие упругие колеса находятся под некоторым углом, и проследим, в каком направлении будет двигаться колесо, когда на него действует сила тяги F . Очевидно, что направление действия силы и плоскость колеса не совпадают. Существуют различные варианты [1, 6] учета этого явления при практических расчетах, но все они обладают одним существенным недостатком: они не позволяют решать обратную задачу – как по известному направлению качения колеса определить направление и величину действующей на него силы. Использование функции нагружения колеса [ 4, 5 ] позволяет решать как прямую, так и обратную задачи. Необходимо лишь подобрать такую форму функции нагружения f , чтобы нормаль к ней в каждой точке приложения силы соответствовала направлению качения колеса. При этом следует отметить, что функция нагружения колеса должна удовлетворять некоторому требованию: она должна быть невогнутой, что объясняется необходимостью обеспечения принципа максимума скорости диссипации механической работы [3]. Можно показать, что из этого условия вытекает необходимость направления скорости движения колеса строго по нормали к линии

нагружения. В противном случае движение колеса будет неустойчивым: при отклонении действующей на колесо силы в одном направлении направление скорости движения колеса может отклоняться в другом направлении. Однако важным является необходимость учета того, что направления действующей силы и скорости движения колеса могут не совпадать.

В каждом конкретном случае может быть использован свой способ учета расхождения направления действия силы и направления качения колеса: например, сама функция нагружения может быть представлена в виде эллипса, или при достижении силой F какого-либо участка границы функции нагружения f отклонение направления качения колеса от нормали в каждой точке может быть представлено [2, 3, 5] в виде некоторой функции а = а (f, F, е). (1)

Эта зависимость определяет, в каком направлении будет двигаться колесо, имеющее функцию нагружения f и подвергающееся воздействию силы F , направленной под углом е к плоскости колеса. Эта же зависимость позволит при решении обратной задачи находить направление и величину действия силы при известном направлении качения колеса.

На рис. 1 показано, что качение абсолютно жесткого колеса по абсолютно жесткой поверхности начинается с момента, когда величина вектора силы F достигает прямолинейного участка линии нагружения и становится равной Fi. При этом значение составляющей Fхi становится равным силе сопротивления движению Fс в плоскости колеса (качению), а составляющая Fуi вызывает увод колеса, и величина увода (угол аi отклонения вектора скорости движения vi от плоскости колеса) будет зависеть именно от величины Fуi [1, 2, 4, 6]. Действительно, под действием нагрузки Fi, направленной под некоторым углом ei к плоскости колеса, вектор скорости движения колеса vi отклоняется от нормали к первоначальной линии нагружения на угол ai и образует с вектором силы Fi угол

Ф . = £ i - a t .              (2)

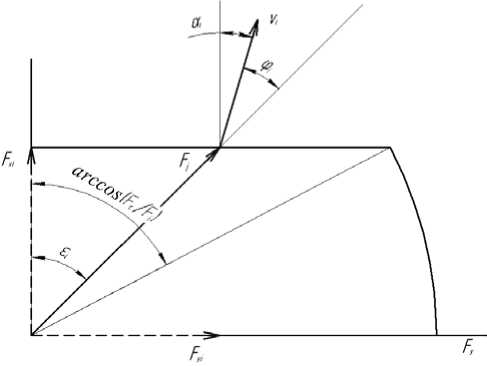
Рис. 1. Отклонение вектора скорости движения колеса с уводом от направления действия силы

При отклонении вектора скорости vi от нормали к функции нагружения колеса нарушается условие перпендикулярности вектора скорости к «первоначальной» функции нагружения, которую имеет колесо до начала действия силы. Однако функция нагружения в процессе нагружения колеса некоторой силой [2-4] обладает свойством изменять свое положение, поэтому при достижении прикладываемой к колесу силой некоторой величины (вектор силы достигнет линии нагружения) функция нагружения в этой точке совершает поворот на угол a , равный величине угла отклонения вектора скорости от нормали к первоначальной линии нагружения. В результате вектор скорости движения колеса станет перпендикулярным к этой «новой» линии нагружения (рис. 2). Сила сопротивления качению станет равной F_cx , которая и определяет скорость движения колеса. Сила F_cy определяет величину угла а отклонения вектора скорости от нормали к исходной функции нагружения. На рис. 2 видно, что сопротивление качению F c _K оказывается несколько больше, чем при качении в плоскости колеса F_xo . Таким образом, при действии на колесо некоторой силы по известной из эксперимента зависимости (1) можно всегда рассчитать направление движения колеса. Кроме того, такой подход позволяет решать и обратную задачу: как по известному принудительному движению колеса определить величину и направление действующей на колесо силы.

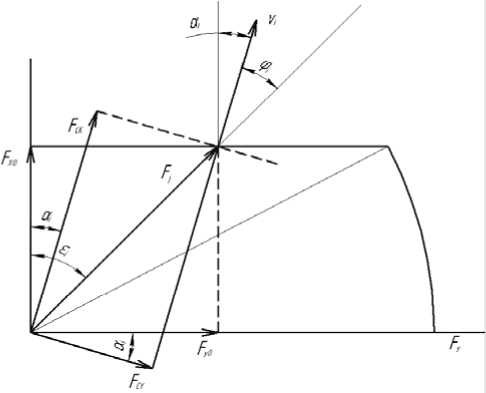
Рис. 2. Изменение функции нагружения при качении колеса с уводом под действием силы, направленной под углом к плоскости колеса

Аналогично пространству сил введем пространство скоростей движения колеса экипажа С^р, в котором прямоугольные координаты рассматриваемой точки равны компонентам вектора скорости v p . Это означает, что каждому значению вектора v^p в пространстве С^р соответствует некоторая точка или радиус-вектор v^p , которая некоторую линию равного уровня, называемую в математической теории пластичности диссипативной функцией. Тогда по аналогии с функцией нагружения соответствующая скорости сила, действующая на колесо, должна быть направлена по нормали к этой линии.

Таким образом, рассмотренная модель движения колеса может быть введена двумя эквивалентными путями: или через определение функции нагружения, или через определение диссипативной функции. При этом в обоих случаях необходимо формулировать принцип максимума. Использование функции нагружения позволяет описать анизотропные свойства колеса. Это можно сделать, если в пространстве сил каждой фиксированной функции нагружения поставить в соответствие функцию анизотропии [3], являющуюся годографом вектора сил относительно вектора скорости (нормали) в соответствующей точке линии нагружения (рис. 3). При построении линии анизотропии вектор F откладывается от фиксированной оси ОО 1 в направлении, которое он образует с вектором скорости (нормалью) в данной точке линии нагружения. Очевидно, что для круглой изотропной функции нагружения замкнутая линия стягивается в точку на расстоянии F от начала отсчета на оси ОО 1 .

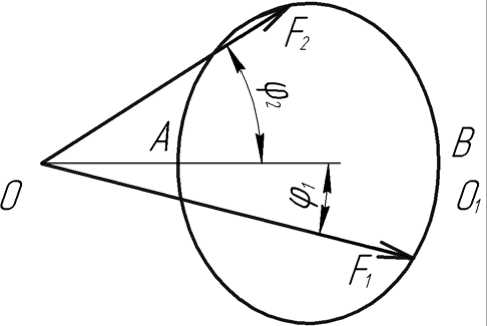
Рис. 3. Построение функции анизотропии

Необходимо заметить, что линию анизотропии можно построить для разных уровней диссипативной функции. Для устойчивых систем отрезок АВ (рис. 3) будет увеличиваться, причем точки А и В будут двигаться в противоположных направлениях, для неустойчивых систем отрезок АВ будет изменяться, при этом точки А и В будут двигаться в одном направлении. Угол отклонения вектора скорости от вектора силы в точке, принадлежащей функции нагружения, показывает, что колесо двигается в направлении скорости v, а возникающие при этом силы сопротивления Fx и бокового увода Fy и составляющие в сумме результирующую силу F , представляют собой динамическую характеристику колеса. Тогда построенную функцию анизотропии можно считать по аналогии с крылом полярой колеса, которая показывает зависимость величины действующей на колесо силы F от угла отклонения плоскости колеса от направления его движения (сравним с углом атаки крыла) или иначе соотношение сил сопротивления Fx и сил увода Fу (подъемной силы крыла в аэрогидродинамике). Зная зависимость (1), можно определить зависимость ε = ε(α), затем по известному направлению действующей на колесо силы – рассчитать величину вектора силы как расстояние от начала координат до границы функции нагружения f.

Выводы:

• 1.    На основе сделанных предположений и допущений сформулирован новый класс моделей движения колеса, который позволяет описывать поведение колеса и определять параметры его движения при различных условиях нагружения.

• 2.    Построена функция нагружения колеса, которая, являясь важнейшей характеристикой его механических свойств, однозначно определяет направление его движения. Установлено, что вектор скорости движения колеса не всегда совпадает с направлением действия силы и должен быть направлен по нормали к функции нагружения.

• 3.    Построена поляра колеса, характеризующая его анизотропность.