Движение космического аппарата с тросовой системой при нештатных ситуациях
Автор: Дюков Д.И.
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Механика и машиностроение
Статья в выпуске: 4-1 т.12, 2010 года.
Бесплатный доступ
Исследуется движение космического аппарата с тросовой системой, предназначенной для доставки груза на Землю, при нештатных ситуациях. В работе рассматривается нештатная ситуация - столкновение груза с несущем космическим аппаратом (КА) вследствие заклинивания троса. Движение груза после заклинивания обусловлено силой упругости троса, и скорость обратного движения груза определяется согласно ударной теории с помощью коэффициента восстановления. Получены уравнения движения тросовой системы с грузом и проведен анализ возвратного движения груза. Моделирование проводилось при различных значениях коэффициента восстановления, определено граничное значение коэффициента восстановления, при котором соударение не происходило. Результаты могут быть полезными при выборе характеристик троса и его геометрических конфигураций, уменьшающих коэффициент восстановления, например, разрывные петли.
Космический аппарат, тросовая система, нештатная ситуация, коэффициент восстановления троса
Короткий адрес: https://sciup.org/148199372
IDR: 148199372 | УДК: 629.78
Текст научной статьи Движение космического аппарата с тросовой системой при нештатных ситуациях
Космическая тросовая система (КТС) представляет собой комплекс искусственных косми-че-ских объектов соединённых длинными тонкими гибкими элемен-тами совершающий орбитальный полет. КТС можно использовать для доставки грузов с орбиты на поверхность Земли. Для обеспечения приземления в заданный район необходимо весьма точно провести маневр спуска с орбиты, требующий развертывания троса и отсоединения груза от троса [1, 2]. Смысл транспортной операции с использованием КТС можно описать следующим образом [3]. С космического аппарата (КА) на гибком тросе в вертикальном направлении с некоторой скоростью выпускается груз. Под действием кориолисовой силы груз отклоняется от местной вертикали в сторону направления движения спутника. По мере увеличения длины троса высота груза над поверхностью Земли будет уменьшаться, а гравитационное ускорение, действующее на груз, будет увеличиваться по сравнению с аналогичным ускорением, действующим на спутник, за счет этого груз совершит возвратное движение в направлении вертикали спутника. Находясь в окрестности этой вертикали, груз будет иметь скорость меньшую, чем скорость спутника. Другими словами, за счет возвратного движения груз получит отрицательное приращение к орбитальной скорости, эквивалентное тормозному импульсу. С дру-
гой стороны, первая космическая скорость V I . r r2 на высоте груза больше, чем на высоте спутника. Если на этом этапе разорвать трос, то груз по баллистической траектории совершит спуск в атмосферу. Операция доставки груза с орбиты является одной из многих задач в программе проводимых исследований в течение полета космического аппарата, поэтому проблемы, связанные с работой тросовой системы, не должны препятствовать выполнению других задач. Важно предусмотреть возможность возникновения нештатной ситуации, выявить ее на ранней стадии и вовремя принять все необходимые меры для ее устранения (вплоть до обрыва троса и потери груза). Нештатные ситуации можно условно разделить на две группы: опасные для груза и опасные для груза и КА [3]. К первой группе можно отнести сбои в работе космической тросовой системы, при которых доставка груза на Землю невозможна. Ко второй группе относятся нештатные ситуации, приводящие к столкновению КА и груза. Это может повлечь за собой поломку антенн, солнечных батарей и другого внешнего оборудования КА.
Целью работы являлось рассмотрение нештатной ситуации – заклинивание троса в процессе развертывание. Для этого получены уравнения движения КА с тросовой системой и грузом, проведено моделирования заклинивания троса в соответствии с элементарной теории удара для различных коэффициентов восстановления троса и выполнен анализ полученных результатов.
УРАВНЕНИЯ ДВИЖЕНИЯ КА С ТРОСОМ
В качестве модели будем использовать систему, состоящую из двух объектов (КА и груза), значительно различающихся по массе и соединенных между собой тросом. КА совершает движение по круговой орбите Земли. Сила натяжения троса T изменяется по известному закону [4]. Массой троса будем пренебре гат ь. Введем систему координат O 1 xy . В ект ор O 1 x направлен в сторону движения КА, O 1 y - к центру Земли. В точке O 1 располагается центр масс КА, в точке A – груз, точка O является центром Земли (рис. 1).
Известно несколько моделей КТС. Для проведения исследований будем использовать уравнения, описывающие движение КА в случае невесомого, упругого и тонкого троса [1]:
е mV = - X - mg sin 0 + T cos(0 + ф), ния r0 – начальное положение тела O1 , г0 = гз + h0 и Г1 - текущее положение тела O1, Г1 = гз + h где гз - радиус Земли.
Уравнение движения точки A относительно центра O 1 имеет вид [5]: ■ ■ ^^^^ ^^^^ ^^^^ ^^^^ ^^^^
Ш а Р = m A g + T + Ф е + Ф к + X a = Ф 0 , (2) где XA – сила аэродинамического сопротивления, действующ а я на точку A , T – сила натяжения троса, m g - с ила тяжести, Фe – переносная сила инерции, Фk – кориолисова сила инерции, р = OA (рис. 1.).
Рассмотрим переносную силу ине р ции Фе = — mW e , где переносное ускорение W e вычисляется по формуле [6] We = W - Ор + £ х р , где £ = О . Поскольку O 1 x 1 — 1 левосторонняя система координат и учитывая, что mAW = mAg + T + XA , то окончательное выражение для W можно записать так:
V mV 0 --cos 0
•
■ h = V sin 0,
l = r0 v cos 0 , r 1
= - mg cos 0 - T sin( 0 + ф ),
W = -( T + X a ) + g. (3)
m
g Кориолисова_сила инерции имеет вид Фк = - mW k , где W k = 2 О х р . Запишем выражение для углового ускорения £ = О . Опуская подробные выводы и учитывая, что Г = h & = v sin 0 , можно записать выражение
где T – сила натяжения троса, X – сила аэродинамического сопротивления, 0 - угол наклона траектории, ф — угол в плоскости орбиты, g -сила тяжести, m – масса центра масс КА, mA – масса груза, V – скорость движение КА, h – высота полета, l – дальность полета.
Для дальнейших исследований получим уравнения движения груза относительно КА. Связанная с КА система O 1 xy вращается с угло-
V вой скоростью о = — cos 0. Введем обозначе-
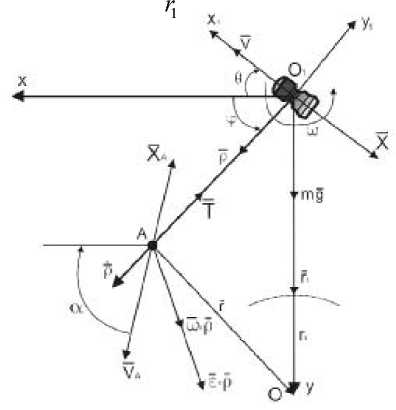
Рис. 1. Движение КА с тросовой системой и грузом
V V VO . V v 2
£ = —cos0--sin 0---sin 0 cos 0 и при- r1 r1 r12
ближенно можно считать, что
■
V
— cos 0
r 1
Для получения окончательной системы уравнений КА с тросовой системой и уравнений движения груза относительно КА воспользуемся уравнениями движения двух тел на орбите Земли [5]:
1 xR x = 2«y--T —l—-, mA P mA y = 3o2y - 2rnx —— T — +—-, (5)
mA P mA где Rx , Ry – составляющие силы аэродинамического сопротивления, x,y – координаты вектора р в системе координат O1 xy . В уравнения относительного движения тел на орбите (5) надо добавить новые слагаемые из формул (3), (4). Выпишем отдельно новые члены для уравнения (2):
т р = Ф 0 +Д Ф . (6)
Рассмотрим второе слагаемое в правой части дифференциального уравнения (6):
А Ф — - m A e x p - m A ( T + X ) . (7)
m
Проецируя равенство (7) на оси O 1 x и O 1 y
xy и, учитывая, что cos ф — — и sin ф — — , запи-Р Р шем с учетом (5) уравнения движения:
Системы (1) и (10) представляют полную систему уравнений движения КА с тросовой системой и уравнений движения груза относительно КА. На основании этих уравнений будем проводить все дальнейшие исследования по изучению нештатных ситуаций.
НЕШТАТНЫЕ СИТУАЦИИ
x — 2toy + ey -
— + -1 Tx+-X cos#, V mA m J p m
y — 3to2y - 2rax - ex -
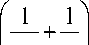
Ty - - X sin # ,
V m m j
p m
Теперь к этим уравнениям необходимо добавить аэродинамическую силу XA , действующую на груз A . Выражение для абсолютной скорости груза запишем в виде: V A — V + р + ® х р .
Сила X A — Cx A
p V 2 v
2 A
направлена в сторо-
ну, противоположную направлению VA . К уравнениям (8) необходимо добавить
Рассмотрим нештатные ситуации, связанные со столкновением груза с КА вследствие заклинивания троса. Движение груза после заклинивания обусловлено силой упругости троса, и скорость обратного движения груза определяется согласно ударной теории груза с помощью коэффициента восстановления k . Изменение скорости тел при ударе зависит от упругих свойств соударяющихся тел. Эти свойства при ударе характеризуются величиной, называемой коэффициентом восстановления. Величина k , равная отношению модуля скорости u в конце удара к модулю скорости в начале V называется коэф-
АФ X — —— X. cos a „ АФ x — —— X. sin a xA и yA mA и mA
В результате получим:
фициентом восстановления k — u^ . Этот коэф-
x—toy+ey -
'2
V m A
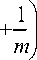
x 1 1
T— +— Xcos#--XA cosa, p m mA
V m A
y—3toy-tox-ex -
А1 m J
T— —- X sin #—- XA sin a p m m A
Систему (9) можно упростить, учитывая допущение о том, что скорость развертывания троса
p
>
не превышает начальной скорости отделения тела
A
от космического аппарата и много меньше скорости
V
, а масса груза много меньше массы КА, то есть
m
A
<
V Р
to- р — — pcos# — V cos #—<< 1.
r 1 r 1
При выполнении вышесказанных допущений сила XA имеет одинаковое направление с X , а V A — V . Таким образом, движение груза относительно КА описывается в виде:
1 х
X — 2 to y + ey--T- +
m p
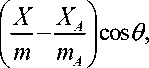
y — 3 to 2 y - 2 to X - e x —TT— m p
-
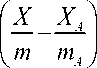
sin #.
фициент не зависит ни от размеров тел, ни от их относительной скорости, а определяется только свойствами их материала и его значение лежит в пределах 0 < k < 1 . Для анализа движения проведем моделирование при различных коэффициентах восстановления k . Непосредственное моделирование нештатной ситуации проводится следующим образом: на некоторой стадии развертывания происходит заклинивание, после чего интегрирование системы проводится со скоростью, направленной в обратную сторону, и умноженную на коэффициент восстановления. На рис. 2, 3, 4 показаны результаты моделирования. Видно, что после заклинивания груз начинает двигаться в противоположном направлении, то есть в сторону КА. Рис. 2 показывает, что при коэффициенте восстановления к — 0,5 соударение не происходит даже на 10 секунде после начала развертывания. На рис. 5 показана зависимость расстояния от оси y до точки соударения груза и нижней границей КА с момента заклинивания для разных значений коэффициента восстановления. Сравнивая полученные результаты (рис. 5), видно, что заклинивание наиболее опасно, если оно произошло до 50 секунды после начала развертывания, так как при этом наиболее вероятно соударение груза с корпусом КА.
Заключение. В статье рассмотрены нештатные ситуации, возникающие при развертывании космической тросовой системы, и проведен анализ нештатной ситуации заклинивания троса. По результату проведённого анализа можно сделать вы-
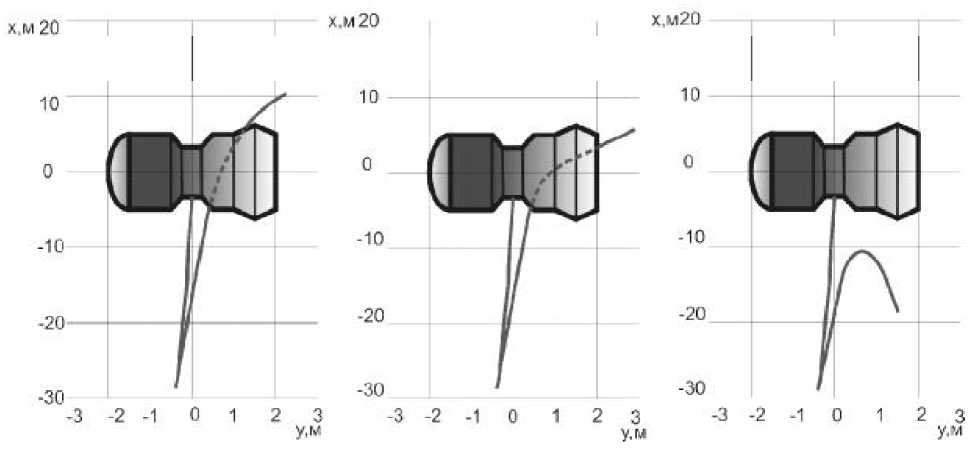
Рис. 2. Заклинивание троса на 10 секунде при k = 1; 0,8; 0,5
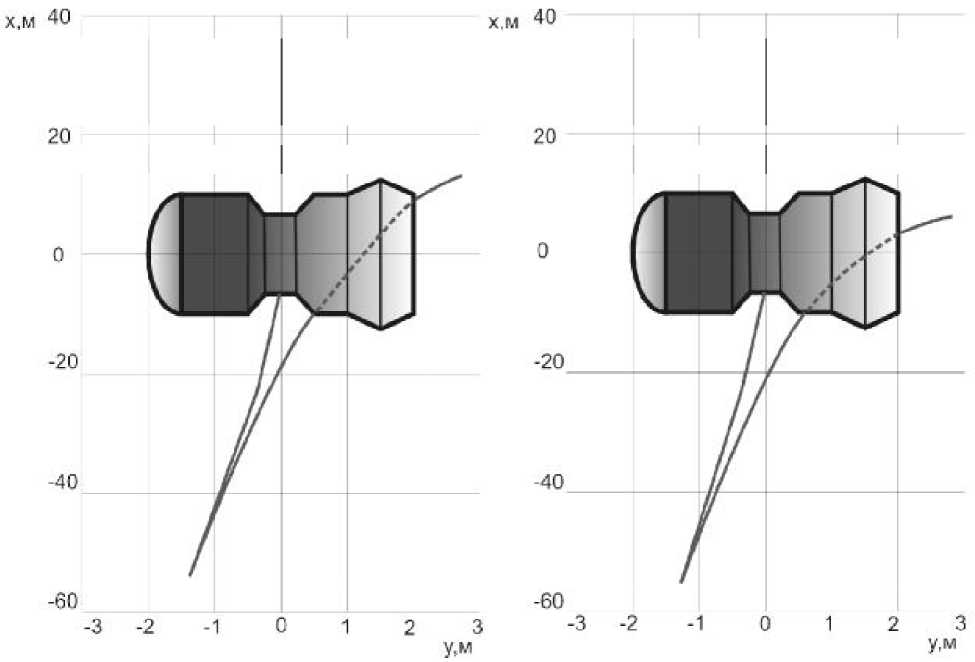
Рис. 3. Заклинивание троса на 20 секунде при k = 1; 0,8
вод, что заклинивание особенно опасно на начальном этапе развертывания. Пограничное значение коэффициента восстановления при котором соударение не происходит k = 0,63 . Очевидно, что для снижения вероятности соударения груза с КА в случае нештатной ситуации необходимо уменьшать коэффициент восстановления k различными конструктивными методами, например, с использованием тросов с разрывными петлями.
Автор выражает благодарность профессору Асланову В.С. за постановку задачи и постоянное внимание к работе.
Работа выполнена при поддержке Российского фонда фундаментальных исследований (09-01-00384а).
Список литературы Движение космического аппарата с тросовой системой при нештатных ситуациях
- Белецкий В.В., Левин Е.М. Динамика космических тросовых систем. М.: Наука, 1990. 329 с.
- Сидоров, И.М. Об использовании тросовых систем для создания постоянно действующего транспортного канала в космическом пространстве//Полет. 2000. №8. С. 36-39.
- Асланов В.С., Ледков А.С., Стратилатов Н.Р. Пространственное движение космической тросовой системы, предназначенной для доставки груза на Землю//Полет. 2007. №2. -С. 28-33.
- Zimmermann F., Schottle U., Messerschmid E. Optimization of the tether assisted return mission of a guided re entry capsule//Aerospace Science and Technology. 2005. V. 9. №8. P. 713 721.
- Добронравов В.В., Никитин Н.Н. Курс теоретической механики. М.: Высш. школа, 1983. 575 с.
- Маркеев А.П. Теоретическая механика: Учебник для университетов. Ижевск: НИЦ "Регулярная и хаотическая динамика", 2001. 592 с.


