Движение в атмосфере тросовой системы спускаемый аппарат - аэродинамический стабилизатор

Самарский государственный аэрокосмический университет

Рассматривается движение в атмосфере спускаемого аппарата с прикрепленным к нему на тросе аэродинамическим стабилизатором. Получены уравнения движения данной тросовой системы, которые представляют собой систему обыкновенных дифференциальных уравнений в неявной форме. Построенная математическая модель состоит из уравнений вращательного движения обоих тел и уравнений, учитывающих механическую связь между ними в виде прямолинейного невесомого троса. Найдены условия статической устойчивости движения в атмосфере рассматриваемой механической системы. Проведен анализ влияния на устойчивость движения в атмосфере изменения параметров аэродинамического стабилизатора и длины троса.

Постановка задачи

В настоящее время в космонавтике все большую популярность приобретают различные тросовые системы [1], применение которых расширяет возможности управления движением космических аппаратов (КА). В данной работе рассматривается движение в атмосфере тросовой системы спускаемый аппарат (СА) – аэродинамический стабилизатор (АС). Подобные тросовые системы могут быть использованы для аэродинамической стабилизации движения КА на различных участках его полета: на низких орбитах движения вокруг Земли или других планет [2], имеющих атмосферу; в верхних слоях атмосферы (на высотах 100-200 км) для предварительной стабилизации движения перед спуском; в плотных слоях атмосферы для обеспечения устойчивого движения перед приземлением вместо парашютной системы. В настоящее время прорабатывается также возможность применения таких механических систем для стабилизации движения отделяемых ступеней и боковых блоков ракет-носителей для уменьшения районов их возможного падения. Применение аэродинамического стабилизатора на тросе позволит уменьшить требования к точности изготовления спускаемого тела, так как выбором длины троса можно обеспечить практически любой запас статической устойчивости механической системы.

При построении математической модели тросовой системы СА – АС два концевых тела рассматриваются не как материальные точки, как это обычно делается при моделировании тросовых систем [1], а как твердые тела, для которых записываются уравнения их вращательного движения. Данный подход позволяет проводить анализ не только задачи ориентации троса по отношению к набегающему потоку воздуха, но и комплексный анализ устойчивости всей механической системы с учетом вращательного движения концевых тел по отношению к вектору скорости.

Уравнения движения механической системы

Рассмотрим вывод динамических уравнений движения связки двух твердых тел на тросе, описывающих их вращательное движение в атмосфере. На любое твердое тело в атмосфере действуют аэродинамическая (R ) и гравитационная (G ) силы. Обычно при получении уравнений вращательного движения твердых тел в атмосфере гравитационным моментом пренебрегают вследствие его малости относительно аэродинамического момента M . Равнодействующие аэродинамических сил каждого тела приложены в центрах давления, положения которых определяется заданными аэродинамическими характеристиками СА и АС. При выводе уравнений движения механи- ческой системы будем считать трос невесомым, рассматривая его как геометрическую связь между телами системы.

На рис. 1 изображена рассматриваемая механическая система. Помимо аэродинамических и гравитационных сил на СА и АС действуют силы натяжения троса N и N ‘ , причем N = - N ‘ . Величины, относящиеся к СА, АС и тросу обозначаются индексами 1, 2 и 3 соответственно. Тела, составляющие рассматриваемую механическую систему, по форме близки к осесимметричным телам.

Динамические уравнения движения каждого тела запишем, используя теорему об изменении кинетического момента

——        —— где K1 и K2 – кинетические моменты тел,

M AR )=A — х R

и M C 2 ( ^2 ) =А —

——

х R 2

——

– моменты аэродинамических сил R ₁ и R ₂ ,

MC (TN)= —1 х N и MC (TN‘)= r2 х TN' -

~ ^— dK ₁

dt

+ 0 1 х K 1

= Ml с,(Ri)+ Ml с,(N),

~ ^— dK ₂

dt

+ 0 2 х K 2

= M l C 2 (^2 ) + M l C 2 ( N ') , (2)

моменты силы натяжения троса, А — и A r ₂ – вектора положения центров давления аэродинамических сил относительно цен-трое масс каждого тела (рис 1), — и r ₂ -вектора, определяющие положение точек крепления троса относительно центра масс каждого тела, 0 1 и О ₂ - угловые скорости

~ —   ~ — dK1   dK2

вращения СА и АС, 1 и 2 – локаль-dt dt ные производные.

Для определения силы натяжения троса

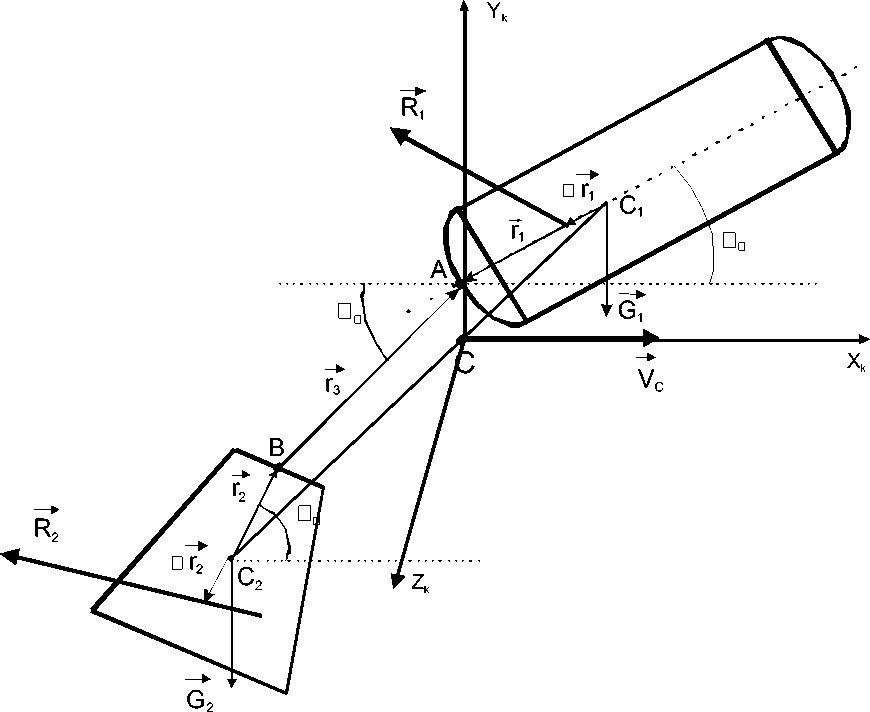
Рис. 1. Механическая система спускаемый аппарат – аэродинамический стабилизатор

N запишем теорему о движении центра масс спускаемого аппарата и всей механической системы

d 2 r1C где W1C    dt2

– ускорение центра масс С А

относительно центра масс системы,

« 1—1 = N + R + G 1 ,       (3)

dt

dV

( m_x + m ₂)---- = R + R ₂ + G , + G (4)

1       2 dt 1       2       1

где G 1 = m 1 g 1 и G ₂ = m 2 g 2 - гравитационные силы, действующие на СА и АС соответственно, V_C – скорость центра масс системы, V_{C 1} – скорость центра масс СА относительно центра масс системы, V 1 = V C + V C 1 - скорость центра масс СА, m 1 и m ₂ - массы СА и АС, g 1 и g 2 - гравитационные ускорения.

Определяя силу N из уравнения (3) и

i C = m + m C 1 C 2 - вектор, соединяющий

центр масс системы и центр масс СА, C ₁ C ₂ – вектор, соединяющий центры масс СА и АС.

Определим значение ускорения W _{1 C} , продифференцировав вектор r _x C , тогда

—   d2 rxr      m,d

1C               21 2

1C —    2 —2

dt      m 1 + m 2

Выражая вектор C 1 C 2 через вектора r 1 ,

r ₂ и r ₃ (рис.1), найдем

вычисляя скорость V ₁ через скорость центра масс системы, получим

W

W _{1 C}

m ₂

m 1 + m ₂

d ² r d ² r d ² r

—Л — т +—Л dt ² dt ²     dt ²

. (8)

N = m,  V + т,  **' - R. - G.     (5)

¹   dt ¹    dt ^{1      1 .     (5)}

Подставляя уравнение (4) в выражение (5), найдем

Таким образом, выражение для силы натяжения троса (7) примет следующий окончательный вид

N

N = —m— G ₂

m1 + m ₂

—m 2— G +.

m1 + m ₂

mm

=---1— R 2--2— R1 + m1 + m 2     m1 + m 2

⁺ m ^{1   (} R i ^{+ R} 2 ^{)- R} 1 ⁺ m i dV C ¹ . (6)

m 1 + m ₂                       dt ^v ’

mm

+ — m1 + m 2

f J 2 i

I ddt?

J 2 ^ J 2 ^ Л drxdr

----1 +- dt2

Если пренебречь изменением гравитационного ускорения в пределах механической

Причем производные векторов r _1,2,3 оп-

r r r           i системы, то g 1 = g2 = g , G1 = m1 g ,

ределяются в системах координат, связанных с каждым из трех тел системы по правилу дифференцирования векторов в подвижных системах координат

^G 2 = m 2 ^g и

m¹  G ₂-- m^- G 1 « 0

m 1 + m ₂       m 1 + m ₂        ^.

d ² Г , dt ²

= i x r + (У_x x (x x rⁱ_i ) , i = 1,2,3 ,

r r где ω и ω – угловая скорость и угловое ус-

С учетом этого допущения формула (6) примет окончательный вид

N

—m— R 2--m2— R1 + m1W1 C m1 + m 2     m1 + m 2           ’

корение каждого тела.

Сила натяжения троса совпадает по направлению с вектором r ₃ . В этом случае про-

екции силы натяжения троса на оси системы

координат, связанной с тросом y ₃ и z ₃ рав-

ны нулю. Поэтому Ny₃ = 0, Nz₃ = 0. Эти условия фактически представляют собой уравнения связи, которые запишутся в виде

N y 3

m 1            m 2

-----,-----R 2 у 3--,-----R1 у 3 + m1 + m 2       m1 + m 2

mm

+ — m ₁ + m ₂

•

f -

^ tv

—

d ² r,

—Л + dt2

d ² r ₃ dt ²

\

^J у 3

= 0. (11)

N

z 3

m 1

R 2 z 3

m 1 + m 2

—

m 2

R 1 z 3

m 1 + m ₂

+

m ^m 2 / dr _— d i r t ₊ dr'

m 1 + m 2 ( dt ²     dt ²     dt ² J z 3

= 0. (12)

К уравнениям (11-12) необходимо присоединить динамические уравнения вращательного движения каждого тела (1-2), которые удобнее записать в главных связанных системах координат. Тогда K i = J i m i , где

i = 1,2 , J i - диагональные матрицы моментов инерции СА и АС.

Проецируя динамические уравнения (12) на оси главных связанных систем координат каждого тела, группируя в левых частях каждого из уравнений системы (1), (2), (11), (12) слагаемые с множителями d i и перенося в правую часть другие слагаемые, получим следующую систему динамических уравнений, описывающих вращательное движение механической системы в матричной форме dω

A • s⁼B •         ⁽¹³⁾

где A = ^[ 4 , 1 - матрица переменных коэффициентов, зависящих от углового положения и угловых скоростей каждого тела, to = I d , d, , d • ^юх • ^tov • ^to _z , rn_v , d Г — x ₁ y ₁ z ₁ x ₂ y ₂ z ₂ y ₃ z ₃ вектор компонент угловых ускорений, B =^[ B j J – вектор правых частей дифференциальных уравнений. Формулы для компонент матриц A и B вследствие их громоздкости в данной статье не приводятся.

Полученные динамические уравнения

(13) необходимо дополнить кинематическими уравнениями, например, уравнениями Эйлера для двух тел и троса, и уравнениями движения центра масс, которые записываются в традиционной форме.

Если рассмотреть идеальный невозмущенный случай движения связки двух симметричных сферических тел со смещенным центром масс при постоянном скоростном напоре q = const , то в этом случае полученная система уравнений будет иметь четыре первых интеграла движения: интеграл энергии вращательного движения системы, интеграл проекции кинетического момента на вектор скорости V_c и интегралы проекций угловых скоростей (5 1 и ( 5 ₂ на оси симметрии x 1 и x ₂ каждого тела. Причем последние дв а интеграла существуют и для симметричных вытянутых тел. Перечисленные первые интегралы движения системы были использованы для тестирования полученной математической модели при проведении численных расчетов на компьютере, которые подтвердили существование данных интегралов движения.

Определение статических условий устойчивости движения механической системы

Рассмотрим плоское движение связки СА – АС. Плоская задача получается как частный случай пространственного движения при нулевых угловых скоростях вращения ro xi = 0, где i = 1,2,3. Необходимость рассмотрения плоской задачи связана с записью условий статической устойчивости движения системы в атмосфере, а именно, статической устойчивости частного решения a i = 0 ( i = 1,2,3.). В классической задаче движения СА в атмосфере условие статической устойчивости записывается достаточно просто: центр масс должен быть смещен по отношению к центру давления равнодействующей аэродинамической силы вперед в сторону лобовой части (носка) аппарата. Причем известно, что переход к пространственному случаю движения (учет гироскопических чле-

нов) не может разрушить устойчивости движения механических систем [3]. Поэтому при рассмотрении задачи об устойчивости движения системы СА и АС в атмосфере в первую очередь необходимо получить условия статической устойчивости движения системы. Статические условия устойчивости по-ложенияравновесия a i = 0 ( i = 1,2,3.) системы являются необходимыми условиями устойчивости движения системы СА и АС в атмосфере. С другой стороны наряду со статическими условиями при движении тел в атмосфере рассматриваются также динамические условия устойчивости, которые определяют медленное уменьшение амплитуд колебаний переменных относительно рассматриваемого невозмущенного решения а = 0 ( i = 1,2,3.). Эти условия можно рассматривать как достаточные условия устойчивости положения равновесия системы. Выполнение достаточных условий устойчивости обычно определяется действием на систему различных возмущений (медленное изменение параметров системы, действие диссипативных слагаемых и т. д.).

Для получения условий статической устойчивости системы рассмотрим малые колебания механической системы относительно положения равновесия a ₁ = a ₂ = a 3 = 0 . Тогда, полагая sin a i * a i , cos a i * 1, a i = m i ( i = 1,2,3) и пренебрегая нелинейными слагаемыми, из системы (13) получим

(

C =

— A R x r —

—

—

к

m ₂ r ₁

m 1 + m 2

m ₂ r ₂

m 1 + m ₂ m ₂

m 1 + m 2

^R 1 ^αyk

^R 1 ^αyk

^R 1 ^αyk

—

m ₁ r ₁

m ₁ + m.

A R x r 2 +

R2αyk m1r2  R

m 1 + m 2

m ₁

m 1 + m 2

^R 2 ^αyk

α

2 yk

—

Здесь

D =

Da + Ca = 0.

⁽ J 1 + m 12 r 12 m 12 r 1 1

I      ^m 12 ^r 1

a =

^a 1

α ₂

к ^a 3 J

,

m 12 r 1 l

J 2 + m 12 r 2

m ₁₂ r ₂

m 12 r 1 r 3

m 12 r 2 r 3

m 12 r 3 _v

к

,

A R x J

J ₁ и J ₂ – моменты инерции СА и АС относительно поперечных осей, r = AC 1 ,

l = BC ₂, L = AB (рис.1), ^m12

m ₁ m ₂

m 1 + m ₂ ’

R '. = ( C x 1 + C y 1 ) qS 1 , R ayk = ( C x 2 + C y 2 ) qS 2 ,

S ₁ и S ₂ - характерные площади СА и АС, C_xi и C_yi ( i = 1,2) - коэффициенты аэродинамических сил в связанных системах координат,

A R x

m 1 ^R 2 xk ^— m 2 ^R 1 xk

m 1 + m ₂

R xk и R yk ( i = 1,2) —

проекции аэродинамических сил СА и АС на оси траекторной системы координат

CX_kY_kZ_k (рис.1), R_i ^α _yk - частные производные

коэффициентов по углу атаки α_i .

Анализ статической устойчивости сводится к анализу корней характеристического уравнения динамической системы (14), которое имеет вид

det ( Dx ² + C ) = 0.         (15)

Раскрывая определитель и приводя подобные слагаемые, получим кубическое относительно λ2 уравнение px + qx' + rxX" + tx = 0.    (16)

Здесь

P x = m 12 1 1 1 2 r 3 ,

4 x = ^— [ ^m 12 ¹ 1 ^r 2 ^{( r} 2 ^{+ r} 3 ^{)+ m} 12 ¹ 2 ^r 1 ^{( r} 1 ^{+ r} 3 ^{)+ 1} 1 ¹ 2^{] A R} x ,

(                                                                         \                                 (                                                                       1

r, = I A R,r d A R,-- ¹   ■ R“ 1 + 1 ₂ A R,r ,l A R , +----2— ■ R“ 1 +

λ 1 x 2 x                    2 yk       2 x 1 x                    1 yk

I ^m 1 ^{+ m} 2 J         I ^m 1 ^{+ m} 2      J

^{+ m} 12 ^{A R2 r} 1 ^{( r} 1 ^r 2 ^{+ r} 22 ^{+ r} 2 ^r 3 J i

t x =— r 1 r 2 ( a r x ) ² ■(a r x —A R y ) ,

где ^{A R}y

m 1^R 2 yk ^— m 2 ^R 1 yk

m 1 + m ₂

Решение а 1 = а 2 = а ₃ = 0 будет статически устойчиво, если корни характеристического уравнения будут все чисто мнимыми, а это будет выполнено тогда и только тогда, когда кубическое уравнение (16) относительно λ ² будет иметь три вещественных отрицательных корня. Если система статически устойчива, то характеристическое уравнение (16), очевидно, позволяет определить частоты малых колебаний рассматриваемой механической системы в плоском случае.

Анализ корней кубического уравнения не представляет трудностей. Так, например, область статической устойчивости механической системы может быть изображена с помощью диаграммы Вышнеградского /4/. Для этого характеристическое уравнение (16) следует записать в форме Вышнеградского в3 + Арв2 + Врв +1 = 0, (17)

теряет устойчивость; 2) при выполнении условия A R x <  0 потеря статической устойчивости в системе возможна при переходе через ноль параметра A R x — A R у , что приводит к обнулению двух корней характеристического уравнения (16). Поэтому условие

A R x —A R y < 0 (19) также является необходимым условием статической устойчивости рассматриваемой механической системы.

Отметим в связи с этим, что значения параметров A R_x , A R у определяются массами каждого тела, а также соответственно их силами лобового сопротивления ( A R_x ) и их подъемными силами ( A R у ), и не зависят от длины троса.

где

в = з —X2

λ

новая переменная,

q _λ              r _λ

A в , /---Г   B e  , П—

³ t λ p λ ^{2 ,          3} t λ ² p λ

параметры

Вышнеградского.

Область статической устойчивости механической системы соответствует вещественным отрицательным корням кубического уравнения (17), что приводит к ограниченным гармоническим колебаниям в системе (14), и определяется неравенством

Выбор параметров аэродинамического стабилизатора и длины троса

Неравенство (18) удобно использовать при решении задач анализа статической устойчивости механической системы. Так, например, задаваясь параметрами связки СА и АС, можно вычислить значения величин

I Be f (Ав, Be)     3

—

A e i

9 J

+

A _β

• В в — 3

—

³ A _β

< 0 ,(18)

Анализируя решения алгебраического уравнения (16) в общем случае для тел с осевой симметрией и вид его коэффициентов, можно сделать следующие выводы: 1) необходимым условием статистической устойчивости движения механической системы для симметричных тел остается условие A R x <  0 , так как при A R x = 0 все корни уравнения (16) нулевые и при переходе параметра A R x через нулевое значение система

^Aβ , ^Bβ и определить статическую устойчивость системы. При решении задач синтеза, при решении проектных задач удобнее использовать другие методы, такие, например, как метод корневого годографа /5/. При анализе статической устойчивости движения системы классическим методом корневого годографа характеристическое уравнение (16) необходимо представить в виде

1 v P X) П

^{1 +} K • q X ) = °, (20) где P ( я ²) и Q ( я ²) - многочлены относительно λ ² , K – подбираемый параметр.

С учетом вида коэффициентов уравнения (16) при степенях λ , выбрать в качестве линейно входящего в уравнения параметра K возможно только длину троса r ₃ . В остальных

случаях использовать для построения корневых годографов стандартные средства математических пакетов не представляется возможным. Но, тем не менее, разрешимость корней кубического уравнения в аналитическом виде делает возможным построение корневого годографа для рассматриваемой системы и по любым другим параметрам системы.

Корневой годограф представляют собой совокупность траекторий корней характеристического уравнения (16) на комплексной плоскости. Построение корневого годографа по длине троса показало, изменение длины троса не может привести к потери статической устойчивости системы, если параметры связки удовлетворяют условиям (19) и (20).

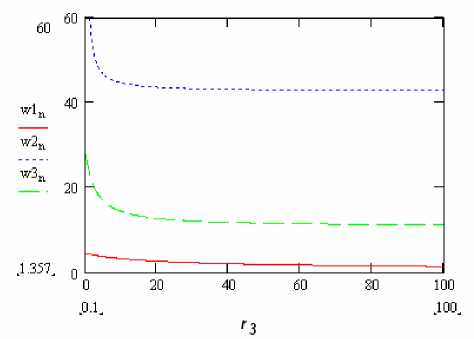
Рис. 2. Поведение частот системы при изменении длины троса

Изменяя длину троса можно лишь скорректировать частоты в системе. На рис. 2 показаны типичные зависимости частот системы от длины троса. Из этого рисунка можно сделать вывод, что увеличение длины троса приводит к уменьшению частот системы.

При проведении расчетов были приняты следующие исходные данные: т 1 = 10 кг , m 2 = 1 кг , 1 1 = 5 кг • м ², 1 ₂ = 0,4 кг • м ², С х 1 =- 1, С у 1 = 5, С х 2 =— 1, С у 2 = 1,2, S 1 = 2 м ², S ₂ = 1 м ², q = 1000 кг / м ², r 1 = 0,8 м , r ₂ = 1 м .

При выборе массы АС классический вариант метода корневого годографа не может быть применен, так как масса m ₂ стабилизатора входит в характеристическое уравнение системы нелинейно, что следует из уравнения (16). В этом случае корневой годограф был построен при длине троса, равной 10 метрам, с помощью прямого решения кубического уравнения (16) и приводится на рис.3. На рис.4 показаны значения левой части неравенства (18), позволяющие определить область статической устойчивости исследуемой системы в зависимости от массы АС. Как видно из рис. 4, система статически устойчива при массе АС, меньшей 4,8 кг.

,858.001} 000

Imiroot-l^l

Imlroot_2_n| q

Imlroot_3Il|

• -    858.00Ц qqq

  -110⁵     -8 IO⁴ -6 IO⁴ -410⁴     -2 IO⁴ 0

• -    9 974x 10⁴ Re (™t J J , Re (mo^J , Re (root_3_nj          10

Рис. 3. Вид корневого годографа для характеристического уравнения (19) при изменении массы АС

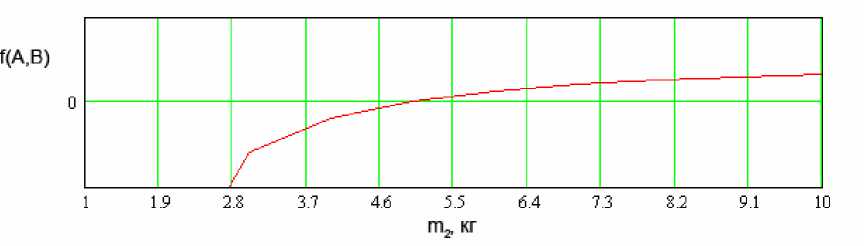
Рис. 4. Изменение функции f(A,B) при изменении массы АС