Двойные пучки Лагерра-Гаусса

Среди множества известных лазерных пучков самыми популярными и наиболее изученными являются пучки Лагерра–Гаусса (ЛГ) [1 –3]. Эти пучки сначала рассматривались как моды внутри резонаторов. В работе [4] пучки ЛГ получены вне резонатора с помощью астигматического конвертора из пучков Эрмита–Гаусса (ЭГ). Особенный интерес к пучкам ЛГ возник после работы Л. Аллeна и др. [5], в которой было установлено, что пучки ЛГ обладают орбитальным угловым моментом (ОУМ). Известны обобщения пучков ЛГ в виде пучков Эрмита–Лагерра–Гаусса [6, 7]. Известны элегантные [8] и эллиптические [9] пучки ЛГ. Интерес к пучкам ЛГ не ослабевает и в наши дни из-за их широкого применения в телекоммуникациях, манипулировании частицами, зондировании турбулентной атмосферы, квантовой информатике, охлаждении атомов. Например, в [10] проведено сравнение пучков ЛГ и пучков Бесселя–Гаусса (БГ). В [11 – 13] рассмотрены различные варианты генерации мод ЛГ на основе специального лазера, использующего усиленную внутрирезонаторную сферическую аберрацию [11], q-пластинки [12] или специальной метаповерхности [13]. В [14] обсуждается взаимное преобразование между модами ЭГ и модами ЛГ. Важное значение имеют исследования элегантных пучков ЛГ, демонстрирующих исключительные характеристики во многих областях, таких как оптическая связь и оптический захват [15]. Например, в работе [16] авторы предложили метод измерения топологического заряда частично когерентного элегантного пучка ЛГ. На основе пучков ЛГ разрабатываются новые типы оптических пучков, обладающих различными полезными свойствами. В [17] рассмотрено семейство асимметричных лазерных пучков ЛГ. В [18] предложен метод генерации таких пучков высокой мощности. Пучки ЛГ были использованы для генерации векторного пучка с пространственно-зависимой поляризацией в поперечном сечении посредством нелинейного магнитооптического вращения [19]. Новый класс составных вихревых пучков, получаемый путем коаксиального наложения пучков ЛГ с общим положением и параметром перетяжки, был представлен в [20]. В [21] был теоретически и экспериментально исследован новый тип частично когерентного пучка с необычной корреляционной функцией, названной эллиптической коррелированной моделью Лагерра–Гаусса–Шелла. Распределение интенсивности таких пучков в дальнем поле имеет эллиптический кольцеобразный профиль. Пучки ЛГ имеют высокую практическую значимость для оптических коммуникаций [22–25], микроманипулирования [26] и фотовозбуждения атомов [27].

В данной работе рассмотрен новый тип лазерного пучка – произведение двух пучков ЛГ или двойные пучки ЛГ. Комплексную амплитуду таких пучков можно разложить в конечную сумму обычных пучков ЛГ. Получено выражение для преобразования Френеля таких пучков. Рассмотрены некоторые частные случаи произведения двух пучков ЛГ, для которых найден явный вид Фурье-преобразования.

1. Теоретическое основание

Рассмотрим обычный ЛГ-пучок, комплексная амплитуда которого в начальной плоскости ( z =0) имеет вид [1]:

m

। r ² ii re~ i ^ф ।       ।   2 r

LG p ,± m ( r , ф ) = exp I-- т II-----I L ^mp I —

V w ² ) V w ) V w²

Из (3) следует, что произведение двух пучков ЛГ имеет топологический заряд (ТЗ), равный сумме ТЗ каждого из пучков ЛГ. Нормированный на мощность орбитальный угловой момент пучка (3) также равен сумме ТЗ каждого пучка ЛГ, то есть равен m + n .

Найдём теперь преобразование Френеля от функции (3), воспользовавшись разложением произведения двух многочленов Лагерра в конечную сумму многочленов Лагерра с удвоенным аргументом:

p ⁺ q

L mp ( x ) L nq ( x ) - ^ C k L m ⁺ n (2 x ), (5) k -0

где C k - 2 q - ^k P p ⁽++ ^m ,T q • ^{k + n} - ^p ) (0) P q^k - ^q • ^p - ^k ) (0) и P n ⁽^- ^V ’ ( - ) -многочлены Якоби [28]. Используя (5), можно представить амплитуду дЛГ-пучков (3) в виде конечной суммы обычных пучков ЛГ:

где ( r , ф) - полярные координаты, p , ± m - радиальный и азимутальный индексы, w – радиус перетяжки Гауссова пучка, L ^mp ( x ) – многочлен Лагерра. Так как пучок (1) является модовым пучком, то есть при распространении в свободном пространстве сохраняет структуру интенсивности, то комплексная амплитуда пучка ЛГ на любой плоскости z описывается выражением, подобным (1):

/ x /      x m + n

„ z z i     r ² ii re ^ф 1

dLG p , q , m , n ( r , ф ) - exp |--- ||-----| X

I w ² )l w )

p+q         ( 7f2     p+q x^ CkLm+n I т I - X CkLGk,m+n (r, ф).

k -0          V ^w ) k -0

Выражение (6) позволяет легко найти амплитуду поля (3) на любом расстоянии z :

A exP ⁽ " i ⁽² P ⁺ m ^{+ 1)a} rg ^{O )}

LG p , ± m ( r , ф , z ) =-----------n-----------

°l

p+q dLG p,q,m,n (r, ф, z) - X CkLGk,m+n (r, ф, z).           (7)

k -0

X exp

Г ■ 2 ) izr ²

_V z 0 W ² |o|² ₎

LG

r

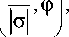
где О =1+ iz / z о - вспомогательный комплексный параметр, z ₀= л w ²/ X - длина Рэлея и X - длина волны. Тем самым, w | о |=[1+( z / z ₀)²]^1/2 - радиус Гауссова пучка, (2 p +m +1) arg О = (2 p +m +1) arctg ( z / z ₀) - фаза Гоу.

Далее мы будем исследовать только ЛГ-пучки с неотрицательными азимутальными индексами.

Рассмотрим произведение двух пучков вида (1), которое будем называть двойным ЛГ (дЛГ)-пучком:

dLG p , q , m , n ( r , ф ) =

Из (7) видно, что дЛГ-пучки (3) при распространении в свободном пространстве не сохраняют свою структуру, поскольку в суперпозиции (7) присутствуют пучки ЛГ с разной фазой Гоу. Но так как распределение интенсивности в сечении пучка (7) имеет вид набора соосных колец, максимальное число которых равно p + q + 1, то изменение картины дифракции при распространении пучка (7) сводится к перераспределению световой энергии между кольцами.

Рассмотрим далее частный случай дЛГ-пучков, когда оба многочлена Лагерра одинаковы. Мы назвали его пучком «ЛГ в квадрате», (ЛГ)2. Такой пучок в начальной плоскости вместо (3) имеет амплитуду

- (V2) ^{m +} n LG p , m I -y=,ф) LG q , n I -^2,ф) -

dLG p , p , m , m ( r , ф ) - 2 m

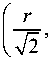
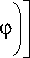
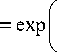
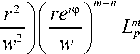
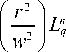
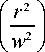
^L G p , m

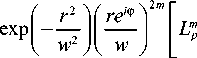
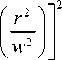
Мы добавили масштабные множители 2 , чтобы в итоге оставить неизменной Гауссову составляющую.

Семейство пучков (3) зависит от четырёх целочисленных индексов и является в некотором смысле обобщением обычных пучков ЛГ (1), так как при p = q =0 совпадает с однокольцевыми пучками ЛГ:

/    -> N /     N m + n

I r2 II reф I dLG0,0, m, n (r, ф) - exp |--- ||----|    - LG0, m+n (r, ф)- (4)

V w ² )( w )

Отметим, что в отличие от общего случая разложение (7) пучка (ЛГ)2 состоит только из чётных членов (нечётные обнуляются), а сами коэффициенты, благодаря формуле (4.4.1.9) из [28], имеют более простой вид:

p dLGp,p,m,m (r, ф) - X C2kLG2k,2m (r, ф), k-0

C 2 k - C 2 k ( p , p , m , m ) -

( p + m )!(2 k )!(2 p - 2 k )!

2 ^{2 p} p ! k !( m + k )!( p - k )! ^{2 -}

Пучок (8) так же, как и общий пучок (3), не модовый и не сохраняет структуру интенсивности. Но в отличие от (3) пучок (8) сохраняет свою структуру в дальней зоне, то есть является Фурье-инвариантным. Это следует из разложения (9), так как хорошо известно, что любая суперпозиция ЛГ-пучков является Фурье-инвариантной, если азимутальные индексы всех пучков в суперпозиции одинаковы, а радиальные индексы или все чётны, или все нечётны. Чтобы получить явные аналитические выражения, определим сначала интегральное преобразование, обобщающее преобразования Френеля и Фурье:

при условии неотрицательности азимутальных индексов, q + n – p и p + m – q . Как простое следствие, любой дЛГ-пучок является Фурье-инвариантным, если p + m = q + n .

Из (6) легко получить выражение для «энергии» двойного пучка ЛГ, которое можно использовать для нормировки таких пучков:

^ 2л

W - J J |dLG p , q , m , n ( r , ф )|² rdrd ф-

FR z,f [ F ( p )]( r ) -

p + q         ^{1X1 2 л}

- S l ^C^ |² J J |LG k , m + n ( r , ф )|² rdrd ф- k ^{- 0}        0 0

[[exp ^f iZ 0 . Ы n z &  z

w ²

- iz -ИЕ-] F (p) d "

J w ² I       w²

При f = x и z = f получаем соответственно преобразование Френеля и преобразование Фурье с дополнительным дефокусировочным множителем. Здесь r = ( r cos ф , r sin ф ) и p = ( p cos 0 , p sin 0 ) - двумерные векторы. Для краткости будем, как и ранее, записы-

вать аргументы, просто указывая полярные координаты: F( p )=F( p , 0 ).

Нетрудно показать, что

FR z , f [LG p ,± m ( p , 0 )]( r , ф ) -

e - i (2 p + m +1)arg a

I 5

X

x exp

" ir ²

A

. ^{w 2} l^a 12

z z0

^z o + ^z o ^z ff ²

LG p ,± m

r

VA ^, Ф

« J

где a - a - z/f - 1 - z/f + iz/z 0 . В частности, если f = x , то (11) сводится к (2).

Если z = f , то a - if/z o и arg a -л/ 2. Поэтому (11) после сокращения на exp ( iz ₀ r ²/ f w 2 ) сводится к хорошо известной Фурье-инвариантности ЛГ-пучка:

x 2л

J J exp

л w ²

) m + n +1

p ^ q с 2 ( k + m + n )!

^Sl k¹ k !

.

2. Численное моделирование

На рис. 1 показаны распределения интенсивности и фазы стандартных пучков Лагерра–Гаусса (1) двух разных порядков и двойного пучка Лагерра–Гаусса (3) с этими же порядками в начальной плоскости и на расстоянии Рэлея. Распределения в начальной плоскости получены с помощью формул (1) и (3), а на расстоянии Рэлея – с помощью преобразования Френеля.

2 iz о              )             p d p d 0

-—у rp cos(ф-0) I LGp,±m (p, 0)       - fw2           J            w

-л ( - i ) ^{2 p + m} LG p ,± m f f , ф

Рис. 1. Распределения интенсивности (столбцы 1 и 3) и фазы (столбцы 2 и 4, тёмный цвет – 0, белый цвет – 2π) стандартных пучков Лагерра–Гаусса (1) порядков (m, p) = (1, 2) (ряд 1) и (n, q) = (4, 3) (ряд 2), а также двойного пучка Лагерра–Гаусса (3) порядка (m, p, n, q) = (1, 2, 4, 3) (ряд 3) в начальной плоскости z = 0 (столбцы 1 и 2) и на расстоянии Рэлея z = z 0 (столбцы 3 и 4) при следующих параметрах: длина волны λ = 532 нм, радиус перетяжки w = 0,5 мм. Масштабная метка на всех рисунках означает 1 мм. Пунктирная окружность на распределениях фазы – контур, по которому рассчитывался топологический заряд. Кривые на распределениях в нижнем ряду (и, л)

Применяя это равенство к дЛГ-пучку (9), получаем

^{2л    f} 2iz o         _QJ,_T„ / _mp d p d 0

exp I -TT r p cos( ф- 0 ) I dLG p , p , m , m ( p , 0 )        -

0 0 I ^fw 2             J                  w ²

-Л ( - 1) m dLG p , p , m , m f z ⁰ ^ , ф|

Можно показать, что Фурье-образ любого дЛГ-пучка (3) также является дЛГ-пучком:

показывают сечения интенсивности

H ^f 2 iz o            )             p d p d 0

exp I -    rp cos(ф- 0) I dLGp,q,m,n (p, 0)

fw2

- n ( - i ) ² p ⁺ m ^{+ 2} q ⁺ n dLG p , q , q + n - p , p + m - q ^f     , ф

Из рис. 1 видно, что распределения интенсивности сохраняются при распространении обоих стандартных пучков ЛГ, но у двойного пучка ЛГ распределение интенсивности меняется. В частности, в начальной плоскости самым ярким является первое кольцо (наименьшего радиуса), а на расстоянии Рэлея – вто-

рое. Согласно формуле (3), у пучка должно быть p + q + 1 =6 колец интенсивности. Однако на рис. 1 и видно только четыре, а на рис. 1 л – пять. Тем не менее сечение интенсивности на рис. 1 и и распределение фазы рис. 1 к подтверждают соответственно наличие шести световых колец и пяти теневых колец между ними (где фаза меняется на π). На рис. 1 л два кольца объединяются и их остаётся пять.

Как и предсказывает формула (3), ТЗ пучка (3) равен сумме ТЗ пучков (1) (1 +4=5). Это видно из распределений фазы: на рис. 1 в , г ТЗ равен 1 (один скачок фазы на 2π вдоль пунктирной окружности), на рис. 1 е , з ТЗ равен 4 (четыре скачка фазы вдоль окружности), а на рис. 1 к , м ТЗ равен 5 (пять скачков фазы вдоль окружности).

Заключение

В данной работе рассмотрено 4-индексное семейство вихревых пучков, пересекающееся с семейством хорошо известных пучков ЛГ. Эти пучки представляют собой произведение двух разных пучков ЛГ с одинаковым радиусом перетяжки (сокращенно дЛГ-пучки). Если у дЛГ-пучка оба многочлена Лагерра имеют одинаковые индексы, то такой пучок можно назвать пучком Лагерра–Гаусса в квадрате, (ЛГ)2. Получено разложение дЛГ-пучка в конечную сумму обычных пучков ЛГ. Получен явный вид Фурье-преобразования для пучка (ЛГ)2. Двойные ЛГ-пучки могут найти применение в оптических коммуникациях [22, 24].

Работа выполнена при поддержке Российского научного фонда (грант № 22-12-00137).