Двуцветный граф как средство классификации декартовых произведений грубых преобразований окружности

В 1959 году М. Пейшото в статье [3] обобщил результаты А. А. Андронова и Л. С. Понтрягина на произвольные ориентируемые замкнутые поверхности. В дальнейшем гиперболическая теория начала активно развиваться, С. Смейлом, Дж. Палисом, В. ди Мелу [4–6] была выстроена теория простейших структурно устойчивых систем, неблуждающее множество которых состоит из конечного числа орбит, называемых системами Морса-Смейла (в книге [7] дано систематизированное изложение классификации систем Морса-Смейла).

В 1971 году М. М. Пейшото в работе [8] формализовал понятие схемы Леонтович-

Майера (введенное в 1955 г. в работе [9]) и доказал, что для систем Морса-Смейла на произвольных поверхностях, полным топологическим инвариантом является класс изоморфности его различающего графа. Результат Пейшото был обобщен В. З. Гринесом и А. Н. Безденежных для градиентно-подобных каскадов на ориентируемых поверхностях [10]. В работе [11] А. А. Ошемков и В. В. Шарко предложили поставить в соответствие потоку Морса-Смейла без замкнутых траекторий на поверхности трехцветный граф, который также является полным топологическим инвариантом, но по сравнению с графом Пейкшото, описание и проверка изоморфности трехцветных графов является значительно более простой. В работе [12] были классифицированы градиентно-подобные диффеоморфизмы на поверхностях посредством трехцветного граф ( T f , Pf ). В статье [13] получена полная топологическая классификация n -кратных регулярных гомеоморфизмов окружности.

В настоящей работе рассматривается более узкий, по сравнению с работами [12; 13], класс G* диффеоморфизмов, представляющих собой декартово произведение двух грубых преобразований окружности. В качестве претендента на роль топологического инварианта систем класса G* предъявляется двуцветный граф и доказывается теорема о полноте множества найденных инвариантов.

Теорема. Диффеоморфизмы f, f G G* топологически сопряжены тогда и только тогда, когда двуцветные графы ( D f , P f ) и ( D f’ , P f-’ ) изоморфны.

Пусть f:М²^М² - диффеоморфизм класса G * , представляющий собой декартово произведение двух грубых преобразований окружности.

Неблуждающее множество П диффеоморфизма f: М² ^ М² представляется в следующем виде объединения множества стоковых (П₀), седловых (П 1 ) и источниковых (П₂) точек диффеоморфизма f, то есть: ^ = 0 0 9^ 1 0^ 2 . Множество П 1 ^0 в силу того, что диффеоморфизмы класса G* являются декартовым произведением двух грубых преобразований окружности и имеют по крайней мере две седловые точки, фазовый портрет простейшего представителя класса G* представлен на Рис. 3.

Следующее утверждение устанавливает топологический тип многообразий, допускающих диффеоморфизмы из класса G *.

Утверждение. Пусть f G G*. Тогда М² гомеоморфно либо тору Т², либо бутылке Клейна ^².

Двуцветный граф.

Определение. Граф D называется двуцветным графом , если:

• 1)    множество всех ребер графа D является объединением двух подмножеств, каждое из которых состоит из ребер одного цвета (цвета ребер обозначим буквами s , и );

• 2)    каждая вершина графа D инцидентна в точности четырем ребрам, причем из них два 2

ребра цвета и , два ребра цвета s ;

• 3)    граф не содержит петель.

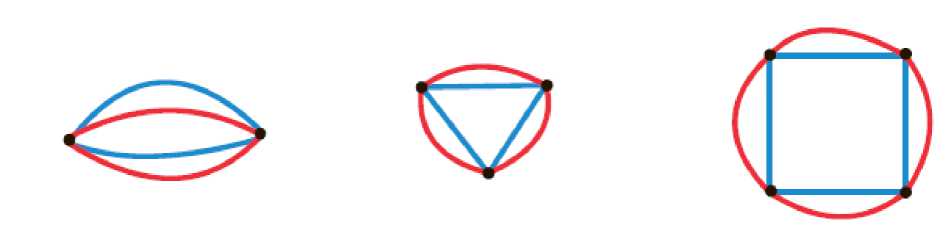
Рис. 1. Примеры двуцветных графов с двумя, тремя и четырьмя вершинами.

На рисунке 1 приведены примеры простейших двуцветных графов; в силу определения двуцветного графа (он не содержит петель) минимально возможный двуцветный граф состоит из 2 вершин и 4 соединяющих их ребер.

Взаимно-однозначное отображение P графа D на себя, переводящее вершины в вершины с сохранением отношений инцидентности и цветности, называется автоморфизмом графа D . В дальнейшем мы будем понимать под символом ( D, P ) граф D , оснащенный автоморфизмом P .

Два двуцветных графа (D, P) и (D', P') назовем изоморфными,   если существует взаимно-однозначное/ \

Г / \ Г соответствие % между множествами их вершин, сохраняющее         /\ отношения инцидентности и цветности, при этом сопрягающее       /\ автоморфизмы P и P' , то есть P' % = % P.                            \/

Опишем процесс построения двуцветного графа для диффеоморфизмов класса G *, для этого проведем предварительные разбиения поверхности.

Положим М = M²\(W^_o U W^ U М щ U W ^₂ ).             Рис. 2. Вид ячейки.

Множество М представляется в виде объединения областей (ячеек), гомеоморфных открытому двумерному диску, граница каждой из которых имеет вид, изображенный на Рис. 2.

В границу каждой ячейки 8 входят четыре периодические точки: источниковая точка а, седловые точки с и o j , стоковая точка щ, а также устойчивые сепаратрисы 1 ^. и l ^s_a. ( s -кривые) с граничными точками а, с и а, G j , неустойчивые сепаратрисы 1%. и 1 %. ( и -кривые) с граничными точками щ, с ^ и o j , щ (см. Рис. 2). Стороной ячейки назовем замыкание s - или и -кривой.

Периодом ячейки 8 называется наименьшее натуральное число к Е N, такое что f k (8) = 8.

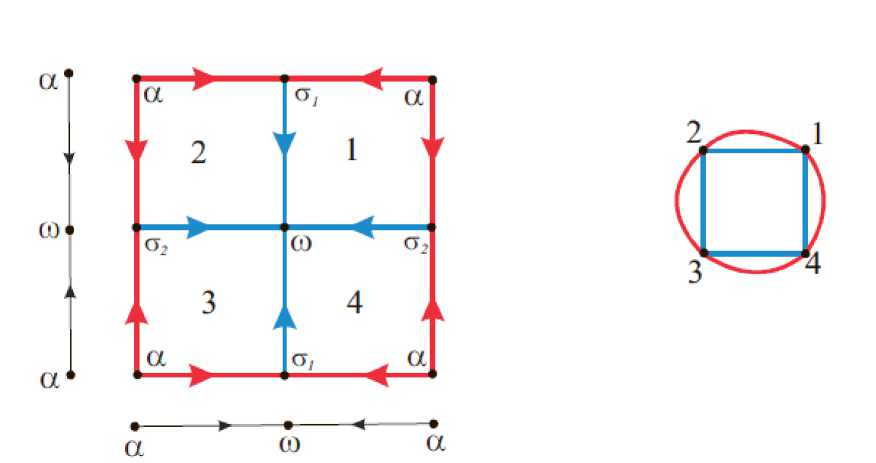
Рис. 3. Фазовый портрет диффеоморфизма класса

G* и соответствующий ему двуцветный граф.

Перейдем к непосредственному процессу построения двуцветного графа D f , соответствующего диффеоморфизму f G G* (см. Рис. 3-4).

• 1)    Вершины графа D f взаимно-однозначно соответствуют ячейкам множества △ ;

• 2)    две вершины графа инцидентны ребру цвета s или и , если соответствующие этим вершинам ячейки имеют общую s или u кривую.

Обозначим через B f множество вершин графа D f . Так как каждая ячейка имеет 4 стороны и из них две имеют цвет и , оставшиеся две - цвет s , то в вершине, соответствующей ячейке, сходятся 4 ребра, причем из них два ребра цвета u, два ребра цвета s.

Цикл, все ребра которого имеют цвет и ( s ) назовем и ( s )-циклом; su -циклом назовем цикл, цвета всех ребер которого чередуются. Так как две вершины графа могут быть инцидентны двум ребрам различного цвета, то для однозначности условимся, что при описании su -цикла первое ребро имеет цвет s .

Поскольку все стороны ячейки различны, то есть любая сторона ячейки примыкает к стороне другой ячейки, то граф D f не имеет петель.

Таким образом, граф D f удовлетворяет определению двуцветного графа. Положим ду взаимно-однозначное отображение множества ячеек диффеоморфизма f на множество вершин графа Df. Диффеоморфизм f индуцирует на множестве вершин и ребер графа D f автоморфизм P f = ^-fn -' .

Лемма. Двуцветный граф ( D f , P f ) обладает следующими свойствами:

• 1)    граф D f связен;

• 2)    каждое ребро принадлежит единственному su -циклу длины 4; каждый s-цикл имеет

длину 4; каждый u-цикл имеет длину 4.

• 3)    автоморфизм P f является периодическим с периодом mf.

Для диффеоморфизмов класса G *, представляющих собой декартово произведение двух грубых преобразований окружности, найдены необходимые и достаточные условия топологической сопряженности диффеоморфизмов посредством двуцветного графа, которые сформулированы в следующей теореме.

Теорема. Диффеоморфизмы f , f' из класса G * топологически сопряжены тогда и только тогда, когда графы ( D f ; P f ), ( D f' ; P f' ) изоморфны.

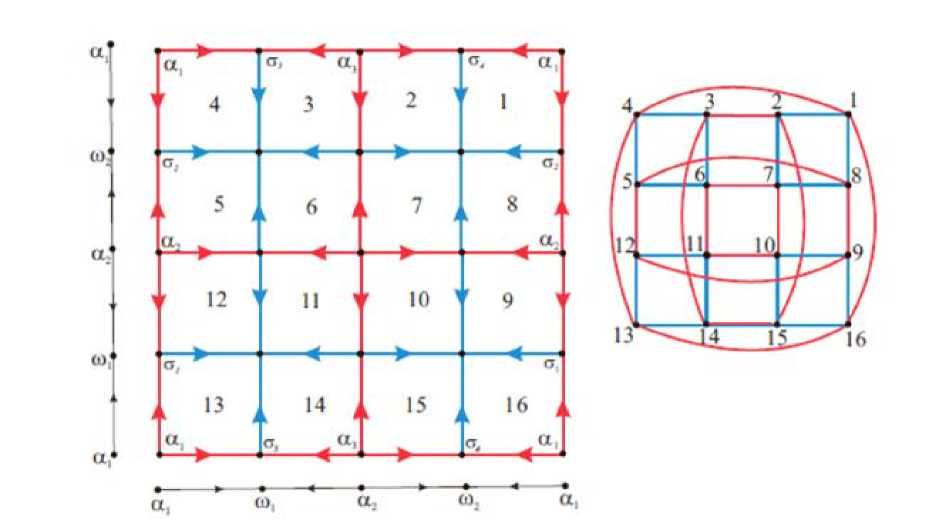
Рис. 4. Фазовый портрет диффеоморфизма класса G* и соответствующий ему двуцветный граф.

Заключение. В статье описан алгоритм сопоставления каждому диффеоморфизму, представляющему собой декартово произведение двух грубых преобразований окружности, двуцветного графа. Найдены необходимые и достаточные условия топологической сопряженности диффеоморфизмов, представляющих собой декартово произведение двух грубых преобразований окружности, посредством двуцветного графа.