Двух- и трехпараметрические модели связи высоты деревьев с диаметром на высоте 1,3 м в дубовых древостоях

Автор: Дубенок Н.Н., Кузьмичев В.В., Лебедев А.В.

Журнал: Лесохозяйственная информация @forestry-information

Статья в выпуске: 3, 2021 года.

Бесплатный доступ

К настоящему времени накоплено много данных о результатах обмеров высот и диаметров стволов деревьев на высоте 1,3 м. Использование аналитического метода при построении связей высот и диаметров стволов показало наличие закономерностей изменений характера кривых высот в зависимости от возраста, полноты и производительности древостоев. Это позволило разработать методы математического описания зависимости параметров кривых высот от морфолого-таксационных показателей конкретных древостоев. По материалам измерения модельных деревьев в дубовых древостоях была отобрана наиболее адекватная модель среди множества 2- и 3-параметрических, которая передает зависимость между высотой деревьев и диаметром стволов на высоте 1,3 м. В исследовании использованы данные обмеров деревьев на 6 постоянных пробных площадях с 1910 по 2010 г. Возраст древостоев на момент проведения измерений - от 10 до 130 лет. Комплексная оценка метрик качества 2- и 3-параметрических моделей выявила, что лучшей обобщающей способностью характеризуются 2-параметрические модели. В качестве лучшей модели обоснована логарифмическая зависимость высот деревьев дуба от диаметров стволов на высоте 1,3 м. Модель смешанных эффектов более точно прогнозирует значения высот по сравнению с моделью фиксированных эффектов. Недостающие значения высот большого количества деревьев на участке можно вычислить более точно с помощью модели смешанных эффектов, а не применяя модель фиксированных эффектов или используя только фиксированную часть (средний отклик) модели смешанных эффектов. Применение разработанной модели должно ограничиваться только теми условиями, к которым относятся экспериментальные материалы.

Еще

Высота ствола, диаметр дерева на высоте 1, 3 м, дуб, модель смешанных эффектов

Короткий адрес: https://sciup.org/143178047

IDR: 143178047 | DOI: 10.24419/LHI.2304-3083.2021.3.04

Текст научной статьи Двух- и трехпараметрические модели связи высоты деревьев с диаметром на высоте 1,3 м в дубовых древостоях

Объем отдельных деревьев и их совокупностей длительное время устанавливали с помощью таблиц объемов стволов. Для определения запаса древесины поступающих в рубку древостоев использовали данные сплошных перечетов деревьев по ступеням толщины и взаимосвязи высот и диаметров, получившие в лесной таксации название «графика высот». Для сочетаний высот и диаметров по ступеням толщины подбирали объемы стволов (из таблиц объемов деревьев), находили объемы деревьев в ступенях толщины и в результате их суммирования получали запас древесины. Следует отметить, что вследствие повышенной трудоемкости измерения высоты ее определяли для 15–25 деревьев [1, 2].

Увеличение объемов отпуска древесины привело к стандартизации связей высот и диаметров деревьев в таблицах объемов стволов, введению разрядов высот. Они представляют собой линии связи высот и диаметров в спелых древостоях данной породы в разных условиях произрастания определенного района. Обычно линии подбирали таким образом, чтобы разница в объеме стволов одинаковой толщины, но разных высот составляла 5 %. Для определения разряда высот таксируемого древостоя замеряли высоты у 5–6 деревьев в центральных ступенях толщины, что позволяло сократить трудозатраты.

Проведение хозяйственных мероприятий в более молодых древостоях (в частности, рубок ухода) также требовало определения запаса древостоев с использованием графиков высот. После накопления значительного объема данных таких обмеров и использования аналитического метода при построении связей высот и диаметров были выявлены некоторые закономерности изменений характера кривых высот в зависимости от возраста, полноты и продуктивности древостоев. На основе этого были разработаны методы математического описания зависимости параметров кривых высот от морфолого-таксационных показателей конкретных древостоев [3, 4].

Цель исследования – по материалам измерения модельных деревьев в дубовых древостоях среди множества 2- и 3-параметрических моделей связей выбрать наиболее адекватную, которая отражает зависимость между высотами деревьев и диаметрами ствола на высоте 1,3 м.

Материалы и методы исследования

Объектом исследования стали дубовые древостои на постоянных пробных площадях в Лесной опытной даче Российского государственного агарного университета – МСХА имени К.А. Тимирязева. Площадь территории Лесной опытной дачи составляет 248,6 га. В конце XVII – начале XVIII в. на ее территории, по свидетельству А.Р. Варгаса де Бедемара, произрастали дубовые насаждения с примесью липы, клена и незначительным присутствием сосны, березы и осины. М.К. Турский отмечал, что на момент межевания 1763 г. здесь преобладали насаждения лиственных пород с единичным участием хвойных. Площади с преобладанием дуба сократились с 30 га в 1862 г. до 12 га в 1915 г. Позже они стали увеличиваться в результате разрушения сосняков естественного происхождения и освобождения дуба из второго яруса. В 2009 г. они занимали уже 60 га. Общий запас древесины с 1962 по 2009 г. возрос с 9,5 тыс. до 15 тыс. м ³ , в основном за счет естественных процессов роста. Средний запас древесины в 2009 г. составил 250 м ³ /га [5–7].

В исследовании использованы данные обмеров деревьев на 6 постоянных пробных площадях с 1910 по 2010 г. Возраст древостоев варьировал от 10 до 130 лет. По итогам 23 перечетов измерены высоты и диаметры у 418 деревьев. Диаметр стволов растущих деревьев на высоте 1,3 м измеряли мерной вилкой, а высоты – с помощью механического высотомера. Для анализа случайным образом отобраны данные, которые были разделены на обучающую и тестовую выборки в соотношении 7 : 3. Обучающую выборку использовали для подгонки модели, а тестовую – для проверки обобщающей способности.

Таблица 1. Описательная статистика экспериментальных данных

Показатель	Обучающая выборка				Тестовая выборка
Показатель	Mean	Min	Max	SD	Mean	Min	Max	SD
DBH, см	25,34	4,20	56,90	7,68	24,95	9,50	42,00	6,97
h, м	19,09	6,76	28,00	3,50	19,15	10,31	27,70	3,20
Dq, см	24,29	4,60	33,10	4,49	24,38	4,60	33,10	4,22
H, м	18,79	8,50	25,60	3,03	18,84	8,50	25,60	2,90

Примечание: Mean – средняя арифметическая; Min – минимальное значение; Max – максимальное значение; SD – среднеквадратическое отклонение; DBH– диаметр на высоте 1,3 м; h – высота дерева, м; Dq – среднеквадратический диаметр древостоя, H – средняя высота древостоя.

Таблица 2. У равнения связи высот с диаметрами

№ модели	Уравнение			Литературный источник
2-параметрические модели
M1	h = 1,3 + b 1 DBH^b ²			J. Huxley и G. Teissier [8]
M2	h = 1,3 + \| (	DBH b 1 + b 2 DBH	² )	M. Naslund [9]
M3	h =1,3+ bDBBHL b 2 + DBH			S. Huang с соавт. [10]
M4	h = 1,3 + b 1	< DBH t1+ DBH J	b ₂	S. Huang с соавт. [10]
M5	h = 1,3 + b 1	fl + ' ( DBH J	b ₂	R.O. Curtis [11]
M6	b ₁ DBH h — 1,3 + l (1 + DBH ) b ²			R.O. Curtis [11]
M7	h = 1,3 + b 1 (1 - exp( - b 2 DBH ))			H.A. Meyer [12]
M8	h = 1,3 + exp	(. b₂ ) b +-- ²— ( ¹ DBH +1J		W.R. Wykoff с соавт. [13]

Окончание табл. 2

№ модели	Уравнение		Литературный источник
M9	h =1,3+____ ^bbDBH____ ( DBH +1) + b 2 DBH				D.M. Bates и D.G. Watts [14]
M10	h = 1,3 + b 1 DBH exp(- b 2 DBH )				S. Huang с соавт. [10]
M11	h = 1,3 + ex	(. b p b. + —- ( ¹ DBh		}	C. Staudhammerи V. Le May [15]
M12	h = 1,3 + b 1 exp^		b 2 DBH	)	M.A. Buford [16]
M13	h = 1,3 + 6 1 (10(1 + DBH )) b ²				H.O. El Momoun с соавт.[17]
M14	h = 1,3 + ^	bi ) b + —— ¹ DBH )		5	H.O. El Momoun с соавт. [17]
M15	h = 1,3 + Г	r Jl ( DBH	) b 2 ] "	1	F.N. Ogana [18]
3-параметрические модели
M16	h = 1,3 +---- b - 1 + b 2 DBH ^- ^b ³				S. Huang с соавт. [10]
M17	DBH ² h —1,3 + _ b 1 + b 2 DBH + b ₃ DBH ²				S. Huang с соавт.[19]
M18	h = 1,3 +------- b-------- 1 + b 2 exp( - b ₃ DBH )				S. Huang с соавт.[19]
M19	h = 1,3 + 6 , (1 - exp( - b 2 DBH b ))				R.C. Yangс соавт.[20]
M20	h = 1,3 + b 1 (1 - exp( - b 2 DBH )) ^b ³				C. Peng с соавт.[21]
M21	h = 1,3 + b 1 exp(- b 2 exp(- b ₃ DBH ))				S. Huang с соавт.[19]
M22	h = 1,3 + exp( b 1 + b 2 DBH b )				D.R. Larsen и D.W. Hann [22]
M23	h = 1,3 + exp	b ) b + —²— _ч ¹ DBH + b ₃ J			D.A. Ratkowsky [23]
M24	h = 1,3 + b 1 exp(- b 2 DBH ^b ³ )				A.R. Stage [24]
M25	1 h = f1,3 b + ( b b -1,3 b ) 1 - ^exp( - ^b ³ DBH ) ) b ( 1 - exp(-100 b ₃ ) J				J. Schnute [25]
M26	h = 1,3 + b 1 4DBh + b 2 DBH + b ₃ DBH ²				О.А. Атрощенко [26]
M27	h = 1,3 +------- b ¹ „ _r 1 + ( b 2 DBH^b ³ )^- ¹				W. Peschel[27]
M28	h = 1,3 + b 1 DBH^b ² ^DBH ~ b ³				E. Sibbesen [28]
M29	b ₁ h = 1,3 + DBH^b ² ⁺ ^b ³ DBH				H.O. El Momoun с соавт. [17]

Примечание: h – высота дерева, м; DBH – диаметр ствола дерева на высоте 1,3 м; b – параметры модели.

Описательная статистика экспериментальных данных приведена в табл. 1.

На первом этапе методика анализа данных предполагала построение парных визуализаций зависимости высоты от диаметра и проверку выборок на наличие выбросов. В дальнейшем проводили определение параметров для 15 двухпараметрических (M1-M15) и 14 трехпараметрических простых моделей (M16-M29), наиболее часто встречающихся в литературных источниках (табл. 2).

Сравнение оценок для каждой из моделей основывалось на численном и графическом анализе остатков. Для каждого полученного уравнения рассчитывали следующие метрики, позволяющие определить качество модели:

V квадратный корень из среднеквадратической ошибки (RMSE):

RMSE =

■у ( yi ^- yi )

^ n ’

V средний процент абсолютной ошибки (MAPE):

MAPE = 100 x ^	yt - yi	/ n
	y_i

V коэффициент детерминации (R 2 ):

_Р2 . К у - У) ) ² R = 1 — ,

К у ^- У ) ⁾ ²

V скорректированный коэффициент детерминации (R ² _adj.):

R^ = 1 - (1 - R ²)(^-, ( n - к )

V информационный критерий Акаике (AIC):

~ 2?

AIC = 2 k + n ln ^ y¹ y ¹ , n

V информационный критерий Байеса (BIC):

У ( у, - У) ) ²

BIC = k ln n + n ln—--------,

n где:

k – количество параметров модели;

n – количество наблюдений;

y_i – фактическое значение;

^{^} y_i – прогнозируемое значение по модели;

y – среднее фактическое значение.

Модель, для которой получены наибольшие значения коэффициентов детерминации и наименьшие значения информационных критериев, среднеквадратической ошибки и среднего процента абсолютной ошибки, признавалась лучшей.

Для моделей проводили графический анализ полученных кривых, так как их формы могут значительно отличаться, даже если статистика качества моделей аналогична [29].

На заключительном этапе уравнению, обоснованному в качестве лучшего, давали оценку с использованием регрессионной модели смешанных эффектов для устранения случайного влияния отдельных групп наблюдений на фиксированные параметры. Регрессионные модели смешанных эффектов находят широкое применение при изучении связи между высотами и диаметрами деревьев [30]. Анализ данных проводили с использованием R – языка программирования для статистической обработки и Python – мультипарадигмального языка программирования. Указаны версия используемого языка и пакеты с версией для обработки данных: Python 3.5 + NumPy 1.17.1 + SciPy 1.3.2 и R 3.6.3 + lme4 1.1.

Результатыи обсуждение

Итоговая сводка по пяти лучшим 2- и 3-па-раметрическим моделям приведена в табл. 3. На обучающей выборке лучшее качество из всех по комплексу метрик показывает 3-параметриче-ская модель M18. Но при оценке обобщающей способности на тестовой выборке лучше оказались 2-параметрические модели. По комплексу метрик качества на обучающей и тестовой выборках в качестве лучшей признана 2-параме-трическая модель M13.

Оценки параметров для 5 лучших двух-и трехпараметрических моделей представлены в табл. 4. Для всех рассмотренных 2-параметри-ческих моделей оцененные параметры являются статистически значимыми при p-значении < 0,05. Среди 3-параметрических моделей статистически незначимые оценки параметров выявлены для модели М17: для параметра b ₁получено p-значение 0,135.

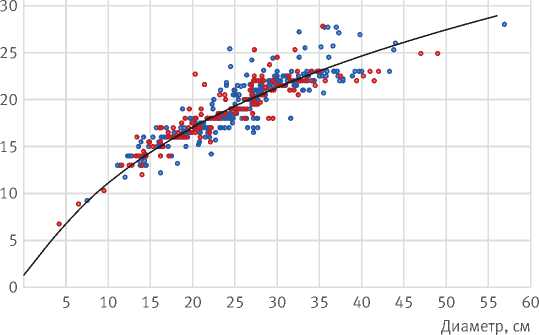
Графическая визуализация для модели M13, обоснованной в качестве лучшей, представлена на рис. 1. Кривая зависимости высот от диаметров исходит из точки 1,3 м, имеет горизонтальную асимптоту, поэтому удовлетворяет требованиям, предъявляемым к таким функциям [31, 32]. При сопоставлении фактических и прогнозируемых высот основная часть точек

Таблица 3. Итоговая сводка по пяти лучшим 2- и 3-параметрическим моделям

№ модели	Обучающая выборка						Тестовая выборка
№ модели	RMSE	MAPE	R²	R²-adj.	AIC	BIC	RMSE	MAPE	R²	R²-adj.	AIC	BIC
2-параметрические модели
M1	1,470	5,510	0,805	0,803	229,1	236,4	1,534	5,515	0,816	0,813	111,8	117,4
M3	1,465	5,561	0,806	0,805	226,9	234,2	1,485	5,491	0,827	0,824	103,6	109,3
M6	1,469	5,510	0,805	0,804	228,6	235,9	1,527	5,452	0,817	0,814	110,7	116,3
M10	1,476	5,682	0,803	0,802	231,3	238,7	1,487	5,729	0,827	0,824	104,0	109,7
M13	1,464	5,528	0,806	0,805	226,8	234,1	1,496	5,436	0,825	0,822	105,5	111,2
3-параметрические модели
M17	1,459	5,498	0,807	0,805	226,8	237,8	1,504	5,520	0,823	0,818	108,9	117,4
M18	1,448	5,447	0,810	0,808	222,3	233,3	1,507	5,726	0,822	0,818	109,3	117,8
M19	1,461	5,507	0,807	0,805	227,3	238,4	1,490	5,346	0,826	0,822	106,5	115,0
M20	1,460	5,504	0,807	0,805	227,1	238,1	1,490	5,330	0,826	0,822	106,4	114,9
M23	1,458	5,492	0,808	0,806	226,3	237,3	1,499	5,455	0,824	0,819	108,0	116,5

Таблица 4. Оценки параметров 5 лучших 2- и 3-параметрических моделей

№ модели	Параметр	Оценка	t-статистика	p-value
2-параметрические модели
M1	b ₁	2,725e+00	1,731e+01	< 2e-16
M1	b ₂	5,848e-01	3,339e+01	< 2e-16
M3	b ₁	4,425e+01	2,320e+01	< 2e-16
M3	b ₂	3,627e+01	1,339e+01	< 2e-16
M6	b ₁	2,931e+00	1,643e+01	< 2e-16
M6	b ₂	4,324e-01	2,371e+01	< 2e-16
M10	b ₁	1,066e+00	5,158e+01	< 2e-16
M10	b ₂	1,538e-02	2,271e+01	< 2e-16
M13	b ₁	1,734e+00	1,393e+01	< 2e-16
M13	b ₂	1,981e+00	3,315e+01	< 2e-16
3-параметрические модели
M17	b ₁	-1,944e+00	-1,497e+00	1,354e-01
	b ₂	9,822e-01	8,684e+00	2,220e-16
	b ₃	1,945e-02	8,249e+00	5,551e-15
M18	b ₁	2,719e+01	2,331e+01	< 2e-16
	b ₂	3,302e+00	1,562e+01	< 2e-16
	b ₃	7,451e-02	1,064e+01	< 2e-16
M19	b ₁	3,920e+01	3,769e+00	1,989e-04
	b ₂	4,426e-02	1,140e+01	< 2e-16
	b ₃	8,175e-01	7,623e+00	3,579e-13

Окончание табл. 4

№ модели	Параметр	Оценка	t-статистика	p-value
M20	b ₁	3,679e+01	5,106e+00	5,978e-07
	b ₂	2,014e-02	1,983e+00	4,828e-02
	b ₃	7,704e-01	6,930e+00	2,744e-11
M23	b ₁	3,857e+00	3,144e+01	< 2e-16
	b ₂	-3,920e+01	-3,965e+00	9,264e-05
	b ₃	1,550e+01	3,098e+00	2,143e-03

Примечание. Оценка – числовое значение параметра уравнения, t-статистика – t-критерий Стьюдента, p-value – уровень значимости для t-статистики.

Фактическая высота, м Высота, м

Обучающая выборка Тестовая выборка

Модель

Зависимость высот деревьев от диаметра ствола

Прогнозируемая высота, м

Обучающая выборка

Тестовая выборка

Модель

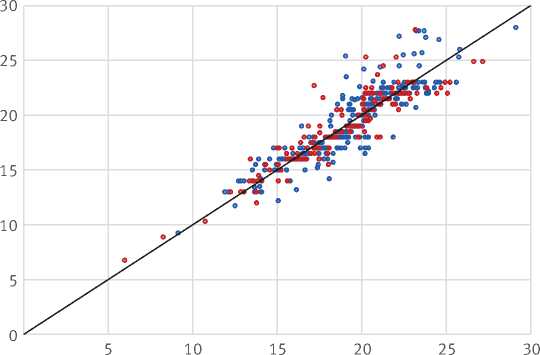
Рис. 2. Фактическая и прогнозируемая высота деревьев для обучающей и тестовой выборок

сконцентрирована вдоль диагональной линии (рис. 2).

Во многих работах показано [30, 33, 34], что лучшей прогностической способностью характеризуются модели смешанных эффектов, благодаря чему они нашли широкое применение в лесохозяйственных исследованиях. Модель смешанных эффектов (M13M) после включения в качестве случайного эффекта отдельных перечетов на пробных площадях приняла следующий вид:

h j = 1,3 + ( b1 + в i )(ln(1 + DBH )) ⁽ b ^{2 +} •"' s^ , где:

h_ij – высота дерева j из выборки i , м;
b – параметры модели;
b _i – вектор случайных эффектов для отдельного перечета из выборки i , имеющий нормальное распределение с нулевым средним и стандартным отклонением σ_b _i ;

DBH_ij – диаметр на высоте 1,3 м дерева j из выборки i , см;

ε _ij – вектор остатков, имеющий нормальное распределение с нулевым средним и стандартным отклонением σ .

Все оценки параметров и компоненты дисперсии расширенной модели имеют высокую значимость (p-значение <2e-16) (табл. 5). И модель фиксированных эффектов, и модель смешанных эффектов адекватно описали зависимость между высотами и диаметрами деревьев в дубовых древостоях. Но, как и ожидалось, первая модель имеет худшие значения метрик

Таблица 5. Итоговые оценки для модели фиксированных (M13) и смешанных эффектов (M13M)

№	Параметр	Оценка	t-статистика	p-value	Критерии качества модели
модели					RMSE	MAPE	AIC	BIC
M13	b ₁	1,927e+00	1,750e+01	< 2e-16	1,468	5,502	1513,3	1525,3
	b ₂	1,894e+00	3,975e+01	< 2e-16
M13M	Фиксированные компоненты				1,265	4,382	1259,2	1283,4
	b ₁	2,296e+00	1,079e+01	< 2e-16
	b ₂	1,756e+00	2,492e+01	< 2e-16
	Случайные компоненты
	σ_b ₁ _i	9,572e-01	-	-
	σ b 2 i	3,075e-01	-	-
	corr ( b ₁ _i ; b ₂ _i )	-9,960e-01	-	-
	σ	9,485e-01	-	-

качества по сравнению со второй. Включение случайных эффектов на уровне графика высот для отдельного перечета позволило снизить RMSE на 14 %, MAPE – на 20 %, AIC – на 17 % и BIC – на 16 %.

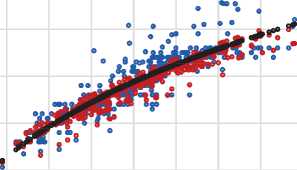
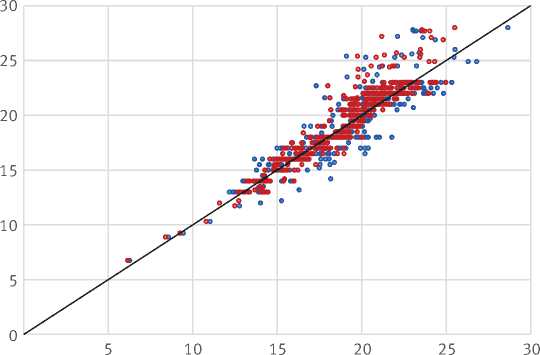
Графическая визуализация зависимости высот от диаметров по модели M13M представлена на рис. 3. Модель смешанных эффектов позволяет получить индивидуальный график высот для каждого перечета. При этом каждая кривая зависимости «высота – диаметр» характеризуется индивидуальной формой. Модель смешанных эффектов может достаточно точно прогнозировать недостающие измерения высот, но при этом стоит учитывать возможные ошибки. Это связано с наличием экстремальных выбросов (рис. 4), которые могут появляться из-за неоднородности древостоев, в том числе обусловленной действием неблагоприятных факторов окружающей среды.

Точность прогноза модели смешанного эффекта для каждого отдельного дерева сильно зависит от неоднородности древостоя и количества деревьев выборки с измеренной высотой, которые будут использоваться для прогнозирования случайных эффектов. Измеренные высоты любого количества деревьев можно

5055 60

Диаметр, см

о Фактические данные

° Прогнозируемые значения по модели смешанных эффектов

° Прогнозируемые значения по модели фиксированных эффектов

Рис. 3. Зависимость высоты деревьев от диаметра ствола по моделям смешанных и фиксированных эффектов

использовать для прогнозирования случайных эффектов, но точность во многом зависит от репрезентативности высот выбранных деревьев. Как правило, чем больше число деревьев, выбранных для прогноза случайных эффектов, тем выше будет точность прогноза модели смешанных эффектов [34].

Фактическая высота, м

Прогнозируемая высота, м

Модель фиксированных эффектов

Модель смешанных эффектов

Рис. 4. Фактическая и прогнозируемая высота деревьев для моделей фиксированных и смешанных эффектов

Заключение

Комплексная оценка метрик качества 2-и 3-параметрических моделей выявила, что лучшей обобщающей способностью характеризуются 2-параметрические модели. В качестве лучшей модели обоснована логарифмическая зависимость высот деревьев дуба от диаметров на высоте 1,3 м. Модель смешанных эффектов позволяет более точно прогнозировать значения высот по сравнению с моделью фиксированных эффектов. Недостающие значения высот большого количества деревьев на участке можно вычислить более точно с помощью модели смешанных эффектов, не применяя модель фиксированных эффектов. Использование разработанной модели должно ограничиваться только теми условиями, к которым относятся экспериментальные материалы.

Список литературы Двух- и трехпараметрические модели связи высоты деревьев с диаметром на высоте 1,3 м в дубовых древостоях

Лебедев, А.В. Верификация трехпараметрических моделей зависимости высоты от диаметра на высоте груди для березовых древостоев Европейской части России / А.В. Лебедев, В.В. Кузьмичев // Сибирский лесной журнал. - 2020. - № 5. - С. 45-54. - DOI 10.15372/SJFS20200505.
Лебедев, А.В. Проверка двухпараметрических моделей зависимости высоты от диаметра на высоте груди в березовых древостоях / А.В. Лебедев, В.В. Кузьмичев // Изв. СПбЛТА. - 2020. - № 230. - С. 100-113. - DOI 10.21266/2079-4304.2020.230.100-113.
Lebedev, A.V. New generalised height-diameter models for the birch stands in European Russia / A.V. Lebedev // Baltic Forestry. - 2020. - Vol. 26. - № 2. - P. 1-7. - DOI 10.46490/BF499.
Lebedev, A. Verification of two- And three-parameter simple height-diameter models for birch in the European part of Russia / A. Lebedev, V. Kuzmichev // Journal of Forest Science. - 2020. - Vol. 66. - № 9. - P. 375-382. - DOI 10.17221/76/2020-JFS.
Дубенок, Н.Н. Динамика лесного фонда Лесной опытной дачи РГАУ-МСХА имени К.А. Тимирязева за 150 лет / Н.Н. Дубенок, В.В. Кузьмичев, А.В. Лебедев // Изв. Тимирязевской сельскохозяйственной академии. -2018. - № 4. - С. 5-19. DOI: 10.26897/0021-342X-2018-4-5-19.
Дубенок, Н.Н. Результаты экспериментальных работ за 150 лет в Лесной опытной дачи Тимирязевской академии / Н.Н. Дубенок, В.В. Кузьмичев, А.В. Лебедев. - М. : Наука, 2020. - 382 с.
Кузьмичев, В.В. Изменение породного состава насаждений Лесной опытной дачи РГАУ-МСХА имени К.А. Тимирязева за 150 лет / В.В. Кузьмичев, А.В. Лебедев // Мониторинг состояния природных комплексов и многолетние исследования на особо охраняемых природных территориях. - 2018. - № 2. - С. 88-92.
Huxley, J. Terminology of relative growth rates / J. Huxley, G. Teissier // Nature. - 1936. - № 137. -P. 780-781.
Naslund, M. Antaletprov tradochhojdkurv ans noggrannhet / М. Naslund // Meddelanden fran Statens Skogs forskings institut. - 1929 - № 25. - Р. 93-170.
Huang, S. Development of ecoregion-based height-diameter models for white spruce in boreal forests / S. Huang, D. Price, S.J. Titus // Forest Ecology and Management. - 2000. - № 129(1). - P. 125-141.
Curtis, R.O. Height-diameter and height- diameter-age equations for second growth Douglas-fir / R.O. Curtis // Forest Science. - 1967. - № 13. - P. 365-375.
Meyer, H.A. A mathematical expression for height curves / H.A. Meyer // Journal of Forestry. - 1940. - № 38. - P. 415-420.
Wykoff, W.R. User's Guide to the Stand Prognosis Model. General Technical Report INT-133 / W.R. Wykoff, N.L. Crookston, A.R. Stage. - Stage Ogden : USDA Forest Service, Intermountain Forest and Range Experiment Station, 1982. - 231 p.
Bates, D.M. Relative curvature measures of nonlinearity / D.M. Bates, D.G. Watts // Journal of the Royal Statistical Society. Series B (Methodological). - 1980. - № 42 (1). - P. 1-25.
Staudhammer, C. Height prediction equations using diameter and stand density measures / C. Staudhammer, V. Le May // The Forestry Chronicle. - 2000. - № 76 (2). - P. 303-309.
Buford, M.A. Height-diameter relationship at age 15 in loblolly pine seed sources / M.A. Buford // Forest Science. - 1986. - № 32 (3). - P. 812-818.
El Mamoun, H.O. Modelling Height-Diameter Relationships of Selected Economically Important Natural Forests Species / H.O. El Mamoun, A.I. El Zein, M.I. El Mugira // Journal of Forest Products & Industries. - 2013. - № 2(1). - P. 34-42.
Ogana, F.N. Comparison of a modified log-logistic distribution with established models for tree height prediction / F.N. Ogana // Journal of Research in Forestry, Wildlife & Environment. - 2018. - № 10 (2). - P. 49-55.
Huang, S. Comparison of nonlinear height-diameter functions for major Alberta tree species / S. Huang, S.J. Titus, D.P. Wiens // Canadian Journal of Forest Research. - 1992. - № 22 (9). - P. 1297-1304.
Yang, R.C. The potential of Weibull-type functions as flexible growth curves / R.C. Yang, A. Kozak, J.H.G. Smith // Canadian Journal of Forest Research. - 1978. - № 8 (4). - P. 424-431.
Peng, C. Developing and validating nonlinear height-diameter models for major tree species of Ontario's boreal forests / C. Peng, L. Zhang, J. Liu // Northern Journal of Applied Forestry. - 2001. - № 18 (3). - P. 87-94.
Larsen, D.R. Height-diameter Equations for Seventeen Tree Species in Southwest Oregon / D.R. Larsen, D.W. Hann.- Corvallis : Forest Research Laboratory, Oregon State University, Corvallis, 1987.
Ratkowsky, D.A. Handbook of nonlinear regression / D.A. Ratkowsky. - New-York : Marcel and Dekker, 1990. - 241 p.
Stage, A.R. A mathematical approach to polymorphic site index curves for grand fir / A.R. Stage // Forest Science. - 1963. - № 9. - P. 167-180.
Schnute, J. A versatile growth model with statistically stable parameters / J. Schnute // Canadian Journal of Forest Research. - 1981. - № 38. - P. 1128-1140.
Атрощенко, О.А. Моделирование роста леса и лесохозяйственных процессов / О.А. Атрощенко. - Минск : БГТУ. - 249 с.
Peschel, W. Mathematical methods for growth studies of trees and forest stands and the results of their application / W. Peschel // Tharandter Forstl. Jahrb. - 1938. - № 89. - P. 169-247.
Sibbesen, E. Some new equations to describe phosphate sorption by soils / E. Sibbesen // J. Soil Sci. - 1981. - № 32 (1). - P. 67-74.
Applied Linear Statistical Models / J. Neter, M.H. Kutner, C.J. Nachtsheim, W. Wasserman. - Chicago : Irwin, 1996. - 1408 p.
Лебедев, А.В. Регрессионные модели смешанных эффектов в лесохозяйственных исследованиях / А.В. Лебедев, В.В. Кузьмичев // Сибирский лесной журнал. - 2021. - № 1. - С. 13-20. - DOI 10.15372/ SJFS20210102.
Подмаско, Б.И. Инвентаризация лиственничных лесов севера Дальнего Востока СССР методом камерального дешифрирования аэроснимков : автореф. дис. ... канд. с.-х. наук / Б.И. Подмаско. - М., 1973. - 24 с.
Хлюстов, В.К. Товарно-денежный потенциал древостоев и оптимизация лесопользования / В.К. Хлюстов, А.В. Лебедев. - Иркутск : Мегапринт, 2017. - 328 с.
Height-diametermodelsforEucaiyptussp. Plantationsin Brazil / A.C. FerrazFilho, B. Mola-Yudego, A. Ribeiro, J.R.S. Scolforo, R.A. Loos, H.F. Scolforo // Cerne. - 2018. - Vol. 24. - № 1. - P. 9-17. - DOI: 10.1590/0104776020182 4012466.
Sharma, R.P. Nonlinear mixed effect height-diameter model for mixed species forests in the central part of the Czech Republic / R.P. Sharma, Z. Vacek, S. Vacek // Journal of Forest Science. - 2016. - № 62 (10). - P. 470-484. DOI: 10.17221/41/2016-JFS.

Еще

Статья научная