Двухкомпонентная стеганографическая система на основе отношения линейных функций двух сигналов с размещением информативного сигнала в знаменателе функции встраивания сообщения

Повышение эффективности существующих стеганографических систем сопряжено с совершенствованием существующих алгоритмов и разработкой новых подходов к формированию стеганографических контейнеров [1–10]. В статье рассматривается алгоритм формирования двухкомпонентного стеганографического контейнера и проводится его исследование. Целью исследования является поиск условий достижения максимальной чувствительности системы к погрешности значений ключевых коэффициентов. В рамках статьи показывается влияние погрешности значений ключевых коэффициентов на частотный спектр сигнала контейнера.

Двухкомпонентная инвариантная стеганографическая система в общем случае описывается выражениями:

ui (n )=fi (u (n));

. u 2 ⁽ n ) = f - ( u ⁽ n ) ) ;                      (1)

yi (n)- fз (ui (n), ^( n )) = 0;

_У2 (n)- f 4 (u2 (n), ^(n)) = 0, где u1 и u2 – встраиваемые в двухкомпонентный контейнер сигналы, являющиеся функциями сигнала сообщения u; ^ - маскирующий сигнал; y1 и y2 – компоненты двухкомпонентного стеганографического контейнера; n – счетчик отсчетов.

При таком подходе компоненты будут отличаться друг от друга, а выражение извлечения будет инвариантно от маскирующего сигнала.

Подсистема встраивания сообщения определяется как

У1 (n )=fз (и (n), E( n));

_ У 2 ( n ) = f 4 ( u 2 ( n ) , ^E ( n ) ) •

Подсистема извлечения описывается выражением:

u ( n ) = f ( У 1 ( n ) , У 2 ( n ) ) .            (3)

В работе [1] рассматривается математическая модель алгоритма встраивания на основе отношения линейных функций двух сигналов. Общий вид выражения, представляющего собой отношение линейных функций двух сигналов, имеет вид

1 + аи,

У =      ¹

b + cu ₂

.

В работе [1] в качестве информативного сигнала выступает и 1 , а в качестве маскирующего сигнала - и ₂, то есть информативный сигнал размещен в числителе функции встраивания сообщения. В данной статье рассматривается другой подход, когда информативный сигнал размещается в знаменателе функции формирования контейнера.

Математическая модель стеганографической системы

Рассмотрим вариант, когда в роли маскирующего сигнала выступает сигнал и 1 . В этом случае компоненты контейнера будут иметь вид

1 + а , Е

• У 1 =     —;

b 1 + c 1 и 1

• 1    + а ₂ Е

У 2 — ГТ---, b 2 + c 2 и 2

где a, b и c – коэффициенты (5) .

Рассмотрим два варианта формирования сигналов u ₁ и u ₂ через сигнал сообщения.

Аддитивная связь:

u 1 — и ;

и ₂ — K - и 1 .

Мультипликативная связь:

u 1 — и ;

и ₂ — и 1 / K.

Решая систему (5) с учетом (6), получим выражение для извлечения сигнала сообщения для первого варианта:

_ а1 - а 2 - а1 b2 У 2 + а 2 b У1 - а1 c 2 У 2 K и — и —--. (8)

а 1 c 2 У 2 + а 2 с 1 У 1

Решая систему (5) с учетом (7), получим выражение для второго варианта:

и — и — к -a , + a 2 + a , b 2 ^У 2 - a 2 ^Ь , ^У , .     (9)

а ₂ с 1 У 1 K - а 1 c ₂ у ₂

Исследование

Выражения (5) представляют собой дроби, причем в числителе находится маскирующий сигнал Е . Таким образом, искажение маскирующего сигнала при встраивании сообщения определяется знаменателем функции. Очевидно, что это искажение нелинейно и определяется степенью отличия знаменателя от единицы. При выборе коэффициентов следует учитывать, что увеличение значения коэффициента c приведет к снижению маскирующих свойств алгоритма. Коэффициенты a и b должны быть одного порядка, что позволит сохранить амплитуду заполненных контейнеров близкой к амплитуде маскирующего сигнала Е .

Максимальная чувствительность стеганографической системы достигается вблизи точки разрыва функции извлечения информативного сигнала. Заметим, что y ₁ и y ₂ представляют собой дроби. Поэтому знаменатель функции извлечения не позволяет определить точку разрыва функции. Для определения точки разрыва функции извлечения требуется подстановка в функцию извлечения выражений (6) и (7), после чего определять точку разрыва. В результате преобразований определено условие максимальной чувствительности функций извлечения информативного сообщения.

Для связи (6) и функции извлечения (8):

c 2 ^{— —} b 2 c 1 / b 1 + c 1 K ,

< a ₂ — a 1 + о                       (10)

при о^ 0.

Причем при значении и 1 , равном:

^и 1 ^— —¹ ,                 ⁽¹1)

c ₁ возникает разрыв функции извлечения, то есть это соотношение недопустимо.

Для связи (7) и функции извлечения (9):

b 1 c 2 - b 2 c 1 к — 0;

< а ₂ — а 1 + о                     (12)

при о^ 0.

Условие (11) справедливо и для данного варианта.

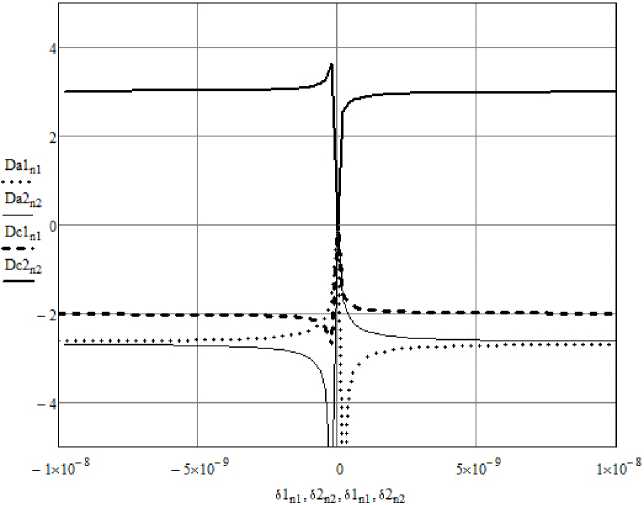
Рисунок 1. Зависимость ошибки извлечения сигнала от вариации коэффициентов a и с

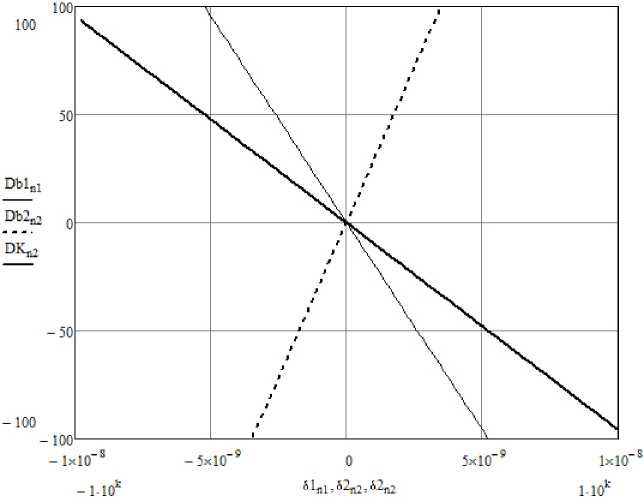
Рисунок 2. Зависимость ошибки извлечения сигнала от вариации коэффициентов b и K

Чувствительность выражений извлечения (8) и (9) к вариации коэффициентов определяется через дифференциал, а после перехода к приращениям коэффициентов имеет вид

A = D A + D A + D, A, + u1         a1a1         a2a2         b1b1

+ D, A, + D A + D A + DKAK.

b 2 b 2        c c       c 2 c 2        K K

Проведем численное исследование ошибки извлечения значения u ₁ с помощью выражения (13) от вносимой погрешности в различные коэффициенты преобразования. Для алгоритма с аддитивной связью (6) результат численного исследования приведен на рисунках 1 и 2.

Для численного эксперимента выбрано значение информативного сигнала u 1 = 2, таким образом, вариация любого коэффициента приводит к ошибке, соизмеримой со значением информативного сигнала, причем нарастание ошибки выше для коэффициентов a и c . Однако этих данных недостаточно, чтобы определить, какой коэффициент может быть использован в роли ключевого, так как важен характер вносимого искажения в динамике. Проведем численный эксперимент, иллюстрирующий искажение извлекаемого сигнала во времени при вносимой в значение коэффициентов погрешности.

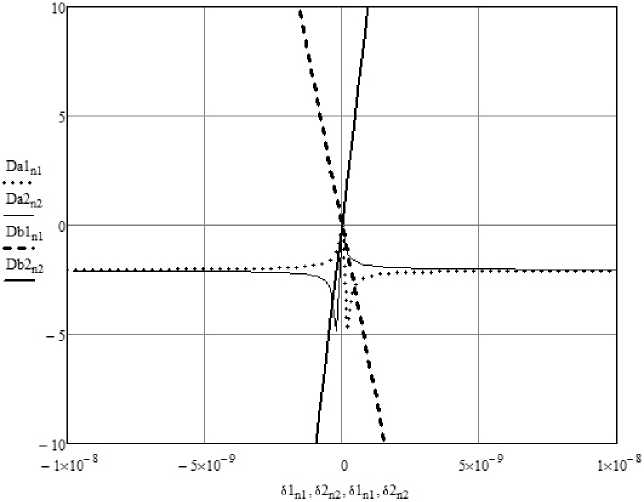
Рисунок 3. Зависимость ошибки извлечения сигнала от вариации коэффициентов a и b

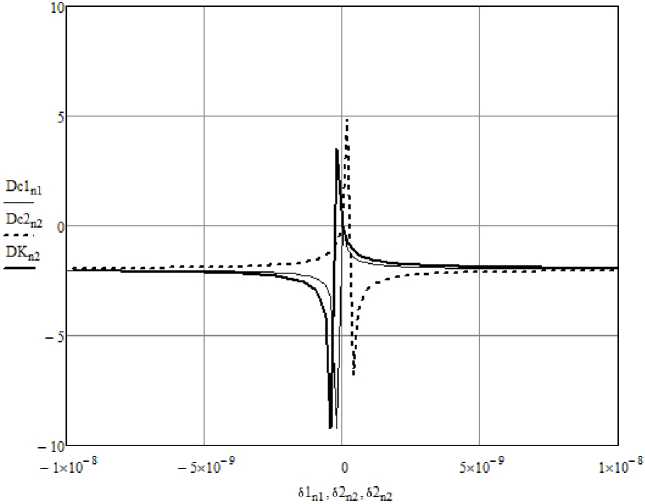
Рисунок 4. Зависимость ошибки извлечения сигнала от вариации коэффициентов c и K

Для алгоритма с мультипликативной связью (7) результат численного исследования приведен на рисунках 3 и 4.

Важным аспектом сокрытия сигнала является его маскировка в частотном спектре. Внесение погрешности в значение коэффициентов может приводить к амплитудной ошибке извлечения с сохранением формы спектра, а может значительно искажать спектр. Численные исследования показали, что для алгоритма на основе аддитивной связи встраиваемых сигналов (6) наиболее заметное искажение спектра возникает в извлекаемом сигнале при внесении погрешности в коэффици- ент a1. Проведем эксперимент, иллюстрирующий зависимость изменение спектра извлекаемого сигнала от вносимой погрешности. На рисунке 5 приведена поверхность, показывающая изменение спектра восстановленного сигнала от ошибки δ⋅1012 в значении коэффициента a1 от изменения δ. Видно, что при нулевой ошибке спектр состоит из одной гармоники. При увеличении ошибки гармоника информативного сигнала скрывается в спектре маскирующего сигнала.

Отметим, что при σ= 10 ^{- 9} и ошибке значения a ₁ = 15 ⋅ 10 ^{- 11} гармоника информативного сигнала

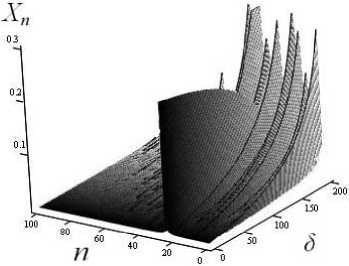
Рисунок 5. Зависимость спектра восстановленного сигнала от ошибки, внесенной в коэффициент a ₁

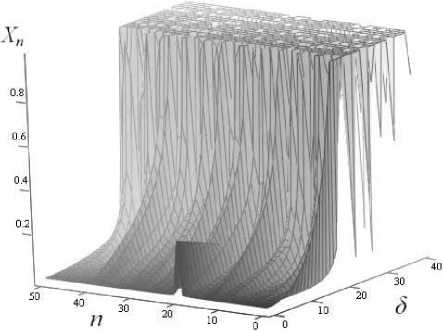
Рисунок 6. Зависимость спектра восстановленного сигнала от ошибки, внесенной в коэффициент c ₁

полностью скрывается в спектре маскирующего сигнала.

Для алгоритма на основе мультипликативной связи встраиваемых сигналов (7) наиболее заметное искажение спектра возникает в извлекаемом сигнале при внесении погрешности в коэффициенты a и b . Проведем эксперимент, иллюстрирующий зависимость изменения спектра извлекаемого сигнала от вносимой в коэффициент a ₁ погрешности. На рисунке 6 приведена поверхность, показывающая изменение спектра восстановленного сигнала от ошибки δ⋅ 10¹¹ в значении коэффициента a 1 от изменения 8 . Видно, что при нулевой ошибке спектр состоит из одной гармоники. При увеличении ошибки гармоника информативного сигнала скрывается в спектре случайного сигнала.

Проведем эксперимент, иллюстрирующий зависимость изменения спектра извлекаемого сигнала от вносимой в коэффициент b ₁ погрешности. На рисунке 7 приведена поверхность, показывающая изменение спектра восстановленного сигнала от ошибки δ⋅ 10¹¹ в значении коэффициента Ь 1 от изменения 8 . Видно, что при нулевой ошибке спектр состоит из одной гармоники. При увеличении ошибки гармоника инфор-

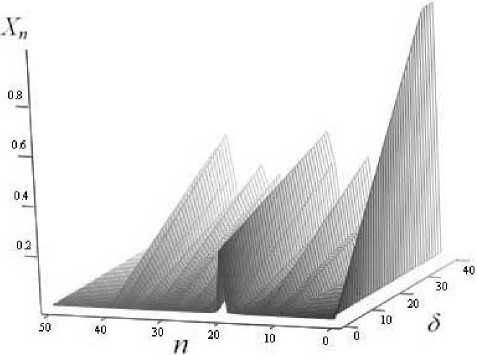
Рисунок 7. Зависимость спектра восстановленного сигнала от ошибки, внесенной в коэффициент b ₁

мативного сигнала скрывается в спектре случайного сигнала.

Отметим, что при σ= 10 ^{- 9} и ошибке значения b ₁ = 40 ⋅ 10 ^{- 11} гармоника информативного сигнала скрывается в спектре маскирующего сигнала. Очевидно, что использование коэффициента a в качестве ключевого, позволяет получить лучшие результаты маскировки сообщения. Таким образом, в предлагаемом алгоритме коэффициенты a рекомендуются к использованию в качестве ключевых коэффициентов.

Выводы

Полученные в статье результаты на порядок превосходят результат в работе [1]. Так, в работе [1] маскировка спектра сообщения в спектре маскирующего сигнала достигается при вносимой в ключевой коэффициент погрешности 8 - IO ^{- 10}. В то время как размещение информативного сигнала в знаменателе функции извлечения позволяет обеспечить маскировку спектра сообщения в спектре маскирующего сигнала при вносимой в ключевой коэффициент погрешности 15 - 10 ^{- 11}.

Рассмотренный алгоритм формирования двухкомпонентной инвариантной стеганографической системы является более устойчивым к взлому за счет высокой чувствительности к вариации ключевого коэффициента. Свойство инвариантности двухкомпонентной системы [1–10] позволяет встраивать сигналы u ₁ и u ₂ значительно меньшей амплитуды, нежели маскирующий сигнал £ , и не позволяет эффективно обнаружить замаскированное сообщение слепым применением функции извлечения за счет высокой чувствительности функции извлечения скрытого сигнала к вариации ключевого коэффициента.