Двухмассовый маятник

Для сообщения инертному телу периодических возвратно-поступательных движений требуется затрата соответствующим образом изменяющейся энергии. Это обусловлено тем, что тело обменивается энергией с приводом.

Целью работы является создание осциллятора, не нуждающемся в обмене энергией с приводом.

В классических осцилляторах свободные синусоидальные колебания сопровождаются обменом энергии между его элементами, имеющими противоположный характер реактивности [1-3].

В пружинном маятнике груз обменивается энергией с пружиной.

В электрическом колебательном контуре катушка индуктивности обменивается энергией с конденсатором.

Известны колебательные системы, в которых груз или пружина обмениваются энергией с катушкой индуктивности или кондесатором [4-6].

Все указанные колебательные системы по существу являются биреактивными , а именно: m-k, L-C, m-L, m-C, k-L, k-C .

Свободные синусоидальные колебания могут возникать при взаимной трансформации каких угодно физических видов энергии [7].

Это обстоятельство является побудительным мотивом создания осциллятора, в котором свободные синусоидальные колебания сопровождаются трансформацией кинетической энергии инертного элемента в кинетическую же энергию другого инертного элемента. Элементы с другим характером реактивности в таком осцилляторе отсутствуют.

Такой осциллятор по существу является монореактивным , а именно: m-m .

Актуальность исследования определяется тем, что периодические процессы имеют повсеместное применение [8-10].

Синтез осциллятора производится на основе трех предпосылок.

Первое . Осциллятор состоит из двух одинаковых по массе грузов.

Второе . Грузы совершают синусоидальные перемещения

Х1 = A sin (z + Z1), x2 = A sin (Z + Z2 ) .

Здесь X ], x₂ - перемещения инертных элементов, A - амплитуда, Z — изменяющаяся фаза колебаний, Zi , Z2 — начальные фазы колебаний.

Третье . Суммарная энергия осциллятора со временем не изменяется W_x + W, = const .

Из второй и третьей предпосылок следует

m f dL Y 2 ( dt )

m

+

2

(dx2 )2

V dt 7

= const,

cos2 (Z + Zi) + cos2 (Z + Z2 ) = const.

Из второго выражения следует, что n

Z1 +Z 2 = ±^

Эта формула дает возможность определить конфигурацию монореактивного гармонического осциллятора, которая представлена на рисунке.

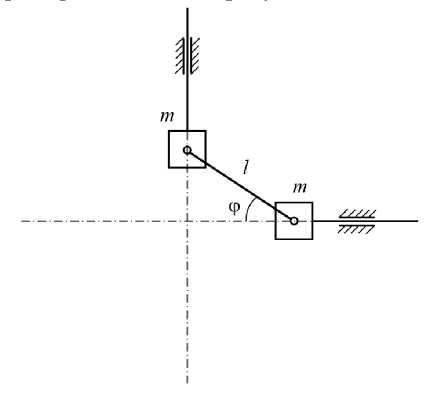
Рис. 1. Монореактивный гармонический осциллятор

Анализ осциллятора

Допущения . К инертным элементам внешние силы не приложены. Масса соединительного элемента равна нулю. Потери на трение отсутствуют.

В соответствии с рисунком перемещения инертных элементов имеют вид:

X = l cos ф,

x2 =lcos

Текущая фаза ф наилучшим образом подходит на роль обобщенной координаты.

Рассматриваемая механическая система обладает одной степенью свободы, поэтому, соответственно, уравнение Лагранжа второго рода принимает следующую форму:

d (дТ)  дT

-^

dt (дф J  дф

Так как активные силы равны нулю, то обобщенная сила тоже равна нулю Q = 0 .

Суммарная кинетическая энергия системы равна

m ( dx. Т 2 ( dt )

m ( dx, + — —-

2 ( dt

ml2          ml2           ml2

—— sin фф + —— cos фф = —— ф .

Отсюда следует

дт     дт г. d (ат)    2„

— = 0, — = ml ф , — — = ml ф = 0.

дф     дф        dt (дф)

Это дифференциальное уравнение имеет элементарное решение

d ф

—— = C1, ф = C1t + C2.

dt

Постоянные интегрирования С 1 и С 2 находятся с учетом начальных условий ф ⁽⁰⁾ = ф о ,

d ф zm — (0) = ©o.

dt

Отсюда следует

C 1 =^ 0 , C 2 =ф о .

С учетом установленных величин перемещения инертных элементов (1) и (2) приобретают вид:

X = l cos («„ t + ф0),

П

x2 = l cos —

-toot -фо I.

Если исходное положение первого инертного элемента равно

X1(0) = X10 , то

x

cos фо = -10,

ф0 = arccos — = arcsin x20.

Если исходная скорость второго инертного элемента равна

dx

• -72 (0) = v 20 , dt

  то

  
  

ltoo cos (too0 + Фо ) = v20 , v20      v10

—--—--

x 10      x 20

С учетом полученных выражений перемещения инертных элементов и их скорости можно записать в виде:

lvx

± cos — t + arccos — , xl

П    V ,A

X. — l cos — + —101

^-

2

x 20

x

arcsin^° ,

v

v — l —10-sin x20

—t + arcsin — , 720              l у

vx

cos ^° t - arccos^0- .

v ₂ — lv 20 x 10

Заключение. В монореактивном ( m-m ) гармоническом осцилляторе инертные элементы могут совершать свободные синусоидальные колебания, которые сопровождаются трансформацией кинетической энергии инертного элемента в кинетическую же энергию другого инертного элемента.

В положении, при котором ф — 0 энер- гия первого инертного элемента равна нулю. При этом энергия второго элемента имеет максимальное значение. В следующий момент времени первый элемент приобретает ускорение за счет кинетической энергии второго элемента, скорость которого начинает уменьшаться.

В соответствии с выражениями (3) – (8) в монореактивном ( m-m ) гармоническом осцилляторе могут возникать свободные гармонические колебания любой заданной частоты, которая определяется исключительно начальными условиями.