Двухмерная модель "цветения воды" в водохранилище равнинного типа

Институт экологии Волжского бассейна РАН, г. Тольятти

На основе уравнений Вольтерра построена математическая модель с учетом диффузии по пространству, позволяющая объяснить процесс возникновения "волны цветения" с весенним и осенним пиками.

В предыдущих работах авторов [1, 2] дано описание оригинальной модели воль-терровского типа процесса "цветения воды" (массового развития фитопланктона ‒ до 100 и более мг/л) в равнинных водохранилищах:

dx1/dt = α1x1P ‒ r12x1x2, dx2/dt = α2x2P ‒ r21x1x2 ‒ γx2z, dz/dt = γx2z ‒ α3z ‒ σ1zM,       (1)

dP/dt = ξP ‒ β1x1P ‒ β2x2P, dM/dt = ξM ‒ σ2zM , где x1 и x2 ‒ концентрации "обычных" (зеленые, протококковые, диатомовые, эвгленовые и др.) и синезеленых водорослей, z ‒ концентрация зоопланктона, α1 и α2 ‒ коэффициенты экспоненциального роста "обычных" и синезеленых водорослей, α3 ‒ коэффициент экспоненциального вымирания зоопланктона, r12 и r21 ‒ коэффициенты межвидовой конкуренции, γ ‒ коэффициент "переработки" биомассы зеленых водорослей в биомассу зоопланктона, Р ‒ концентрация в воде биогена (например, фосфора), β1 и β2 ‒ скорости "выедания" этого биогена водорослями, ξP ‒ постоянное количество сбрасываемого в воду биогена за единицу времени, М ‒ концентрация в воде тяжелых металлов, σ1 и σ2 ‒ коэффициенты "потребления" тяжелых металлов зоопланктоном, ξM ‒ постоянное количество сбрасываемых в воду тяжелых металлов за единицу времени. При этом, коэффициент α2, строго говоря, зависит от температуры воды Т. Температура воды в каждой точке равнинного водоема определяется, в основном, ветровым перемешиванием и режимом

"сработки" водохранилищ, поэтому ее можно определять (в самом простом варианте) по уравнению линейной регрессии и для простоты считать:

0, Т < Т 0

α 2 =

α 0 , Т ≥ Т 0 .

где Т0 ‒ граничное значение температуры, после которой начинается активное развитие синезеленых водорослей.

Проведенный анализ этой "нульмерной" модели позволил в рамках данных гипотез о взаимодействии биотических и абиотических компонент системы описать механизм возникновения пиков "цветения воды" весной и осенью, вскрыть некоторые особенности "поведения" тяжелых металлов и биогенов в водоеме. При этом (рис.1) данную модель можно с высокой степенью качественной адекватности [3, 4] считать весьма удовлетвори-

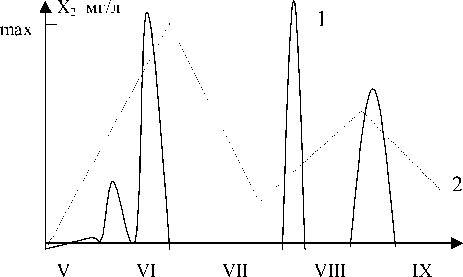
X

Рис.1. Зависимость биомассы синезеленых водорослей (х2) от времени (t) по результатам моделирования (1) и по наблюдаемым данным на Ульяновском плесе Куйбышевского водохранилища в 1982г. (данные нормированы на максимум биомассы)

тельной для описания феномена "цветения воды", который хорошо прослеживался по данным ИЭВБ РАН [5, 6].

Для описания динамики в системе "ресурс ‒ потребитель" предлагается следующая "линеаризация" модели [7] (потребитель считается неподвижным, ресурс ‒ не возобновляемым):

dR/dt = v dR/dx + D d2R/dxdx ‒ V(R)N, dN/dt = V(R)N ‒ mN, (2)

где R и N ‒ концентрации ресурса и потребителя соответственно, v ‒ скорость течения реки, D ‒ коэффициент адвективной диффузии, V(R) ‒ трофическая функция, m ‒ коэффициент естественной смертности потребителя. Иными словами, в модели (2) учитывается диффузия вещества по одной пространственной координате (такого рода модель должна качественно адекватно описывать динамику системы (1) в "узких" и "длинных" водохранилищах; примерами таковых в Волжском бассейне могут служить Саратовское и Волгоградское).

Наблюдениями гидробиологов (см., например, [8]) показано, что для "широких" и "длинных" водохранилищ (например, Куйбышевское) имеет место феномен, который можно определить как "волну цветения" по пространству водохранилища. Для объяснения механизма этого феномена предлагается следующим образом модифицировать модель (1).

Рассмотрим квадрат [0,Y] * [0,Y]. Уравнение переноса и турбулентной диффузии гидрозоля (в двухмерном варианте и при постоянном коэффициенте диффузии D) имеет следующий вид [9]:

dФ/dt ‒ D ∆Ф + σ0 Ф + vx dФ/dx + + vy dФ/dy = Q w(r ‒ r0) , dv/dx + dv/dy = 0 , где Ф ‒ концентрация загрязняющего гидрозоля, w(r ‒ r0) ‒ функция источника, r = r(x,y) , Q ‒ мощность источника, r0 ‒ точка предполагаемого стока, v ‒ скорость течения по координатам х и у . Будем считать, что сброс гидрозоля идет с берегов водоема равномерно по всей их длине [0, Y]. Тогда функция ис- точника имеет вид:

w(r ‒ r 0 ) =

ζ , у = 0, Y

0 , 0 < y < Y .

Начальные условия: Ф(0, х, у) = Ф0(х, у), граничные условия на верхнем "срезе" течения: Ф(t, 0, y) = Ф0(t) , dФ(t, 0, y)/dx = q(t) , на берегах заданы "условия непротекания": dФ(t, x, 0)/dy = dФ(t, x, Y) = 0 .

С учетом этих соотношений итоговая система уравнений будет выглядеть следующим образом:

dx₁/dt = α ₁x₁P ‒ r₁₂x₁x₂ + D ∆ x₁ ‒

‒ σ0x1 ‒ vy dx1/dy ‒ vx dx1/dx , dx2/dt = α2x2P ‒ r21x1x2 ‒ γx2z +

+ D ∆ x₂ ‒ σ ₀x₂ ‒ v_y dx₂/dy ‒ v_x dx₂/dx , dz/dt = γ x₂z ‒ α ₃z ‒ σ ₁zM + D ∆ z ‒

‒ σ ₀z ‒ v_y dz/dy ‒ v_x dz/dx ,             (3)

dP/dt = ξ _P ‒ β ₁x₁P ‒ β ₂x₂P +

+ D ∆ P ‒ σ ₀P ‒ v_y dP/dy ‒ v_x dP/dx , dM/dt = ξ _M ‒ σ ₂zM + D ∆ M ‒

‒ σ0M ‒ vy dM/dy ‒ vx dM/dx , где vx и vу ‒ компоненты вектора скорости v .

Соответствующим образом задаются начальные условия:

х1(0,х,у) = х10(х,у); х2(0,х,у) = х20(х,у);

z(0,x,y) = z0(x,y); P(0,x,y) = P0(x,y);

M(0,x,y) = M0(x,y);

и граничные условия:

x1(t,0,y) = x10; dx1(t,0,y)/dx = qx1;

dx1(t,x,0)/dy = 0;

x2(t,0,y) = x20; dx2(t,0,y)/dx = qx2;

dx2(t,x,0)/dy = 0;

z(t,0,y) = z0; dz(t,0,y)/dx = qZ;

dz(t,x,0)/dy = 0;

P(t,0,y) = P0; dP(t,0,y)/dx = qP;

dP(t,x,0)/dy = 0;

M(t,0,y) = M0; dM(t,0,y)/dx = qM;

dM(t,x,0)/dy = 0;

Аппроксимация уравнений (переход от непрерывных уравнений в частных произ- водных к дискретным) и оценка устойчивости схем осуществлялась по [10]. По пространственным координатам интегрирование велось по 25 точкам, по временной - по 100 (фактически, охватывался весь вегетационный период развития фитопланктона).

При расчетах проводилась проверка на точность: первоначально численное интегрирование велось с одним шагом по времени; затем шаг уменьшался вдвое и вычислялись нормы решения с обычным шагом и разности двух решений. Если норма разности решений превышала 5% от нормы решения с обычным шагом, новый шаг по времени принимался в два раза меньшим и процедура проверки на точность повторялась. Расчеты проводились при двух наборах коэффициентов, которые различались лишь в следующем: по сравнению с первым при втором режиме в модели (3) коэффициент роста биомассы жертвы-фитопланктона ( а ₂) увеличен на 25% (синезеленые водоросли растут более интенсивно).

На рис.2 показано распределение плотности популяции синезеленых водорослей (х2) через одни сутки после начала интегрирования при первом режиме. Наблюдаемая картина почти полностью совпадает с начальной. С течением времени (через 40 точек-су-ток) вдоль оси Х образуется волна, которая начинает распространяться по пространству и через 80 точек-суток становится вполне заметной (рис.3). Аналогичная, но более "яркая", картина наблюдается при моделировании второго режима (рис.4 и 5). При этом, первоначально появляющийся пик не дости-

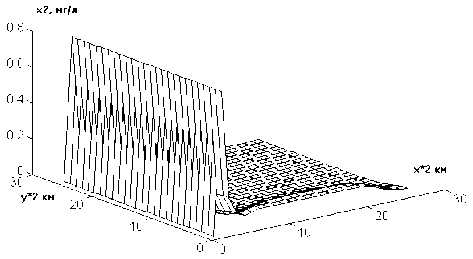
Рис.3. Зависимость концентрации синезеленых водорослей от пространственных координат при значении времени t = 100 сут гает начальных значений концентрации, но по мере движения "волны" концентрация синезеленых водорослей доходит до 5 мг/л, что по ГОСТ 17.1.01-77 принято за "умеренное цветение вод" [11].

Так как "цветение вод" чаще всего связывается с поступлением в водоемы биогенов (чаще всего, фосфоросодержащих), интересно посмотреть динамику именно этой (Р) переменной модели (3). На рис.6 показан результат моделирования, который отличается от первого режима тем, что на "поднятии" концентрации биогена вдоль берегов (последнее объясняется его диффузионным смывом) наблюдается небольшая выемка, объясняемая поглощением биогена развивающимися синезелеными водорослями. При моделировании "интенсивного" (10-100 мг/л) или "гиперцветения" (более 100 мг/л) следует ожидать более заметного воздействия синезеленых водорослей на концентрацию биогенов.

Таким образом, предложенная модель (3) позволяет объяснить и явление "цветения воды" (весенние и осенние пики), и "волну

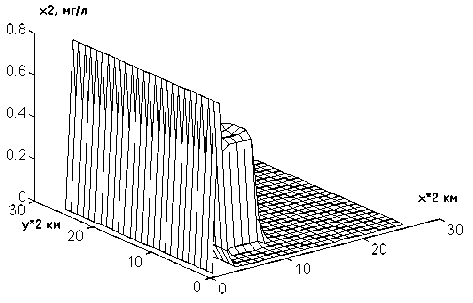
Рис.2. Зависимость концентрации синезеленых водорослей от пространственных координат при значении времени t = 1 сут

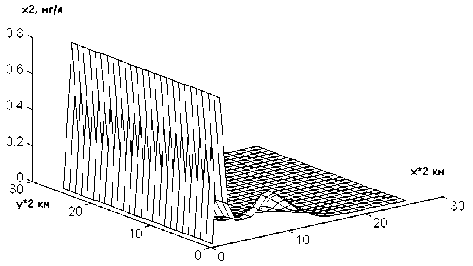
Рис.4. Зависимость концентрации синезеленых водорослей от пространственных координат при значении времени t = 50 сут и α₀ = 1250

х2, мг/л

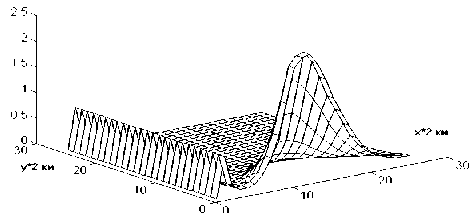
Рис.5. Зависимость концентрации синезеленых водорослей от пространственных координат при значении времени t = 90 сут и α₀ = 1250

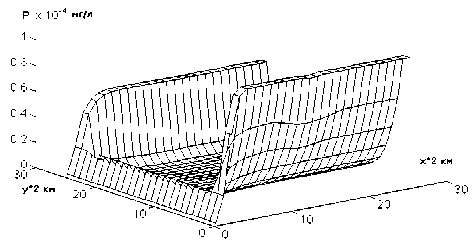
Рис.6. Зависимость концентрации фосфора от пространственных координат при значении времени t = 100 сут и α₀ = 1250

цветения" по поверхности водоема. Заключенный в модель механизм отличается от принятого в гидробиологии механизма евт-рофикации (в основном, через воздействие только биогенов) большей "реалистичностью", что делает его полезным как для целей объяснения наблюдаемых феноменов, так и для синтеза на его основе сложных прогнозирующих имитационных моделей.