Двухпараметрический метод эквивалентных масс

В общем случае при вычислении ФСП ^_Др необходимо выделять вклады в поглощение, обусловленные крыльями отдаленных СЛП атмосферных газов т_Ду, ИДП т_Ду, селективным поглощением т Д _у СЛП, входящих в выбранный спектральный интервал ( вследствие различий в этих случаях зависимости пропускания τ от содержания поглощающего газа w, давления Р и температуры Т). Подобное разделение позволяет существенно улучшить точность вычисления Т д _у и расширить область достоверности функции т_Ду(ш, Р) по содержанию поглощающего газа и давлению.

Тогда для заданного компонента:

kис τ = τ ⋅ τ ⋅ τ , Δ ν     Δ _ν Δ _ν Δ _ν

функция т A v • тA v = exp[-(вуk (T) + Pv„ (T))»P] . (16) где eVk(^) и вук(^) — коэффициенты континуального и индуцированного давлением поглощения, зависящие только от температуры.

Для получения ФСП T ^ _vв атмосферах планет и высокотемпературных средах, давление в которых изменяется в широких пределах, в предложен двухпараметрический метод эквивалентной массы.

При вычислении т^в общем случае справедливо уравнение:

I ln т A v J

I ln ^ v J

+

1пт a c

V ^{111 L}A v J

M

⁽ ln т А v Iln T l v ) ’

где т Acv = exp[— kv T )®],                      (18)

определяет ФСП при повышенных давлениях (Р > 10атм) в условиях «вращательной» структуры СП:

тAv = exp [ - P v ( T ) » m ^v Р Э^v ] ,                  (19)

ФСП при малых давлениях Р < 1 атм. Параметр М характеризует изменение скорости роста ФСП при переходе от области слабого поглощения в область сильного поглощения. Параметры Kv, mv, nv, PVc, M определяются из экспериментальных данных. В соответствии с теорией модельного представления спектров поглощенияуравненияК = S/d определяет отношение средней интенсивности к расстоянию между линиями, а величина /^Дт характеризует интенсивность группы СЛП, расположенных в выбранном интервале Дтл Для расчета Тду в условиях неоднородной по температуре и давлению атмосферы удобно ввести температурные функции:

• F1" (t )=K""^ ’ F2" (t)=Hrl ■

^K v ( T O )             ^ev _c ( T O )

Тогда

• - In T1Cv = Kvc (To )W; - In Tc = pvc (To W2,(21)

где

W1 = ( p(lF1 c [l (T )¥l,(22)

l

W2 = fp(lXP(l)/Po)nv/mvF^cmv [l(T)]dl ,(23)

l

Аналогично, для индуцированного и континуального поглощения

Pvи = Pvи (To )Fu (T),Pvk = Pvk (To)Fk (T).(24)

Используемые для расчетов температурные функции F_u(l"), F_k(T), F ic (T'), F_2c(T) могут быть представлены в табличной форме или в виде простых аналитических аппроксимаций, например, в экспоненциальной или степенной форме.

Соотношение (19) является наиболее простой аппроксимацией для ФСП в области работы «сильного поглощения». В общем случае зависимость от W ФСП в области сильного поглощения зависит от структуры спектра и аналитическая зависимость т дС может быть выбрана и в другой форме. В работе [24] предложено аппроксимировать т'v в виде произведения двух функций, зависящих от одной эквивалентной массы т'С = exp [-ev(T)»mvРэv J.[1 -Ф^cгоmvРэ"v )] ,     (25)

где O (3 _v го ^mv Р э ^nv ) - интеграл вероятности ошибок.

В аппроксимации (25) сильного поглощения скорость роста ФСП для заданной величины (Рлс + Рл c) зависит от соотношения параметров вЛс и Рлс • Входящие в расчетные формулы (4.23–4.34) параметры были определены для различных температур Т в полосах паров H2O, CO2, N2O, CO, NO, O3,

HCl, HNO 3 , NH 3 , CH 4 , NO 2 , C 2 H 2 , C 2 H 4 .

Для простых молекул CO, NO, HCl, HF при Т< 900 К сильная аппроксимация описывается интегралом вероятности ошибок. Для молекул CO ₂ , NO ₂ вклады, обусловленные экспоненциальной формулой и интегралом вероятности ошибок, зависят как от типа полосы, так и от выбранного участка спектра.

Наилучшая подгонка параметров, входящих в расчетные формулы при их нормировке на экспериментальные данные, обсужденные в [8]–[12], [23], [24], [80], приводит к ошибкам в расчетных значениях Ат_Др< 3 ^ 4% ,что не превосходит ошибок измерений ФСП. При использовании точных данных по ФСП, полученных МЧИ тонкой структуры СП, подгонка под аппроксимации показала, что ошибки вычислений   At_Av <2^3%.

Последнее свидетельствует, что двухпараметрический метод эквивалентной массы позволяет выполнить корректные расчеты ФСП и улучшить точность вычислений ФСП по сравнению с однопараметрическим методом эквивалентной массы

в 2–3 раза.

Двухпараметрический метод эквивалентной массы приемлем при решении задач переноса излучения в атмосферах планет и при решении задач радиационного теплообмена в энергетических установках, если темпера-турный профиль в среде не претерпевает резких инверсий и градиентов. На рис. 4.1–4.5 приведены сопоставления вычисленных и измеренных спектров поглощения, подтверждающие хорошую точность расчета ФСП по эмпирическим методикам, развитым авторами и МЧИ.

Наиболее простой формой учета влияния температуры на функцию т^(П является определение аппроксимаций температурных функций Г^с и Г2с в формулах. При этом необходимо принимать во внимание и то обстоятельство, что с изменением условий в атмосферах могут перераспределяться степени влияния различных факторов на ФСП. Поэтому эмпирические температурные функции всегда имеют ограниченную область применения. Наиболее простым и гибким являются экспоненциальностепенные зависимости температурных функций

( т K o

Fc ^{( T} ) = Y

V To J

exp K 1 ( T - T 0 ) K ²

K ₃

V ToJ

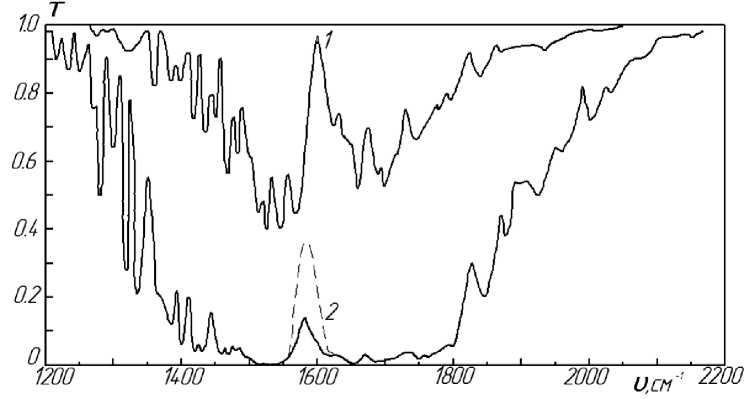
Рис. 1. Сравнение измеренных (–) и вычисленных МЧИ (- - -) спектров поглощения

в полосе 6,3 мкм паров Н 2 О. го_Н2О,г.см ²:1 — 0,002; 2-0,1; Р Э = 1 атм.

Параметры Ko(y) , K-(y) ,K2(y) , K3(y) являются параметрами подгонки под экспериментальные данные.

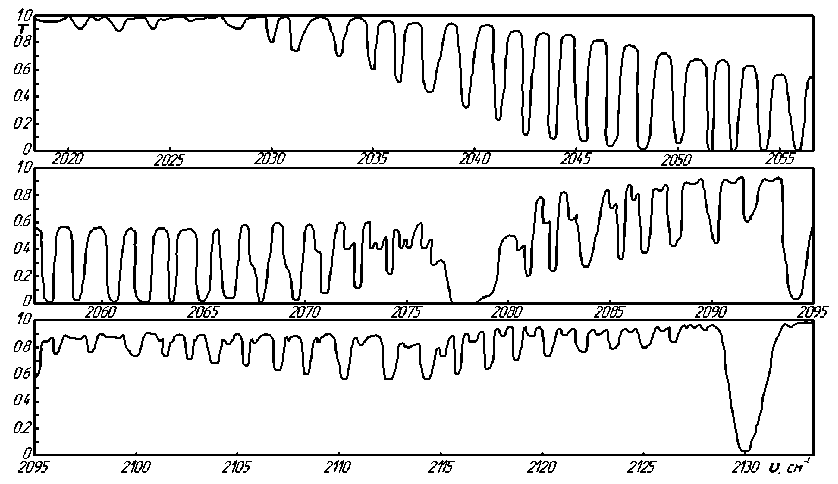
Рис. 2. Сравнение измеренного с высоким разрешением (—) и (. . .) МЧИ спектров поглощения в окрестности полосы 4,8 мкм СО2 при температуре Т = 300 К

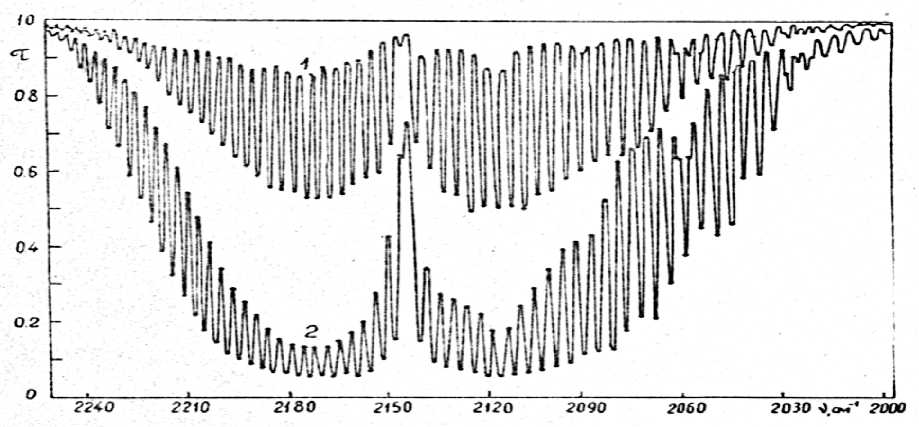
Рис. 3. Сравнение измеренного (—) с разрешением Д=1 см 1 и вычисленного МЧИ (. . .)

спектров поглощения в основной полосе СО для содержаний ω = 0,63 и 10 см атм при Т = 300 К.

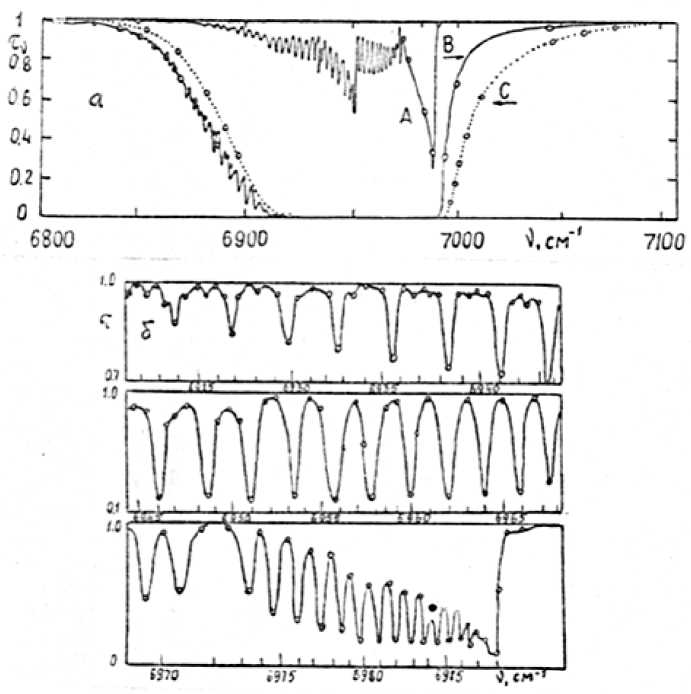
Рис. 4. Сравнение измеренных (—) и вычисленных МЧИ (о о о) спектров поглощения в полосе 1,4 мкм СО₂. а ) эксперимент [151], б ) эксперимент авторов

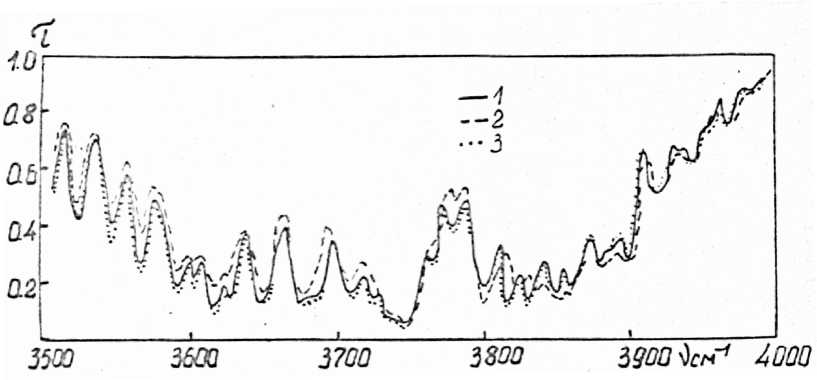
Рис. 5. Сравнение измеренного (1) и вычисленных спектров поглощения МЧИ (2)

и по эмпирической методике (3) [147]. ω_Н2 О = 0,01 г.см , Р_N2 = 1 атм