Двухпороговый знаковый дискриминатор со счетчиками - измеритель слабого постоянного сигнала в сильных шумах

В работе [1] была показана возможность точного измерения слабого стационарного сигнала на фоне сильного аддитивного шума с помощью однопороговой схемы с накоплением. Слабый постоянный сигнал интерпретировался как математическое ожидание стационарного случайного процесса. Измерение этого математического ожидания осуществлялось путем накопления в реверсивном счетчике знака выборок через шаг квантования по времени. Показание счетчика, отнесенное к числу выборок за интервал накопления, представляет собой величину, детерминиро-ванно зависящую от искомой величины сигнала в масштабе среднеквадратичного отклонения шума.

К достоинствам метода следует отнести в первую очередь простоту технической реализации схемы измерения слабого сигнала на фоне сильного стационарного шума и возможность использования "клиппирования" суммы сигнала с шумом, что в свою очередь существенно снижает требования к масштабным усилителям, устанавливаемым между источником сигнала и схемой его измерения.

Недостатком схемы можно считать необходимость априорного знания величины среднеквадратичного отклонения (или дисперсии) шума или организации специальных средств для его измерения.

В настоящей работе предлагается развитие метода [1], которое при относительно небольшом усложнении схемы позволяет получить одновременную информацию как о математическом ожидании шума (т.е. сигнале), так и о среднеквадратичном отклонении шума. Ограничения на стационарность сигнала и шума те же, что и в [1].

ДВУХПОРОГОВАЯ СХЕМА НАКОПЛЕНИЯ

Появление величины среднеквадратичного отклонения в качестве масштаба величины сигнала не случайно, поскольку в однопороговой схеме для "клиппированного" сигнала принципиально нет привязки к амплитудной шкале. Другими словами, в схеме нет масштабной "меры" сигнала.

Такую "меру" проще всего организовать путем дублирования измерений суммы сигнала с шумом по схеме из [1] для двух различных порогов, относительно которых определяется знак суммы (сигнал + шум). Именно величина расстояния между этими порогами и дает масштабную привязку к амплитудной шкале. На рис. 1 приведена схема, реализующая эту идею.

Входной сигнал, представляющий собой сумму u=s+n ( t ) постоянного сигнала s и изменяющегося

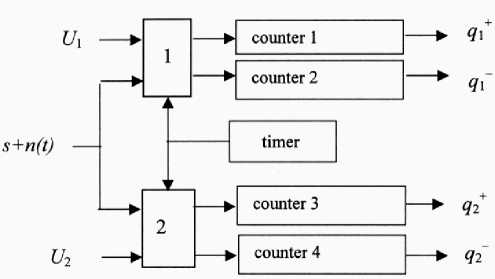
Рис. 1. Схема двухпорогового измерителя с накоплением во времени шума n(t), подается на входы двух схем определения знака. Знак суммы s+n(t)+Ui будет зависеть от уровня порога, на который настроена схема определения знака, т. е. от величины смещения Ui. Опрос текущих знаков осуществляется от единого таймера.

На выходах четырех счетчиков при нормировке их показаний к числу выборок N фактически получаются значения квантилей порядка 0.5 [2] для двух идентичных сигналов, но с разными смещениями: q 1⁺ , q 1^– , q 2⁺ и q 2^– .

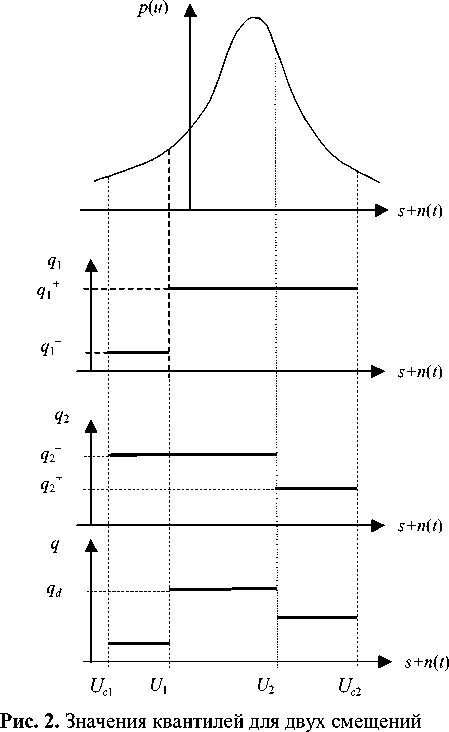
На рис. 2 показано, как величины квантилей q i соотносятся с функцией распределения шума p ( u ).

Как видно из рис. 2, квантили q1+ и q1– определяются для смещения U1, а квантили q2+ и q2– — для U2 и представляют собой четыре испытания одного сигнала с шумом. При этом, очевидно, справедливы соотношения q i++ q - = q + + q - = L (1)

которые уменьшают число независимых измерений до двух. Именно два независимых измерения и позволяют получить два параметра суммы сигнала с шумом: оценки математического ожидания

в масштабе среднеквадратичного отклонения (как и в случае однопороговой схемы [1]) и оценки дисперсии, позволяющей определить истинную величину сигнала.

Действительно, согласно [1] имеем:

q + - q - = ^фК ^ о ⁺ U i)/ ° о ^] , ⁽²⁾

q + - q 2 = ^{ф [(} ^ о ⁺ U 2 У ° о ^] , (3) где Ф ( ) — интеграл вероятностей для случая гауссового шума, s 0 — искомый сигнал и ° ₀ — среднеквадратичное отклонение шума.

Зная величины q i , по соотношениям (2) и (3), можно определить оценки s ₀ , а также при необходимости ° ₀ .

Интересно отметить, что приведенная на рис. 1 схема может интерпретироваться как трехуровневый АЦП. Из рис. 2 видно, что функция распределения шума (a) по информации о квантилях q_i , (b) и (с), аппроксимируется гистограммой (d), сформированной по трем бинам, определяемым величинами U i и реальными границами "клиппирования" сигнала с шумом u_ci .

Здесь величина q d определяется из следующих соотношений:

q d = q + ^- q - = q 2 - q - . ⁽⁴⁾

Нелишне заметить, что соотношение (4), как и соотношения (1), могут являться контрольными для фиксации сбоев счетчиков.

ВЫВОДЫ

• 1)    Относительно небольшое усложнение схемы, приведенной в [1], позволяет оценить первый и второй моменты стационарного нецентрированно-го шума. Это эквивалентно измерению медленно меняющегося слабого сигнала в присутствии сильного стационарного аддитивного шума.

• 2)    Соотношения (2) и (3) с интегралом вероятностей Ф ( ) справедливы для обширного класса реальных широкополосных шумов, которые могут быть представлены гауссовым распределением. Ф ( ) может быть задано либо таблично, либо подходящей аппроксимацией. Реальный алгоритм вычисления s 0 по значениям измеренных q i определяется видом Ф ( ), требованиями к точности измерения и конкретными свойствами встроенного в прибор микропроцессора.

• 3)    Следуя логике построения предложенной схемы измерения слабых сигналов, изложенный метод будет справедлив и для шумов негауссового типа, но в этих случаях вид функции Ф ( ) в соотношениях (2) и (3) будет иным.

• 4)    Предложенный метод комплементарен развиваемому Бенджамином Кедемом [3] методу частотного анализа сигналов на основе статистики нулей временных функций и может быть использован для оценки математического ожидания реальных сигналов с целью последующего их центрирования.