Двухступенчатая сеть Хэмминга

Несколько десятилетий назад было положено начало исследованиям методов обработки информации, называемых сегодня нейросетевыми. Сегодня исследования в области искусственных нейронных сетей (ИНС) обрели заметную динамику.

Вместе с тем реальные результаты практического применения нейросетевых технологий, особенно у нас, пока немногочисленны. Отчасти это объясняется следующими причинами: использование аппарата ИНС имеет свои особенности, которые не свойственны традиционным методам; путь от теории нейронных сетей к их практическому использованию требует соответствующей адаптации методологий, отработанных первоначально на модельных задачах; вычислительная техника с традиционной архитектурой не лучшим образом приспособлена для реализации нейросетевых методов.

Классическая сеть Хэмминга

В распознавании образов заметные успехи у сетей Хэмминга [1; 3]. Сеть Хэмминга – это одна из наиболее многообещающих распознающих, и классифицирующих нейронных сетей. В этой сети черно-белые изображения представляются в виде m -мерных биполярных векторов. Свое название она получила от расстояния Хэмминга, которое используется в сети в мере сходства R изображений входного и эталонных, хранимых с помощью весов связей сети. Мера сходства определяется соотношением

R = m - R x ,              (1)

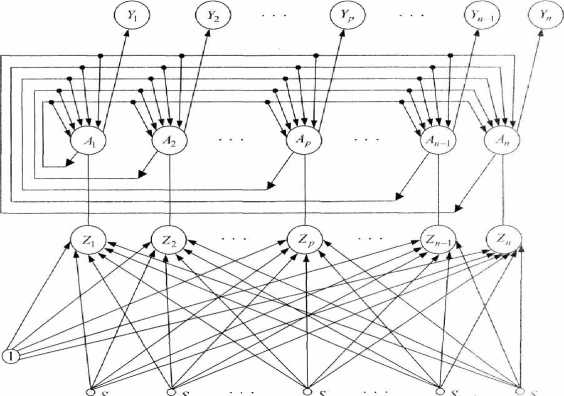
Рис. 1. Классическая сеть Хэмминга

где m – число компонент входного и эталонных R x – расстояние Хэмминга между векторами.

Расстоянием Хэмминга между двумя двоичными векторами называется число компонент, в которых векторы различны.

В силу определения расстояния Хэммин мера сходства изображений (1) может быть зад на и как число а компонент двоичных векторов, в которых они совпадают: R = a .

Запишем для биполярных векторов

S = (s_lv..,s_m) и Z = ( Z1,...,zm ) их скалярное произведение через число совпадающих и отли чающихся компонент:

m

SZ = ^ siz i = a - d ,         (2)

i =1

где а – число одинаковых компонент векторов; d – число различных компонент векторов S и Z. Поскольку т - размерность векторов, то m = a + d , следовательно, скалярное произведение (2) можно записать в виде SZ = 2 a — m. Отсюда несложно получить:

m SZ m

a —-- 1--—--и

m

∑ ^s i ^z i .

2 i=1

Правую часть выражения (3) можно рассматривать как входной сигнал нейрона, имеющего т синапс ов с весовыми коэффициентами z i /2 ( i = 1, m ) и смещением m /2 . Синапсы нейрона воспринимают т компонент входною вектора S = (s 1 ,..., s m ) . Такая интерпретация правой части (3) приводит к архитектуре нейронной подсети, изображенной в нижней части рис.1.

Одни авторы сеть, изображенную на рис.1, называют сетью Хэмминга, другие сетью Хэмминга называют только ее нижнюю часть, считая,что приведенная сеть состоит из двух подсетей – Хэмминга и Maxnet.

Сеть Хэмминга имеет т входных нейронов S 1 ,..., S _m , воспринимающих биполярные компоненты s 1 ,..., sm входного изображения. Выходные сигналы S-элементов повторяет его входной сигнал:

w lk = v k /²,-, w mk = v m /² .       (5)

Функции активации Z-элементов описываются соотношением:

0, если Uex < 0, вх.

gz (U_ex ) = 1 kU v, если 0 <  U_6X <  U_n , (6)

вх .                   вх .                             вх .          n

Un, если Uвх. > Un k1 , U n – константы.

При предъявлении входного изображения S = (s1,..., sm ) каждый Z-нейрон рассчитывает свой входной сигнал в соответствии с выраже-m нием вида (3): U   = m/2 + V w S* и с помо- вХ . ^Zk                               ik i i=1

щью функций активации определяет выходной сигнал U. Выходные сигналы U V.,..,U v вх.Zk                                       вых. Z1        вых. Zn

Z-элементов являются входными сигналами a 1 ,..., a _n верхней подсети, которой является подсеть Maxnet.

В подсети Maxnet в результате онного процесса выделяется один и нов A1,..., An, имеющий наибольший сигнал ap (p е {1, 2,..., n}), то есть нейрон Ap становится «победителем», а это указывает на то, что предъявленное изображение

*          *          *

S = ( s ! ... s m ) ^на^-

иболее близко, в смысле заданной меры близости к эталонному изображению Vp = (vp ... vpm ) .

Существенное достоинство сети Хэмминга заключается в том, что она не требует трудоемких вычислительных процедур для своего обуче- ния. Заметный недостаток сети: она не выделяет два и более эталонных изображений, имеющих с предъявленным одинаковые максимальные меры близости [1; 3].

Использование двухступенчат Хэмминга в процессе распозн

Набазеклассическоймоделираспознавания,кото рая не может считаться идеальной,необходимо пост роить гибрид моделей с более лучшими результатами распознавания,чем классическая модель [2; 4].

На основе данной теории была поставлена задача построить нейронную сеть Хэмминга, которая будет распознавать зашумленные буквы кириллицы.

На вход сети поступает изображение a*b клеток, содержащих сигнал 1 (черная клетка) либо 0 (белая клетка). Наличие a*b черно-белых элементов в изображении определяют a*b S-нейронов, воспринимающих элементы входных изображений. Число Z-, a- и Y-нейронов определяем по числу эталонных изображений. Зная векторы эталонных изображений и их число по соотношению (5) рассчитываем матрицу весов связей й подсети сети Хэмминга. Далее расс смещения Z-неиронов: bi = m/2, где i-l,m, (m – число воспринимающих элеме кции активации Z-нейронов задади нием         k1 = ... (задается пользователем в программе), Un = 1/k1 . Далее предъявляем сети по очереди зашумленные образы, и сеть выдает число эталонных образов, имеющих с предъявленным наибольшую степень сходства. Если это число равно 1, то сеть заканчивает свою работу, иначе продолжает поэлементное сравнение. поэлементном сравнении участвуют только те эталонные образы, которые имели степень сходства выше установленного нами порога с предъявленным образом на предыдущем этапе.

Предлагается исследовать части тех изображений, которые имеют наибольшую степень сходства с предъявленным образом. Части изоб- делитель a, b1 – делитель b, число их a^-) будут обрабатываться a1b1

аналогично целому изображению, то есть схема распознавания выглядит следующим образом.

• 1.    Изображение a*b поступает на вход первой сети Хэмминга.

• 2.    Определяется число нейронов (эталонных образов), имеющих степень сходства с предъявленным образом выше установленного нами порога, получаем число J.

• 3.    Если J = 1, то изображение считается распознанным.

• 4.    Если J > 2, то каждый из образов-эталонов, соответствующих нейронам, разбивается на час-

• ab

нейронных сетей анало- ^a 1 ^b 1

гичных первоначальной.

^a коэффициен- a ₁ b ₁

тов схожести, расчтитываем средний из них, с помощью сети Maxnet выбираем максимальный из этих коэффициентов и делаем заключение о том, какой из эталонных образов наиболее схож с предъявленным.

Результаты эксперимента

Была поставлена задача проэмулировать работу данного метода. В базу эталонов были введены 33 заглавные буквы русского алфавита, размером 15*15 клеток.

На первом этапе сети поочередно были предъявлены эти же образы. В результате все они были безошибочно распознаны, но при условии, что gZ (Uвх.) - 1. Здесь же была замечена следующая закономерность: кр = ткх k р - коэффициент распознавания gz (U^ ) из формулы (6), к1 - коэффициент пропорциональности из той же (6) формулы, m = a*b – размер изображений букв (число клеток). Таким образом, мы получаем условие ki ^-,                 (7)

m при котором в (7) можно получить и наглядную интерпретацию числа кр, это будет не просто число, по которому определяют схожесть с эталоном, оно будет показывать процент «похожести» предъявленного образа на эталон. При невыполнении (7) мы не можем выделить образ, максимально похожий на предъявленный.

На втором этапе сети Хэмминга был предъявлен образ, показанный на рис. 2.

												0
				0		0
0					0					0	0
0			0				0		0	0	0
0								0	0	0
0							0	0		0	0
0						0	0			0	0
0					0	0				0	0
0					0						0
0			0	0						0	0
0		0	0					0		0	0
0	0	0								0	0
0	0				0					0	0
0										0	0

Рис. 2. Зашумленный образ буквы «Й»

Витоге сетьсделала следующийвывод:предъ-явленный образ на 95% похож на образ буквы «Й», на 94,1% – на букву «И», которые в эталонных вариантах выглядят, как показано на рис. 3.

																					0	0	n
	0	0										0	0			0	0					0					0	0
	n	0									0 0		n			0	0									0	0	0
	0	0								0	0 0		n			0	0								0	0	0 0 0 0
	0	0							0 0		0		n			n	0						0 0
	0	0						0	0		0		0			0	0						0 0				0 0
	n	n					0	0				n	0			n	0					0	0				0 0
	0	0				0	0					0	0			0	0				0	0					0 0
	0	0				0						0	0			0	0			0	0						0	0
	0	0		0	0							0	0			0	0		0	0							0	0
	n	0	0	0								0	0			0	0	0	0								0	0
	0	n	n									0	n		0 0			0									n	0
	0	0										0	0		0 0												0	0

Рис. №3. Эталонные образы букв «И» и «Й»

Далее сети был специально предъявлен образ, не имеющий ничего общего ни с одним из эталонных образов (см. рис. 4).

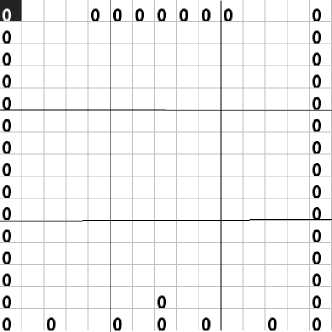
Рис. 4. Предъявленный образ

Результат довольно интересный: предъявленный образ на 61,7% похож на образ буквы «Г»

(см. рис. 5), что не соответствует действительности.

Рис. 5. Эталонный образ буквы «Г»

На основе этого предложено поставить порог распознавания 80-85%, то есть не рассматривать те эталонные образы, которые не перешагнули данный порог.

ab

части a1b1

предъявленного образа сравниваются с соответствующими частями тех образов эталонов, которые перешагнули порог распознавания. Процесс распознавания по частям ведется по формулам (4)-(6) с условием (7). На выходе мы получим J ab чисел. Сложив компоненты этих a1b1

наборов, получаем J чисел, которые подаются на сеть Maxnet и дают на ее выходе конечный единственный результат.

Выводы

Предложенный метод позволяет обойти главный недостаток сети Хэмминга: она не выделяет два и более эталонных изображений, имеющих с предъявленным одинаковые максимальные меры близости. За счет появления порога распознавания мы выделяем несколько эталонных изображений, имеющих коэффициент сходства с предъявленным изображением выше заданного порога. Согласно неравенству (7) мы выбираем коэф         k1 в формуле (6), также при превращении неравенства (7) в равенство мы видим наглядную интерпретацию коэффициента рас            kр, который становится процентом «похожести» предъявленного изображения на эталонный образ.