Двухуровневая оптимизация параметров стана пилигримовой прокатки труб
Автор: Лехов О.С., Раскатов Е.Ю.
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Общие проблемы машиностроения
Статья в выпуске: 1-3 т.13, 2011 года.
Бесплатный доступ
Описан алгоритм двухуровневой оптимизации параметров стана пилигримовой прокатки труб. Приведены результаты оптимизации технологических параметров процесса прокатки и параметров линии привода пилигримового стана.
Оптимизация, алгоритм, энергоёмкость, математическая модель, целевая функция, динамический момент
Короткий адрес: https://sciup.org/148199677
IDR: 148199677 | УДК: 621.771.06-589.4
Текст научной статьи Двухуровневая оптимизация параметров стана пилигримовой прокатки труб
в валки может преждевременно выйти из строя вследствие высоких динамических нагрузок, а интенсивные крутильные колебания элементов главной линии и вибрации валковой системы и рабочей клети могут привести к ухудшению качества труб.
Для определения оптимальных параметров пилигримового стана использован алгоритм двухуровневой оптимизации [1], который включает решение следующих задач:
-
1) оптимизация параметров технологического процесса при заданном сортаменте труб (верхний уровень оптимизации);
-
2) оптимизация параметров линии привода стана при заданных параметрах технологического процесса и электродвигателя, определенных на верхнем уровне оптимизации.
Наиболее важным вопросом является выбор критериев оптимизации, однако задача оптимизации усложняется тем, что пилигри-мовый стан оценивается по многим и в ряде случаев противоречивым критериям, таким как производительность (П), энергоёмкость (Э), динамическая нагруженность (Н), качество проката (К). Учитывая актуальность экономии материально-энергетических ресурсов в качестве целевой функции при решении задач оптимизации параметров пилигримового стана на верхнем уровне целесообразно принять энергоёмкость технологического процесса (Э), а на другие показатели наложить ограничения. Таким образом, задача оптимизации технологических параметров (верхний уровень) может быть сформулирована след у ющи м образом:
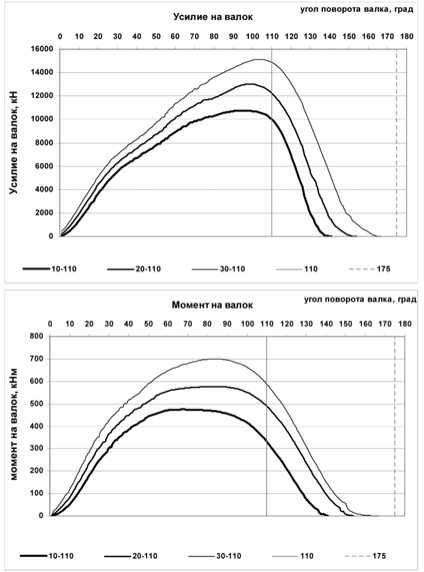
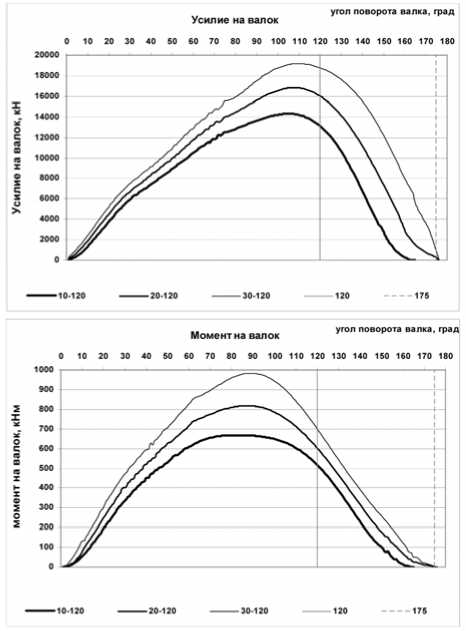
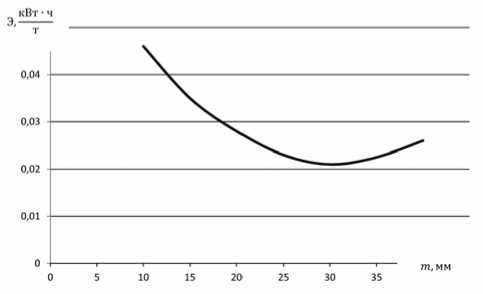
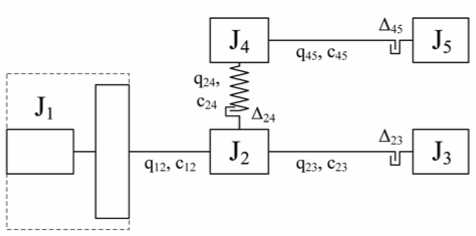
Минимизировать Э( Х). Х = [m, to] при ограничениях: П>Пзад; m(1) Математическая модель процесса пилиг-римовой прокатки включает известные зависимости для расчета силовых параметров, удельного расхода энергии и производительности. Сопротивление пластической деформации определяется по зависимости [2]: σs = 288 U0,107 (lnε)1,45 e^0,00235T; где σs – сопротивление пластической деформации, МПа; U – скорость деформации, 1/с; ε – степень деформации, %. Графики изменения усилий и моментов прокатки приведены на рис. 1-3. Рис. 1. Изменение усилий и моментов на валок. Калибровка 105-70-45-140 Удельный расход энергии Эуд = 2 М ω tM/G (2) где M – момент прокатки на один валок, кН·м; ω – угловая скорость валка, 1/с; tM – машинное время прокатки гильзы, с. _ L2 60(0Б +0П ) tM = ~ m n 2п где Lг – длина гильзы, мм; n – угловая скорость валка, об/мин;ΘБ, ΘП – соответственно центральные углы бойковой и полирующей частей валка; G – масса гильзы, т. Рис. 2. Изменение усилий и моментов на валок. Калибровка 110-65-45-140 Для расчета использованы следующие значения параметров:G=3200 кг, n=45 об/мин, Т = 10500С, диаметр гильзы 500 мм, диаметр дорна 300 мм, диаметр трубы 325 мм, допустимое усилие прокатки [P]=8000 кН, ΘБ=1100, ΘП=650. Для решения задачи оптимизации параметров пилигримового стана использован комбинированный алгоритм, построенный на базе методов случайного поиска и симплекса Нелдера-Мида [1]. В качестве целевой функции на верхнем уровне оптимизации использована удельная энергоёмкость процесса пилиг-римовой прокатки. Диапазоны изменения варьируемых параметров: 10≤m≤35 мм, 3,14≤ω≤6,28 1/с. Результаты расчета приведены на рис. 4. Полученные результаты с учетом данных теоретического исследования напряженно-деформированного состояния металла в очаге деформации пилигримовой прокатки [3] позволяют обоснованно выбрать оптимальную величину подачи гильзы в валки с позиции выполнения заданной производительности, снижения энергоёмкости технологического процесса и нагруженности механического оборудования и улучшения качества бесшовных труб. С учетом результатов комплексного исследования оптимальная величина подачи равна 20 мм. Рис. 3. Изменение усилий и моментов на валок. Калибровка 120-55-45-140 Рис. 4. Зависимость удельной энергоемкости от величины подачи гильзы в валки пилигримового стана Как отмечалось выше, при интенсификации режимов пилигримовой прокатки возрастает как уровень динамической нагруженности несущих элементов главной линии пилигримо-вого стана, так и взаимная связь процессов, происходящих в очаге деформации и линии привода [3]. Таким образом, динамические параметры привода, схема компоновки привода и конструктивные параметры, параметры очага деформации в совокупности определяют динамическую нагруженность элементов стана, в частности зубчатых передач, и качество труб. Кроме того, в машинах и агрегатах периодического действия наблюдается большое количество поломок несущих элементов привода, основной причиной которых являются динамические нагрузки [1]. В связи с этим в качестве критерия оптимизации (второй уровень) параметров пилигримового стана целесообразно использовать динамическую нагруженность, поскольку снижение данного показателя позволит повысить долговечность несущих звеньев, а также улучшить качество труб. Таким образом, в качестве целевой функции целесообразно принять максимальную амплитуду динамического момента, то есть F = MД где MД - максимальная амплитуда момента крутильных колебаний, кН^м. Однако линия привода пилигримового стана включает в свой состав шестеренную клеть, на моторном валу имеется маховик, то есть является многомассовой системой. В связи с этим в процессе оптимизации необходимо добиться снижения динамических нагрузок во всех или более слабых звеньях линии привода, то есть задача является многокритериальной. Поэтому целевую функцию (F) следует записать в виде [1], а задачу оптимизации (второй уровень) сформулировать следующим образом: Минимизировать f=X м+X ’-1 Kj (Mj - мД) X=[ c, J ] при параметрических ограничениях: cW<c<c,(2); Ji«J Решение задачи оптимизации параметров линии привода пилигримового стана осуществляется с помощью математической модели, включающей модели очага деформации и линии привода. Система дифференциальных уравнений, описывающих динамические процессы в линии привода пилигримового стана согласно расчетной схемы (рис. 5), имеет вид: J 1^1 = M Дв-с 12 (Ф1 -Ф2 )-912 ((Р1- Ф2 ) J 2ф 2 = C12 (ф 1 - Ф 2 )+q 12 (ф1 - ф2 )-C 24 (ф 2 - Ф4 )--q 24 (ф2 - ф4 )- C 23 (Ф 2 -Ф 3 )-923 (ф2 - ф3 ) J3ф3 C23 (ф2 Ф3 )+q23 (ф2 ф3 ) M3’ J4ф4 = C24 (Ф2 -Ф4 ) +924 (ф2 - ф4 ) - C45 (Ф4 -Ф5 ) - -q 45 (ф4- ф5); J5ф5 = C45 (Ф4 -Ф5 ) +q45 (ф4 - ф5 ) - M5’ Тэ M дв = - M Дв (<&lZ^ol &ю0 где Tэ – электромагнитная постоянная двигателя; ϑ – модуль жесткости механической характеристики; ω0 – угловая скорость на холостом ходу, 1/с; J – момент инерции сосредоточенной массы, т·м2 (кН·м·с2); c – жесткость упругой связи, кН·м/рад; q – коэффициент эквивалентного вязкого демпфирования, кН·м·с; M3, M5 – моменты на валках, кН·м; ϕ,ϕ& ,ϕ&& – соответственно угол поворота, угловая скорость и угловое ускорение сосредоточенной массы; K3, K5 – эмпирические коэффициенты, определяющие время переходного процесса захвата гильз валками. Рис. 5. Расчетная схема линии привода пилигримового стана Задача оптимизации решена для наиболее тяжелого режима нагружения линии привода пилигримового стана – мгновенного приложения нагрузки при захвате гильзы валками. Время переходного процесса захвата гильзы валками 0,05 с. В качестве варьируемых параметров использованы жесткости упругих связей с23, с45. Начальные значения конструктивных параметров равны параметрам пилиг-римового стана №2 ОАО «ЧТПЗ», диаметры шпинделей которого 390 мм. Решение системы дифференциальных уравнений (4) проводили методом Рунге-Кутта. Выводы: в процессе оптимизации варьировали жесткости шпинделей (с23, с45) в диапазоне 7000-14000 кН·м/рад. Установлено, что при мгновенном приложении нагрузки (0,03÷0,05 с) при захвате гильзы валками пи-лигримового стана жесткости шпинделей практически не влияют на максимальную амплитуду динамического момента крутильных колебаний, которая равна 1130÷1170 кН·м. Эти динамические нагрузки следует учитывать при расчете элементов линии привода пилигримовых станов на прочность и долговечность.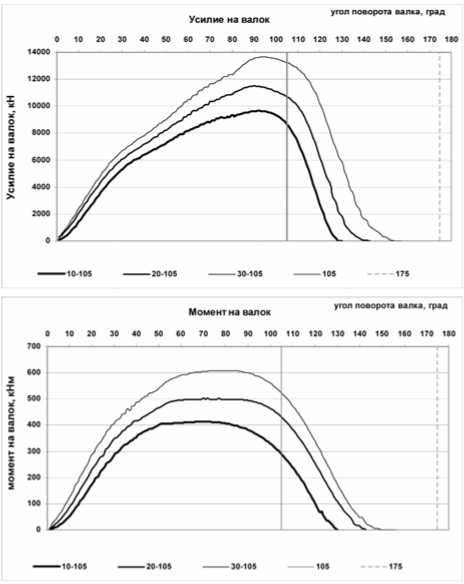
Список литературы Двухуровневая оптимизация параметров стана пилигримовой прокатки труб
- Лехов, О.С. Оптимизация машин для деформации непрерывнолитых заготовок. -М: УИФ «Наука». 1995. 182 с.
- Мазур, В.Л. Сопротивление деформации низколегированных сталей/В.Л. Мазур, Д.Д. Хижняк//Сталь. 1991. №8. С. 41-43.
- Чучулин, Ю.Б. Измерение нагрузок на шпинделях валков пильгерстана/Ю.Б. Чечулин и др.//Металлург. 2007. №6. С.47-49.


