Двумерная модель течения материала в канале шнека с неподвижной крышкой

Разработка современных технологий в пищевой промышленности базируется на использовании высокоинтенсивных воздействий на микроуровне. При этом анализ факторов производственного процессавыявляет наиболее эффективные технологические приемы, использование которых позволяет обосновать эффективное совершенствование процессов извлечения ценных компонентов. Развитие технологических инноваций в пищевой промышленности основано на моделировании процессов гидродинамики в рабочей зоне установок при значительных изменениях внешних воздействий. Габариты питающего витка шнекового пресса оказывают существенное влияние на его расходно-напорные характеристики. Методы математического моделирования потоков учитывают эти характеристики. Выбор параметров модели в равновесных условиях оказывают существенное влияние на последующую оптимизацию технологии. Перспективным направлением в этом случае являются модели переноса, определяемые гидродинамикой фазового перехода.В работе анализируется влияние габаритов на режим течения вязко-пластичного материала [1–14].

Основная часть

Материал, находящийся в канале вращающегося шнека и ограниченный неподвижным корпусом, начнет двигаться поступательно по каналу вследствие возникающей в нем деформации сдвига – появляется вынужденный (прямой) поток. Основными параметрами, определяющими величину объемного расхода, являются глубина, и ширина канала, диаметр шнека и частота его вращения. Необходимым условием существования этого потока является сохранение в материале напряжений сдвига, что возможно только в том случае, если материал имеет определенную вязкость. Условием возникновения обратного потока является избыточное давление, создаваемое сопротивлением головки. Представим себе в этих условиях, что шнек не движется. Тогда под действием давления со стороны головки материал потечет от нее вдоль шнекового канала –в обратном направлении. Величина объемного расхода противотока также зависит от глубиныканала, диаметра и длинны шнека, вязкости материала и величины давления в головке. На практике, однако, в канале шнека никогда не возникает противоток, а давление в головке оказывает своеобразное ограничение прямому потоку, которое рассматривается теоретически как противоток, а производительность шнекового нагнетателя – как суммарный расход двух потоков. Для учета геометрии канала разрабатывалась математическая модель скоростного напора в прямоугольном канале.

Для описания распределения скоростей использовалась двумерная задача Пуассона с граничными условиями первого рода. Задача сводится к решению уравнения Пуассона U xx +U yy =0 внутри прямоугольника при краевых условиях:    u(0,y) =V, u(a,y) =V,   u(x,0) =0

u(x, b) =V . Будем искать вначале нетривиальные частные решения уравнения Пуассона, удовлетворяющие граничным условиям u(x,0) =0, u(x,b) =V в виде u(x,y) =X(x) •Y(y) . Подставляя это выражение в уравнение Пуассона, получим X” (x)xY(y) +X(x)-Y(y)” =0 , откуда делением на X(x) х Y(y) найдем соотношение между производными и их функциями:

X" _ Y" _ .2

X ( x )     Y ( У )                      ( 1 )

,

Левая часть равенства (2) может зависеть только от x , или быть постоянным числом, не зависящим от координат. Аналогично и правая часть не зависит от координаты у . Следовательно, эти соотношения выполняются при их равенстве постоянной величине X ² . Допуская, что Y(0) =Y(b) =0 , получим задачу Штурма-Лиувилля:

[Y" + Я2 ■ Y(у) = 0

, 0 < у < b

I Y(0) = Y(b) = 0

Для решения уравнения (2) используем операционный метод, основанный на интегральном преобразовании Лапласа, позволяющий преобразовать дифференциальное уравнение (оригинал) к её алгебраическому аналогу (изображению). В этом случае решение алгебраического уравнения будет соответствовать решению дифференциального. Используя прямое преобразование Лапласа, преобразуем уравнение (2) к виду:

Я ² ■ L ⁽ 5 ) - dy 0 - 5 ² ■ L ⁽ 5 ) - 5 ■ у 0 = 0 (3)

Разрешая полученное уравнение (3) относительно изображения искомой функции L(s) находим полученную зависимость, считая s простой переменной:

L ^{( 5} ) =

dy 0 + 5 ■ У 0

я + 5

Используя обратное преобразование

Лапласа, преобразуем уравнение (4) к виду:

Подставляя x =a в уравнени е(12) находим постоянные из следующего соотношения:

Y ( У ) =

dy 0 - sin ( X - y ) + y 0 - cos ( X - y ) - X

X

, ( n П 1       , n П 1  „ an - ch I--a I + bn• sh\--a I = 0

V b )        V b )

Используя (5) с учето м(2) получаем собственные значения и собственные функции двумерной задачи Пуассона на прямоугольнике:

n - П         • ( n П 1

^Xn = -j-, ^Yn ⁽ y ) = ^s iⁿ   .    .' I , n = ^1,2, - ^, ”            (6)

b            V b )

В тоже время при x =a в уравнени е(12) с учето м(13) имеем:

to

V = Z

. n n - n ^a n '^sinHr • y

V b

Соответствующие функции X n (x) являются решениями уравнения X” (x) -X ² X(x) =0, откуда используя прямое преобразование Лапласа, преобразуем это уравнение к виду:

s ² • L ( s ) - X ■ L ( s ) - dx 0 - s • x 0 = 0 (7)

Интегрируя ряд (14) получаем следую-

щие соотношения для a n :

an

~ b      /       \         f 0, n четное

2             П n • n 1I ’

= - - V • sinl--y I dy, a =< 4 • V b 1      I b ) n ----, n нечетное

⁰                                  I n • П

Разрешая полученное уравнени е(7) относительно изображения искомой функции L(s) находим полученную зависимость, считая s простой переменной:

Таким образом, решение задачи на прямоугольнике имеет вид:

(    \  4 • V V¹

u ^{( x} , y )=—^.

^П n = 1

, Г ( 2 • k + ] ) • ( a — sh

L          b

^x ) ^п 1 ,,_in Г ( 2 k ^{+1) n} • y '

J L         ь        _

( 2 ^ k + 1 ) • a n l

( 2 • k + 1 ) • sh ------^-----

L ⁽ s ) =

—

dx ₀ + s • x ₀ X — s²

Используя обратное преобразование Лапласа, преобразуем уравнение (4) к виду:

X ( x ) = x • ch ( X- x ) + dx 0 • sh"' )    ( 9 )

X

Полученное решение (16) соответствует краевой задаче u(0,y) =V, u(a,y) =0, u(x,0) =0 u (x,b) =0 . Проведя замену переменных в (16) после очевидных алгебраических преобразований получаем решение исходной задачи с граничными условиями u(0,y) =V, u(a,y) =V, u(x,0) =0 u (x,b) =V :

Используя (9) с учетом граничных условий получаем собственные функции двумерной задачи Пуассона на прямоугольнике по координате x :

u ( x , y ) = v — 4V-t П n = 1

Г ( 2 - У + 1 )-( 6 - у У п 1   _m Г ⁽ 2 • k ^{+ 1 )} • ⁿ ^ x ~

L          a          J L       a

(2^ + 1 ) ^ sh | > k ^{+ 1 ) bn 1}

^Xn ^{( x} ) = a n -ch I

где a n и b n - произвольные постоянные. Соответствующие функции решения уравнения Пуассона на прямоугольнике будут иметь вид:

u n ^{( x} , y ) =

В качестве решения исходной задачи

возьмем ряд:

где a, b – габариты канала (a > b), м; x, y – декартова система координат, (0 < x < a) и (0 < y < b); V – скорость движения стенок канала (1 м/сек). Задача (17) формулируется как двумерная c неподвижной крышкой и движущимися стенками. В этом случае скорость сдвига в канале при скорости его стенок V м/сек и неподвижной крышке пропорциональна градиенту, модуль которого определяет скорость сдвига в прямоугольном канале. Интегрируя модуль градиента, определяем среднюю скорость сдвига в канале:

у ( V , a , b ) =

to 4* и j: ja. kt 11 n=1 , n 2 n •:—2 • n • y+4 я- :• ch I----------------------------------- V                 a a2 •sh k — 4 я-y^kI — (^k + fbb-n L      a      J П 2-п-x + 4-n-k-x 1 cos II V        a        ) 2 - dxdy a^b

Для Ньютоновской реологии важна средняя скорость сдвига, которая в случае одномерной задачи Куэтта равна скорости сдвига на движущейся крышке канала. Это связано с линейным характером изменения скорости по высоте канала. Изменение скорости в каналеc неподвижной

крышкой и движущимися стенками носит нелинейный характер, определяемый уравнением (17). Поэтому среднее значение градиента по площади сечения прямоугольного канала Y ( V , a , b ) определяет среднюю скорость сдвига в этом канале. При изменении габаритов канала

будет меняться и средняя скорость сдвига у (V, a, b) в канале, средняя скорость сдвига, как усредненный по площади профиля модуль градиента скорости материала аппроксимируется регрессионной зависимостью полученной для скорости движущейся крышки v относительно габаритов канала шнека:

у(v, b, h ) = (v с/М)•

a0

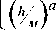
+ (bM)[a2 '(мa3 ] • {a4 + a5 • exp [a6 • (hM)]} - a7 [ • Гц

где v – скорость крышки канала; b – ширина канала; h – высота канала.

Таблица 1.

Значения коэффициентов регрессионной зависимости

Values of regression dependence coefficients

Table1.

Коэффициенты Coefficients	a 0	a 1	a 2	a 3	a 4	a 5	a 6	a 7
Значения Value	1,751	0,949	7,932	0,712	4,426	1,372	29,037	13,736

Уравнение (2) позволяет определить напряжение сдвига т ( Y по скорости сдвига материала у ( v , b , h ) . Учитывая симметричность и линейность распределения скорости в канале относительно его середины, получаем распределение скорости сдвига по высоте: у • у ( v , b , h ) • y , где y - текущая высота канала, 0 .