Двумерная модель зернограничной диффузии и окисления
Автор: Чепак-гизбрехт М.В., Князева А.Г.
Статья в выпуске: 1, 2022 года.
Бесплатный доступ
Измельчение структуры материалов сопровождается изменением физико-механических свойств. Это происходит во многом благодаря накоплению энергии и дефектов в структуре, что активизирует диффузию примесей, содержащихся в материале. Увеличение числа границ зерен и стыков может являться причиной неупругого поведения материала, его дополнительной химической активации. Для одних металлов и сплавов это приводит к упрочнению, а для других - к стремительной деградации механических свойств. Зернограничная диффузия в таких материалах является основным механизмом транспортировки легирующих компонентов или вредных примесей, поэтому ее исследование важно. В настоящей работе представлена двумерная модель зернограничной диффузии в материале с явным заданием структуры. В модели учитывается наличие химических превращений, которые могут определять механизмы коррозии в условиях эксплуатации. Структура материала для простоты расчета принята симметричной и содержит две фазы: зёрна и граничную фазу. Диффузионные и кинетические параметры фаз могут отличаться. Модель представлена в безразмерном виде так, что расстояния между соседними зернами или ширина граничной фазы одинаковы, а размеры зерен могут изменяться. В зависимости от соотношения размеров фаз можем говорить о микро- и нанокристаллической структуре. Задача решена численно с использованием неявной разностной схемы и расщепления по координатам. Для расчетов приняты диффузионные и кинетические параметры, которые близки к параметрам зернограничной диффузии кислорода в титане и окислению титана соответственно. Интегральные концентрации отражают динамику (кинетику) накопления кислорода и оксидов по площади расчетной области. Представлены результаты, показывающие роль изменения констант реакций в фазах и соотношения размеров зерен. Модель может быть полезна для оценки степени влияния зернограничной диффузии на процесс окисления и сопутствующего изменения свойств, а также для постановки соответствующих экспериментов.
Диффузия, оксиды титана, границы зерен, тройной стык, моделирование
Короткий адрес: https://sciup.org/146282433
IDR: 146282433 | УДК: 538.931,
Текст научной статьи Двумерная модель зернограничной диффузии и окисления
ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2022PNRPU MECHANICS BULLETIN
В последнее время активно исследуют способы упрочнения материалов за счет измельчения структуры при внешнем нагружении. Для некоторых материалов измельчение размеров зерен и зернограничная диффузия примесей из атмосферы приводят к повышению механических характеристик, для других материалов измельчение зеренной структуры способствует повышению хрупкости [1]. Например, внутреннее окисление ванадиевых сплавов с содержанием циркония повышает их термическую стабильность и механические свойства [2]. В области температур, близких к комнатной, существенно усиливается влияние границ зерен на процесс пластической деформации: наблюдаются локализации пластического течения сплава вблизи границ зерен с образованием микротрещин. Механизмы неупругого и сверхпластичного поведения материалов различны. Одним из них является зернограничная диффузия [3]. При определенных температурах она приводит к сглаживанию границ и повышению энергии активации отдельных зерен. Дефекты и структура зерен изменяются в процессе термомеханической обработки. Разница в энергии, запасенной в соседних зернах, приводит к движению их границ [4].
При измельчении структуры возможно повышение прочности при сохранении пластичности для материалов из титана. При этом возрастает количество дефектов и доля границ зерен. В исследовании [5] показано, что субмикрокристаллический титан, полученный методом пластической деформации, окисляется в диффузионном режиме в интервале температур 873–1073 К. В других интервалах температур скорость роста оксидного слоя может быть описана зависимостями разного вида [6–9]. Отмечается, что парциальное давление кислорода не влияет на соотношение оксидов в окисленном слое, однако приводит к изменению размеров зерен оксидов. Авторы [10] отмечают, что измельчение размеров зерен в структуре (изучались образцы с размерами зерен 460 и 150 нм) приводит к ускорению процесса окисления титанового сплава. Повышение температуры способствует интенсификации роста оксидных фаз, количество теплоты, выделяющееся и поглощающееся в ходе окисления, меняется и имеет максимумы и минимумы в разных интервалах температур, что может быть обусловлено полиморфными превращениями. В другом исследовании показано, что в процессе высокотемпературного окисления титановых преформ на границе с рутилом образуется слой окисла. Этот слой имеет толщину в несколько сотен микрон и размер зерен внутри этого слоя составляет от 200 до 300 нм вблизи титана [11]. Авторы отмечают, что в зависимости от температуры и времени выдержки реализуются такие условия смещения зоны реакции за счет диффузии, что окисленный слой может как плотно прилегать к металлу, так и отслаиваться от него (при более высоких температурах и долгой выдержке).
Таким образом, в условиях эксплуатации наноструктурирование может иметь как положительные, так и отрицательные последствия, например деградация структуры вследствие окисления и коррозии. Для того чтобы понять механизм окисления, необходимо привлекать математическое моделирование.
В настоящее время существует несколько теорий, позволяющих описать количественные и качественные характеристики насыщения поверхности примесями из агрессивной окружающей среды и накопление повреждений. Большая часть таких моделей – феноменологические. Они позволяют с помощью простых экспериментов на образцах оценить работоспособность конструкций из аналогичного материала в условиях работы в агрессивных средах. Например, согласно государственным отраслевым стандартам, для определения работоспособности конструкций из металлических сплавов измеряют толщину оксидной пленки, которая образуется за некоторое время. Законы роста этой пленки могут быть различными. Самые простые физико-химические и математические модели описывают изменение скорости роста коррозионной пленки и по-врежденности с учетом некоторых внешних параметров. Значения параметров, входящих в такие модели, находятся в ходе обработки экспериментальных данных. Например, в работе [12] содержатся математические модели, в которых учитывается зависимость скорости коррозии тонкостенной оболочки от уровня напряжений. В исследовании [13] описывается влияние толщины окисляющейся пластины на длительную прочность при внешней нагрузке.
Более сложные модели учитывают диффузионный механизм проникновения окислителя в материал [14] и динамику коррозионного фронта. Так, даже с помощью приближенного решения уравнения диффузии для проникания агрессивной среды в материале [15] удается найти достаточно точный критерий оценки сохранения длительной прочности в процессе ползучести. Например, в [16] описан запирающий эффект, когда плотный слой проникших в материал элементов существенно тормозит дальнейший перенос окислителя диффузией.
Многомасштабные или многоуровневые модели основаны на законах термодинамики и исследуют процесс коррозии в деталях. В таких моделях могут учитываться: особенности подвода окислителя из окружающей воздушной или жидкой среды; наличие химических реакций на поверхности или в глубине материала; взаимосвязь между параметрами окисленного слоя и внешними нагрузками; геометрические особенности расположения деталей относительно окислителя; электрохимические или физические взаимодействия агрессивной среды и конструкции на уровне атомов и молекул. Так, в исследованиях [17; 18] предлагаются модели, претендующие на описание кинетики химических реакций в деформируемых средах. Учитываются не только внешние нагрузки, но и возникновение внутренних напряжений вследствие химических превращений. Однако соб- ственно диффузия описывается в рамках классических законов. Проблемы когезии окисленного слоя при внешнем нагружении обсуждаются в работе [19]. Авторами предложена модель для описания межкристаллитного коррозионного растрескивания, которая включает уравнение Фика для диффузии и уравнение анодного скольжения – растворения. Зона адгезии описывается отдельно с использованием параметра деградации. Показано, что более высокая скорость роста трещины в условиях холодной обработки является результатом совместного действия разрушения и окисления. В работе [20] анализируется модель эволюции искривленных границ раздела и поверхностей пустот, пересеченных границами зерен, в тонкопленочных металлических соединениях, имеющих структуру бамбука, в результате совместного действия капиллярных сил и явления электромиграции. В обзоре [21] подробно рассмотрены подходы к многоуровневому моделированию коррозии в атмосфере. Например, комплекс взаимосвязанных моделей GILDES предполагает детальное описание процесса для каждой из областей, в которой он происходит: газ – поверхность – жидкость – осаждение – электрод – твердое тело. Так, в газовой фазе описывается процесс транспорта химически активного реагента из источника к поверхности. Применительно к поверхности в модели рассматриваются условия осаждения (или испарение) реагента в рамках закона Генри. Если коррозия происходит в жидкой среде, то помимо условий переноса учитывают влияние толщины раствора и концентрации реагента в нем. Модель осаждения описывает процесс образования металл-анионных комплексов и интерме-таллидов, транспорт ионов внутри поверхности твердых тел. Проводимость среды оказывает заметное влияние на скорость осаждения или коррозии, поэтому отдельно рассматривается динамика плотности тока. В модели твердого тела рассматривается поведение металла в кислой среде в динамике. В основе многозонной модели переноса и реакции (MITReM) [22; 23] лежат уравнение Пуассона и уравнения баланса массы для всех компонентов электролита, а также уравнение баланса заряда. Эта модель позволяет анализировать атмосферную коррозию, гальванические процессы осаждения или коррозии, питтинг-коррозию и преципитацию. В случае, когда невозможно оценить доминирующий механизм или фактор, приводящий к коррозии (агрессивная среда, наличие тока, наличие промежуточных неравновесных фаз и т.д.), полезными могут быть модели, основанные на методе клеточных автоматов, которая учитывает вероятностный характер каждого из протекающих процессов [24].
Однако зеренная структура материалов в перечисленных работах не анализируется, хотя именно зернограничная диффузия во многом определяет прочностные свойства и химическую активность материалов с микро- и наноструктурой [25; 26]. Поэтому ее исследованием заинтересовались еще в прошлом веке. Первые модели зернограничной диффузии были сформулированы таким образом, чтобы было удобно найти прибли- женные аналитические решения [27]. Более поздние работы учитывали соотношения скоростей диффузии в границе зерна и зерне, расстояние между этими границами и характерное время, в течение которого реализуются режимы диффузии (А, В, С и их сочетания) вдоль границ [28]. Эти модели еще называют моделями изолированной границы, поскольку в их основе лежит предположение, что граница имеет бесконечно малую толщину в сравнении с зернами, соседние границы параллельны друг другу и между ними отсутствует диффузионное взаимодействие. Поверхность является постоянным источником диффузанта, а сами границы являются путями ускоренной диффузии. Моделей зернограничной диффузии, основанных на данных предположениях и отличающихся разными тонкими эффектами, в литературе достаточно много. В разных работах учитываются такие факторы, как: зависимость коэффициента диффузии от температуры или наличия дефектов в структуре [29; 30], наличия примесей на границах [31]; наличие некоторой промежуточной зоны (или даже несколько слоев в такой зоне), где скорость диффузии является средней между скоростями в зерне и границе [32]; разветвление одной границы на несколько (модель бамбуковых трубок, тройной стык) [20; 33]; разные скорости диффузии вдоль границ между зернами и между конгломератами зерен [34] и т.д. В настоящее время техника позволяет проводить вычисления и для более сложных структур, вид которых близок к структурам реальных материалов [35–37]. Для этих целей используют как построение структуры материала «вручную», так и генерацию случайно расположенных многогранников, например методом Вороного. И все же все эти уточнения в моделях неприменимы для описания зернограничной диффузии в материалах, где доля границ сопоставима с объемной долей зерен (наноразмерные материалы), поскольку в такой структуре границы не являются изолированными. Альтернативным способом исследования является симуляция вероятностного характера диффузии вдоль заданных границ, например методом Монте-Карло [38]. На уровне групп отдельных атомов и молекул аналогичную симуляцию проводят с использованием метода молекулярной динамики [39; 40]. Подобные исследования довольно часто применяют для сопоставления с экспериментом, когда невозможно однозначно учесть степень влияния различных факторов.
Для количественной оценки роли окисления так же, как и в [36; 37], стоит переходить от моделей изолированной границы к двумерным моделям с явно выделенными стыками границ. Размер зерен в наноструктурных материалах становится сопоставим с размером области влияния границ между ними и уже не представляет существенного препятствия на пути ускоренной диффузии. Настоящая работа является продолжением исследования зернограничной диффузии в материалах с нано- и микроструктурой [41–43] и до-полненна кинетикой образования оксидов в объеме зерен и граничной фазе.
1. Постановка задачи
Химические реакции, в том числе окисление, протекают при любой температуре, но с разными скоростями. При повышенных температурах процесс становится более заметным. Полагаем, что в условиях эксплуатации в агрессивной среде процесс окисления активируется при постоянной температуре, которую считаем известной. Полагаем, что на поверхности материала имеется атомарный кислород, который проникает вглубь материала посредством диффузии. Стадию диссоциации кислорода не рассматриваем. Поскольку наиболее активно диффузия идет по границам зерен, целесообразно при математическом моделировании процесса выделить области, примыкающие к границам зерен.
Полагаем, что образец имеет структуру, которая представлена двумя фазами (рис. 1): зёрнами (индекс B ) и окружающей их граничной фазой (индекс G ). Полагаем, что структура образца симметрична (на рис. 1 повторяющаяся область выделена пунктирными линиями). В направлении O x зерна имеют размер h x , а расстояние между соседними зернами 2Δ. Размер расчетной области l x в этом направлении может варьироваться. В направлении O y расчетная область включает половину размера зерна и половину расстояния между соседними зернами так, что общий размер расчетной области составляет l x ( h y + Δ). Выделенной структуре соответствует диффузионно-кинетическая задача в двумерной постановке.
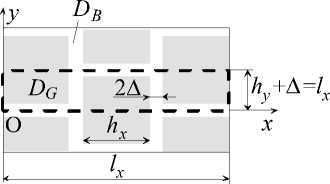
Рис. 1. Иллюстрация к постановке задачи
Уравнение диффузии кислорода с учетом его затрат на образование оксидов титана имеет вид:
∂ C ∂ t
d x d x
+ ^ D dC dy [ dy
- W ,
где С – концентрация (объемная доля) атомарного кислорода в титане, D – коэффициент диффузии, W – сток компонента за счет химических реакций. Уравнение имеет одинаковый вид и в зернах, и в граничной фазе.
Из всех возможных реакций окисления выберем три, приводящие к образованию наиболее устойчивых оксидов. Из диаграммы состояния «титан – кислород» видно, что с ростом концентрации кислорода в смеси будут образовываться оксиды титана в следующей последовательности: TiO → Ti 2 O 3 → TiO 2 :
-
1) Ti+O→TiO;
-
2) TiO+O→TiO 2 ;
-
3) 2TiO+O→Ti 2 O 3 .
Концентрации веществ обозначим следующим образом: [O] = С , [TiO] = C 1 , [TiO 2 ] = C 2 , [Ti 2 O 3 ] = C 3 ; [Ti] = C 4. Полагаем, что скорости реакции ω k зависят от концентраций в соответствии с законом действующих масс:
ц = .1 CC4; to2 = k2 CC1; to3 = k3 C (C1 )2, где kj – константа скорости химической реакции, j = 1, 2, 3 – номер реакции с образованием оксидов TiO, TiO2 и Ti2O3 соответственно. Тогда кинетические уравнения примут вид:
^C- = ц - м2 - 2to3,(2)
d t
=®2,(3)
a t d C3
—3 = ®3, a t а источниковое слагаемое в уравнении (1) вид:
W = to1 + to2 + to3, здесь ωj – скорость реакции.
Для материала образца (титан) из баланса массы получим:
C 4 = 1 - ( C + C + C 2 + C 3 ) .
Коэффициенты диффузии и константы скоростей реакций в фазах зерна ( G ) и границы ( B ) могут различаться. Обозначим D = D G ; k 1 = k 1 G ; k 2 = k 2 G ; k 3 = k 3 G – в зерне и D = D B ; k 1 = k 1 B ; k 2 = k 2 B ; k 3 = k 3 B – в границе зерна.
В начальный момент времени кислород и оксиды в материале образца отсутствуют:
t = 0: C = 0; C j ; C 4 = 1. (5)
На границе образца с окружающей средой концентрация кислорода задана и неизменна:
x = 0: C = C 0, (6)
где C 0 – концентрация диффузанта (кислорода) на границе образца с окружающей средой, содержащей кислород. Вдали от поверхности окисления источники и стоки кислорода отсутствуют:
d C x = lx ^ ^: — = 0. dx
Поскольку расчетная область обладает симметрией, на границах по оси y y = 0, y = ly = A + hy : — = 0. (8)
d y
На всех внутренних границах полагаем справедливыми условия идеального контакта. Имеем равенство химических потенциалов и потоков диффузанта (кислорода). Первое условие имеет вид gB = gG, где gB, gG – химический потенциал в граничной фазе и зерне соответственно.
Равенство химических потенциалов не означает равенство концентраций. В общем случае:
g ' = g 0 +— In ( C - y ( C k ) )
где γ ( C k ) – это коэффициенты активности, которые зависят от состава, т.е. от концентраций всех компонентов, i = G в зерне и i = B в границах между зернами. Это дает:
ln(C'Y(Ck ))|G = In(C'Y(Ck ))|B > или
( C Y ( C . ))| G = ( C Y ( C . ))| B -
Так как диффузант в модели один, то
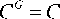
Y B ( C . ) Y G ( C . )
« C B y .
Здесь γ – коэффициент распределения. В простейшем случае γ заданная константа. Для простоты примем, что γ = 1 и считаем, что различия фаз проявляются в коэффициентах диффузии и скоростях реакции. Только тогда граничные условия на всех внутренних границах Γ между фазами принимают вид
Здесь, n – нормаль к границе Γ.
Таким образом, общая постановка задачи включает уравнения (1)–(4) и краевые условия (5)–(9).
-
2. Метод решения
Для удобства введем безразмерные переменные:
T = t/t. , ^ = x/A, Z = y/A , где t,=A2/Dg .
Теперь мы имеем размеры расчетной области L ξ = l x /Δ, L ζ = l y /Δ, размеры зерен h ξ и h ζ , расстояние между соседними зернами вдоль оси Oξ равное 2, вдоль оси Oζ – 1.
Уравнения (1)–(4) примут вид:
^ C =A Г D ^ C 1 +A Г D ^ C 1 - W , (10)
дт d^ L a^ J az L az J ’ ( )
W = ц + to 2 + to 3,
д C1__ _
—— — Ш| — to2 — 2 о.),; дт
д C _ д C _
2 — ^ 2 ; —3- — Ю з ; дт дт
C4 — 1 — (C + C1 + C2 + C3), где
Ю 1 — K 1 CC 4 ; Ю 2 — K 2 CC1 ; Ю 3 — K 3 C ( C 1 ) 2.
Краевые условия:
т — 0: С — 0; C j — 0; с 4 — 1; (12)
|
s — 0: С — C o ; |
(13) |
|
_ ЭС |
|
|
S— L ^^ : ^ С — 0; s s дs |
(14) |
|
Z — 0, Z — L z — 1 + h z : || — 0. |
(15) |
На всех внутренних границах между фазами
D G д n
— D B ^ C B г д n
; CG — CB . г
D — 5 - безразмерный коэффициент диффузии в фазах. В задаче содержатся следующие безразмерные параметры:
h s h x /А; h z— h y /А;
-
5 — Da/Da — 1; K 1 — A 2 k G^ D G ; K 2 — A 2 k G / DG ;
K 3 — A 2 k G D3G - в фазе зерна;
-
5 — D b/ D g — 1; K 1 — A 2 k B / D G ; K 2 — A 2 k BB / D G ;
K 3 — A 2 k 3 B /D G - в граничной фазе.
Интегральную концентрацию каждого из компонентов по всему объему рассчитывали по формуле:
L s L z
J — - J J C(s, Z) dsdz , (17)
S 0
где L ξ – размер расчетной области вдоль оси Oξ, L ζ – размер расчетной области вдоль оси Oζ, С – концентрация соответствующего компонента.
Задача решается численно. Используется разностная схема расщепления по координатам и метод прогонки. Все внутренние границы выделены явно. Для аппроксимации внутренних граничных условий используется разложение концентрации кислорода в точках разностной сетки, соседних с границей, в ряды
Тейлора относительно граничной точки по степеням шага разностной сетки. Это позволяет сохранить второй порядок аппроксимации во всех точках разностной сетки. Кинетические уравнения решаются с использованием алгоритма, описанного в [44] и подобного неявному методу Эйлера. Сходмость алгоритма проверяли сгущением разностной стеки. Точность расчетов составила 0,01.
3. Оценка значений безразмерных параметров
Размер зерен относительно размера границ оценим исходя из следующих фактов: минимальная погрешность измерения микроскопом составляет от 1 до 5 нм, размер зерен микрокристаллического оксида титана составляет от 50 до 10 мкм [45]. Следовательно, отношение размера зерен к расстоянию между соседними зернами можно оценить величиной h ξ = (10…2000).
Из справочной литературы [46] известны данные по диффузии кислорода в объеме материала. Для диффузии кислорода в титане в интервале температур от 1300 до 1500 К коэффициент диффузии в объеме имеет величину от 3.9·10–6 до 25.3·10–6 см2/с. Измерения величины коэффициента зернограничной диффузии для кислорода в титане отсутствуют. Однако для диффузии меди в никеле известны величины коэффициентов объемной и зернограничной диффузии [47] и их отношение составляет от 2 до 4·105. Полагаем, что и для диффузии кислорода в титане отношение коэффициента диффузии в границе и зерне δ имеет аналогичный порядок величин.
Величины констант химических реакций, протекающих в твердой фазе, оценить проблематично. Предложенные в литературе способы для теоретических оценок приводят к отличиям величин на порядки [48–50]. При экспериментальном определении точность существенно зависит от условий проведения эксперимента. Поэтому константы химических реакций будем варьировать. Согласно диаграмме состояния «титан – кислород» меньшей концентрации кислорода соответствует TiO, а с его увеличением появляются такие соединения, как Ti 2 O 3 , Ti 3 O 5 и TiO 2 . Следовательно, параметры модели необходимо выбрать таким образом, чтобы эта последовательность выполнялась.
4. Результаты расчетов
Полагаем, что концентрация кислорода на поверхности образца C0 = 0,05. Размеры зерен вдоль осей полагаем одинаковыми, так что на расчетную область приходится hξ = 10, hζ = 5. Размер расчетной области вдоль оси ξ выбираем исходя из того, что он должен охватывать как минимум пару зерен, но быть достаточным, чтобы на протяжении всего расчета выполнялось условие (14). При заданных параметрах это 6 зерен с прилегающими к ним границами: Lξ = 72, Lζ = 6. Для примера примем: δ = 1, K1 = 10, K2 = 2, K3 = 200 – в зер- не и δ = 100, K1 = 10, K2 = 2, K3 = 200 – в границе между зернами.
Если реакции протекают существенно медленнее, чем процесс накопления кислорода в результате диффузии (например при достаточно низкой температуре), реакциями можно пренебречь. На рис. 2 и 3 представлены профили распределения кислорода вдоль оси ξ, нормальной к поверхности (см. рис. 2) и в плоскости ξOζ (см. рис. 3). Из рисунка видно, что в отсутствие химических реакций концентрация кислорода С/С 0 = 0,1 к моменту времени τ = 5 достигается на глубине двух зерен, а концентрация С/С0 = 0,5 – на глубине только первого зерна.
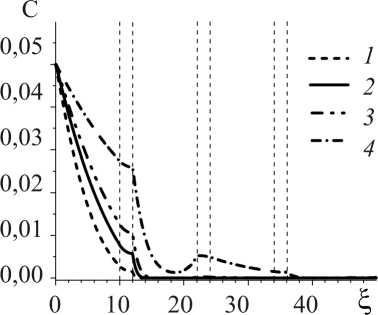
Рис. 2. Распределение концентрации кислорода вдоль координаты ξ при ζ = 0 в отсутствие реакций окисления в материале матрицы в моменты времени: τ = 1) 0,2; 2) 0,5; 3) 1,0; 4) 5,0. Вертикальные пунктирные линии показывают границы зерен
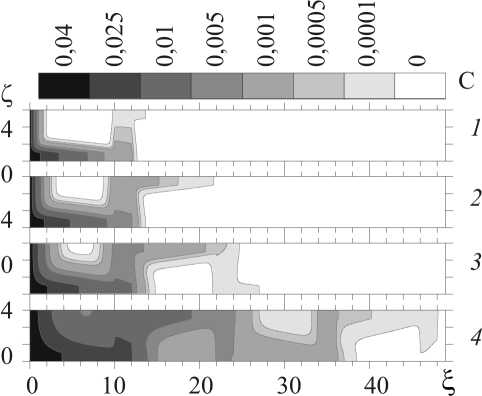
Рис. 3. Распределение концентрации кислорода в отсутствие реакций окисления в материале матрицы в моменты времени: τ = 1) 0,2; 2) 0,5; 3) 1,0; 4) 5,0
При повышении температуры активируются процесс окисления. Соотношение между скоростями реакций при разных температурах может быть различным. Сравним характеры окисления при одинаковых и различающихся константах реакций в зерне и граничной фазе (рис. 4–8). Очевидно, что часть кислорода тратится на образование оксидов. Часть оксида TiO также тратится на образование Ti2O3 и TiO2, что приводит к выраженному максимуму в распределении концентрации TiO (см. рис. 4). С уменьшением констант скорости реакций в фазе зерна распределение концентраций кислорода и оксидов вдоль границы изменяется незначительно (см. рис. 4), тогда как инте- гральная концентрация кислорода увеличивается, оксидов – уменьшается (см. рис. 5). Это связано с тем, что при уменьшении константы скорости реакции в фазе зерна наблюдается увеличение концентрации кислорода в фазе зерна, а продуктов реакции – в граничной фазе (см. рис. 6–8).
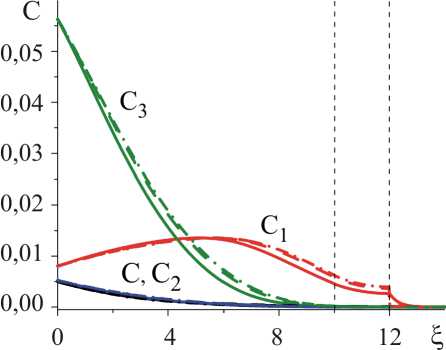
Рис. 4. Распределение концентрации кислорода и оксидов ξ при ζ = 0 в моменты времени τ = 5. Вертикальные пунктирные линии показывают границы зерен. [O] = С, [TiO] = C1, [TiO2] = C 2 , [Ti 2 O 3 ] = C 3 , в границе: K 1 = 10, K 2 = 2, K 3 = 200; в зерне: сплошные линии – K1 = 10, K2 = 2, K3 = 200; пунктирные линии – K1 = 1; K2 = 0,2, K3 = 20; штрихпунктирные линии – K 1 = 0,1, K 2 = 0,02, K 3 = 2
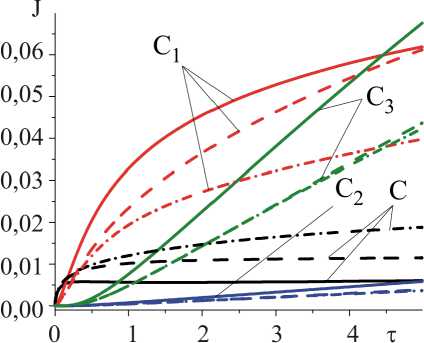
Рис. 5. Зависимость от времени интегральной концентрации, найденной по формуле (17) для кислорода и оксидов. [O] = С, [TiO] = C 1 , [TiO 2 ] = C 2 , [Ti 2 O 3 ] = C 3 , в границе: K 1 = 10, K 2 = 2, K3 = 200; в зерне: сплошные линии – K1 = 10, K2 = 2, K3 = 200; пунктирные линии – K1 = 1; K2 = 0,2, K3 = 20; штрихпунктир-ные линии – K1 = 0,1, K2 = 0,02, K3 = 2
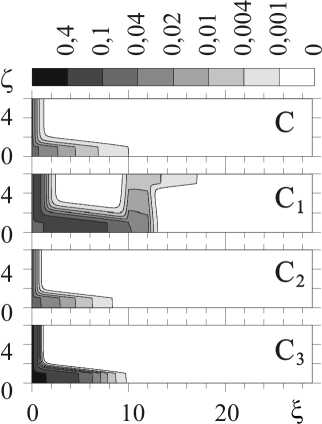
Рис. 6. Распределение концентрации кислорода в материале матрицы в момент времени τ = 5, [O] = С, [TiO] = C1, [TiO2] = C 2 , [Ti 2 O 3 ] = C 3 , в границе: K 1 = 10; K 2 = 2; K 3 = 200, в зерне: K 1 = 10; K 2 = 2; K 3 = 200
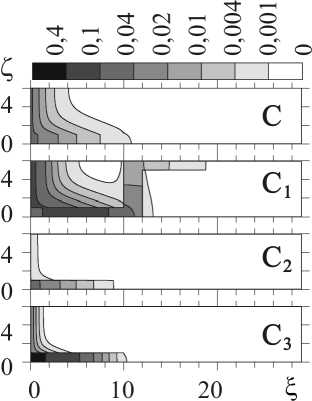
Рис. 7. Распределение концентрации кислорода в материале матрицы в момент времени τ = 5, [O] = С, [TiO] = C1, [TiO2] = C 2 , [Ti 2 O 3 ] = C 3 , в границе: K 1 = 10; K 2 = 2; K 3 = 200, в зерне: K 1 = 1; K 2 = 0,2; K 3 = 20
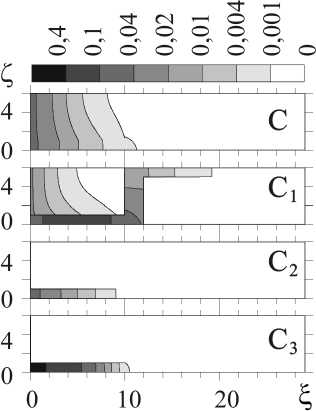
Рис. 8. Распределение концентрации кислорода в материале матрицы в момент времени τ = 5, [O] = С, [TiO] = C1, [TiO2] = C2, [Ti2O3] = C3, в границе: K1 = 10; K2 = 2; K3 = 200, в зерне: K 1 = 0,1; K 2 = 0,02; K 3 = 2
Если увеличить размеры зерна, то интегральная концентрация кислорода и оксидов снижается (рис. 9). Так, с увеличением размеров зерен в 1.5 и 2 раза относительно исходных к моменту времени τ = 5 интегральная концентрация кислорода снижается в 1,6 и 2,2 раза; TiO – в 1,8 и 2,6 раза; TiO 2 – в 1,9 и 3,1 раза; Ti 2 O 3 – в 2,0 и 3,2 раза.
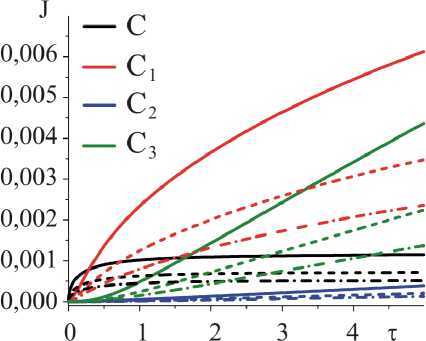
Рис. 9. Зависимость от времени интегральной концентрации, найденной по формуле (17) для кислорода и оксидов. [O] = С, [TiO] = C 1 , [TiO 2 ] = C 2 , [Ti 2 O 3 ] = C 3 , в границе: K 1 = 10; K 2 = 2;
K 3 = 200, в зерне: K 1 = 1; K 2 = 0,2; K 3 = 20
Видно, что характер зависимостей интегральных концентраций компонентов от времени не меняется.
Заключение
Таким образом, в работе представлена модель зернограничной диффузии с учетом окисления. Расчеты показывают, что в зависимости от значений константы скорости реакций в фазах зерна и границы окисление происходит преимущественно вблизи поверхности или вдоль границы зерен. С увеличением размеров зерен тенденции в процессе окисления не меняются. Следовательно, при существенно отличающихся свойствах зерен и граничной фазы будет наблюдаться преимущественное окисление вдоль границ зерен. Это может иметь разные последствия: 1) быстрое появление окисной пленки будет препятствовать дальнейшему проникновению кислорода вглубь материала; 2) разные свойства оксидов и основного материала могут служить причиной механических напряжений, которые впоследствии приведут к разрушению; 3) возможно и явление упрочнения поверхностного слоя вследствие появления в границах зерен оксидной фазе. Это требует дальнейшего исследования.
Список литературы Двумерная модель зернограничной диффузии и окисления
- Hydrogen Embrittlement Effects on Austenitic Stainless Steels with Ultrafine-Grained Structure of Different Morphology / E.G. Astafurova, E.V. Melnikov, S.V. Astafurov, I.V. Ratochka, I.P. Mishin, G.G. Maier, V.A. Moskvina, G.N. Zakharov, A.I. Smirnov, and V.A. Bataev // Physical mesomechanics. – 2019. – Vol. 22, № 4. – P. 313–326. doi 10.1134/S1029959919040076.
- Микроструктура и механические свойства внутреннеокис-ленных ванадиевых сплавов. II. Механические свойства, особенности пластической деформации и разрушения / А.Н. Тюменцев, Ю.П. Пинжин, С.В. Овчинников, И.А. Дитенберг, Н.В. Шевченко, А.Д. Коротаев, Я.В. Шуба, М.М. Потапенко, В.М. Чернов // Перспективные материалы. – 2005. – № 5. – С. 19–30.
- Шарифуллина Э.Р., Швейкин А.И., Трусов П.В. Обзор экспериментальных исследований структурной сверхпластичности: эволюция микроструктуры материалов и механизмы деформирования // Вестник Пермского национального исследовательского политехнического университета. Механика. – 2018. – № 3. – С. 103–127.
- Trusov P.V., Kondratyev N.S. Two-Level Elastoviscoplastic Model: An Application to the Analysis of Grain Structure Evolution under Static Recrystallization // Physical mesomechanics. – 2019. – Vol. 22, № 3. – P. 230–241. doi 10.1134/S1029959919030081.
- Особенности окисления субмикрокристаллического титана при нагревании в воздухе / А.В. Коршунов, А.П. Ильин, А.И. Лотков, И.В. Раточка, Т.П. Морозова, О.Н. Лыкова // Известия Томского политехнического университета. – 2011. – Т. 319, № 3. – С. 10–16.
- Кубашевский О., Гопкинс Б. Окисление металлов и сплавов. – М.: Металлургия, 1965. – 428 с.
- Unnam J., Shenoy R., Clark R. Oxidation of commercial purity titanium // Oxidation of Metals. – 1986. – Vol. 26, № 3/4. – Р. 231–252.
- Gemelli E., Camargo N. Oxidation kinetics of commercially pure titanium // Revista MatJria. – 2007. – Vol. 12, № 3. – P. 525–531.
- Хауффе К. Реакции в твердых телах и на их поверхности. – М.: Издатинлит, 1963. – Ч. 2. – 276 с.
- Реакционная способность субмикрокристаллического титана. I. Закономерности окисления при нагревании на воздухе / А.В. Коршунов, А.П. Ильин, А.И. Лотков, И.В. Раточка, Т.П. Морозова, О.Н. Лыкова // Перспективные материалы. – 2012. – № 4. – С. 5–12.
- Закономерности формирования структуры С-слоя, образующегося при синтезе рутила в процессах высокотемпературного окисления массивных титановых преформ / С.В. Шевцов, А.П. Стецовский, К.А. Шашкеев, В.Ю. Зуфман, Н.А. Аладьев, Л.И. Щворнева, К.А. Солнцев // Перспективные материалы. – 2010. – № 1. – С. 5–9.
- Овчинников И.Г., Кудайбергенов Н.Б., Дворкин М.С. Моделирование кинетики коррозии металлоконструкций с использованием банка математических моделей коррозии // Проблемы повышения надежности и долговечности конструкций зданий и сооружений: сб. науч. тр. Казахского химко-технологического института. – Шымкент, 1993. – С. 9–25.
- Локощенко А.М. Влияние масштабного фактора на длительную прочность // Проблемы прочности. – 1995. – № 3. – С. 13–18.
- Crank J. The Mathematics of Diffusion. – Oxford: Clarendon Press, 1975. – 414 p.
- Lokoshchenko A.M. Creep and Creep Rupture of Metals. Boca Raton. London. – New York: CRC Press Taylor & Francis Group. 2018. – 546 p.
- Lokoshchenko A.M., Kulagin D.A. Diffusion locking effect on long-term Strength // Moscow University Mechanics Bulletin. – 2014. – Vol. 69. № 5. – P. 123–125.
- Вильчевская Е.Н., Фрейдин А.Б., Морозов Н.Ф. Кинетика фронта химической реакции в центрально-симметричных задачах механохимии // Доклады РАН. – 2015. – Т. 461, № 5. – С. 525–529.
- Collected works of Eshelby J.D. Mechanics of Defects and Inhomogeneities (Solid Mechanics and its Applications) / eds. K. Markenscoff, A. Gupta. – Berlin. Springer. 2006. – 930 p.
- Sedlak M., Alfredsson B., Efsing P. A coupled diffusion and cohesive zone model for intergranular stress corrosion cracking in 316L stainless steel exposed to cold work in primary water conditions // Engineering Fracture Mechanics. – 2019. – Vol. 217. – P. 106543.
- Ogurtani T.O., Oren E.E. Irreversible thermodynamics of triple junctions during the intergranular void motion under the electromigration forces // International Journal of Solids and Structures. – 2005. – Vol. 42, iss. 13. – P. 3918–3952.
- Atmospheric corrosion: A review focussed on modelling / H. Simillion, O. Dolgikh, H. Terryn, J. Deconinck // Corrosion Reviews. – 2014. – Vol. 32 (3–4). – P. 73–100.
- Deconinck D., Van Damme S., Deconinck J. A temperature dependent multi-ion model for time accurate numerical simulation of the electrochemical machining process. Part I: Theoretical basis // Electrochimica Acta. – 2012. – Vol. 60. – P. 321–328.
- Deconinck D., Van Damme S., Deconinck J. A temperature dependent multi-ion model for time accurate numerical simulation of the electrochemical machining process. Part II: Numerical simulation. // Electrochimica Acta. – 2012. – Vol. 69. – P. 120–127.
- Malki B., Baroux B. Computer simulation of the corrosion pit growth // Corrosion Science. – 2005. – Vol. 47 (1). – P. 171–182.
- Herzig C., Divinski S.V. Grain Boundary Diffusion in Metals: Recent Developments. Materials Transactions. – 2003. – Vol. 44, № 1. – P. 14–27.
- Grain boundaries in ultrafine grained materials processed by severe plastic deformation and related phenomena / X. Sauvage,G. Wilde, S. Divinsky, Z. Horita, R.Z. Valiev // Materials Science and Engineering A. – 2012. – Vol. 540. – P. 1–12.
- Fisher J.C. Calculation of Diffusion Penetration Curves for Surface and Grain Boundary Diffusion // Journal of Applied Physics. – 1951. – Vol. 22, iss. 1. – P. 74–77.
- Kaur. I., Gust W. Fundamentals of Grain and Interphase Boundary Diffusion. – Stuttgart: Ziegler Press, 1989.
- Nazarov A.A. Grain-boundary diffusion in nanocrystals with a time-dependent diffusion coefficient // Physics of the Solid State. – 2003. – Vol. 45, № 6. – P. 1166–1169.
- Krasil'nikov V.V., Savotchenko S.E. Grain boundary diffusion patterns under nonequilibrium and migration of grain boundaries in nanoctructure materials // Bulletin of the Russian Academy of Sciences: Physics. – 2009. – Vol. 73, № 9. – P. 1277–1283.
- Gibbs G.B. Grain Boundary Impurity Diffusion // Physica status solidi (b). – 1966. – Vol. 16, № 1. – P. K27-K29.
- Popov V.V. Model of grain-boundary diffusion with allowance for near-boundary layers of equilibrium composition // The Physics of Metals and Metallography. – 2006. – Vol. 102, № 5. – P. 453–461.
- Aleshin A.N. Diffusion in an Ensemble of Intersecting Grain Boundaries Forming a Triple Junction // Russian metallurgy (Metally). – 2009. – Vol. 2009, № 5. – P. 394–399.
- Zhang S. Size-dependent Diffusion Coefficient in Nanocrystalline Materials // Advanced Materials Research. – 2012. – Vol. 391–392. – P 418–421.
- A numerical model coupling diffusion and grain growth in nanocrystalline materials / J. Zhao, G.-X. Wang, C. Ye, Y. Dong // Computational Materials Science. – 2017. – Vol. 136. – P. 243–252.
- The Harrison diffusion kinetics regimes in solute grain boundary diffusion / I.V. Belova, T. Fiedler, N. Kulkarni, G.E. Murch // Philosophical Magazine. – 2012. – Vol. 92, № 14. – P. 1748–1763.
- Миколайчук М.А., Князева А.Г. Модель диффузии примеси в структурно-неоднородной деформируемой среде // Известия высших учебных заведений. Физика. – 2012. – № 5/2. – С. 74–80.
- Изучение влияния механических напряжений на диффузию в пластине с покрытием / М.А. Миколайчук, А.Г. Кнзева, Г.П. Грабовецкая, И.П. Мишин // Вестник ПНИПУ. Механика. – 2012. – № 3. – С. 131–135.
- Saha S., Motalab M. Nature of creep deformation in nanocrystalline Tungsten // Computational Materials Science. – 2018. – Vol. 149. – P. 360–372.
- Lipnitskii A.G., Nelasov I.V., Kolobov Yu.R. Molecular dynamics study of grain boundary self-diffusion in hcp and bcc nanocrystalline titanium // Physical mesomechanics. – 2013. – Vol. 16, № 1. – P. 67–73.
- Чепак-Гизбрехт М.В. Влияние тройных стыков и размера зерен на диффузию кислорода в поверхностный слой материала // Известия высших учебных заведений. Физика. – 2021. – Т. 64, № 4 (761). – С. 50–55.
- Chepak-Gizbrekht M.V., Knyazeva A.G. Grain-boundary diffusion modeling in a microstructural material // Computational Materials Science. – 2020. – Vol. 184. – P. 109896.
- Knyazeva A.G. The theory of reactive diffusion for the description of oxide phase growth in a coating // AIP Conference Proceedings. – 2015. – Vol. 1683. – P. 020084.
- Demidov V.N., Knyazeva A.G. Multistage kinetics of the synthesis of Ti–TxCy composite // Nanoscience and Technology: An International Journal. – 2019. – Vol. 10, Iss. 3. – P. 195–218.
- Севидова Е.К., Симонова А.А. Особенности коррозионно-электрохимического поведения титана с нано- и субмикрокристаллической структурой // Электронная обработка материалов. – 2011. – Т. 47, № 2. – С. 70–75.
- Landolt-Bornstein Numerical Data and Functional Relationships in Science and Technology. New Series. Group III: Crystal and Solid State Physics. Vol. 26 Diffusion in Solid Metals and Alloys / editor H. Mehrer; editor in Chief: O. Madelung. – Berlin Heidelberg Springer-Verlag, 1990.
- Роль диффузионно-контролируемых процессов в формировании структуры и свойств металлических наноматериалов / Ю.Р. Колобов, А.Г. Липницкий, М.Б. Иванов, Е.В. Голосов // Композиты и наноструктуры. – 2009. – № 2. – С. 5–24.
- Даниэльс Ф., Олберти Р. Физическая химия. – М.: Мир, 1978. – 648 с.
- Binnewies M., Milke E. Thermochemical Data of Elements and Compounds. – Weinheim: Wiley-VCH Verlag GmbH, 2002.
- Термодинамические свойства неорганических веществ: справочник / У.Д. Верятин, В.П. Маширев, Н.Г. Рябцев, В.И. Тарасов, Б.Д. Рогозин, И.В. Коробов. – М.: Атомиздат, 1965. – 461 с.


