Двумерные ускоряющиеся бесселевы пучки

После открытия пучков Эйри с конечной энергией [1] возрос интерес к световым пучкам с искривлённой траекторией. Пучки Эйри распространяются по параболической траектории и демонстрируют такие свойства, как бездифракционность и самовосстановление после искажения препятствиями. Пучки Эйри до сих пор активно исследуются: в [2] рассматриваются симметричные пучки Эйри, в [3] изучается влияние астигматизма на вид пучка Эйри. В [4] изучается трёхмерный пучок Эйри с произвольным углом между «двумя крыльями», а в [5] рассмотрена спиральная фокусировка пучков Эйри с оптическим вихрем. Кроме пучков Эйри, рассматривались и другие непараксиальные ускоряющиеся световые пучки с произвольной поперечной формой [6]. Однако пучки Эйри параксиальны, их комплексная амплитуда является решением уравнения Гельмгольца в параксиальном приближении (уравнения типа Шрёдингера). В связи с этим в последние годы предпринимались попытки преодолеть параксиальное ограничение и найти решения точного уравнения Гельмгольца, описывающие ускоряющиеся световые пучки [7, 8] способные поворачивать при распространении на большие углы, чем параксиальные пучки. Из любого точного решения трёхмерного уравнения Гельмгольца, описывающего бездифракционный световой пучок, можно получить решение двумерного уравнения Гельмгольца. Для этого достаточно константу распространения принять равной нулю. Так, в работе [8] за основу взяты решения в виде пучков Матье и Вебера, а в [7] – моды Бесселя, но угловой спектр плоских волн был усечён, что привело к формированию светового пучка с траекторией в виде полукольца. В недавней работе [9] предложено преобразовывать с помощью зеркала световое поле от точечного источника в поле с круговой каустикой длиннее, чем полукольцо. Но полного кольца достигнуто до сих пор не было. В этой работе предлагается формировать двумерный пучок Бесселя таким образом, чтобы сформировать световое кольцо, по которому свет циркулирует непрерывно.

Ещё один недостаток пучков Эйри, как и многих других световых пучков, состоит в том, что распределение интенсивности в поперечном сечении, помимо главного максимума, имеет вспомогательные максимумы (боковые лепестки). В ряде работ рассматриваются методы подавления боковых лепестков. Так, в [10] предложено использовать конический аксикон для подавления этих лепестков в дальней зоне дифракции плоской волны на спиральной фазовой пластинке, ограниченной круглой диафрагмой. В [11] на основе векторных формул Дебая рассчитана кольцевая амплитудная маска для подавления боковых лепестков у радиально поляризованного остросфокуси-рованного пучка Лагера–Гаусса. В [12] используется асимметричная аподизация Фурье-спектра для усиления главного максимума интенсивности и подавления боковых лепестков у пучков Эйри.

В данной работе мы, по аналогии с работой [7], рассмотрим двумерный Бесселев пучок, однако с помощью двух источников, расположенных друг напротив друга, будет сформировано световое кольцо, которое можно считать ускоряющимся световым пучком, поворачивающим на угол 360 градусов.

Кроме того, в данной работе рассматривается решение двумерного уравнения Гельмгольца, которое так же, как и пучки в [7, 8], получено из решения трёхмерного уравнения Гельмгольца, описывающего бездифракционный пучок. Но, в отличие от [7, 8], вместо стандартного пучка Бесселя за основу взято решение для асимметричного пучка Бесселя [13, 14]. Показано, что это решение может быть получено из традиционного пучка Бесселя путём вещественного сдвига вдоль одной декартовой координаты и мнимого сдвига вдоль другой, как это предлагается в работе [15]. Также показано, что с ростом параметра асим- метрии светового пучка, комплексная амплитуда которого описывается найденным решением, уменьшается его расстояние распространения, но при этом падает и интенсивность боковых лепестков.

En (x, z) = Jn I k^x2 +(z - z0 )2 Ix

x exp

in arctg

z

-

z ₀

1. Моделирование формирования кольцевого 2D пучка Бесселя FDTD-методом

Двумерное уравнение Гельмгольца имеет вид:

d ² E 1 d E d ² E

—_r +--+ — + k k ² E = 0,

dr2 r dr Эф2

где ( r , ф ) - полярные координаты в плоскости Oxz ( x = r cos ф , z = r sin ф ), k = 2 п / % - волновое число для света с длиной волны % . В разделяющихся переменных это уравнение имеет решение

E n ( r , ф ) = J n ( kr ) exp ( in ф ) ,

где n – целое число (порядок моды Бесселя). Световое поле с комплексной амплитудой (2) можно представить как суперпозицию плоских волн:

E. ( x,=^x

2 n

2п x J exp (in 6 + ikx cos 6 + ikz sin 6) d6.

Легко видеть, что поле (3) состоит из плоских волн, которые имеют всевозможные направления, так как угол 6 , который определяет направление их распространения, меняется от 0 до 2 п . Поле (3) можно представить в виде:

E n ( x , z ) = E „ ⁺( x , z ) + E ;( x , z ) ,                      (4)

E±( x, z ^■(ТП- x где

П xJ exp (in 6 ± ikx cos 6 ± ikz sin 6) d6.

Поле (5) может быть представлено в виде ряда из функций Бесселя, Ангера и Вебера:

E ± ( x , z   ^2 x

+^

^X E ( ± i T ^J m ( kx ) [ ^J n - m ( ^T kz ) ^{+ E} n - m ( ^{T k}z ) ] , m =-^

x

нельзя сформировать, если в начальной плоскости z =0 задать комплексную амплитуду в виде

^E n ( ^{x ,0} ) = J n ( k^X^ + z O ) exp

, I z„

- in arctg I —

I x

В этом случае вместо светового кольца будет сформирована только его часть (почти полукольцо). Так, на рис. 1 показаны распределения интенсивности в плоскости Oxz , рассчитанные с помощью интеграла (3), но на рис. 1 а нижний и верхний пределы интегрирования равны соответственно 0 и 2 п , а на рис. 1 б -0 и п (т.е. на рис. 1 б показана величина | E + ( x , z ) |²). Рис. 1 получен для % = 532 нм, n = 20, -2 % < x , z < 2 % .

а)

Рис. 1. Распределения интенсивности в плоскости Oxz, рассчитанные с помощью интеграла (3) для разных значений пределов интегрирования: от 0 до 2 п (а), от 0 до п (б) (точки в центре - начала координат)

Поэтому для формирования светового кольца требуется, чтобы плоские волны распространялись вдоль оптической оси как в положительном направлении, так и в отрицательном.

Если начальное поле задать в плоскости, проходящей через центр кольца, то сформируется полукольцо, показанное на рис. 2 а . Рис. 2 а получен путём численного моделирования конечно-разностным FDTD-методом, когда начальное поле задавалось в виде (TE-поляризация, т.е. E_y ≠ 0):

б)

где J/ z ) и E p ( z ) - функции Ангера и Вебера:

1 ?

Jv (z) =    cos(v6-zsin6)d6,п 0

1 r

Ev (z) =    sin(v6-zsin6)d6.

п 0

Поле E_n ( x , z ) распространяется в отрицательном

направлении оси z . Это означает, что поле (2), смещённое на некоторую величину z ₀ вдоль оптической

оси, т.е. поле вида

E y ( x , z = 0 ) = J n ( kx )                              (10)

при n = 20. Остальные параметры были равны: область моделирования: -60 % < x , z < 60 % , 0< z <40 % , время моделирования - 100 % / c , шаг дискретизации по обеим координатам - % /32, а по времени - % /(64 c ).

Если начальное поле сместить от центра кольца и задать его в виде (9), то будет сформировано полукольцо, показанное на рис. 2 б .

Чтобы сформировать кольцо вместо полукольца, напрашивается встречное распространение двух Бесселевых пучков (8). В этом случае действительно формируется световое кольцо, однако в результате интерференции на кольце ярко выражены существенные провалы интенсивности (рис. 2 в ).

а)

б)

Рис. 2. Распределение усреднённой по времени интенсивности светового поля в плоскости Oxz с начальной комплексной амплитудой (10) (а) и (9) (б), а также в случае встречного распространения двух световых полей (8) (в) (точки внизу – начала координат)

Чтобы сформировать кольцо с постоянной интенсивностью, также моделировалось распространение полей (4) от двух источников, расположенных на расстоянии 10 1 друг напротив друга. В плоскости z = 0 комплексная амплитуда была задана в виде

(- i))

E ( x, z = 0 ) = E ( x, - z o ) =      x2п

п xj exp (in 6 + ikx cos 6 - ikz0 sin 0) d6,

а в плоскости z = 2 z ₀= 10 1 комплексная амплитуда была задана симметрично в виде E ( x , z = 2 z ₀) = E (– x , z = 0). Распределение амплитуды и фазы поля (11) показано на рис. 3.

Эти два линейных источника генерируют пучки, распространяющиеся навстречу друг другу, и формируют двумерный Бесселев пучок с центром в точке x = 0, z0 = 51. Остальные параметры были равны: область моделирования: -1001 < x, z < 1001, 0 < z < 101, время моделирования - 1001/c, шаг дискретизации по обеим координатам - 1/64, а по времени - 1/(128c). На рис. 4 показана усреднённая по времени интен- сивность сформированного двумерного Бесселева пучка с топологическим зарядом n =20. Оставшаяся небольшая неравномерность распределения интенсивности на световом кольце объясняется конечными размерами обоих источников света.

А, отн.ед.

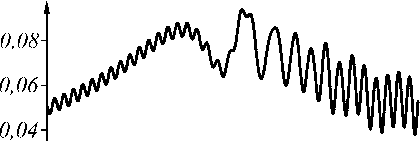
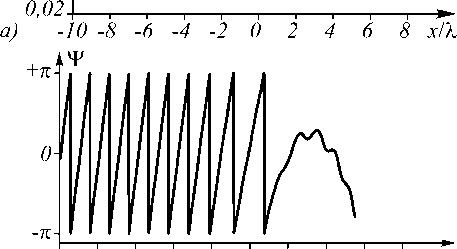
Рис. 3. Амплитуда А(а) и фаза ^ (б) поля (11)

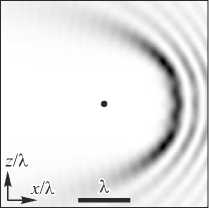
Рис. 4. Усреднённая по времени интенсивность двумерного Бесселева пучка, рассчитанная FDTD-методом (стрелками показаны направления распространения света от источников, точка внизу – начало координат)

На рис. 5 показано распределение величины потока мощности в плоскости z =5 1 (рис. 5 а ) и в плоскости x =0 (рис. 5 б ).

Р, отн.ед. 0,020,01-

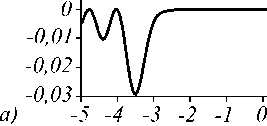
Р, отн.ед.

0,01-

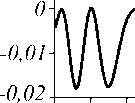
JV

7 2 3 4 хТх

1234 zk

Рис. 5. Распределение величины потока мощности в плоскостях z = 5 1 (а) и x = 0 (б)

Из рис. 5 следует, что поток световой мощности распространяется по световому кольцу (рис. 4) против часовой стрелки.

2. Моделирование распространения двумерного асимметричного пучка Бесселя

В работах [13, 14] рассмотрены асимметричные непараксиальные моды Бесселя, являющиеся точным решением трёхмерного скалярного уравнения Гельмгольца. Аналогичное решение двумерного уравнения Гельмгольца можно получить, если поперечную ко-

вания -60 X <  x < 60 X , 0 <  z < 40 X , шаг дискретизации по обеим декартовым координатам - X /32, по времени - X /(64 c ), где c - скорость света в вакууме. В качестве начального поля в плоскости z =0 задавалась сле-

дующая комплексная амплитуда (TE-поляризация):

Ey (x, z = 0) =

ординату y заменить на продольную координату z , а масштабирующий параметр Бесселева пучка принять равным волновому числу k :

J n ( kx ) , x >  0, 0, x <  0.

E n ( x , z ; c ) =

kr

kr - 2 c exp ( i ф )

x J_n {^ kr [ kr - 2 c exp ( i ф ) J } exp ( in ф ) ,

где ( r , ф ) - полярные координаты в плоскости Oxz . Переходя к декартовым координатам, получим выра-

Рис. 6. Распределение в плоскости Oxz усреднённой по времени интенсивности пучка с начальной комплексной амплитудой (16)

жение для комплексной амплитуды:

En (x.z;c ) =

k (x + iz )2 k (x2 + z2) - 2 c (x + iz)

- n / 2

x

J (13)

x Jn {Jk2 (x2 + z2) - 2kc (x + iz

Заметим, что пучок (13) совпадает с (10) при c =0 и z =0.

Известен способ получения решений уравнения Гельмгольца методом комплексного смещения источ-

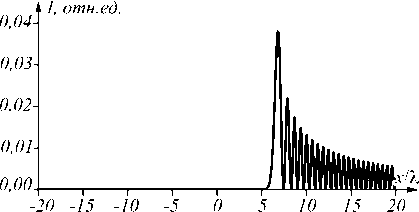
Рис. 7. Распределение интенсивности пучка (16) в плоскости z = 0

ника. Эта идея возникла ещё в 1967 году, когда Кравцов [16] показал, что поле точечного источника с мнимым расположением в параксиальном приближении сводится к параксиальному Гауссову пучку. Позже этот метод развивался в работах [17–19]. В данной работе покажем, что решение (13) также может быть получено из комплексной амплитуды обычного Бесселева пучка, но ось которого смещена по оси x на действительную величину, а по оси z – на мнимую. Для

этого введём две комплексные координаты: f u = x - c/k ,

[ v = z - ic/ k .

Тогда (13) преобразуется следующим образом:

En ( u, v ) =

u + iv

u2 + v v

n

J n

( k^u ²+ v ²).

Если бы координаты u и v были вещественными, выражение (15) описывало бы комплексную амплитуду традиционного Бесселева пучка в декартовых координатах.

На рис. 6 показано распределение усреднённой по времени интенсивности в плоскости Oxz двумерного пучка Бесселя, а на рис. 7 – распределение интенсивности этого же пучка в плоскости z =0. Рис. 6 и 7 получены путём численного моделирования конечно-разностным FDTD-методом ( Finite difference in time-domain ) решения системы уравнений Максвелла для следующих значений параметров: длина волны X = 532 нм, порядок функции Бесселя n =40, область моделиро-

Из рис. 6 и 7 видно, что у поля с распределением в начальной плоскости (16), помимо главного максимума интенсивности, имеется множество побочных максимумов. Интенсивность второго максимума составляет 57 % от интенсивности главного максимума.

Для того, чтобы уменьшить контраст боковых лепестков, вместо поля (16), можно использовать поле (13) при z =0 и разных значениях параметра асимметрии c . В начальной плоскости комплексная амплитуда такого поля имеет вид:

n 2

I J n { ^fcx ( kx - 2 c ) } . (17)

На рис. 8 а , б показано полученное FDTD-методом распределение усреднённой по времени интенсивности в плоскости Oxz двумерного асимметричного пучка Бесселя с начальным полем (17) для следующих значений параметра асимметрии: c = 1 (рис. 8 а ) и c =2 (рис. 8 б ). Значения остальных параметров те же, что и на рис. 6 и 7. На рис. 9 показаны распределения интенсивности этих же пучков в плоскости z = 0.

Интенсивность второго максимума на рис. 9 а составляет 45 % от интенсивности главного максимума, а на рис. 9 б – 35 %. Интенсивность второго максимума по отношению к главному также вычислялась для c = 0,5; полученная зависимость оказалась почти линейной и показана на рис. 10. Из рис. 10 следует, что

величину второго максимума можно снизить с 57 % до 20 %, т.е. почти в 3 раза.

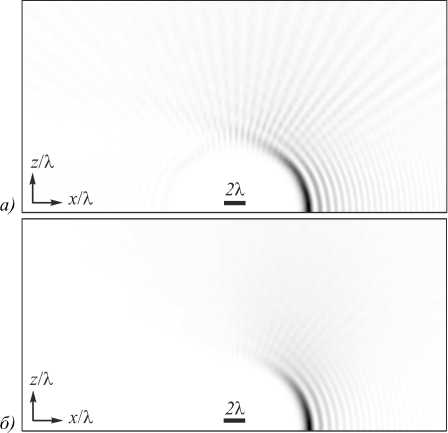
Рис. 8. Распределения усреднённой по времени интенсивности пучка с начальным распределением (17) в плоскости Oxz при c = 1 (а) и c = 2 (б)

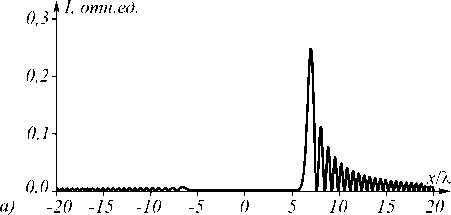
б)

Рис. 9. Распределение интенсивности пучка (13) в плоскости z = 0 при c = 1 (а) и c = 2 (б)

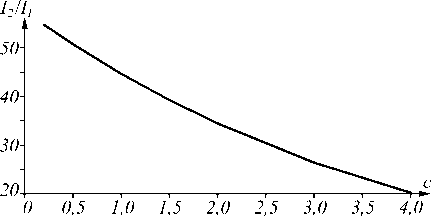
к интенсивности главного максимума от параметра асимметрии c

Рис. 10. Зависимость интенсивности второго максимума

Из сравнения рис. 6 и 8 видно, что длина распространения пучка с ростом параметра асимметрии c спадает. Определим эту длину как расстояние z ₁, на котором интенсивность спадает в два раза:

max | e ( x, z 1 )|

= 2 max | e ( x ,0 )|.

На рис. 11 приведена зависимость длины распространения пучка от параметра асимметрии c .

Из рис. 11 видно, что, хотя с ростом параметра асимметрии c двумерного пучка Бесселя (13) относительная величина боковых лепестков уменьшается, но и длина траектории тоже уменьшается (но медленнее).

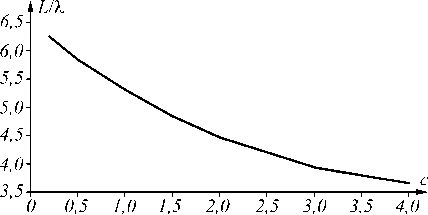
Рис. 11. Зависимость длины светового пучка (по полуспаду интенсивности) от параметра асимметрии c

Заключение

В работе получены следующие результаты:

– показано, что если два двумерных пучка, комплексная амплитуда которых описывается рядом из функций Бесселя, Ангера, Вебера, направить навстречу друг другу, то сформируется световое кольцо , по которому циркулирует поток мощности (уравнения (4)–(6));

– аналитически показано, что асимметричная мода Бесселя получается путём смещения традиционной моды Бесселя вдоль декартовых координат, причём вдоль одной координаты смещение – мнимая величина (уравнение (15));

– получено решение двумерного уравнения Гельмгольца, описывающее двумерный ускоряющийся асимметричный Бесселев пучок (уравнение (12));

– численно показано, что с ростом параметра асимметрии двумерного асимметричного Бесселева пучка уменьшается расстояние распространения пучка, но также снижается величина бокового лепестка по отношению к главному лепестку (рис. 10 и 11).

Работа выполнена при поддержке Министерства образования и науки РФ, грантов Президента РФ поддержки ведущих научных школ (НШ-3970.2014.9) и молодого доктора наук (МД-1929.2013.2), а также грантов РФФИ 13-07-97008 и 14-07-31092.