Dynamic Adaptive Median Filter (DAMF) for Removal of High Density Impulse Noise
Автор: Punyaban Patel, Banshidhar Majhi, Bibekananda Jena, C.R.Tripathy
Журнал: International Journal of Image, Graphics and Signal Processing(IJIGSP) @ijigsp
Статья в выпуске: 11 vol.4, 2012 года.
Бесплатный доступ
This paper proposes a novel adaptive filtering scheme to remove impulse noise from images. The scheme replaces the corrupted test pixel with the median value of non-corrupted neighboring pixels selected from a window dynamically. If the number of non-corrupted pixels in the selected window is not sufficient, a window of next higher size is chosen. Thus window size is automatically adapted based on the density of noise in the image as well as the density of corruption local to a window. As a result window size may vary pixel to pixel while filtering. The scheme is simple to implement and do not require multiple iterations. The efficacy of the proposed scheme is evaluated with respect to subjective as well as objective parameters on standard images on various noise densities. Comparative analysis reveals that the proposed scheme has improved performance over other schemes, preferably in high density impulse noise cases. Further, the computational overhead is also less as compared its competent scheme.
Impulse Noise, Image Denoising, Adaptive filter, Peak Signal-to-Noise Ratio (PSNR)
Короткий адрес: https://sciup.org/15012460
IDR: 15012460
Текст научной статьи Dynamic Adaptive Median Filter (DAMF) for Removal of High Density Impulse Noise
Published Online September 2012 in MECS
Noise suppression from images is still remains as one of the challenges among researchers. Impulsive noise in images is predominant during acquisition, storage and transmission. It occurs in two types either as fixed valued (salt and pepper) or random valued. In salt and pepper case the corrupted pixels assumes the maximum or minimum gray level, whereas in random valued impulse noise the corrupted pixel will be any value within the dynamic range of minimum or maximum gray level. The main thrust in any filtering scheme is to remove the impulsive noise while preserving the image details in restored images. The existing impulse noise removal schemes are classified into two categories, namely filtering without detection and detection prior to filtering. The nonlinear standard median filter (SMF) [1] falls under the first category. It is computationally efficient and simple to implement, but it performs poorly in high density impulse noise. Further, the filters under the first category perform filtering operation on all pixels of an image irrespective of its corruption status and as a result the restored image suffers from loss of edges and other image details. On the other hand, the second category of filters detects a pixel under consideration to be corrupted or not. Subsequently, it applies a filtering operation on the corrupted pixels only keeping the non-corrupted one’s intact. This selective filtering shows superior performance in restored images. Progressive switching median filter (PSMF)[2], Adaptive median filter (AMF) [3], minimum-maximum exclusive mean (MMEM) [4] are few such schemes which perform well in low as well as high density impulse noise. The progressive switching median filter (PSMF) achieves the detection and removal of impulse noise in two separate stages. In first stage, it applies impulse detector and then the noise filter is applied progressively in iterative manner in the second stage. In this method, impulse pixels located in the middle of large noise blotches can also be properly detected and filtered. The performance of this method is not good for very high density noise cases. Adaptive median filter (AMF) is used for discriminating corrupted and uncorrupted pixels and then applies the filtering technique. Noisy pixels are replaced by the median value, and uncorrupted pixels are left unchanged. It performs well at low noise densities but at higher noise densities, window size has to be increased to get better noise removal which will lead to less correlation between corrupted pixel values and replaced median pixel values. The minimum-maximum exclusive mean (MMEM) filter uses mean value instead of median values of neighboring pixels to remove impulse noise from highly corrupted images. Simulation results show that even if the occurrence rate of the impulse noise is very high (70%), the restoration performance is still acceptable. A noise adaptive soft switching median (NASM) filter [6] is suggested, where a three-level hierarchical soft-switching noise detection process is used. An efficient decision-based algorithm (EDBA) [7] and subsequently its improved version an improved decision-based algorithm (IDBA) [8] have been proposed to combat the high density impulse noise. The decision-based algorithm (DBA) uses a fixed window size of 3 × 3, where the corrupted pixels are replaced by either the median pixel or neighborhood pixels. It shows promising result with lower processing time which degrades the visual quality of the image as the noise density increased. To overcome this problem, an improved decision-based algorithm (IDBA) is proposed where corrupted pixels can be replaced either by the median pixel or, by the mean of processed pixels in the neighborhood. It results in a smooth transition between the pixels with edge preservation and better visual quality for low-density impulse noise. A novel robust estimation based filter (REBF)[9] and a modified decision based unsymmetric trimmed median filter (MDBUTMF)[10] have been proposed recently to deal with high density impulse noise. The function of the robust estimation based filter (REBF) filter is to detect the outlier pixels and restore the original value using robust estimation. The Modified Decision Based Unsymmetric Trimmed Median Filter (MDBUTMF) replaces the noisy pixel by trimmed median value when other pixel values, 0’s and 255’s are present in the selected window and when all the pixel values are 0’s and 255’s then the noise pixel is replaced by mean value of all the elements present in the selected window.
It has been observed that most of the schemes use a fixed size window for filtering of corrupted pixels. The size of window is larger in high density impulse noise and smaller in low density noise. But no schemes addresses a selection of a dynamic window for a test pixel based on the density of corruption in its neighbor pixels. Few recently published articles like MDBUTMF, REBF, IDBA etc. replaces the current pixel with the mean value of the pixels in a fixed window when there do not exist nonzero number of noise free pixels. This introduces blurring in the restored images and noise elimination could not be made completely. To alleviate these limitations, in this paper, we propose a Dynamic Adaptive Median Filter (DAMF) for removing high density salt and pepper noise. The filter is dynamic in nature as it decides the window size for the test pixel locally before filtering during run time and is adaptive due to the selection of a proper window size. The exhaustive simulation along with comparative analysis with the existing schemes in low as well as high density impulse noise shows the strength of the proposed scheme.
The paper is organized as follows; the impulse noise model is given in section II, Section III deals with the proposed scheme. In Section IV, the simulation results along with comparative analysis are discussed in detail. Finally, Section V gives the concluding remarks.
Figure-1 may best describe the difference between SPN and RVIN. In the case of SPN the pixel substitute in the form of noise may be either L min (0)orL ma.,. (255) . Where as, in RVIN situation it may range from LmintoLmax . Cleaning such noise is far more difficult than cleaning fixed-valued impulse noise since for the later, the differences in gray levels between a noisy pixel and its noise-free neighbors are significant most of the times. In this paper, we focus only on salt and pepper noise and schemes are proposed to suppress such noise.

0 {0,255} 255
(a)

0 [0,255] 255
-
II. NOISE MODEL
(b)
Impulsive noise can be classified as salt-and-pepper noise (SPN) and random-valued impulse noise (RVIN). An image containing impulsive noise can be described as follows:
( ,-D = {.
p (t, ) ) w i th p г о b a. b i I i ty p у (i, j) wi tt prob ah iI tty 1-p
x ( i, j ) denotes a noisy image pixel, y( i,)) denotes a noise free image pixel and ?]( i ,) denotes a noisy impulse at the location(i ,) ). In salt-and-pepper noise, noisy pixels take either minimal or maximal values i.e. p (i J) £ {L mln , Lmax} and for random-valued impulse noise, noisy pixels take any value within the range minimal to maximal value i.e. ?]( i, ) £ [L miTl , L max^, where L m ln, Lmax denote the lowest and the highest pixel luminance values within the dynamic range respectively. So that it is little bit difficult to remove random valued impulse noise rather than salt and pepper noise [3]. The main difficulties, which have to face for attenuation of noise, is the preservation of image details.
Figure 1: Representation of (a) Salt & Pepper Noise with R jj £ [nmin,nmax} (b) Random Valued Impulsive Noise with R^ £
[ nm in ' n max ]
-
III. proposed S cheme
The proposed scheme works on two stages i.e. noise detection followed by application of DAMF to the corrupted pixels only. If the center (test) pixel in a 3 x 3 window is either 0 or 255 it is considered to be noisy. If the total number of non-noisy (healthy) neighbors is greater or equals to 3 then the test pixel is replaced with median of healthy neighbors. Otherwise, the size of window in increased to 5 x 5 and the process is repeated till the window size reaches to a predefined maximum window size. The DAMF algorithmic steps are given below.
DAMF Algorithm
Input : the noisy image Y
Output: The filtered image ̂
Step 1. Initialize a sub-window size, w=3 and maximum window size,w max =15
Step 2. Select a sub-window of size w×w with center pixel as Хц .
Step 3. If Хц ∉ {0,255}, shift the window and go to
Step 1 (noise free pixel).
Step 4. Collect the set of pixels ( s ) from the subwindow ignoring the pixel with 0 or 255.
Step 5. If the size of s ≥3,
-
(i) Replace X[j with median of pixels in S .
-
(ii) Shift the window
-
(iii) Go to Step 1
Step 6. Set w= +2
Step 7. If w≤ ^max , go to Step 2.
Else replace the center pixel by mean of the pixels in sub-window of size W .
Step 8. Repeat Step 2 through Step 7 for all pixels in the image.
-
IV. SIMULATION RESULTS AND DISCUSSION
To validate the efficacy of the proposed DAMF scheme, simulation has been carried out on standard images like Lena, Boat etc. in MATLAB. The images are subjected to as low as 10% to as high as 90% noise densities. The proposed scheme along with the well performing schemes like SMF, AMF, PSMF, EDBA, IDBA, REBF, MDBUTMF are applied to the noisy images. The window size is made variable for SMF at various noise densities [12]. Subjective as well as objective evaluations have been made for each restored images. The quantitative measures used are defined below in sequel.
-
A. Peak Signal to Noise Ratio (PSNR)
/?552\
PSNR ( dB)=10Z°5io . ^/(2)
where, Mean Square Error (MSE) for an M × N is defined as,
MSB = ×N∑ ^Q1 ∑ ^( Xi ,j– ̂ ,j)2(3)
-
B. Improvement Signal to Noise Ratio (ISNR) [5]
ISNR=10 ^Sio ∑ ^[S5 ] J(4)
∑ ij [ xij x ij ]
where, image ^H , ¥ц and ̂ are the original, degraded and the restored images respectively.
-
C. Image Quality Index (IQI)
This subjective measure image quality index (IQI) models any distortion as a combination of three different factors: loss of correlation (Corr), luminance distortion (Lum), and contrast distortion (Cont) are defined as [11, 12],
IQI) = ( xw , ̂ )∗ Lum ( Xw , ̂ )∗ Cont ( Xw , ̂ ) (5)
where,
Corr ( Xw , ̂ )= Ox ̂ ⁄ 0x0 ̂
Lum ( Xw , ̂ )=2 BxB ̂ ⁄( Bx + В ̂)
Cont ( X , ̂ )=2 oxo ̂ ⁄( Ox + о ̂ )
1Q1 is first applied to local regions using a sliding window approach with size w×w . The
̂ represents the sliding window of original and restored images respectively. The statistical parameters l^x , ax and в̂, a ̂ are mean and standard deviation of the ̂ respectively. Further, ̂ is the co-variance of ̂ . Here, we have chosen w=8. At the jth step, the local quality index IQIj is computed within the sliding window using the formula given above. If there are total of M steps, then the overall image quality index is given by,
IQI =(1⁄ м )∑ ,iQh i =1,…, м (6)
The dynamic range of IQI lies in the range of -1 to 1. The best value 1 is achieved if and only if restored image ̂ is equal to the original image X .
TABLE.1 MAXIMUM WINDOW SIZE REACHED AND COMPUTATIONAL TIME FOR LENA IMAGE
|
Sl.No |
Noise(%) |
Max. Window Size Reached |
Time (Seconds) |
|
1 |
10 |
5 |
3.126634 |
|
2 |
20 |
5 |
5.501724 |
|
3 |
30 |
5 |
7.943310 |
|
4 |
40 |
5 |
10.395213 |
|
5 |
50 |
7 |
13.411614 |
|
6 |
60 |
7 |
18.423908 |
|
7 |
70 |
9 |
26.459575 |
|
8 |
80 |
13 |
40.473902 |
|
9 |
90 |
15 |
80.749149 |
TABLE.2 MAXIMUM WINDOW SIZE REACHED AND COMPUTATIONAL TIME FOR BRIDGE IMAGE
Table.3 shows the superiority of proposed method over the recently proposed MDBUTMF method for moderate and high density noises. It can be observed from the result that due to use of fixed 3x3 window size in MDBUTMF method, the occurrence of mean operation also increases with increase in noise density, whereas the proposed method DAMF which uses an adaptive process of selecting the desired window size dynamically avoids the participation of unwanted pixels, i.e. 0 and 255 in filtering operation
Tables 4, 5 and 6 depict the comparative analysis of PSNR, ISNR and IQI measures in Lena image at various
TABLE.3 COMPARISON OF MDBUTMF AND PROPOSED DAMF TECHNIQUES
|
Sl. No. |
Noise Density (%) |
Number of times mean operation is made (filtering window contains only noisy pixel values i.e 0 and 255) for Lena Image. |
|
|
MDBUTMF |
DAMF |
||
|
1 |
40 |
80 |
0 |
|
2 |
45 |
212 |
0 |
|
3 |
50 |
571 |
0 |
|
4 |
55 |
1194 |
0 |
|
5 |
60 |
2740 |
0 |
|
6 |
65 |
5362 |
0 |
|
7 |
70 |
10812 |
0 |
|
8 |
75 |
19990 |
0 |
|
9 |
80 |
35140 |
0 |
|
10 |
85 |
61287 |
0 |
|
11 |
90 |
101509 |
0 |
TABLE 4: COMPARATIVE ANALYSIS OF PSNR FOR VARIOUS FILTERS IN LENA IMAGE
|
% of Noise |
SMF |
AMF |
PSMF |
EDBA |
IDBA |
REBF |
MDBU TMF |
DAMF |
|
10 |
34.23 |
38.76 |
37.01 |
39.26 |
39.59 |
39.93 |
44.32 |
44.47 |
|
20 |
29.61 |
35.01 |
33.45 |
36.61 |
36.92 |
38.49 |
40.30 |
40.30 |
|
30 |
28.33 |
32.26 |
30.86 |
34.00 |
34.61 |
36.97 |
37.80 |
37.99 |
|
40 |
26.98 |
30.09 |
27.56 |
32.27 |
32.74 |
35.51 |
35.69 |
35.95 |
|
50 |
24.62 |
28.49 |
26.35 |
29.80 |
30.91 |
33.97 |
32.81 |
34.42 |
|
60 |
22.60 |
26.61 |
24.55 |
28.53 |
29.38 |
32.43 |
29.17 |
33.04 |
|
70 |
21.16 |
25.25 |
23.04 |
26.36 |
27.99 |
30.75 |
24.54 |
31.13 |
|
80 |
18.84 |
23.33 |
20.23 |
23.82 |
25.89 |
28.92 |
20.02 |
28.71 |
|
90 |
15.42 |
20.71 |
15.90 |
20.15 |
22.80 |
25.21 |
15.63 |
26.43 |
TABLE 5: COMPARATIVE ANALYSIS OF ISNR FOR VARIOUS FILTERS IN LENA IMAGE
|
% of Noise |
SMF |
AMF |
PSMF |
EDBA |
IDBA |
REBF |
MDBU TMF |
DAMF |
|
10 |
18.87 |
23.41 |
21.64 |
23.88 |
24.24 |
24.62 |
28.95 |
29.13 |
|
20 |
17.23 |
22.61 |
21.12 |
24.28 |
24.52 |
26.16 |
27.99 |
27.96 |
|
30 |
17.59 |
21.69 |
20.25 |
23.29 |
23.97 |
26.41 |
27.21 |
27.38 |
|
40 |
17.14 |
20.75 |
18.24 |
22.90 |
23.41 |
26.17 |
26.34 |
26.60 |
|
50 |
16.16 |
20.10 |
17.97 |
22.02 |
22.53 |
25.60 |
24.44 |
25.87 |
|
60 |
15.02 |
19.02 |
16.98 |
20.96 |
21.97 |
24.84 |
21.58 |
24.74 |
|
70 |
14.25 |
18.34 |
16.13 |
19.46 |
21.08 |
23.82 |
17.64 |
24.19 |
|
80 |
12.51 |
16.99 |
13.91 |
17.49 |
19.56 |
22.59 |
13.69 |
22.37 |
|
90 |
9.61 |
14.89 |
9.91 |
14.34 |
16.99 |
19.53 |
9.80 |
20.61 |
TABLE 6: COMPARATIVE ANALYSIS OF IQI FOR VARIOUS FILTERS IN LENA IMAGE
|
% of Noise |
SMF |
AMF |
PSMF |
EDBA |
IDBA |
REBF |
MDBU TMF |
DAMF |
|
10 |
0.8759 |
0.9404 |
0.9670 |
0.9336 |
0.9359 |
0.9375 |
0.9740 |
0.9737 |
|
20 |
0.7335 |
0.9268 |
0.9477 |
0.9235 |
0.9253 |
0.9330 |
0.9609 |
0.9593 |
|
30 |
0.7147 |
0.9028 |
0.9230 |
0.9019 |
0.9040 |
0.9237 |
0.9437 |
0.9418 |
|
40 |
0.6839 |
0.8714 |
0.8934 |
0.8700 |
0.8743 |
0.9084 |
0.9182 |
0.9218 |
|
50 |
0.5800 |
0.8301 |
0.8615 |
0.8230 |
0.8337 |
0.8852 |
0.8600 |
0.8945 |
|
60 |
0.5211 |
0.7745 |
0.8107 |
0.7657 |
0.7918 |
0.8514 |
0.7309 |
0.8519 |
|
70 |
0.4131 |
0.6970 |
0.7580 |
0.6778 |
0.7327 |
0.8014 |
0.4945 |
0.8223 |
|
80 |
0.2773 |
0.5897 |
0.6509 |
0.5469 |
0.6369 |
0.7224 |
0.2634 |
0.7148 |
|
90 |
0.1444 |
0.4041 |
0.4362 |
0.3162 |
0.4438 |
0.5033 |
0.1058 |
0.6351 |
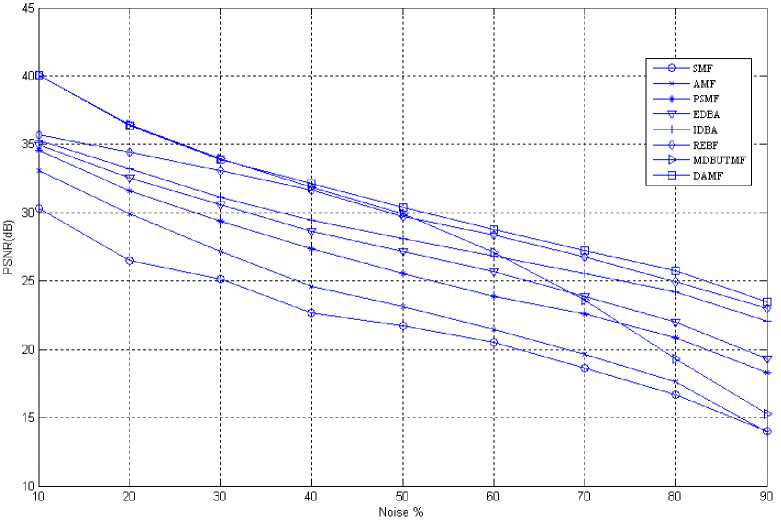
Figure 2: PSNR characteristics for Boat image at various noise densities

Lena image

Noisy Image


AMF


DBA

IDBA
SMF

REBF
(a) 70% Noise case

MDBUTMF
PSMF

DAMF

Lena image

Noisy Image

SMF

AMF

PSMF

DBA

IDBA

REBF
(b) 90% Noise case

MDBUTMF

DAMF
Figure 3: Restored Lena images of various filters for image corrupted with (a) 70% noise (b) 90% noise
V. C onclusion
In this paper, we propose a dynamic adaptive filtering scheme, namely, DAMF to recover images corrupted with high density salt and pepper noise. The filter works in two phases, namely, identification of corrupted locations followed by the filtering operation. The window size for any test pixel is selected dynamically utilizing the local information from its neighbors. Subsequently, it applies the median filter considering only the window of the non-corrupted neighbors. The proposed scheme is evaluated both qualitatively as well as quantitatively. The comparative performance analysis in general shows that the proposed scheme outperforms the existing schemes both in terms of noise reduction and retention of images details at high densities (> 40%) impulse noise.
Restored Images Image Quality Map of Restored Images
(a) 30% (b) 60% (c) 90% (a) 30% (b) 60% (c) 90%

Figure 4: Column a, b and c represent the restored images of Lena image corrupted with 30%, 60% and 90% noise respectively. Column d, e and f represent the corresponding image quality map. Rows 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10 represents the restored images after applying the SMF, PSMF, AMF, MMEM, DBA, IDBA, REBF, NIMF, MDBUTMF and the proposed DAMF filters respectively.
(b) 30%

Restored Images
(b) 60%

(c) 90%



Image Quality Map of Restored Images
(b) 30%
(b) 60%
(c) 90%

Figure 5: Column a, b and c represent the restored images of Boat image corrupted with 30%, 60% and 90% noise respectively. Column d, e and f represent the corresponding image quality map. Rows 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10 represents the restored images after applying the SMF, PSMF, amf, mmem, dba, idba, rebf, nimf, mdbutmf and the proposed damf filters respectively .



Список литературы Dynamic Adaptive Median Filter (DAMF) for Removal of High Density Impulse Noise
- I.A. Pitas and A.N. Venetsanopolous, “Nonlinear digital filters principles and applications”, Kluwer Press, Dordrecht, 1990.
- Zhou Wang and David Zhang, “Progressive Switching Median Filter for the Removal of Impulse Noise from Highly Corrupted Images” IEEE Transactions On Circuits And Systems—II: Analog And Digital Signal Processing, vol. 46, no. 1, pp.78-80, January 1999.
- Hwang, H. and Haddad, R.A., “Adaptive median filters: new algorithms and results”, IEEE Trans. Image Processing, vol. 4, no.4, pp.499–502, 1995.
- Wei-Yu Han and Ja-Chen Lin, “Minimum-maximum exclusive mean (MMEM) filter to remove impulse noise from highly corrupted images”, Electronics Letters, vol. 33, no. 2, 16th January, 1997.
- C. Wang, T. Chen, and Z.Qu, “A Novel Improved Median Filter for Salt-and-Pepper Noise from Highly Corrupted Images”, 3rd International Symposium on Systems and Control in Aeronautics and Astronautics (ISSCAA 2010), Harbin, China, pp.718-722, IEEE, 8-10 June,2010.
- Eng, H.-L., Ma, K.-K.“Noise adaptive soft-switching median filter”, IEEE Trans. Image Processing, vol. 10, no.2, pp.242–251, 2001.
- Srinivasan, K.S., Ebenezer, D., “A new fast and efficient decision based algorithm for removal of high-density impulse noises”, IEEE Signal Processing Letters, vol. 14, no. 3, pp.189–192, 2007
- Madhu, N.S., Revathy, K., Tatavarti, R., “An Improved Decision Based Algorithm for Impulse Noise Removal”, In: Proceedings of 2008 International Congress on Image and Signal Processing— CISP 2008, pp. 426–431. IEEE Computer Society Press, Sanya, Hainan, China 1, 2008.
- V.R.Vijaykumar, P.T.Vanathi, P.Kanagasabapathy and D.Ebenezer,“High Density Impulse Noise Removal Using Robust Estimation Based Filter”, IAENG International Journal of Computer Science, vol.35, issue.3,IJCS_35_3_02, 2008.
- S.Esakkirajanet. al., “Removal of high density Salt and pepper noise through modified decision based unsymmetric trimmed median filter”, IEEE signal processing letters, vol. 18(5), pp. 287-290, May, 2011.
- Zhou Wang, Alan C. Bovik, “A Universal Image Quality Index”, IEEE Signal Processing Letters, vol. XX, no. Y, March 2002.
- Madhu S. Nair and G. Raju, “A new fuzzy-based decision algorithm for high-density impulse noise removal”, Journal of Signal, Image and Video Processing, Springer, in press, DOI 10.1007 / s11760 – 010 - 0186-4.


