Dynamic Characteristics of the Hippocampal Neuron under Conductance’s Changing

Published Online February 2011 in MECS

In the 1990s, neuron modeling in hippocampal region

The corresponding author is Yueping Peng.

has been becoming the research hotspot in the field of neural science. Depended on electrophysiological experiments and new technologies such as optics imaging, some models of hippocampal pyramidal Neuron based on ionic conductance have been successfully constructed; The work of R.D.Traub’s research team is the most excellent [1-20]. In 1991, based on the electrophysiological experiment data of Guinea pig hippocampal neurons, R.D.Traub had developed a 19-compartment cable model of CA3 pyramidal neuron; Based on the model, R.D.Traub’s research team had deeply studied these issues such as hippocampal neuronal network, EEG rhythm, plasticity of hippocampal neuron Synapse, electrical coupling influence on hippocampal neuron’s high frequency oscillation, and cortical neuron’s rapid oscillation[8-10]. Based on R.D.Traub research team’s returns and the electrophysiological experiment data, Warman had developed a 16-compartment cable model of CA1 pyramidal neuron based on ionic conductance by computer simulation, and had successfully simulated electrophysiological features and experimental results of CA1 pyramid neuron[11].

The hippocampal CA1 pyramid neuron has plenty of discharge actions. Yue found that bursting behavior persists in adult CA1 pyramidal cells after almost complete truncation of the apical dendrites. The mechanism of bursting is different from the “ping-pong” mechanism, which depends on the integrity of apical dendrites[12-14]. Based on the CA1 pyramidal neuron’s membrane ionic channel theory and its electrophysiological experimental data, according to the basic frame of H-H class model, David had developed one-compartment model of CA1 Pyramidal Neuron by neurodynamic theory[15]. The model is different from former multi-compartment cable models of the hippocampal pyramid neuron. This model omits the effects of the apical dendrites and the complexity is reduced, which not only can simulate many electrophysiological features and experimental results of the hippocampal CA1 pyramid neuron, but also can spontaneously generate regular firing, tonic firing, rhythmic bursting, and so on.

In this study, we take the nine-dimension one-compartment complex model of CA1 pyramid neuron developed by David as the object, and analyze and discuss the model’s dynamic characteristics by the neurodynamic theory[21-25] and methods.

dq ₌ q ∞ ([ Ca ^{2 +} ] i ) - q _;

dt          τ _q

^{d [ Ca 2 + ]} i =- υ g Ca r ²( V - V Ca ) - ^{[ Ca 2 + ]} i ;           (1)

dt                               τ _Ca

II. The Nine-Dimension Model of CA1 Pyramid Neuron and Its Discharge Patterns

The nine-dimension one-compartment model of CA1 pyramid neuron developed by David has multiple time scale dynamic action. The current balance equation of the model is as follows:

C ^dV = - I L dt

I Na ^- I NaP

- I_Kdr - I_A

I_M - I_Ca

I Y ^- I sAHP ⁺ I App

Where C is the

membrane capacitance; V is the

membrane potential; I L is the leakage current; I Na is the transient Na⁺ current; I NaP is the persistent Na⁺ current; I Kdr is the delay rectification K⁺ current; I A is the A-type instantaneous K⁺ current; I M is the muscarine-sensitive K⁺ current; I_Ca is the high-threshold Ca²⁺ current; I_y is the fast Ca²⁺-activated K⁺ current; I_SAHP is the slow Ca²⁺-activated K⁺ current; I APP is the stimulation current.

Currents of above balance equation are changed into their corresponding ionic conductance forms, and the eight corresponding time variables are also added. Therefore, the models are changed into set of nine-dimension ordinary differential equations,

The equation model has nine time variables: the membrane potential variable V, transient Na+ current inactivation variable h, delayed rectified K+ current activation variables n, A-type instantaneous K+ current inactivation variables b, muscarine-Sensitive K+ current-activated variables Z, high-threshold Ca2+ current-activated variable r, fast Ca2+-activated K+ current-activated variable y, slow Ca2+-activated K+ current-activated variable q, and intramembrane calcium ion concentration variable [Ca2+]i. At numerical calculation, the values of model parameters refer to appendix A. In addition, the state variable of the model is (V, h, n, b, z, r, y, q, [Ca2+]i), and the initial state of the model is (-65, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.05).

The nine-dimension model of CA1 pyramid neuron showed by formula (1) can spontaneously generate regular firing, tonic firing, rhythmic bursting, and so on[15]. Based on MATLAB simulation methods, several common discharge patterns of the nine-dimension model of CA1 pyramid neuron under different currents’ stimulation are showed in Figure 1.

C dV dt

- g L ( V - V L ) - g Na m ∞ ³( V ) h ( V - V Na )

- g NaP p ∞ ( V )( V - V Na ) - g Kdr n ⁴( V - V K )

- g A a ∞ ³( V ) b ( V - V K ) - g M z ( V - V K )

-

g Ca r ²( V - V Ca ) - g y d ∞ ([ Ca ^{2 +} ] i ) y ( V - V K )

- g_sAHPq ( V - V_K ) + I_App ;

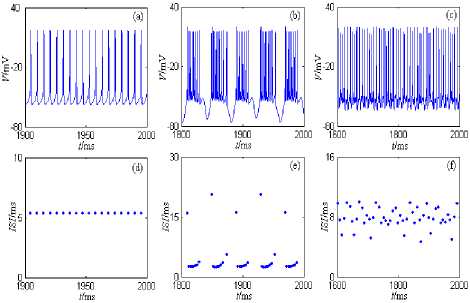
Figure 1. Discharge patterns of the nine-dimension model of CA1 pyramid neuron. (a) and (d) are the period 1 discharge pattern. (b) and (e) are the bursting discharge pattern. (c) and (f) are the chaos discharge pattern.

dh dt

h ∞ ( V ) - h ; τ h ( V )

dn  n _∞ ( V ) - n ;

dt ⁼ τ n ( V )

db ₌ b ∞ ( V ) - b ; dt       τ _b

dz   z _∞ ( V ) - z

= ^;

dt       τ _z

dr  r _∞ ( V ) - r

= ^;

dt       τ _r

dy y _∞ ( V ) - y = ^;

dt      τ _y

III. STUDY ON DYNAMIC CHARACTERISTICS OF THE CA1 Pyramid Neuron Model

The hippocampal CA1 pyramid neuron has plenty of discharge actions. The nine-dimension model’s dynamic characteristics are discussed in the following, and at numerical calculation the values of model’s parameters are showed in appendix A.

There are all kinds of voltage or ligand gating ionic channels such as potassium channel, calcium channel, sodium channel in the membrane of hippocampal pyramid neuron. The transient Na⁺ current( I _Na ) and the delay rectification K⁺ current( I _Kdr ) widely exist in all kinds of neurons, which also pay an important role in the

discharge process of the neuron model described by formula (1). In the following, the dynamic characteristics of the neuron model described by formula (1) are discussed when the maximum conductance’s of the transient Na+ current and the delay rectification K+ current are changed.

A.    Dynamic Characteristics undergNa ’s Changing

The stimulation current is 10nA. The range of g _Na (the maximum conductance of the transient sodium channel) is 0~100 mS/cm² ， and the changing step is 0.1mS/cm². The simulation time is 0~2000ms, and ISI’s graphing time interval is 1000~2000ms. Fig.2 shows the ISI bifurcation figure of the neuron model under g _Na ’s Changing.

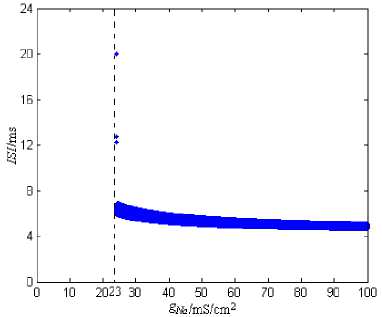
Figure 2. The ISI bifurcation figure of the neuron model under g _Na ’s

Changing.

From Fig.2, for the neuron model described by formula (1), it can generate the discharge process only when g _Na (the maximum conductance’s of the transient sodium channel) reaches a certain threshold (about 23mS/cm²). So in the discharge’s formation process of the model, g _Na is indispensable. But g _Na ’s changing affects little in the discharge process of the neuron model, and the ISIs approximate to a straight line; That is to say, the discharge frequency keeps unchanged.

B.    Dynamic Characteristics undergKdr ’s Changing

The stimulation current is 10nA. The range of g _Kdr (the maximum conductance of the delay rectification potassium channel) is 0~20mS/cm² ， and the changing step is 0.05mS/cm². The simulation time is 0~2000ms, and ISI’s graphing time interval is 1000~2000ms. Fig.3 shows the ISI bifurcation figure of the neuron model under g _Kdr ’s Changing.

From Fig.3, for the neuron model described by formula (1), it can generate the discharge process when gKdr (the maximum conductance’s of the transient potassium channel) is 0mS/cm2. So in the discharge’s formation process of the model, gKdr isn’t indispensable. But gKdr ’s changing affects much in the discharge process of the neuron model. When gKdr is less than 3.2mS/cm2, the neuron model has plenty of discharge patterns; When gKdr is near 1mS/cm2, 1.6mS/cm2, 2.5mS/cm2, and 2.8mS/cm2, the neuron model’s discharge pattern is the chaos, but in other region of gKdr , the neuron model’s discharge pattern is mainly the period. In addition, the range of ISIs is about 3~50ms, and the discharge frequency is wide. When gKdr is near 2.9mS/cm2, the neuron’s discharge pattern evolves from the chaos to period 2; with gKdr ’s increasing gradually, the neuron’s discharge pattern evolves into period 1 near 3.2 mS/cm2 via the adverse adding period bifurcation. When gKdr is more than 3.2mS/cm2, the neuron’s discharge pattern is period 1, and the ISIs approximate to a straight line; That is to say, the discharge frequency keeps unchanged.

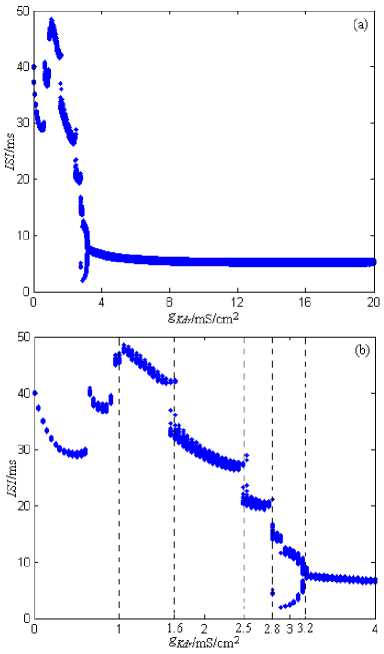
Figure 3. The ISI bifurcation figure of the neuron model under g _Kdr ’s Changing. (a) g _Kdr is 0~20 mS/cm². (b) g _Kdr is 0~4 mS/cm².

Fig.4 shows the neuron model’s attractors on V-n phase plane under g _Kdr ’s changing, where the stimulation current is 10nA. The simulation time is 0~2000ms, and the graphing time interval is 1000~2000ms.

From Fig.4, When g _Kdr is 0mS/cm², 1mS/cm², 1.55mS/cm², 2.8mS/cm², and 3.2mS/cm², the neuron model’s orbits in the phase plane all form the limit cycle, and generate the discharge process, whose discharge patterns are mainly period 1 or the chaos. So g _Kdr ’s changing can make the neuron model to generate many discharge patterns, and have an important impact on the discharge characteristics.

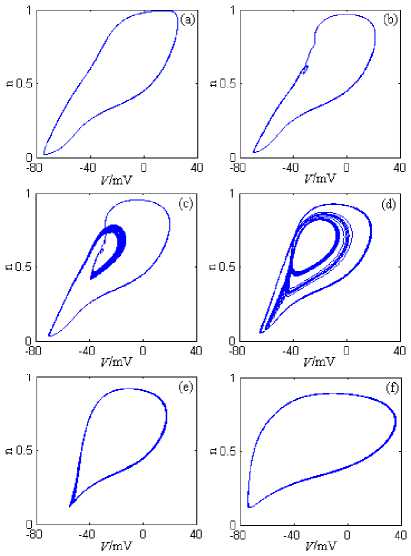
Figure 4. The neuron model’s attractors on V-n phase plane under g_Kdr ’s changing. (a) g_Kdr =0mS/cm². (b) g_Kdr =1mS/cm². (c) g_Kdr =1.55mS/cm². (d) g_Kdr =2.8mS/cm². (e) g_Kdr =3.2mS/cm². (f) g_Kdr =5mS/cm².

The neuron model has plenty of discharge patterns under g _Kdr ’s changing. From the angle of neuro dynamics, the neuron model changes from a discharge pattern to another discharge pattern, and in this process the neuron model substantially undergoes the dynamic bifurcation. In order to describe the dynamic bifurcation process clearly, Fig.5 and Fig.6 respectively shows the neuron model’s phase plane attractor bifurcation chart when g _Kdr is near 1.6mS/cm² and near 3mS/cm², where the stimulation current is 10nA. The simulation time is 0~2000ms, and the graphing time interval is 1000~2000ms.

From Fig.5, when gKdr is 1.2 mS/cm2, the neuron model’s discharge pattern is period 1; With gKdr ’s increasing gradually, the neuron model evolves into the chaos discharge pattern via the adding period bifurcation, and goes into the multiply periodic discharge pattern via the adverse adding period bifurcation; At last, the neuron model’s discharge pattern becomes period 1 via the adverse adding period bifurcation.

From Fig.5, when g_Kdr is 1.2 mS/cm², the neuron model’s discharge pattern is period 1; With g_Kdr ’s increasing gradually, the neuron model evolves into the chaos discharge pattern via the adding period bifurcation, and goes into the multiply periodic discharge pattern via the adverse adding period bifurcation; At last, the neuron model’s discharge pattern becomes period 1 via the adverse adding period bifurcation.

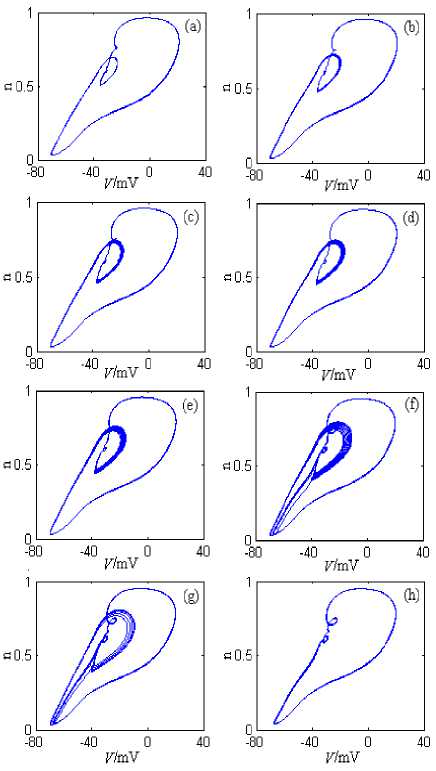
Figure 5. The neuron model’s attractors’ changing process on V-n phase plane, where g_Kdr is 1.2~1.7mS/cm². (a) g_Kdr =1.2mS/cm². (b)

g_Kdr =1.3mS/cm². (c) g_Kdr =1.4mS/cm². (d) g _Kdr =1.45mS/cm². (e) g_Kdr =1.5mS/cm². (f) g_Kdr =1.6mS/cm². (g) g_Kdr =1.65mS/cm². (h) g_Kdr =1.7mS/cm².

From Fig.6, when gKdr is 2.75 mS/cm2, the neuron model’s discharge pattern is the chaos; With gKdr ’s increasing gradually, the orbits in the chaos attractor region gradually coalesce and annihilate each other; When gKdr is near 2.85 mS/cm2, the chaos attractor becomes the limit cycle of period 2, and the neuron model goes into the period 2 discharge pattern. With gKdr ’s continually increasing, the inner limit cycle is instable and gradually closes to the outward stable limit cycle; When gKdr is near 3.15 mS/cm2, the two limit cycles fold and become a limit cycle, and the neuron model evolves from the period 2 discharge pattern to the period 1 discharge pattern via the adverse adding period bifurcation.

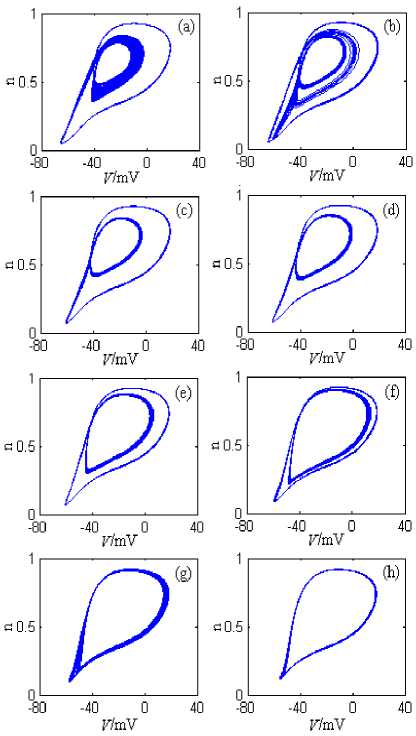
Figure 6. The neuron model’s attractors’ changing process on V-n phase plane, where g _Kdr is 2.75~3.3mS/cm². (a) g_Kdr =2.75mS/cm². (b) g_Kdr =2.8mS/cm². (c) g_Kdr =2.85mS/cm². (d) g_Kdr =2.9mS/cm². (e) g_Kdr =3.0mS/cm². (f) g_Kdr =3.1mS/cm². (g) g_Kdr =3.15mS/cm². (h) g_Kdr =3.2mS/cm².

indispensable in the discharge’s formation process of the model. The model can generate the discharge process only when g _Na reaches a certain threshold. In addition, g _Na ’s changing affects little in the discharge process of the neuron model, and the ISIs approximate to a straight line; That is to say, the discharge frequency keeps unchanged. The delay rectification K⁺ current( I _Kdr ) caused by g _Kdr isn’t indispensable in the discharge’s formation process of the model. But g _Kdr ’s changing affects much in the discharge process of the neuron model. With g _Kdr ’s changing, the neuron model undergoes different dynamic bifurcation process, and has plenty of discharge patterns, and these discharge patterns mainly include the chaos, period, and so on.

This investigation is helpful to know and investigate deeply the dynamic characteristics and the bifurcation mechanism of the hippocampal neuron; and it provides a certain theory assist to investigate the neural diseases such as the Alzheimer disease by the neurodynamics.

Appendix A

Parameters’ values of the nine-dimension one-compartment complex model of CA1 pyramid neuron developed by David are as follow:

C = 1 uF I cm ²;

g_L = 0.05 mS I cm ² ;

V_L =- 70 mV ;

g_Na = 35 mS I cm ² ;

g_NaP is about 0~0.41mS/cm²;

g_Kdr = 6 mS । cm ²;

g_A = 1.4 mS I cm ²;

g_M = 1 mS I cm ²;

Vn„ = 55 mV ;

V_K =- 90 mV ;

is about 0~0.2mS/cm2; gCa gy = 10 mS I cm2;

g sAHP = ^{5 mS I} cm ²;

V_Ca = 120 mV ;

VI. Conclusion

The hippocampal CA1 pyramid neuron has plenty of discharge actions, and can generate many discharge patterns such as period, the chaos, and so on. Under the certain amplitude current’s stimulation, the change of g _Na (the maximum conductance of the transient sodium channel) and g _Kdr (the maximum conductance of the delay rectification potassium channel) can cause different dynamic characteristics of the neuron model. The transient Na⁺ current( I _Na ) caused by g _Na is

m „ ( V ) =

1      / — 30 — V x

1 + exp(--------)

9.5

P „ ( V ) =

^, — V

1 + exp( p 3 )

— 47 mV <  9 _p <— 41 mV ;

a „ ( V ) =

;

- 50 - V

1 + exp( ⁵⁰ V )

d - ([ Ca 2 ⁺ ] , ) = —

1 +

;

h , ( V ) =-------

1 + exp(

[ Ca ²⁺ ] , 1

- 45 - V

- 7

;

)

T h (V ) = 0.1 + 0.75 x--------

1 + exp(

-

n , (V ) =-------

1 + exp(

- 35 - V

;

)

- 27 - V

T n (V ) = 0.1 + 0.5 x--------

1 + exp(

40.5 - V

;

- 6

)

- 15

;

)

b „ ( V ) =--------

1 + exp(

1 _;

- 80 - V

- 6 )

T b = 15 ms ;

2 „ ( V ) =-------

1 + exp(

- 39 - V

;

)

t _ = 75 ms ;

1 _;

" ⁽ ) ,        - 20 - V_x

1 + exp(--------)

T r = 1 ms ;

У „ ( V ) =-------

1 + exp(

- 30 - V

;

)

T y = 2 ms ;

t = 450 ms ;

q и = 0.13cm2 /(ms x цА);

q - ([ Ca ^{2 +} ] , ) = —

1 +

;

[ Ca 2 ⁺ ] 4

^T Ca = ¹³ ms

Acknowledgment

The authors would like to thank “The 2nd International Conference on Biomedical Engineering and Computer Science (ICBECS 2011)” for providing the chance and really appreciate the anonymous reviewers for the valuable comments on the paper.