Dynamic Effort Allocation Problem Using Genetic Algorithm Approach

Software development phase is complex but it is a major part of any Software Development Life Cycle (SDLC). The challenge will become harder when the process of development is considered in the dynamic environment. To decrease uncertainty in the process, companies often set up different kind of project/software management tools to coordinate with the other modules of the software project. Software will be released to the customers after the testing phase of SDLC. With superior development and testing efforts, superior quality software can be guaranteed. But this may be very time consuming and is unattractive in the dominant modest market conditions. Distribution of financial efforts to a software development project through the testing phase in the dynamic environment will be a critical decision that a software manager has to take. Throughout testing resources such as human effort and computer time are consumed. The error detection and removal process will completely depend upon the behavior and quantity of resources used. Several software reliability growth models (SRGMs) are proposed in the last 10 years to discuss the minimization issue of the testing effort expenditures [1], [2]. Often these models are based on the assumption that the testing effort consumption and testing time follow Rayleigh and exponential distribution. The time dependent performance of the testing effort has been studied by many authors [3-6].

Earlier studies explored that exponential curve can be used if the software testing resources are equally consumed with respect to the testing time otherwise Rayleigh curve. Weibull-type and Logistic functions will also be used to define the testing effort. Another school of thought assumes that the resource consumption can be expressed as an explicit function of the total number of faults deleted and calendar time consumed [7]. More recently, [8] have given a SRGM based on stochastic differential equations in order to study the active position of the open source development assuming that the intensity of software failure fully depends on the time, and the software fault exposure occurrence on the bug tracking system retain an unbalanced state. As discussed, over the last three decades many SRGMs have been proposed to minimize the total testing effort expenditures, but mostly under static environment. However in this paper we have tried to study an optimal resource allocation plan to optimize the testing cost of software throughout the testing phase under dynamic situation. This paper also explores the optimal resource allocation problems for various conditions by examining the behavior of the model parameters and also proposes the related release policy.

The paper uses genetic algorithm (GA) approach to discuss dynamic allocation problem. Optimal control theory is used for problem formulation and analysis of the model properties. The proposed approach is helpful to solve the dynamic nature of the problem which is difficult to solve with ordinary optimization technique.

The paper is subdivided into seven sections. Section two describes the research background related to testing effort allocation and release time problem. Section three describe about the model and its solution. We use optimal control theory and genetic algorithm for solving problem. Section four describes about basic parameter for genetic algorithm. Section five solves a numerical problem for testing effort allocation using genetic algorithm. Section six describe about optimal release policy for introducing software product in market for solving this problem we use genetic algorithm. Finally in section seven we conclude our results and findings.

Nomenclature

a	is the initial fault content in the software.
b	is the fault detection rate.
f(t)	is the number of fault removed at time ‘t’.
m(t)	is the cumulative number of fault detected till time ‘t’ due to the testing effort w 1 (t).
T	the planning period.
C 1 (m(t),w 2 (t)) Cost per unit at time ‘t’ for cumulative faults removed m(t) and debugging effort w2(t).
C 2	is the cost of testing per unit testing efforts.
W	is the total resources utilized during the SDLC at any point of time ‘t’.

• II.    Research Background

Software reliability growth model (SRGM) provides a measure to estimate upcoming failure behavior from identified or presumed features of the software. Numerous SRGMs have been given in software reliability field under some set of conventions and testing environment. The proposed SRGM in this article takes into account that the time is dependent upon variation in the testing effort. The testing efforts that direct the pace of testing for almost all kind of software projects are [7]:

• (a)    Manpower which contains:

• •     Failure detection professionals.

• •     Failure rectification professionals.

• (b)    Computer time.

The vital role of person engaged in testing is to execute test cases and match the test results with preferred specifications. Upon a failure, the error affecting it is identified and then removed by failure rectification personnel. The influence of testing effort has been included in few SRGMs [8-15]. In 1976, Myers planned that software system should be constructed and tested separately in a sequential step. [6], [5] and [16] have recommended that system level testing happened only after the system was fully developed. Recently, [17], however, suggested that software development, system debugging and software testing should be considered as simultaneous activities. [14] Investigated the association between the number of faults deleted with respect to testing effort and/or time. The authors proposed that throughout the testing phase of an SDLC, faults are removed in two stages. First a failure happens and then the fault causing that failure is corrected; hence the testing effort should be spent on two separate processes; failure detection and failure rectification. In their paper, the authors developed an SRGM incorporating time delay not only between the two phases but also through the segregation of resources between them and proposed two alternate methods for controlling the testing effort for achieving the preferred reliability or error detection level. [18] Discussed a development process environment in which system integration will take place when the total number of errors in the software will achieve a definite threshold. [19-20] studied software release policies to minimize total development cost while achieve a definite reliability objective in dynamic environment. [21] Have proposed optimal release policy for module based software.

• III.    Model Formulation And Solution

We initiate our study by defining a common model with a very little assumption. We are limiting our analysis to the case of a firm that controls its resources for testing and debugging under limited planning horizon. We are also consistent with the plan that the hidden faults in the software are exposed and removed throughout the testing phase, and the total number of faults residual in the software slowly decreases as the testing progresses. Hence, it is rational to assume the following differential equation:

f(t) = ^—m ( t ) = bw j( t )[ a - m ( t )]    (1)

dt                 ¹

Now, suppose the software firm wants to minimize the overall expenditure over the fixed scheduling horizon T. Then, the objective function for the company will be specified by;

T

Min ^[ c 1 ⁽ t ) f ⁽ t ) + c 2 w 1 ⁽ t ^{)] dt} 0

Subject to

^f(t) = d-m ⁽ t ) = f ⁽ b , w 1 ⁽ t ))       ⁽²⁾

dt

m ( t )

-----> m T >  m ( T ) >  m _d ( = am _T ) a

Where

m(0)=0 and w 1 (t)+w 2 (t)=W

(w 1 (t); w 2 (t))≥0 and c 1 (t) =c 1 (m(t),w 2 (t)).

Here, in the above optimal problem 0T<1, we have considered the desired reliability level to be at least ma (where ma is unique). The planning period is [0,T] and the assumption m(T)≥md means that the firm aims at reaching at least the level ma at the end of the planning period. The planning problem is to find the allocation of resources that minimizes the total expenditure.

To solve the above optimization problem, let w1*(t) be an admissible control vector which transfers (m0,t0) to a target (m(T),T), where final state m(T) is specified but the final time T is not specified. t0 and m0 are the initial time and state, and are both fixed, i.e. (t0,m(0)=(0,m0)). Assuming that m*(t) is corresponding to w1*(t), then by Pontryagin Maximum principle, in order for w1*(t) to be optimal, it is essential that there exists a non-zero, continuous vector function λ*(t) and a constant scalar λ0

such that [22]:

• (a)    λ^*(t) and m*(t) are the explanation of the canonical system

∂m*(t)

=       ( m , λ , w , t )

∂t       ∂λ

∂ λ* (t)       ∂ H      *    **

= -        ( m , λ , w ₁, t )

∂ t ∂ m

Where the current value of Hamiltonian function with λ 0

=1 must initially be defined, that is

H(m(t),w 1 (t),λ(t),t)=

- [ c 1 ( t ) f ( t ) + c 2 w 1 ( t )] + λ ( t ) f ( t ) = ₃

[ - c 1 ( t ) + λ ( t )] f ( t ) - c 2 w 1 ( t )              ⁽

• (b)    H ( m ^*, λ ^* , w ₁^*, t ) ≥ H ( m ^*, λ , w ₁ , t ) (c) All boundary conditions be satisfied.

W 1 ^*(t) maximizes

[ - c ₁( t ) + λ ( t )] f ( t ) - c ₂ w ₁( t ) ∀ w ₁( t )

(

≥ 0

We can interpret λ(t) as the marginal value of faults at time ‘t’, which will be negative because increasing the number of faults will increase the debugging charge. The physical explanation of the Hamiltonian H can be given as follows:

λ(t) stands for future cost incurred as one more fault is introduced in the system (at time t). Thus the Hamiltonian is the sum of testing cost c 2 w 1 (t), current cost c 1 (t)f(t) and future cost λ(t)f(t). Here, H denotes the instantaneous entire cost of the firm at time t.

The followings are two necessary conditions that hold for an optimal solution:

= 0 ⇒ - ( c ₁ - λ ) fw ₁ - c ₁ w ₁ f - c ₂ ∂ w ₁

= 0

Other optimality condition is

From the above optimality conditions, we will get the following results:

⇒ w ₁^* ( t ) =

( λ ( t ) - c ₁( t )) b ( a - m ( t )) - c ₂      (5)

c _{1 w 1( t )} ( t ) b ( a - m ( t ))

And, w 2* (t) = w - w 1* (t)

The value of m (t + Δt) = m (t) + Δt[bw 1 (a - m (t))]

And,

λ ( t + Δ t ) = λ ( t ) + Δ t [ - bw ₁( t )

( c 1 - λ ( t ))]                                     ⁽⁷⁾

The corresponding Hamiltonian will be given as

H(t)=

( - c ₁ ( t ) + λ ( t )) bw ₁ ( t )( a

- c ₂ w ₁( t )

- m ( t ))

And the adjoint variable λ(t) can be defined as d λ(t) = λ*(t) = -bw1(t)(c1 - λ(t))] dt

With the transversality condition at t=T^*, H(T^*)= 0 and λ(T^*)≤0 (=0 if m^*(T^*)>m a )

From (9) and the transversality condition of λ(T) we have

T

λ ( t ) = λ ( T ) + bw ( t )( c - λ ( t )) dt

The necessary condition for optimality is H w1 =0

Now,

∂ ² H ∂ w ₁ ²

≤ 0 ⇒

- ( c ₁

-

λ ) f w 1 w 1

-

c

1 w 1 w 1

f

- 2 c 1 w 1 f w 1 ≤ 0

H _{w 1} = ( - c ₁ + λ ) xw ₁ - c ₂ = ( λ - c ₁ ) b ( a - m ) - c ₂

Where c 1 w 1

∂ c

¹ and c _{1 w 1 w 1} ∂ w ₁

∂ ² c ₁

∂ w ₁ ²

The above optimization problem is solved by genetic algorithm approach (GA), which is categorized as a powerful computerized exploratory search and optimization method [23-26].

GA is a popular computerized heuristic method based on the Darwin’s evolutionary theory and natural genetics. Genetic Algorithm has been effectively implemented on diverse area of optimization problem like transportation, assignment problems, inventory control, job scheduling and decision-making problems based on real-life situation. The main essential feature of Genetic Algorithm (GA) is to mimic the genetic reproduction and natural evolution procedure artificially. In this process populations undertake continuous change using some genetic operators like selection, inheritance, crossover (also called recombination), and mutation. Genetic algorithm is very beneficial for solving difficult type of problems which are very hard to solve using some other algorithmic techniques. The Genetic algorithm (GA) evolution usually begins with a population of randomly generated individuals to an assumed problem where each and every individual is described using some form of encoding (Binary encoding, permutation encoding, value encoding) as a chromosome. We used binary encoding in our problem. These chromosomes will evaluate their objective function. Based on their objective functions value, chromosomes inside the population will be chosen for reproduction and selected individuals are manipulated by crossover and mutation. Basically, the crossover is used to produce offspring from two selected chromosomes. And the mutation is use for a small alteration to breed offspring. For every new generation of solutions, there is some improvement over the previous one. This method is applied iteratively until satisfies the termination criterion.

To implement the above Genetic Algorithm for the planned model, the following standard mechanisms will be measured;

• (i)    Genetic algorithm parameters (size of population, rate of mutation and rate of crossover)

• (ii)    Representation of chromosome

• (iii)    Population initialization

• (iv)    Evaluation of objective function

• (v)    Selection process

• (vi)    GA operators (Crossover, Mutation and elitism)

• IV.    GA Parameters

Primarily, we have to decide the different parameters on which the said GA depends. All these parameters include population size (p-size), maximum number of generation (max-gen), crossover rate (p-cros) and mutation rate (p-mute). For choosing population size there is no fixed rule for GA. If the size of population is huge, keeping of records in middle steps of genetic algorithm might raise some difficulties at execution time. If the size of population is very small, few genetic operators will not work appropriately. Regarding the number of maximum generations, there is no fixed sign to consider this value. From the natural genetics it is clear that the crossover rate is always greater than mutation rate. Generally, the crossover rate lies between 0.5 and 0.95 whereas mutation rate lies between 0.06 and 0.02.

Chromosome representation Genetic Algorithm always starts with the initial population of solutions represented as chromosomes. A chromosome comprises of genes where each gene represents a specific feature of the solution.

Initial population for a specified total testing effort W and for fault detected at time t, GA produces the initial population randomly. It will initialize random values within the bounds of every variable. The main role of the population is to hold likely solutions.

Selection In genetic algorithm selection operator plays vital role because selection is the very first operator applied to the population. The main goal of this operator is to choose the above average chromosome based on the fitness value of every chromosome and remove lower average chromosome from the population for the subsequent generation under the principle “survival of the relatively fit”. In this Experiment, we have used tournament selection.

However, to solve the problem dynamically, the initial value of λ(0) and f(0) must be given first then, from objective function we will find the optimal value of effort and fault detected at time t.

Table 1. Parameters of the GA

Parameter	Value
Population Size	20
Number of Generation	100
Selection Mode	Tournament
Crossover Probability	0.8
Mutation Probability	0.2

Based on the above parameters problem is solved using MATLAB (gatool) version 7.4.0 Global Optimization Toolbox User’s Guide [27].

• V.    Numerical analysis

  Assume that

  
  

  a=100, w1(0)=0.5, f(0)=2, c2=5000,

  b=0.2, λ(0)=40, C0=1000 ma=95

The parameter values of ‘a’ and ‘b’ can be estimated for any given dataset outside the normative model by considering equation (1). Though these parameters are mutually correlated with w1(t) and w2(t), due to the interdependence between the two, one effort can be expressed in the form of the other. In this investigation, the main aim is to check the importance of allocation of the testing effort (w1), we use genetic algorithm to allocate testing effort.

Below figure shows the optimal allocation of testing effort with respect to time.

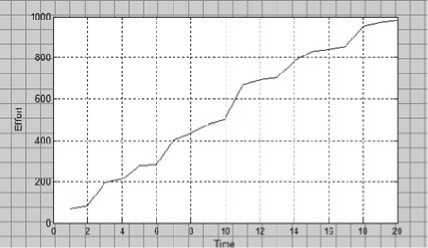
Fig 1: Allocation of testing effort w 1 versus time

• VI.    Software Release Policy

In this segment we will discuss the optimal time to handover a software product from development stage to operational stage. The literary meaning of the term ‘to release’ is to specify that the software has met a defined quality level during testing and is ready for mass distribution.

An ideal software release policy addresses the following concerns of a release manager:

• •    Avoid excessive time to market due to over testing.

• •    Manage all product associated activities, from idea to retirement

• •    Optimize product performance and plan upcoming investments

• •    Manage and increase the software products reliability.

• •    Balance client wants for reasonable price, delivery on time and a reliable product.

• •    Determine whether the software product is good enough to release to client, minimizing the risks of releasing software with serious problem.

For a given total fault content in software ‘a’ we generate initial population to solve this problem. And we used all above parameters.

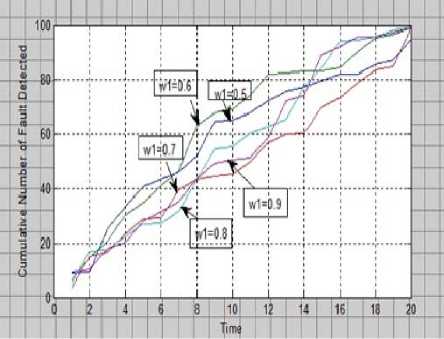
Fig 2: Cumulative number of faults removed versus time.

Table 2. Parameters of the GA for cumulative fault removing

Parameter	Value
Population Size	20
Number of Generations	80
Selection Mode	Tournament
Crossover Probability	0.8
Mutation Probability	0.2

In this study, the main goal is to check the significance of distribution of testing effort (w 1 ). Hence, its value has been supposed to be constant during the life cycle. During this analysis the value of w 1 is gradually increased keeping the other parameters constant and the rate of fault removal increases quickly.

The proper implementation of release decision depends on whether or not the software will be transferred from its development stage to operational stage. In other words, it is a trade-off between primary release to capture the profit of prior market introduction, and the delay of product release to enhance functionality or to improve quality. Testing and debugging process play a vital role in software release policy. For given total cost of the software, we generate initial population to solve these problems. Figure show the optimal time to release software.

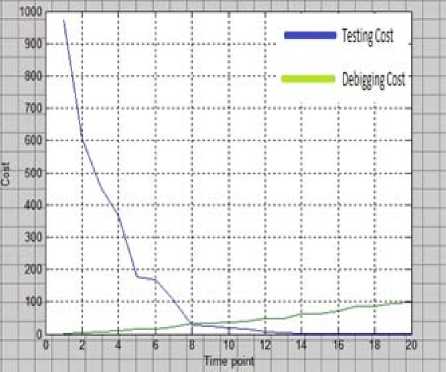
Fig 3: w1=0.9

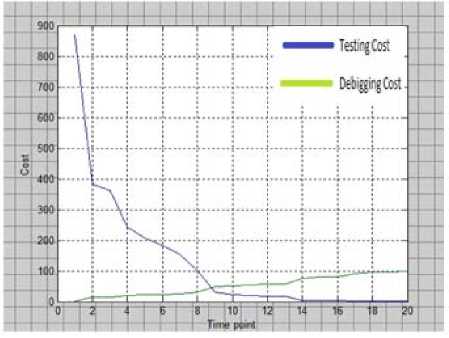
Fig 4: w1=0.93

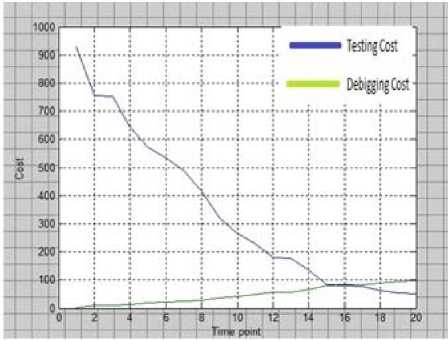
Fig 5: w1=0.95

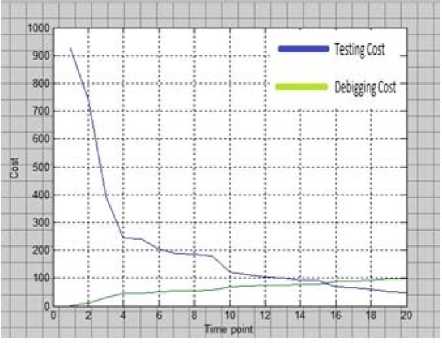
Fig 6: w 1 =0.97

From the above investigation, it can be concluded that as the value of w1 decreases, the point of interaction between the cost of fixing and cost of detecting gets delayed. And, at the same time, it takes longer period to intersect them. From the above mathematical exercise it is very clear that the better time to release software is when the interaction point of fixing and detecting cost lies under minimum cost criterion.

• VII. Conclusion

In this paper, we propose an alternative foundation for optimal allocation of testing resources using genetic algorithm. Using the control theoretic approach, we recommend that software testing and debugging should be viewed as simultaneous behaviors. During the investigation, we have examined allocating effort in dynamic environment using genetic algorithm. Also, we have examined that due to the experience curve phenomenon, the effort required to fix an error keeps on decreasing with time. At the same time, testing effort keeps on increasing as in the later stages of a planning period it becomes tough to detect faults. So company employs more efforts to detect the remaining faults. Using the proposed methods, we can easily control the consumption rate of testing effort expenses and discover more and more faults in a definite time interval. This means that the developers and testers can devote their time and resources to complete their testing tasks based on well controlled expenditures. This paper also studies the optimal resource allocation problems for various conditions by examining the behavior of the model parameters. A detailed optimization policy based on genetic algorithm is proposed and numerical examples are also exemplified. The release problem is also discussed. The software product’s success depends on the time of its introduce time in the marketplace. In such instance, we need to conclude the optimal stopping time for testing. Based on theoretical and empirical study in this paper, we observed that the optimal release time of software is the time point where the total cost incurred due to correction coincides with the cost of detection maintaining the strict reliability constraint. Otherwise, the organization will wait for perfect time.