Dynamic Model on the Transmission of Malicious Codes in Network

This is the world of internet services and internet users are increasing exponentially. Computer systems now contain millions of records relating to commerce, healthcare, banking, defense and personal information. All this information is at risk of either being misused for fraudulent purposes or modified for malicious reasons. Malicious software, or malware, on the Internet can cause serious problems, not only for services like email and the web, but for electricity, transport and healthcare services due to their increasing Internet dependence. One of the serious threats to the Internet and Computer network is malware attack.

Malicious code is any code added, changed, or removed from a software system in order to intentionally harm the system. Though the problem of malicious code has a long history, a number of recent, widely publicized attacks and certain economic trends suggest that malicious code is rapidly becoming a critical problem for industry, government, and individuals. Traditional examples of malicious code include viruses, worms and Trojan Horses. In these days networking is widespread, malicious code mostly use the sneaker net to spread over the network.

One of the various ways in which computer systems canbe compromised is by deploying computer virus/worms.

There have been instances in the past where virus/worms have virtually brought the Internet to a grinding. Currently, e-mail is one of the main sources for transmission of virus, worms and Trojans.

A computer virus attaches itself to a program or file enabling it to spread from one computer to another, leaving infections as it travels. A computer virus can damage hardware, software or files of the systems. Computer viruses have been around from the days of DOS and even earlier, but after the 1990s, they became a potent threat due to the popularity of the internet and removable media. Some reported Viruses are I Love You, Logic Bomb and Melissa.

I Love You (2000) - "I Love You" virus is a computer virus that successfully attacked tens of millions of computers in 2000 when it was sent as an attachment to a user with the text "ILOVEYOU" in the subject line.

A computer worm is a code that infects computer system and is able to spread functional copies of it without depending on other codes. Worms spread from computer to computer, but unlike a virus, it has the capability to transmit without any human intervention. Due to the copying nature of a worm and its capability to travel across network the end result in most cases is that the worm consumes too much system memory, causing web servers, network servers and individual computers to stop responding. Some reported worms are Code Red, Slammer.

Code Red (2001) - Code Red was a computer worm observed on the Internet on July 13, 2001. It attacked computers running Microsoft's IIS web server. Although the worm had been released on July 13, the largest group of infected computers was seen on July 19, 2001. On this day, the number of infected hosts reached 359,000.

Slammer (2003) - Slammer worm caused a denial of service on some Internet hosts and dramatically slowed down general Internet traffic. This fast-moving worm managed to temporarily bring much of the Internet to its knees in January 2003. It spread rapidly, infecting most of its 75,000 victims within ten minutes.

A Trojan horse is a program that secretly performs its operation under the guise of a legitimate program. The Trojan horse at first glance will appear to be useful software but will actually damage once installed or run on the computer. When a Trojan is activated on the computer the results can vary. Some Trojans are designed to bebe more annoying than virus and worms as they can cause serious damage by deleting files and destroying information on system. Trojans are also known to create a backdoor on computer that gives malicious users access to system, possibly allowing confidential or personal information to be compromised. Unlike viruses and worms, Trojans do not reproduce by infecting other files nor do they self-replicate. Some reported Trojan horses are remote access Trojans (RATs), backdoor Trojans (backdoors) Distributed Denial of Service Attack Trojan horse

Distributed Denial of Service Attack Trojan horse - A lot of computers can be tricked into installing the Distributed Denial of Service Trojan so that the hacker can gain control over one, several or all computers through a client that is connected with a master server. Using the primary computer within one huge zombie network of machines, hackers are able to sent attacks at particular targets, including companies and websites. They simply flood the target server with traffic, thus making it impossible for simple users to access certain websites or systems. Often these attacks are used to stop the activity of famous brands that could handle different financial demands.

The distribution of Malware attack is depicted in Fig.1

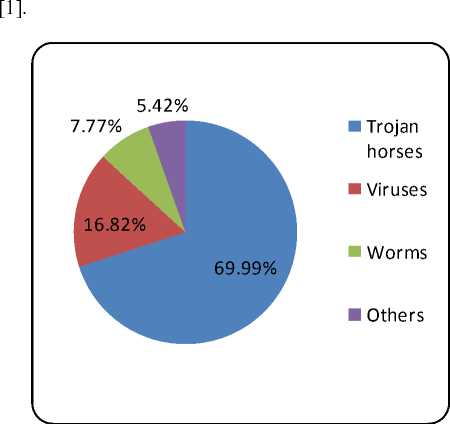
Figure 1 : The distribution of malicious attack in March 2011

Transmissions of virus, worms and Trojans in computer network are similar to biological infectious diseases and are epidemic in nature. One of the most basic procedures in the modeling of diseases is to use a compartmental model, in which the population is divided into different groups. The dynamics of the model are governed by the system of differential equations. The similarity between the spread of a biological virus and computer virus propagation encourages researchers to apply an epidemic model to the network environment.

Today, people rely on computers to create, store and manage critical information. Information transmitted over networks has a higher degree of security risk. Thus, it is crucial to protect the computers and data from loss, damage and misuse. Antivirus programs are an effective way to protect a computer against virus, worms and Trojans. An antivirus program protects a computer against malicious codes (virus, worms and Trojans) by identifying and removing them when found in memory, storage media or in any incoming files. One technique that antivirus programs use to identify a virus is to look for virus signatures or virus definitions, which are known specific patterns of virus codes. Most commercial antivirus products make use of a black listing strategy. They rely on databases of virus signatures that are consulted when a new program arrives. Anti-virus tools scan disks and sometimes e-mail looking for known viruses. Updating the antivirus program’s signature files regularly is important as it will download any new virus definitions that have been added since the last update. In this paper we have critically analyzed the effect of antivirus in our model that is; an analysis has been made to study the dynamic behavior of the system with and without antivirus installed in the nodes.

The subsequent content of this paper is organized as follows: Section 2 describes related works. Section 3 introduces S _i IR model, its variable and parameters. Section 4 describes equilibrium points, basic reproduction number and global stability of the infectious-free equilibrium point. Section 5, finally summarizes the work with simulated results.

• II.    RELATED WORKS

The strong desire to understand the spread mechanism of malicious codes has motivated the proposal of a variety of epidemic models that are based on fully connected networks, that is, networks where each computer is equally likely to be accessed by any other computer. Transmissions of virus, worms and Trojans in computer network are similar to biological infectious diseases and are epidemic in nature. The similarity between the spread of a biological virus and computer virus propagation encourages researchers to apply an epidemic model to the network environment. One of the most basic procedures in the modeling of diseases is to use a compartmental model, in which the population is divided into different groups. The dynamics of the model are governed by the system of differential equations.

Previous work in this direction was focused mainly on the theoretical study of complex dynamical properties of the models, such as the global stability of equilibriums, the emergence of periodic solutions, and the occurrence of chaotic phenomena.

Mathematical epidemiology seems to have grown exponentially starting in the middle of the 20th century (the first edition in 1957 of Bailey’s book [2] is an important landmark). Kermack and McKendrick developed the classical epidemic models and obtained the epidemic threshold to show that the density of susceptible class must exceed a critical value in order to take place an epidemic outbreak [3], [4], [5]. As the attack of malicious codes in computer network is epidemic in nature, researchers used the classical epidemic model of Kermack and McKendrick to develop e-epidemic models on the transmission of malicious objects in computer network and their immune system [6], [7], [8], [9]. In recent years, more attention has been paid on the research of virus and worm propagation model and antivirus countermeasures to study the dominance of virus and worms, depending on the network parameters [10], [11], [12]. McCluskey studied on the SIR model with delay and proved the global asymptotically stability of the SIR model [13]. Mishra-et-al performed an analysis on SEIRS (Susceptible-Exposed-Infected-Recovered) and SEIQRS (Susceptible-Exposed-Infected-Quarantine-Recovered-Susceptible) dynamical system by considering variable parameters, fuzzy epidemics, differential epidemics and analyzed the stability of the disease free equilibrium points to have a better understanding to avoid infections in a computer network [14], [15], [16], [17]. Piqueira-et-al used the epidemiological models to describe the analogy between disease propagation and virus propagation [18], [19].

• III.    MODEL FORMULATION

According to the modeling methodology, an important part of the model formulation process is to clearly identify the assumptions made in the model while abstracting from the real world situation to the mathematical model.

The basic assumptions of our model are as follows:

• •    The entire population can be divided into five states namely susceptible class-1, susceptible class-2, susceptible class-3, Infectious class and Recovered class based on their epidemiological status.

• •    Every new node added to the network is initially susceptible and few of them are infected.

• •    The active population includes all the nodes.

• •    The rate at which new nodes are added to the network and the existing ones which die due to noninfection reason are assumed to be constants.

• •    All the model parameters are positive constants.

• •    The per capita contact rate is independent of the total population size.

• •    All interactions are homogeneously occurring.

Another important demand of the modeling methodology is to identify and describe the different variables and parameters used in the model formulation process.

The model starts with some basic notation:

• •    S 1 (t) represents the number of susceptible nodes due

to virus at time t.

• •    S 2 (t) represents the number of susceptible nodes due

to worms at time t.

• •    S 3 (t) represents the number of susceptible nodes due

to Trojans at time t.

• •    I(t) represents the number of infectious nodes at time t.

• •    R(t) represents the number of recovered nodes at time t.

• •    N(t) represents the total number of nodes at time t.

The parameters used in the model are as follows:

• •    b is the constant rate at which new nodes are added to the network.

• •    d denotes the death rate of nodes due to natural or non- infectious reason.

• •    β denotes the infectivity contact rate .

• •    µ is the recovery rate.

• •    δ is the death rate due to attack of malicious codes

( virus, worms and Trojans ).

• •    θ is the rate of vertical transmission.

• •    p_i is the probability of recruiting nodes from b number of nodes for i^th susceptible class and E i=3 p i = 1 so that the input flow into i^th susceptible class is bp_i ( i = 1, 2, 3).

An e-epidemic S_iIR (susceptible class-1, susceptible class-2, susceptible class-3, infectious class and recovered class) model illustrates the dynamics of direct transmission of virus, worms and Trojans in the computer network. The newborn susceptible can be distributed into three susceptible groups namely, S 1 ,S 2 and S 3 based on their inherent susceptibility. We assume that, there is a vital dynamics and the population has homogeneous spatial distribution and the mixing of nodes follow the law of mass action. The local density of the total population is assumed to be constant throughout the total population. The total population size is N, that is, N = S _i + I + R (i = 1, 2, 3 ) may vary with time.

The flow of virus, worms and Trojans in computer network is depicted in Fig 2.

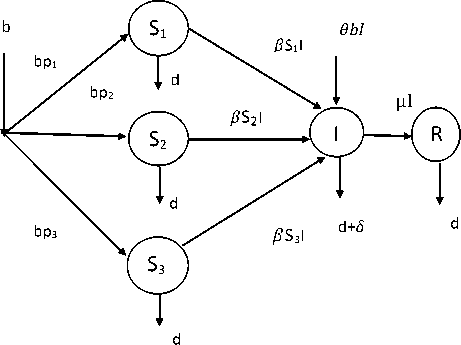
Figure 2: The flow of virus, worms and Trojans in computer network

Our main interest is to investigate transmission dynamics of virus, worms and Trojan horse. Based on our assumptions in the computer network, the transmission dynamics consists of the following system of ordinary differential equations:

di dt

dS_i                                a

= =3 »" PS i l — ^dS ,

= pi ^^ S [ — (d + ц + 6 — 9b )I *

dR

— = |Л — dR            ,

... dN

Thus, = dt

b — dN — (8 — 9b )I

equilibrium by E⁰ = (S 1 , S 2 , S 3 , I = 0 ) . Analyzing the local stability of E⁰ gives the epidemic threshold conditions under which the number of infected individuals will either increase or decrease to zero when a small number of infectious nodes are introduced into a fully susceptible population. These threshold conditions are characterized by the reproduction number, denoted by R 0 .

Eliminating R, system (1) reduces to

In the absence of the attack of virus, worms and Trojan the population size of the node N approaches to b/d. The differential equation for N implies that the solution of (1) starting in the R⁺ 5 either approaches, enters or remains in the subset

G = {(S 1 ,S 2 ,S 3 ,I,R)/ S 1 ≥ 0, S 2 ≥0, S 3 ≥ 0, I ≥ 0, R ≥0, S₁ +S 2 +S₃ +I+R /d}.

This implies that the solution in the region G and the equations defined by (1) exists and are unique on maximal interval. Since the solution remains bounded in the positive invariant region G, the maximal interval is [0, ∞ ). Thus initial value problem is well posed both mathematically and epidemiologically.

di dt

dS dt^ = bpt— eSil — dSi i = 3

ei2

S i — (d + ц + 5 — 9b )I

i = 1

J

We derive a formula for the reproduction number R ₀ by investigating the local stability of E⁰.

The Jacobian of (2) at E ⁰ has the form

J =

I

—d

—d0

0           —(d + p + 5 — 0b") + pb/ d

• IV. EQUILIBRIUM POINTS AND BASIC REPRODUCTION NUMBER

Equilibrium points are the points where the variables do not change with time. In order to know about the evolution of infected nodes, that is, the number of infected nodes increases indefinitely or not, we study the stability of equilibrium points.

• A. Equilibrium points

For equilibrium points we have,

^ = 0 (i = 1, 2, 3); - = 0; — = 0

dt                        dt         dt

All the Eigen values of J have negative real part if and only if — ⁽d + p + 5 — 0b) + — < 0

'                   '                             d о                 n         Pb

So we assume, Rn = —,--------7

⁰     d (d+p +5 — 0b )

Theorem 1: The attack-free equilibrium is globally asymptotically stable if R0 < 1.

Proof. From first equation of (2), we have

dSi

— < bp i ^{— dS} i

dSi dt <

d^)

Or, St(t) < -p-L — (— — Si(0))e dt V t > 0 in the set d ' d ‘

G.

Now from second equation of (2) we have,

We get,

di (t ) dt

Infectious free equilibrium E ⁰ = ^ -p¹ , -^ 2 , -p³ , 0^ and

Endemic equilibrium

i =3

= pi^Si — (d i =1

+ 5 + p — 0b) i

/(d+p +5— 0b )p i ⁽ d +p +5 — 0b)p 2 (d+p +5— 0b ) p 3

V p ' p ' p pb—(d+p+5—0b )dA

P (d+p +5 — 0b ) / .

B. Basic Reproduction number and global stability

An important part of modeling transmission of virus, worms and Trojans is the Basic Reproduction number, denoted by R0. The Basic Reproduction number also helps us predict who will not become infected at all.

System (1) has an infectious-free equilibrium in which the component of infective is zero and other susceptible components are positive. This denotes infectious-free

i =3

i(t) = i (0)Exp {pi'^Si — (d + 5 + p—0b)} i =1

Or, i⁽t⁾ = i (0)Exp(R₀ — 1)Exp⁽d + 5 + p— 0b) Hence, i ⁽t) ^ 0 as t ^ да for R₀< 1 in the set G. To prove the global asymptotic stability of E ⁰ in G we only need to show that ( - 1 - , ^p2^—- , ^p■ 3 ^—- , 0) is globally asymptotically stable in П = { S_i >  0, i = 0, i = 1,2,3^}.

The first equation of (2) in П reduces to

■df^L i —dS_i ; i =1,2,3.

Or, bp_i — dS_i = ke^—dt ; where k is constant.

Or, S_t (t) = ^ - {— - S t (0)}e^-dt d d

S_i (t) ^— as t^ ^ , V i =1,2,3.

d

Theorem 2: The system (2) has a unique endemic equilibrium, if and only if, R₀ > 1 and the endemic equilibrium is locally asymptotically stable.

Proof. From the first equation of (2).

bpi - eSil - dS 0(3)

i =3

pI^^- (d + ц + 5 - 9b )I = 0

i = 1

I = 0 or Z=3     - (d+^+8-9b ) = 0(4)

i = 1 pi+d           pb

Hence there exists an endemic equilibrium, if and only if, there exists a positive solution I to (4)

Let, F(l) = Z =1

i =3

f'(i) = -Z i =1

p i     (d + ^+8-9b )

Pi+d          pb

^PP i (ei+d)²<

1) were chosen to suit a real malware attack scenario. Runge-Kutta Fehlberg method of order 4 and 5 were employed to solve and simulate the system of equations (1).

The behavior of the system with and without the run of antivirus software can be observed from Fig. 3 and Fig. 4 respectively. Comparisons can lead to a better understanding, so from Fig. 5 we observe the behavior of the infectious class of the system with and without antivirus software. In the system without anti-virus the number of infected nodes are high and the infection persist for a long period but the system having updated anti-virus software recovers faster and has less number of infected nodes. Fig. 6 shows that the recovery of the system is very high when we use anti-virus software. From Fig. 7 we observe the behavior of the Infectious class versus Recovered class in the system with anti-v irus software. The crashing of nodes due to the attack are very less and the recovery of the nodes are high in the system (approx 88%) having antivirus software which can be clearly observed from Fig. 7.

This shows the strength of our model. The simulation results, supported by the theoretical approach showed that all malicious codes were able to pervade if the reproduction number is less than one.

Hence F(I) is decreasing function

lim F (I) =

I^ w

d + p + 5 - 3b eb

< 0

When, d + p + 5 >  0b

Then there exists a unique positive solution of

F(I) = 0 ; iff F (0) > 0

i = 3

F ® = D

2—i d i = 1

d + p + 5 - 0b

eb

Or, F(0) =    (R0 - D dRg

There exists a unique endemic equilibrium points if and only if R0 > 1.

The Jacobian of (2) at E * has the form

J=

I

-d

-d

-PbP 1 /d

-Pbp 2 /d

-Pbp g /d

— (d + p + 5 — 0b) + pb/ d_

All the Eigen values

of J have negative real part.

Hence, E * is locally asymptotically stable.

V. CONCLUSION

Inspired by the biological compartmental models, an e-S i IR ( i=1, 2, 3) e-epidemic model for the transmission and control of virus, worms and Trojans in computer network is developed. The initial parameter values (Table

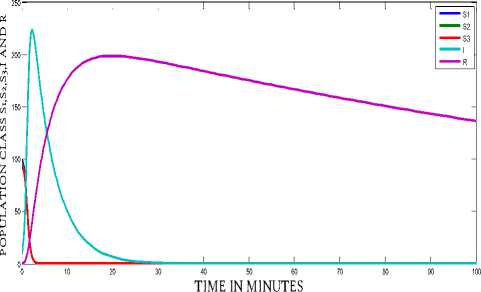
Figure 3 : Dynamical behavior of the system with anti-virus software (f = 0.15)

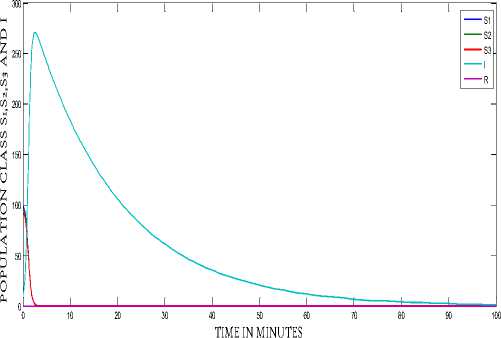
Figure 4: Dynamical behavior of the system without anti-virus software (p = 0)

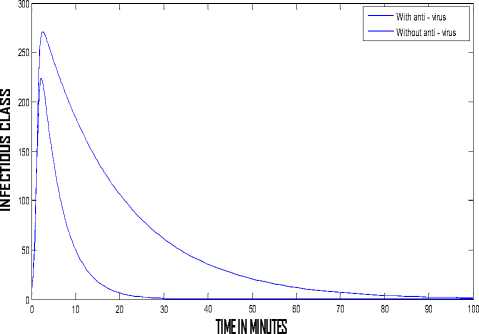
Figure 5 : Behavior of the infectious class versus time with and without antivirus software (ц = 0.15, ц = 0 )

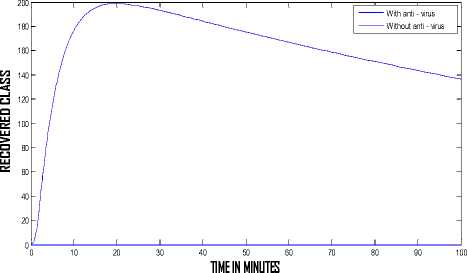
Figure 6: Behavior of the recovered class versus time with and without antivirus software (ц = 0.15, ц = 0)

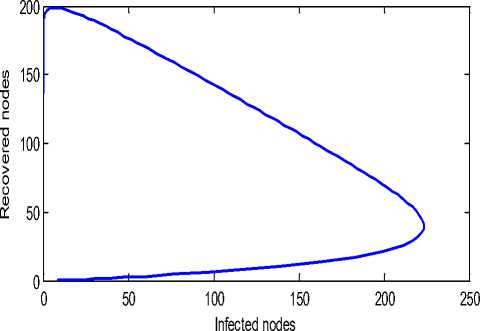
Figure 7: Recovered class versus Infectious class with anti-virus software

TABLE I.        Parametric values used to simulate the

SYSTEM

Parameter name	Initial Value
Number of susceptible node due to virus at time t ( S 1 (t) )	S 1 (0)=100
Number of susceptible node due to worms at time t ( S 2 (t) )	S 2 (0)= 97
Number of susceptible node due to Trojans at time t ( S 3 (t) )	S 3 (0)= 94
Number of Infective nodes at time t ( I(t) )	I(0)= 9
Number of recovered nodes at time t ( R(t) )	R(0) = 0

Infectivity contact rate ( β )	0.01
Death rate due to attack ( δ )	0.05
Birth rate ( b )	0.01
Recovery rate in infectious class ( µ )	0.15
Natural death rate ( d )	0.01
Rate of vertical transmission ( θ )	0.003
Recruitment rate of susceptible class for virus ( bp 1 )	0.004
Recruitment rate of susceptible class for worms ( bp 2 )	0.003
Recruitment rate of susceptible class for Trojan ( bp 3 )	0.003