Dynamic stability of a straight pipe conveying pulsatile flow under thermal loads

PNRPU MECHANICS BULLETIN

Fluid conveying pipes find applications in a number of areas of engineering. They are widely used in the petroleum industry for transportation of oil and gas. Another broad use of them is in the transport of water. Pipelines are also primary structural parts in power plants, hydraulic systems, air-conditioners, refrigerators etc.

Nanoscale tubes find application in nanophysics, nanobiology and nanomechanics as nanofluidic devices in nanocontainers for gas storage and nanopipes conveying fluid. The experiments at the nanoscale are difficult and expensive. That is why the continuum elastic models have been used to study the fluid-structure interaction. The carbon nanotubes are considered with Euler- and Timoshenko-beam models [1–9].

The flow of the fluid in the tube causes oscillations in it. The dynamic characteristics of the pipe’s oscillations depend on the velocity and the mass of the conveyed fluid. For pipes conveying fluid with a constant velocity it is known that the natural frequency of the pipe becomes lower when the velocity of the transported fluid increases. The velocity of the fluid corresponding to a natural frequency equal to zero is called critical velocity. At that point the system is at the edge of loss of stability. When the pipe conveys pulsatile flow, the pipe loses stability even though the mean velocity of the fluid is smaller than the critical velocity [10].

The research of the dynamic stability of pipes conveying fluid is branched into two directions: a) dynamic stability of pipes with a rectilinear axis [11–25] and b) dynamic stability of curved pipes [27–32].

The oscillations of a pipe with a flowing fluid, supported at both ends, were investigated in [36]. The global properties of the spectrum in dependence on fluid velocity, tube and fluid material densities, magnitude and direction of longitudinal force are established.

In [37] the linear stability of elastic collapsible pipes with flowing fluid is investigated, in the case when the equilibrium configuration of the pipe is helical. The geometric-variational approach was applied to study the 3D dynamics of collapsible pipes.

The dynamic stability of elastic membrane axisymmetric tubes filled with fluid was investigated in [38]. The considered fluid is non-viscous and incompressible.

Thermal loads may induce excessive vibration in the system, leading to loss of stability. Therefore, analysis of the dynamic stability due to thermal loading is essential for the safe operation of the pipeline.

The most common methods used for dynamic analysis of the pipes conveying fluid are the Transfer matrix method (TMM) and the Generalized differential quadrature method (GDQM). The both methods have significant advantage from the Finite element method (FEM). The conventional FEM can be very time consuming when it comes to investigation of a pipeline with a high number of spans. The order of the overall property matrices for the whole multispan pipeline increases with the number of spans. This is unlike the TMM in which the order of the overall transfer matrix is independent on number of spans and is kept unchanged.

The GDQM approximates a derivative of a function in the partial differential equation of the lateral vibration of the pipe at any discrete point as a weighted sum of the function values at all discrete value at the domain. The main advantage of the method is its high convergence with a small number of grid points.

The paper is structured as follows. First, it is presented the model of the pipe and the governing differential equation of its transverse vibration. The Galerkin method is employed to approach the solution of the problem. The Floquet theorem is applied to investigate the stability of the trivial solution. Finally, the obtained results from the numerical solution are presented and several important conclusions are summarized.

1. Problem formulation

The present paper uses the Euler-Bernoulli beam theory to investigate the dynamic stability of a pipe of length l , conveying fluid and and subjected to thermal load T . The pipe, shown in Fig. 1, is hinged at its both ends.

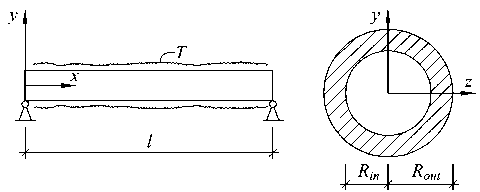
Fig. 1. Static scheme and cross-section of the investigated pipe

The transverse vibration of a straight pipe conveying pulsatile inviscid fluid and under thermal load is governed by the following differential equation

4    22

EI— + mV2 + EAa T)+ 2mV---+ d x4 v f            ’X x2 f d x d t dV d w         d2 w A

+ m,+ m, + m„   = o 0, f dt dx v f    p) dt2

where t is the time, w ( x , t ) is the lateral displacement of the pipe axis, x is the coordinate along the axis, EI is the rigidity of the pipe. The mass of the pipe per unit length is denoted by m _p and the mass of the fluid per unit length of the pipe by m _f . V is the flow velocity of the fluid in the pipe. A is the area of the cross-section of the pipe. α is the coefficient of linear thermal expansion of the material of the pipe.

The fluid velocity is the following harmonic function of the time t

V = V ₀ ( 1 + 5 cos ( to f t ) ) ,

where V 0 is the constant fluid rate, 5 is the excitation coefficient and co f is the fluid pulsation frequency.

The spectral Galerkin method is applied to approximate the solution of the boundary value problem (1). According to this method, an approximate solution is sought in the form [33]:

nl

EJ { ( m f ⁺ m ) ^{yz + 2} mV ( 1 ^{+ 5 cos} ( ^o t ) ) yz ⁺ i = 1 0

+ [ EI ?⁴ y +

m f V ( 1 + 5 cos ( o ft ) ) + EA a T

— m f V ₀ 5 co f sin ( o f t ) y I J z i } y_k dx = 0.

y_i II

—

n w (x, t )=E yi(x) zi( t).                 (3)

i = 1

In this expression z i ( t ) are unknown functions. y i ( x ) are basic functions satisfying the boundary conditions of the tube. The eigenfunctions for the pipe with stationary fluid ( V = 0 ) are used as basic functions in the present paper.

For a Bernoulli-Euler tubular beam filled with stationary fluid, one has

5 4 w /          \ 5 2 w

EI    +(mf+ mp)    = 0.

d xd

Free vibration of the beam has the form w (x, t ) = y (x) e o 1,(5)

where ю is the natural frequency of the beam and i = V— 1.

The substitution of (5) in (4) yields

У" ( ^x ) = Y 4 y i ( ^x ) ,

where

( m f + m p ) ^o 2

EI

Substituting (3) in equation (1) one obtains the residual function, which does not vanish identically since w ( x , t ) is not exact solution of equation (1). Here, and in the sequel, dots denote derivatives with respect to t and primes denote derivatives with respect to x .

For the solution of system (10) is employed the described in [33] method. The beam is divided to sections with length of A x . The integrals in (10) are expressed in the following form

Jyypdx = { y} T {у. }A x(11)

l

J yIykdx = { yI}T {Ук }A x(12)

l 1

J y"ykdx = —{Mi}T {yk }Ax(13)

In equations (11), (12) and (13):

{ y i } is a column vector of the lateral displacements of the nodes on the axis of the pipe, corresponding to the i -th eigenform of a pipe with stationary fluid;

{ y I } is a column vector of the rotations of the nodes on the axis of the pipe, corresponding to the i -th eigenform of a pipe with stationary fluid;

{ M i } is the vector of the bending moments associated with the i -th mode shape { y i } .

The substitution of (11), (12) and (13) in (10) yields

n

£ { ( m f ⁺ m p )^{ y i ^{} T {} y k ^{} z} i ⁺ i = 1

^{+ 2} m f V ( 1 ^{+ 5} cos ( m fl ) ) { y i } ^T { y k } z +

R (x,t) = E {(mf + mP) УЛ + i=1

+ 2 m_fV₀ ( 1 + 5 cos ( o ft ) ) y I z i + EIy"z i +

+[ Ell * { y } T { y' . } +

1 г

+--

EI [

m_fy₀ 0 ( 1 + 5 cos ( o _ft ) ) 2 + EA a T { M i } ^T { y_k }

—

+

m f V ( 1 + 5 cos ( o f t ) ) + EA a T

y_i ^II z_i

—

— m_fV₀ 5o _f

sin ( o f t ) y ' z, } .

^{— m} f У o ^5o} sin ( ^o t ){ y ' } T { у . } J z } ^{A x} = ^{0    (14)}

Writing equation (14) in matrix form gives:

According to the standard Galerkin procedure, the residual function R ( x , t ) should be orthogonal to the basic functions in the area x e [ 0; l ] :

|M| z + | C ( t )| z + | K ( t )| q = 0             (15)

The equation (15) could be transformed in the following form

l

J R ( x , t ) y k ( x ) dx = 0, for k = 1,..., n          (9)

The result of the application of (9) is a system of n differential equations about the unknown functions z i ( t ) . This system for the differential equation (1) is:

where

I 0

0 M

^{ q ^{} +}

0     — I

K ( t ) ^C ( t )

{ q } = 0,

{ q } ^T = { q 1 = ^z i ;...; q n = z n ; q n + 1 = ^z i ;...; q 2 n = ^z n }   ⁽¹⁷⁾

After some transformations for equation (16) one obtains

{ q } = A ( t ){ q } = 0 (18) where the coefficient matrix | A ( t )| is periodic with period T , that is | A ( t + T )| = A ( t )| .

The Floquet theorem is applied to investigate the stability of the trivial solution { q } = 0 . According to the theorem the solution of the system (18) has the following form

{ q ( t ) } =Ф ( t ) { q ( 0 ) } (19) where |ф( t )| is the fundamental matrix, solution of the T – periodic system (18). The funda-mental matrix has the following form [34]

| Ф( t )A L (t) eB (20)

In (20) L (t) is a periodic matrix that has an initial val ue L (0) = I. B is a constant matrix.

The matrix |ф( T )|

is known as monodromy matrix.

p = 7800 kg / m 3 . The density of the flowing fluid is p = 1000 kg / m ³.

The finite element method was used to obtain the basic functions y, ( x ) . The eigenfunctions for the pipe with stationary fluid ( V = 0 ) are used as basic functions in the present paper. The first 14 modes were used in the present calculations.

The stability of the system is determined by the modules of the eigenvalues of the monodromy matrix (characteristic multipliers).

If all of the characteristic multipliers have modulus less than one, then the zero solution is asymptotically stable.

If all of the characteristic multipliers have modulus less than one or equal to one, and if the algebraic multiplicity equals the geometric multiplicity of each characteristic multiplier with modulus one, then the zero solution is Lyapunov stable.

If one or more of the characteristic multipliers has modulus greater than one, then the zero solution is unstable.

For the pipe in Fig.1 is obtained the critical value of the constant fluid rate V _{0, cr} for different values of the thermal load T , excitation coefficient 5 and the fluid pulsation frequency co _f . The results are shown in Fig. 2 and Fig. 3.

The eigenvalues of |ф( T )| are known as characteristic multipliers. The stability of the system is determined by the modules of the characteristic multipliers of the periodic system (18) [34].

In principal the fundamental matrix is difficult to be determined in an analytic way, but there are methods to approximate it [35]. The period T is divided into k subintervals A t . For each time interval is calculated the matrix

I A ⁽ t ) .

A = A

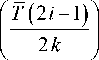
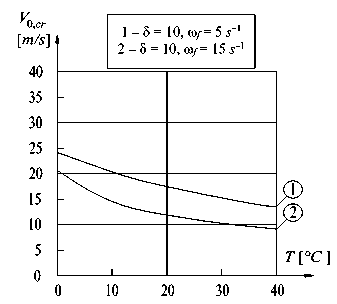
Fig. 2. Critical value of the constant fluid rate versus the thermal load for 5 = 10

Then the monodromy matrix |ф( T )| is calculated on the following formula

Ф( T ) = 1ПеАА '

i = 1

2. Numerical results

Numerical studies have been carried out for the system in Fig. 1.

The geometric and the material characteristics of the pipe are: the inner and the outer radii of the cross-section of the pipe are R in = 0.012 m and R out = 0.014 m , Young’s modulus E = 210 GPa , coefficient of linear thermal expansion a = 10 - 5 C ^{- 1}, the density of the material of the pipe

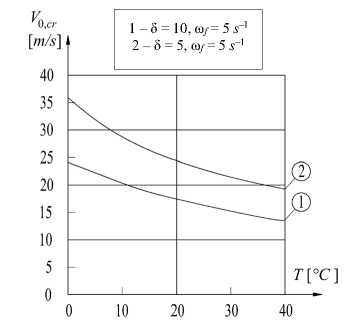
Fig. 3. Critical value of the constant fluid rate versus the thermal load for co , = 5 s ^{- 1}

The obtained results show that the temperature load has a destabilizing effect on the pipe – with increasing the temperature the critical velocity decreases.

Conclusion

Thermal loads on a structure could affect its integrity if they are not taken into account in the design process. The structures are subject to daily and seasonal temperature changes due to their exposure to outdoor air temperature, solar radiation or underground temperature. In the past thermal stresses have caused failures in the structures. Understanding the effect of the thermal loads on the structures, and how to minimize them, significantly reduces the risks of failure or serious damages and prevents from high repair costs.

In the present paper is studied the influence of the temperature on the stability of a pipe conveying pulsatile flow.

The employed Floquet theory, in the case when the fluid velocity is a harmonic function of the time t , allows the