Dynamical theory of X-ray diffraction in crystals based on two-dimensional recurrent relations

To describe diffraction in lateral crystals of a rectangular cross section, two-dimensional recurrent relations were obtained [1, 2], which differ from the one-dimensional Darwin algebraic equations. On the other hand, diffraction in perfect crystals of a rectangular cross section can also be considered using the two-dimensional Takagi-Taupin equations [3]. On the example ofa cylindrical crystal, it was shown that twodimensional recurrence relations can be used to calculate reciprocal space maps (RSMs) for crystals of arbitrary shape [4]. It should be noted that numerical integration based on the Takagi-Taupin equations is not always stable, while calculations based on two-dimensional recurrence relations are always stable. In this paper, we show that the diffraction of spatially restricted X-ray beams in periodic structures can be described using two-dimensional recurrence relations. Using these recurrence relations, it is possible to calculate the x-ray fields inside the crystal and RSMs.

Recurrent relations

Two-dimensional recurrent relations can be written in the following form

m n	m- 1 = a T n- 1	+ b 1	m- 1 S n- 1
m S n	m- 1 = aS n +1	+ b 2	m- 1 T n +1

where Tnm and Snm are the amplitudes of the transmitted and diffracted wave, a = (1 — iqn) exp (i . 2nd„ ),

,                   0            λ sin θB ,

/   2nd \                  /2

• —i q exp i .       , b2 = —i q exp i .,

\ A sin OB /                    \ A sin OB /

• q0 = — A sin eB X0,     9 = — a sin eB X-g.

• - _{λ s} ^π _in ^d _{θ B}χ g , χ ₀ , χ h and χ -h — are the Fourier components of the X-ray polarizability, d = 2~:— g '^s *^^e interplanar distance, λ is the X-ray wave length, θ B is the Bragg angle for

reflective lattice planes. The distance between nodes along the x axis is есть A x = d/ tg O B .

Figure 1a shows the directions of the transmitted and diffracted X-ray beam, taking into account the dynamical interaction of X-ray waves. The horizontal lines represent the crystal planes, which are numbered from top to bottom. Arrows directed down correspond to transmitted waves, arrows directed up refer to diffracted waves.

According to Figure 1a, the magnitude of the amplitude T m of the transmitted beam at the node ( m ; n ) consists of the contributions of the transmitted T _n ^m _- ^- ₁ ¹ and reflected downward S m^{- 1} waves at the node ( m — 1; n — 1) . This physical process is described by the first equation of recurrent relations (1). The diffraction wave S m at the node ( m ; n ) is formed as a result of the upward passage of the wave S _n ^m ₊ ^- ₁ ¹ and the

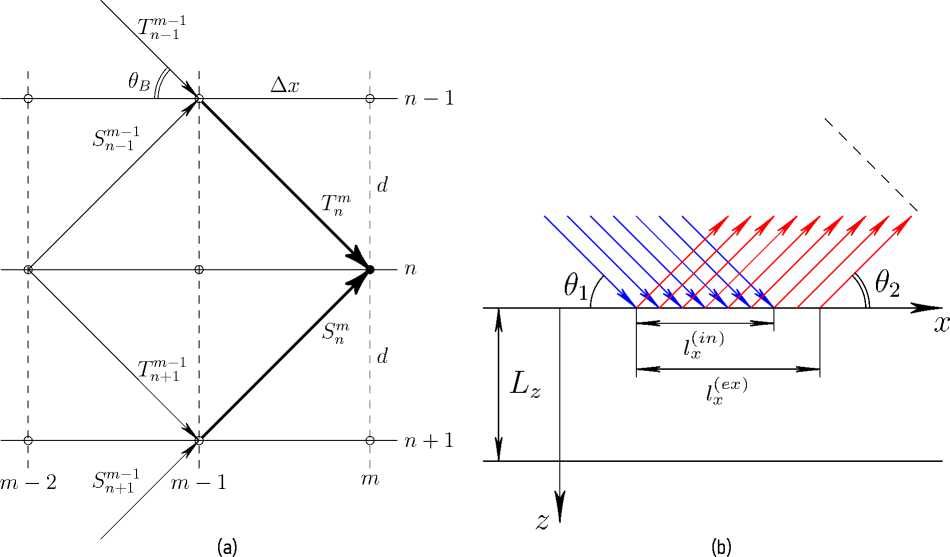
Figure 1. (a) Scheme of two-dimensional X-ray diffraction on discrete crystal lattice planes. The vertical coordinate (see (b)) is defined as z = nd , where n is the number of the crystal plane. The horizontal coordinate is x = m Д x , where Д x is the lateral distance between the nodes, m is the node number. (b) Geometry of X-ray diffraction. The incident restricted beam illuminates the surface of the crystal l Xn ) . The exited beam size is l Xex ) .

Рисунок 1. (a) Схема двумерной дифракции рентгеновских лучей на кристаллических плоскостях. Вертикальная координата определена как z = nd , где n — номер кристаллической плоскости. Горизонтальная координата: x = m Д x , где Д x — расстояние между узлами в латеральном направлении, m — номер узла. (b) Геометрия дифракции рентгеновских лучей. Ширина падающего на кристалл пучка l Xn ) . Ширина выходящего пучка l (ex ) .

diffraction of the wave T m-1 ¹ at the node ( m — 1; n + 1) .

The exponential factor exp

i

2 nd \ λ sin θ _B

which is included

in the coefficients of the recurrence relations, takes into ac-

count the phase variation during the passage of X-ray waves from one crystal plane to the neighboring plane.

To solve the diffraction problem, recurrent relations (1) must be supplemented with boundary conditions (Figure 1b). Let the X-ray beam fall on the crystal surface at an angle 6 1 , which, in the general case, may differ from the Bragg angle θ _B . We consider the case when an incident X-ray wave illuminates the crystal surface l xin ) , then the boundary condition has the form

istered, for example, at a different angle 6 ₂ . In this case, it is necessary to take into account additional phase variations ф _т = — (2 n/X ) m Д ж cos 6 ₂ for the reflected X-ray wave at the front of the exited beam, which is shown by the dotted line in Figure 1b.

The intensity of the diffracted X-ray wave is found from the relation:

I _h ( q _x , q _z ) =

M x              2

^ S m exp(iф m )

m

¹ о =

i ^π cos λ

6 1 ■ m Д ж)

m Д ж ^ l xin ) ,

T m = 0 ,  m Д ж>1 Хin ) .

2π sin θB where qx =  x (Д61 - Д62), qx = — 2n cos 6B (Д61 + д62), д61 = 61 — 6b, Д62 = 62 — 6b .

It follows from relations (2) that the modulus of the amplitude of the incident X-ray beam on the crystal surface is equal to unity. The exponential factor takes into account the change in the phase of the incident wave amplitude along the x axis (Figure 1b).

The calculation of the amplitudes of X-ray fields is performed on the basis of recurrence relations (1) taking into account the boundary conditions (2) for all nodes of a rectangular network ( m ; n ) , where 0 <  m <  M x = l Xin ) / Д ж and 0 ⩽ n ⩽ N _z = L _z /d , L _z is the thickness of the crystal.

In a triple-axis diffraction scheme, the exited beam is reg-

Calculated results

Numerical calculations of X-ray diffraction in a perfect silicon crystal are performed for symmetric (333) reflection of σ –polarized X-ray CuK _{α 1} radiation. The calculation results are presented taking into account the shift of the coordinate system by the angular distance associated with the X-ray refraction, which is proportional to the real part of the coefficient a ₀ in the diffraction equations (1). The length of the primary Bragg extinction for (333) reflection from silicon is l ext = λ| sin θ B |/ ( Cπ|χ h | ) = 8.03 µ m. The Bragg angle for the selected reflection is 47.476 arc. deg. The interplanar distance of the reflecting planes is d = 0 . 1045 nm.

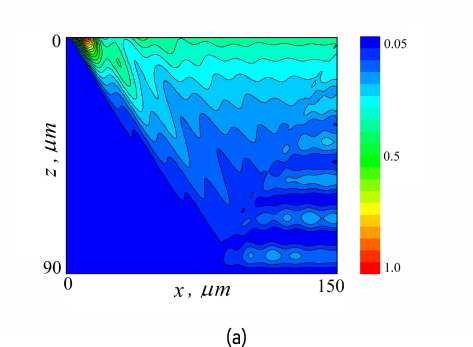
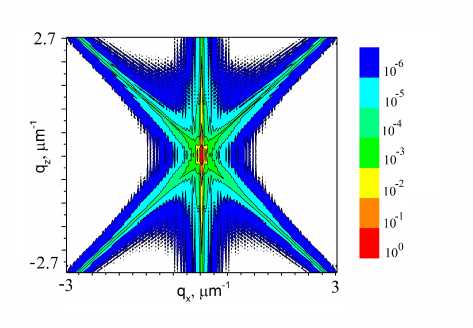
Figure 2. (a) The calculated distribution of the diffraction intensity inside the crystal at a deviation from the Bragg angle by 2 arc. sec. (b) RSM on a logarithmic scale, calculated on the basis of two-dimensional recurrence relations. The width of the incident and diffraction beams is 110 µ m.

Рисунок 2. (a) Распределение интенсивности дифрагированной волны внутри кристалла при отклонении от угла Брегга на 2 угловые сек. (b) Карта интенсивности в логарифмическом масштабе, рассчитанная методом рекуррентных соотношений. Ширина падающего и отраженного пучков 110 µ m.

(b)

Using recurrent relations (1), the field of the diffracted wave inside the crystal was calculated for an arbitrary angle of incidence, which differs slightly from the Bragg angle. Figure 2a shows the scattering intensity distribution inside the crystal when the incident beam deviates from the Bragg angle by 2 arc.sec.

Solution (3) makes it possible to calculate RSMs for various sizes of X-ray beams. Figure 2b shows the calculated RSM on a logarithmic scale, which completely coincides with calculations based on differential diffraction equations. The width of the incident beam is 110 µ m. The effective depth of penetration of X-ray wave into a crystal is 82 µ m.

The study was supported by the Russian Science Foundation, grant No. 23-22-00062.