Earth Observation Satellites Scheduling Based on Decomposition Optimization Algorithm

Published Online November 2010 in MECS

Earth Observation Satellite is a kind of satellite which uses its optical or other remote sensing imaging equipment to observe ground targets and generates corresponding images. The satellite’s routing job is controlled by uplink instructions which are transformed from schedules generated by the ground systems. Imaging satellites scheduling means to assign satellite resource and execution time to imaging tasks under the satellite operational constraints in order to maximize the number of tasks that could be completed [1].

The satellite imaging process can be shown as figure 1.

Corresponding author: Feng Yao.

Copyright © 2010 MECS

Restricted by its orbit, a satellite will pass a ground target for limited times, and imaging operation must be executed within time windows that the satellite can catch sight of the target. For a target which is deviated from the ground trace of the satellite, the satellite or the sensor onboard must roll itself to aim at it. If the roll angles for different targets are not the same, the satellite must switch its attitude between different imaging activities, thus requiring enough transition time left. For example, there is not enough transition time between imaging of target B and target C, so only imaging target B after target A or imaging target C after target A is possible.

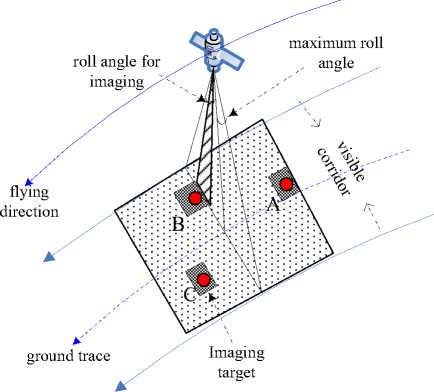
Figure 1. Satellite Imaging Process

Therefore, scheduling of a imaging satellite can be regarded as a single machine scheduling problem with time window constraint and setup time correlative with task order[2]. The problem was proved to be NP-hard[3], and was solved mainly by heuristic algorithm[4,5], neighborhood search algorithm[6-8], and meta-heuristics such as genetic algorithm[9].

As the number of imaging satellite continually increased, multi-satellites imaging scheduling became a research hotspot[1,5,7]. Multi-satellites imaging scheduling is more difficult than single satellite scheduling for the following reasons. First, the number of alternative satellites and alternative time windows for a imaging task is multiplied, making the combinational characteristic of the problem more prominent. Second, operational constraints of different satellites may be different, making uniform modeling of the problem difficult. To cope with these difficulties, most research made some simplifications to abstract those common main constraints and constructed mix integer programming model[5] or constraint satisfaction problem models[1,7]. Then approximate algorithms were used to solve the models. Such methods were effective in some cases, but when problem scale was large, computation time would be too long or computation result would be relatively poor.

In research on the problem of cooperative earth observing by multiple satellites, Morris[1] proposed an idea which first assigned observation tasks to different satellites, then solved single satellite scheduling problem for each satellite. The essence of his method was to transform multi-satellites scheduling problem into single satellite scheduling problem to decrease problem complexity and improve computational efficiency. Its task assignment process lied in a higher level and would greatly affect the scheduling effect, since task assignment process divided the tasks into several non-intersecting subsets and dissevered the relations among them. But how to find a good task assignment strategy to ensure the method’s performance is itself a quite difficult problem. Morris didn’t give a clear answer for it.

This paper used Morris’ decomposition idea as a reference and decomposed the imaging satellites scheduling problem into a task assignment main problem and a single satellite scheduling sub-problem. The difference was that, Morris’ method assigned tasks to satellites only once according to some strategy, while our method deemed task assignment as an optimization process also, and used an adaptive ant colony optimization algorithm (ACO) to generate different task assignment solutions. Based on these solutions and the following single satellite scheduling processes, we could get different complete schedules. Then assessment results of these schedules were fed back to ant colony optimization algorithm to guide it to find better task assignment solutions and complete schedules. Tests on different scale problems showed that our algorithm was effective.

• II.    Modeling of Imaging Satellites Scheduling Problem

Imaging satellites scheduling problem can be described as a quintuple <  E , 5 , T , C , F >  . E is scheduling horizon. 5 = { S i , - , Sn_s } is a set of satellites.

T = { t , l , T N } is a set of tasks. C is a set of constraints.

F is objective function . Imaging satellite scheduling can be classified into long-term scheduling and shortterm scheduling. Short-term scheduling as this paper considered requires precise orbit prediction data, so its horizon is usually shorter than 24 hours.

Due to a imaging satellite’s field of view, it can see only a strip on the earth at one pass, so big area must be segmented to narrow strips along with the satellite’s ground trace. For multi-satellites case, different satellite’s ground traces may be not parallel, so segmenting target areas into small spots that can be observed completely by either satellite in one pass is a feasible way. For simplification, we assumed that all the observing targets were spot targets in this paper.

Each observing task must satisfy time interval, sensor type, ground sample distance or other requirements. For a given task, there may be more than one satellite that can fulfill it. Each candidate satellite may have several time windows with the task in a given time period. Each time window means a specific roll angle for the corresponding satellite. These time windows and roll angles can be obtained ahead of schedule through orbit calculation and prediction software.

For a task T_i , we define all of its time windows as a set

N S N ij

° . = UU O k ,^{1 G[1, L ,} N T ^{] ,} j = 1 k = 1

where N_T is the number of tasks, N_S is the number of satellites, N _j is the number of time windows between satellite S_j and task T , O _jk is the k th time window. g _jk is the roll angle of S_j observing T in O _jk . [ ws _jk , we _jk ] is the corresponding time interval of O _jk . p is the priority of T . d is the imaging duration for T .

For a satellite S_j , its rolling velocity is r_j , the stabilizing time needed after rolling is h_j , the memory needed for unit duration time of imaging is a j , the maximum storage capacity is M_j , the maximum times of imaging operations in the given scheduling horizon is R_j . x _jk is the decision variable which is defined as

• Г 1, task T is scheduled to satellite S j in time window O jk k [ 0, else

.

For imaging satellites scheduling problem, the following constraints must be satisfied.

• (1)    Exclusivity, namely each task should be scheduled only once and without interrupt, i.e.

N S N j

£^ X jk <  1, V . G [1, L , N t ]              (1)

j = 1 k = 1

• (2)    There must be enough time left for a satellite to switch its roll angle between two successive imaging operations. This time includes transition time and the stabilizing time after a switch, i.e.

we k ⁺ I g ijk - g i'jk' ^|/ r j ⁺ h j <  wsi'jk '

V / € [1, L , N s ], x j_k X_v jk . = Ш we ijk <  WS^.

• (3)    The amount of image data stored onboard should not overstep the capacity of memory instrument, i.e.

N T N ij

EE x ijk d a j < M j , ^V i ^€ W^ N s ^]         (3)

i = 1 k = 1

• (4)    The times of imaging operations are limited due to the satellite’s power and maneuverability constraints, i.e.

N_T N ij

EE x -k <  R j , V j € [1, l , N s ]             (4)

• i = 1 k = 1

To sum up, the imaging satellites scheduling problem discussed in this paper is to assign satellite resources and imaging time to tasks subjected to the above constraints, with an optimization objective of maximizing the sum of all the scheduled tasks’ priorities. Thereby, we establish a 0-1 integer programming model of the problem as follows.

N T N S N ij max EEE X jk p = 1 j = 1 k = 1

N S N j

EE <  1

^j = i k = 1

we ak ⁺ d i ⁺ I g -jk - g j I / r j + h j <  ws -'jk ' ,

• ^{V x}^k^xi■^k■ = 1 ^ we ijk <  wsi'jk'

N^N ib                                 (5)

st J EE ^X _l jk da_J < M j

.. N ; v

EE ■ < R i=1 k=1

• i ,    Г € [1, L , N t ]

j € [1, L , N s ]

^ k , k € [1, l , N j ]

• III.    Framework of Solving Method

Considering the computational complexity of the above model, we propose a solving method based on problem decomposition. The original problem is decomposed into a task assignment main problem and a single satellite scheduling sub-problem. Its framework can be shown as figure 2.

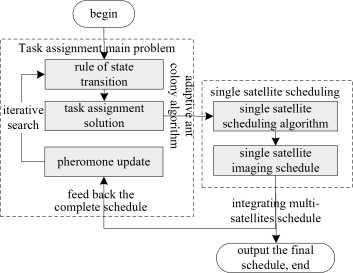
Figure 2. Framework of Decomposition-Based Solving Method

In figure 2, the task assignment main problem considers a set of tasks T = { t , l , T N } and a set of satellites S = { S 1 , L , S N } . Task T_t has a set of alternative satellites S ( i )( S ( i ) c S ) which not only can satisfy its imaging requirements such as ground sample distance, sensor type, etc., but also have time windows with it. The problem requires assigning a satellite to each task, and each task should be assigned to not more than one satellite.

Given a set of tasks T ^' which are assigned to satellite S_j , the single satellite scheduling sub-problem requires optimally selecting and scheduling tasks under the satellite operational constraints in order to maximize the number of tasks that could be completed.

The framework adopts adaptive ant colony optimization algorithm to solve task assignment main problem. In the iterative searching process, as soon as a task assignment solution is generated by the ants, it is sent to each corresponding satellite to carry on single satellite scheduling. The schedules from each satellite are integrated to obtain a complete schedule and assess performance of the task assignment solution. These assessment results are then used to guide ant colony optimization algorithm to find better task assignment solutions. After a number of iterations, a final optimized task assignment solution and corresponding multisatellites imaging schedule is acquired. In such a framework, the single satellite scheduling module can be regarded as the attractiveness calculation function in ant colony optimization algorithm.

• IV.    Adaptive ACO Algorithm for Task Assignment Main Problem

Ant colony optimization algorithm is originated from the swarm behavior of ants searching for food [10]. It has already been successfully applied in a serial of difficult combinatorial optimization problems. Since its positive feedback characteristic and random searching ability are outstanding, we construct an adaptive ant colony optimization algorithm for the task assignment main problem.

A.    Definition of Pheromone and Its Initialization

In TSP applications, pheromone often denotes the probability of getting better route if node j is arranged right after node i . Similarly in our algorithm, we define pheromone as the probability of assigning a certain task to a certain satellite, which is in accordance with the information that assigning that task to that satellite tends to get a better schedule. Let S ( i ) be the number of alternative satellites for task T_i . The probability of assigning T i to satellite S_y is defined as r.. . As initialization, the probability of assigning a task to each candidate satellite is set to be identical, i.e.

^T ij (°) = ^7 , i =1, l , N t , ^j =1’ L ’I S ( i ) (6)

S ( i )

B.    Construction of Solutions

When ants construct solutions, an ideal manner is to get feasible solutions at any time, meaning that tasks are assigned under all the constraints. But computation time needed in this manner is too long since imaging satellite’s operational constraints are very complex. Besides, searching randomicity of ant colony optimization algorithm will be affected if feasible solution is required each time, thus the algorithm’s performance will be degenerated[11]. In order to avoid this defect, we assume to consider only the constraint (1) as shown in section II when ants constructing solutions, other constraints are left for single satellite scheduling module to cope with. So in solution construction phase, we only need to select a certain satellite for a given task from its alternative satellites according to stated rule of state transition.

We adopt a pseudo-random proportion rule[10] to select satellite for a task. Let a, = n- denote that task Ti choose satellite j0 to fulfill it. The rule for making a choice is as follows:

max

= <  J =[ 1,1 $ ( - ) ]

{ j t ) } ^,if q <  q о

C

. Ф ,

otherwise

q is a random number distributed uniformly in [0,1], q0 is a control parameter for random selection, 0 < q0 < 1.

When q < q0, satellite is selected according to amount of pheromone. When q > q0 , ф means to select satellite according to the following probability distribution:

Pr( - , J 0 , t ) =

^T -J 0 ⁽ t )

E ^{т (} t )

j =[ 1,1 $ ( - я ]

, - =

[1, N t J j e [1,| $ ( - )]

Pr( i , ₀, t ) denotes the probability of select satellite

₀ for T_i at time t .

C.    Pheromone Update

• 1)    Local Update Rule

Every time a solution Sol is constructed by the ants, it will be sent to single satellite scheduling module, then be further repaired (will be explained in section E) to get a new solution Sol ' . If Sol ' is better than Sol , pheromone would be accordingly updated locally. The update manner is as follows:

^{T (} t + 1) = ^{(1 -} P local T ⁽ t ) + P . ^{T (0)} , ^{V c} / = $ot       ⁽9)

P _local = ( 0,1 ) is a local pheromone evaporation parameter. The local pheromone update rule can be seen as a diversification mechanism which can avoid getting into local optimum too early.

• 2)    Global Update Rule

The purpose of global pheromone update is to reinforce pheromone of better solutions in order to guide the search more intelligent. Elitist strategy uses the best solution of each iteration to update pheromone, which tends to lead to early convergence[10]. Rank-based strategy ranks solutions of each iteration first, then updates pheromone according to weighted order information[12]. We adopt a best solution queue (BSQ)

strategy to make global pheromone update. In BSQ, several current best solutions are always kept. If better solutions are got in iterating process, they will be replaced into BSQ. Each time an iteration is completed, BSQ will be updated, and pheromone will also be updated in term of the following mode:

^T -j ⁽ t + 1) = ⁽¹ — P global Уу ⁽ t ) + P global ^{At (10)}

P global = ( 0,1 ) is a global pheromone parameter, while Ат _-к is the increase pheromone calculated as follows:

evaporation amount of

A r j =<

^X E ^T -r ⁽ t ),^{if ст} /= BSQ

0,

otherwise

X is a pheromone increment factor.

D.    Adaptive Strategy

Ant colony optimization algorithm bears a contradiction of quickly convergence and stagnant precocity. The strategies used to improve global search ability and avoid early getting in local optimum include, combining determinate selection with random selection, or change some parameters to dynamically adjust pheromone [13,14]. We adopt an adaptive parameter adjustment strategy to dynamically suite searching process.

Let parameter q ₀ has a domain of { q 0 , q 0 } , q 0 ' <  q b , parameter P global ^has a ^{domain of} { P global , P^ b'l } , P‘_slobal <  P btobat . If the current best solution hasn’t been improved after 3 1 times of successive iteration, we may suspect that the algorithm got in a local optimum, following search may not jump out or jump out too slowly. At this time, q ₀ may be assigned a small value q ₀ ^a , meaning high randomicity of satellite selection, in order to improve the possibility of jumping out local optimum and realizing a global search. At the same time, decreasing P _global may reduce corresponding pheromone of the current best solution, which will also help to get away from local optimum. After a local optimum is jumped out, the two parameters will be assigned big values q 0 and P g _lobal to improve converging speed.

Besides, since pheromone update is continuously, differences between pheromone may be remarkable, causing the search process easily got into stagnation. Only increasing the probability of random selection or change the rate of pheromone evaporation would not lead the search process out of local optimum. So, we adopt the idea of pheromone smoothing. When the current best solution was not improved for successive 3 2 times, each satellite’s pheromone would be weighted averaged with the highest value among them. Such a method will minish the differences between pheromone when the algorithm get into stagnation, thus be propitious to lead it getting out of local optimum.

E.    Solution Repair

The above algorithm presents a task assignment result each time it generates a solution. After the single satellite scheduling is finished, some tasks may not be arranged due to satellite capability limitation. We may try to adjust them to other satellites, meaning try to insert them into another satellite’s schedule list. If an insertion is feasible, then the task assignment scheme is accordingly modified. This solution repair process can realize fine-tuning for the task assignment result and improve the solution quality. The detailed process is not complex and is omitted here.

• V. The Single Satellite Scheduling Sub-problem

Single satellite scheduling can be looked upon as a single machine scheduling problem with time-window constraint and task order dependent set up time. Restricted by its orbit, a satellite has only limited imaging chances or visible time windows with a given target. Thus, single satellite scheduling with short horizon can be simplified to a task selection problem[8]. For smallscale single satellite scheduling problem, even complete searching algorithm can be used to get an optimal solution.

By our method, each time the ACO algorithm adopted here generates a solution, single satellite scheduling will be performed, so single satellite scheduling algorithm must be quick enough. We adopted a Heuristic Algorithm (HA) and a Very Fast Simulated Annealing algorithm (VFSA). Accordingly, we call our decomposition optimization method using HA algorithm as ACO-HA, while the method using VFSA as ACO-VFSA.

A.    Heuristic Algorithm

HA selects optimal choices in turn according to some heuristic rules in its searching process, so it has very fast computation speed and the result is easy to explain. HA is an approximate algorithm in common use in satellite scheduling. Scheduling of ASTER, SPOT-5 and Landsat 7 satellite all use this kind of algorithm. Literature [4] provided some rules for task selection by synthetically considering task priority, sensor parameters and imaging quality. We consider conflicts between tasks except for task priorities, and define the concept of conflict degree for a task. If one task was scheduled, then conflict degree of that task would be the sum of the priorities of those not scheduled tasks impacted by the scheduled task. Let conflict degree of task T_i be Conflict_i , its calculation formula is:

Conflict_i = ∑ p_j (12)

T _j ∈ ConflictSet_i

ConflictSet_i is the set of tasks that could not be scheduled because of T_i ’s impact. Conflict degree reflects the degree of confliction between one task and the others. Based on this concept, our algorithm follows such a simple idea: schedule those tasks of small conflict with others firstly, with the expectation that more tasks will be scheduled. As figure 3 shows, there are conflicts between Task2 and Task1 or Task3, if we first schedule

Task2, then Task1 and Task3 could not be scheduled both, so we should schedule Task1 or Task3 firstly.

Figure 3. conflicts between tasks

Here, conflict between tasks mainly indicates time conflict, meaning that if there is not enough transition time between two tasks, then we take it for a conflict. The process of our HA algorithm is described as follows:

Step1: order the tasks according to task priorities, schedule the task with highest priority first.

Step2: for tasks with same priorities, calculate their conflict degrees, schedule the task with small conflict degree first.

Step3: for tasks with same priority and same conflict degree, schedule the task with small roll angle or early start time first.

B.    Very Fast Simulated Annealing Algorithm

Heuristic algorithm requires in-depth comprehension of the problem itself. Since the algorithm selects task according to given rules and doesn’t allow backtrack, its performance relies heavily on good heuristic rules and has no guarantee. To get better single satellite imaging schedule, we also try to use a simulated annealing algorithm. General simulated annealing algorithm has better global search ability, but need adequate perturbation and iteration numbers, with deliberate annealing plan, therefore its efficiency is still under improvement. As said before, in each iteration of our ACO algorithm, single satellite scheduling must be carried through for each satellite according to task assignment result. To avoid unacceptable time cost, single satellite scheduling must be quick enough. Ingber and some others improved perturbation and annealing manner for general SA and proposed a Very Fast Simulated Annealing algorithm [16, 17], which greatly increased the computation speed. We adopt the VFSA algorithm to solve our single satellite scheduling problem.

• 1)    Solution encoding

Considering the neighborhood design, we arrange the tasks on each satellite according to the start time of their time windows, thus an activity list with time precedence is constructed. This method is convenient for setup time calculation and other constraint check to ensure new solution feasibility.

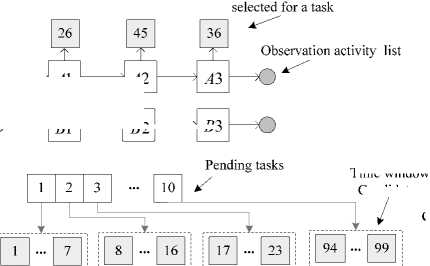
Besides, since satellite scheduling is usually an oversubscribed problem that only part tasks could be scheduled, we design a virtual satellite resource, which is used to virtually undertake all the tasks that could not be assigned to real satellites. The difference between virtual and real satellites is that all tasks assigned to virtual satellite are not restricted by time window or other constraints and their values are zero. Figure 4 is a denotation of solution encoding for a problem including 2 satellites and 10 tasks.

Number of time window satellite:

A 2

B 3

B 2

Figure 4. denotation of solution encoding

A 1

B 1

Virtual

• 2)    Model perturbation

VFSA adopts a pseudo-Cauchy distribution depending on temperature to perturb the current model and generate new solutions. We construct some neighborhood structures according to the problem feature. Moving between neighbors will perturb the original model and generate new solutions. Perturbations to a solution include task changes and task time changes.

For task change, we adopt the X - interchange method or named Swap/shift move method. In detail, we use the 1-0 node interchange and 1-1 node interchange method. 1-0 node interchange will insert a task assigned to one certain satellite to another satellite when feasible. 1-1 node interchange will swap the places of two tasks originally assigned to two different satellites when feasible. For single satellite scheduling, since there is only one real satellite and one virtual satellite, this method essentially means to swap tasks between real satellite and virtual satellite.

For task time change, we adopt an exchange neighborhood, namely randomly switch a task from one of its time window to another.

• 3)    Acceptance probability

VFSA adopts such an acceptance probability formula according to generalized Boltzmann - Gibbs distribution:

P = [ 1 - (1 - q ) ^ E / T ] q ⁾             (13)

Here, A E is energy difference, namely the difference between new solution and original one. q is a real number, different value of q means different preference of adventuring. Low value of q means that the acceptance probability will take a risk to make some bad solutions accepted more likely, while the computation speed will be improved, thus the value of q must be properly selected. When q ^ 1 , the acceptance probability will be just the same as it of general SA:

P = exp( -A E / T )                   (14)

• 4)    Annealing plan

Since annealing speed is an important factor to decide efficiency of the algorithm, we adopt a fast annealing strategy:

1/ N

T_t = V                   (15)

Here, k is the number of iteration, a is the rate of temperature attenuation, N is a given parameter. The smaller N is, the faster temperature descends. Usually, it can be assigned a value of 1 or 2.

• 5)    Terminate rules

To cut computation time, we adopt a dual-level terminate rule. The outer level is based on temperature, while the inner level is based on non-update of solution, namely when the current best solution is not improved for certain iterations, the search process will terminate. Our algorithm will terminate as long as either one of the conditions be satisfied.

VI. Experiments

Since there are still not acknowledged benchmark test problems in satellite scheduling research area, we use a random generation method to test our algorithm. The test problems are generated according to the following rules:

• (1)    Generate targets within an area between north latitude 20°~50° and east longitude 70°~130° according to a uniform distribution. Requirements of sensor type and ground sample distance are ignored. The number of targets M is respectively 100, 200, 300, 400 and 500.

• (2)    The number of satellites N is respectively 3, 4 and 5.

• (3)    The priorities of tasks are randomly selected among [1,10].

• (4)    The time windows between a task and a satellite are acquired by the Satellite Tool Kit software [18].

• (5)    Duration of a task imaging activity is 5~9 seconds.

• (6)    Different scale problem instances are generated through different combination of M and N.

Parameters of VFSA was set to q = -1 , a =0.95 , N =1. Parameters of ACO were set as table I shows.

TABLE I.	parameters set for ACO
parameters		meaning
AntSize = 8 MaxIter = 300 P loca = 0.1 P global = 0.6, P global = q 0 a = 0.55, q 0 b = 0.85 5 1 = 50 5 2 = 90	0.8	number of ants max iteration number local pheromone evaporation coefficient min and max value of global pheromone evaporation coefficient min and max value of parameter denoting randomicity of satellite selection the iteration number threshold for calling adaptive parameter adjustment strategy the iteration number threshold for calling pheromone smooth strategy