Economic Designing of PV/FC/Wind Hybrid System Considering Components Availability

The fast process of industrialization and growing population during the past years caused the increase of electricity consumption. Limitation of space and the slow improvement of the networks also caused some areas with high load density which could result in declining of power quality and voltage collapse. At the same time, non-urban areas are witnessing poor performance of the networks like high voltage drops and high losses along the distribution lines [1]. In contrast, despite limitations in networks and available financial resources, utilities are also hardly trying to expand and boost networks. In this way, distribution generation could be one of the suitable options. One of the solutions for increasing economic efficiency in renewable power plant is using different hybrid systems. The sun and wind are two main sources in renewable energies which seem to devote a large portion of generating energy in future.

The supplied energy from these resources is predictable and as a result the power of these power plants and their storage systems will be considered much more than the amount of load power demand, to increase load reliability and availability. In hybrid systems, the generation predictability with combining the several resources is increased and in fact these resources cover each other’s deficits. From this perspective wind and the sun have presented suitable overlap for each other, so the power of units and also necessary storages in combining wind-sun units compared to only wind unites or sun units have been significantly reduced.

Various definitions are presented for reliability, but the definition that is widely accepted is as follows; Reliability is the probability of a system or a component correct operation under exploitation condition in specified time [2].

Reliability calculations are major issues which should be considered along with economic and environmental evaluations resulting from using energy renewable sources. Accurate evaluation of economic profit used from these units needs investigation of rate of systems` reliability. Obviously, available energy limitation in renewable energy sources and also its discontinuous behavior reduces level of system reliability [3-5].

Various methods are presented for minimization of hybrid power plant costs. Wide range of optimization methods, from classical combination like linear, nonlinear analytical and numerical programming mainly based on partial derivatives calculation to applying modern intelligent algorithms like Genetic algorithm and particle swarm optimization (PSO) are used in different researches.

In [6] a hybrid system consists of wind turbine and fuel cell is studied for improving profitability of wind power. In another study, wind farm equipped with Superconductor Magnetic Energy Storage (SMES) is studied [7]. SMES is suitable for improving power quality. In [8] hybrid system consists of solar array, fuel cell and SMES is investigated. Unit sizing determination and PV/Wind/FC hybrid system costs analysis is analyzed in [9]. In another study, performance and sizing of PV/Wind/FC hybrid system is considered [10]. In study [11], the method of determining optimal sizing of PV/Wind hybrid system is depicted independent from stand-alone clearly. In a similar study, capacity of diesel generator with wind turbine is optimized [12].

In this paper the effect of considering reliability indices is investigated along with economic factors for design an optimal combination for PFWHS with minimum cost and maximum of responding to load power demand. To obtain an optimal design using an intelligent algorithm seems more effective according to extent of variables and magnitude of objective function. In this paper PSO algorithm is used for optimization. Also to investigating the impact of component availability rate on system under study costs and reliability due to failure and repair rate of system components and uncertainty in wind speed and solar irradiance, two scenarios are considered. In first scenario the availability of all components is considered 1 and in second scenario isn’t considered 1 because of

In this paper the PFWHS modeling is presented in section II. The optimal sizing problem and the objective function are described in section III. In section IV, PSO algorithm is presented and in section V, the optimization results are analyzed and finally in section VI is concluded the results.

• II.    MODEL OF PFWHS

A schematic diagram of PV/FC/Wind hybrid system (PFWHS) consists of PV array, wind turbine (WT), electrolyzer (EL), hydrogen storage tank (HST), fuel cell (FC) and inverter is shown in Fig. 1. The PV array and wind turbine work together to satisfy the load demand.When the total generated energy of the PFWHS is greater than the load demand, the extra energy will be supplied to feed the EL for hydrogen production. Also when the total generated energy of the PFWHS is lower than the load demand, the deficit energy is compensated by FC until the hydrogen of HST is depleted.

failure and repair rate of components and uncertainty in wind speed and solar irradiance.

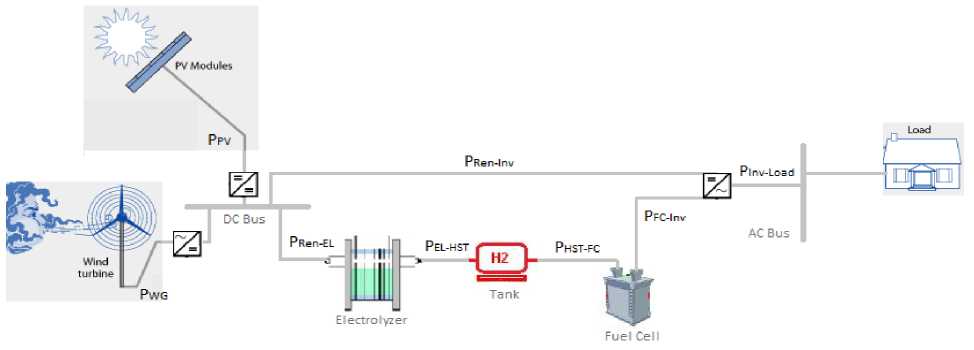
Figure 1.The schematic diagram of PV/FC/Wind hybrid system

• A.    PV Mode

Photovoltaic (PV) [13] converts solar radiation energy to electrical energy. PV temperature and solar radiation changes bring about changes in PV voltage level and output power as follow

• B.    Wind Model

The simplified model to simulate the power output of a wind turbine [14] can be defined by

P pv = 0.001 G X P pv , rated X ^ pv , conv                         (1)

G ( t, 9 pv ) = G v ( t ) cos ( # pv ) + G h ( t ) sin (⁶ pv )           ⁽²⁾

Where, G is perpendicular radiation at array’s surface (W/m2), PPV,rated is rated power of each PV array at G= 1000W/m2, and ηPV,conv is the efficiency of PV’s DC/DC converter and Maximum Power Point Tracking System (MPPT). ƟPV is the PV panel tilt angle, GH(t) and Gv(t) are the horizontal and vertical components of solar irradiation. It should be noted that, temperature effects are neglected here.

p ( v ) = W ⁽ )

PR

v W = v W X

—

vC

—

h

v

vC

v

(

A

V ^h'ef J

v <  v„and

C

V

v >  vF

J

Pv

Where, Rrefers to the rated power, C is the cut-in vv wind speed, R is the rated wind speed and F is the cut- h off wind speed. vW is wind speed at a specific height, vref vW wind speed at the reference height (href)

• C.    EL Model

Water by EL can be decomposed into its elementary components. This process is done by passing electrical current between two electrodes that are separated by an aqueous electrolyte [15].

The energy delivered to HST from EL can be calculated as follows:

P EL - HST = ^P Re n - EL ^X Л EL                         (5)

Where pen-EL is delivered power to EL and nEL is efficiency of EL.

• D.    HST Model

Physical HS is one of the storage techniques that use HST to store compressed hydrogen. After compressing under high pressure, the hydrogen which is required by PEMFC is sent from the HST [16].

The stored energy in HST for each step-time can be calculated by

E    ( t ) = E    ( t - 1) + P         ( t ) A t - P          ( t ) A t n

HST ⁽) HST ⁽   ) EL - HST ⁽)     HST - FC ⁽) HST

Where Phst-fcis delivered power to FC from HST and n hstis HST efficiency.

The stored energy in HST can’t exceed the following constraints as follows:

^EHST , Min ^{- E}HST ⁽ t ) - ^EHST , Max                  ⁽⁷⁾

^EHST ⁽ t = ^{0) — E}HST (8 ⁷⁶⁰ )                    ⁽⁸⁾

• E.    FC Model

FC converts oxygen and hydrogen chemical energy to electrical energy during which some heat and water is generated as well [17]. FC output power can be defined by

P FC - Inv = P HST - FC ^ FC                        ⁽⁹⁾

Where nFC refers to efficiency of FC.

• F.    Inverter Model

The inverter is electrical device to convert electrical power from DC into AC form at the desired frequency of the load. The power delivered to load from inverter is calculated by

P inv - Load   ⁽ P FC - Inv ⁺ P Re n - Inv ). ⁿ nvv

P

Where ^{Re n Inv} is delivered power to inverter and ^{n inv} is efficiency of inverter.

• III.    OPTIMAL SIZING

To select and optimal sizing of a PWHS to satisfy the load demand, the calculations may be carried on the reliability concept and concept of economy of power supply. In this paper the proposed methodology for PWHS calculation is based on two concepts as follow:

• >    Technical concept (Reliability indices like:LOLE, LOLD and LPSP)

• >    Economical concept (PFWHS cost as OCE)

The optimal configuration with the minimum OCE is selected from the set of configurations which satisfy the reliability of power supply.

• A. Reliability Calculation based on Indices Concept

In this paper the applied reliability indices, can be expressed by the following equations [18,19]:

Loss of load expectation can be defined by

N

LOLE = ^ E [ LOL ( t ) ]                     (11)

• t = 1

Where E [LOL] refer to expectation of loss of load which is defined by

E [ LOL ] = ^ T s x P s                          (12)

s e S

Where Tsand Ps refer to duration and probability of load loss respectively.

Loss of Energy Expectation (LOLE) can be expressed by

N

LOEE = EENS = ^ E [ LOE ( t ) ]              ⁽¹³⁾

t = 1

Where E [LOE] is expectation of loss of energy which can be calculated as follows:

E [ LOE ] = ^ Q s x P s                        (14)

s e S

Where Qs is amount of load loss.

The reliability of PFWHS is expressed in terms of loss of power supply probability (LPSP) which is the probability that an insufficient power supply results when the PFWHS is unable to satisfy the load demand.

The LPSP technique is considered to be the technical implemented criteria for sizing. The LPSP of 0 means that the PFWHS power can always fully meet load demand whereas the LPSP of 1 means that the PFWHS power can’t meet the load demand at all. The LPSP can be expressed as:

The net preset-value cost (NPC) for a specific component can be calculated as follow [20,21]:

NPC i = ( N i x CC i + N i x K i x RC i + N i x MRC i x PWA ( ir , R ))

LPSP =

LOEE

N

E D ( t )

t = 1

Where D(t) is load demand (kWh) in time step t. So the reliability of PFWHS can be defined by

Where Ki and PWA(ir,R) are factors that convert replacement costs and operational costs into the net present cost, respectively. The definition of these factors is well presented in [20,21].

The net-present-value cost (NPC) of load loss can be obtained by

Re liability = 1 - LPSP

NPC i_Oss = LOEE x C_{l O}ss x PWA ( ir , R )

So the OCE can be defined as follows:

The Equivalent Loss Factor is calculated by

NQt

ELF =—У

N ^E D t

Where Q (t) is total load loss at step-time t.

B. Expected Generation Energy Calculation of PFWHS

In this section the expected generation energy (EGE) of PWHS is calculated in terms of the outage probability and availability rate of per PWHS components. The expected generation energy of PWHS is defined by

N COM

EGEpFwHs = E (PPFWHS (nCOM )x fiFWHS (nCOM fail nCOM =0

n fail

Where ^COM is the number of components being forced outage of the grid.

Where the failure probability of PWHS can be expressed by

^fPFWS ⁽ nCOM ) = E

^ N COM

fail

V n COM /

( A COM )

N COM nCOM

fail x (1 - Acom ) nCOM

Where, ACOM refers to availability of per PFWHS P      (nfail ) ■

components and ^{PFWHS COM} is power generated by

PFWHS considering failure of components.

C. Economical Calculation based on OCE Concept

In this section the overall cost of energy (OCE) of PWHS takes into account the initial capital cost (CC), maintenance and repair cost (MRC), replacement cost (RC) of components as well as the associated cost to load curtailment during 20 years. The main constraint of problem is the maximum permissible level of the Equivalent Loss Factor (ELF) index.

OCE = ( E NPC i - + NPC oss )

D. Objective Function

The objective function of optimization problem is defined by

OF : Minimize OCE (23)

The objective function should be optimized considering follow constraints:

E [ ELF ] < ELF max

Min (N PV , N HST , N WT ) ≥ 0                        (25)

0 ≤θ PV ≤ 90                                       (26)

IV. PSO ALGORITHM

Particle swarm is a group algorithm in which a set of particles look in problem possible space in order to find an optimum solution of objective function. Each individual moves in search space with adjustable velocity and keeps the best position gained ever in its memory. The best position obtained by all the individuals of the population is transferred between all particles [22-26]. In fact it is supposed that each particle in each moment knows about the best position obtained by all the individuals of the population until that moment. Then the general principles of the algorithm will be explained:

Considering an n-dimensional search space, and a population consisting of N particles, the ith particle is an n-dimensional vector which can be defined by (27) and the corresponding velocity of this particle is also an n-dimensional vector expressed by (28):

^Xi =^[ x i 1 , x i 2 , x i 3 ,..., x in ^{] (27)}

V i = [ v i 1 , v i 2 , ^V i3 ,

...

, V n ]^T

Where i  1,²,3,..., N

In particle swarm optimization algorithm, ith particle saves the best position ever obtained under the name vector   Pi = [pi"pi2,."p-n ] In its memory and

G =[ ^g 1 ,g 2 >-> gn T vector refers to the best position which is ever obtained by all the individuals of the population. th

Position of i particle in (t+1) iteration is defined by the following equations:

V ( t + 1 ) = ^ ( t ) V ( t ) + C 1 ( t ) Г 1 ( P ( t ) - X ( t ) )          ₍₂9)

+ c 2 ( t ) Г , ( ^G ( t )^- X ( t ) )

X ( t + 1 ) = X i ( t ) + X V ( t + 1 ) (30)

In above equation, ^ refers to inertia coefficient which indicates the impact of previous velocity vector on the current iteration. ^X refers to constriction factor which enters to above equations in order to limit velocity vector impact. ^{c 1} and ^{c 2} are cognitive parameter (local acceleration) and social parameter (Global acceleration), respectively. ^{r 1} and ^{r 2} are random numbers, uniformly distributed within the interval [0,1].