Effect of Short-Term Synaptic Plasticity on Correlated firing in Feedback Networks

Published Online June 2011 in MECS

Research in neuroscience has traditionally focused on how neurons communicate. A recent study showed that timing is crucial: the information provided by the sensory neurons is effectively transmitted only during a certain time window [1]. So, the temporal dynamics of neuronal interactions seem to be important for processing the information that goes through the neurons [2,3]. The statistical structure of the population activity could be shaped by diverse measures, which denote the correlated firing in different manners [4-9]. Collective oscillations organize neurons simultaneously into groups for neural information processing, which is a common behavior in neural system [4,6]. Oscillated neurons fire synchronously with similar firing rate, but with different temporal correlation structure. Another observation is that nearby neurons often have correlated response variability in a

+Corresponding author: Jinli Xie wide range of time scales [10-14]. This correlation, typically characterized by the spiking times, interferes with pooling as a strategy to overcome response variability in a population rate coding [2,12].Although correlated response and oscillations have been linked to different views of how information is encoded by neuronal populations, they are functionally and mathematically related [3,10,15]. These two forms of correlations are both believed to arise from common synaptic input and relate to certain connections of network [3,10,11,16]. However, despite the fact that correlation of neurons has been the subject of intense research efforts in many studies, the important role of correlated firing in the brain attracts more attentions [7,17-19].

The transmission of signals between neurons by synapses can vary enormously. At many synapses, pre-synaptic activity dynamically affects synaptic strength [20]. Thus the amplitude of the post-synaptic response is not a static quantity. The recent history of activity at both sides of the synapse can either decrease or increase the efficacy of the synapse. All these changes arise from a large number of mechanisms known collectively as synaptic plasticity, which have a time scale ranging from milliseconds to months [20-22]. On slow timescale (hours or longer) the changes in transmission properties of synapses thought to support learning and memory are referred to as long-term plasticity [20,23]. Whereas, shortterm plasticity, involving changes that last for milliseconds to minutes, provides synapses with computational potential and performs critical implications for the diversity of signaling within neural network [2123]. It is clear that we cannot understand neural coding or information processing without taking synaptic plasticity into account.

The dynamic behavior of short-term plasticity has been explained and modeled in details [20]. Short-term synaptic plasticity of both the facilitation and depression type are commonly seen and are known to involve a variety of biophysical mechanisms [21,22]. The dynamic synapses between excitatory neurons in a recurrent network are demonstrated to play a crucial role in temporal coding and generating synchronization [24]. Pantic et al.[25] have discussed how coincidence detection are affected by a time-varying synaptic strength in a single neuron model. However, the short-term plasticity is generally found in the feedback pathways, which acts to enhance the detection of transient inputs, such as presynaptic bursts and abrupt changes in input rate [23,26]. Marinazzo et al.[27] modeled short-term depression in the feedback network, indicating that dynamic synapses made the network behavior robust for a relatively large range of input characteristics and preserved the temporal and spatial correlation of the input. Here, we will discuss the relationship between the short-term plasticity and the correlations of output spike trains.

In this study, we use a spiking neural network model with global inhibitory feedback loop and correlated Gaussian external stimuli. We start by investigating how feedback strength of the static synapses shapes the correlated firing of the excitatory neurons in the input layer. Several common measures of correlation are employed to study the synaptic effect. Then the short-term synaptic plasticity is added to the feedback loop to determine its contributions to the correlated firing. Based on the changes in synaptic strength during stimulations of presynaptic inputs at different rates, two different types of short-term plasticity are proposed in the simulation. Facilitation leads to increases in synaptic amplitude with increasing input rate, while depression leads to decreases, suggesting high-pass and low-pass filtering, respectively. By analyzing depression alone, or facilitation alone, the measures characterized the correlated firing are discussed with varying synaptic time constants. Moreover, by means of these results we will reveal the roles of the dynamics of depression and facilitation in modulating the firing activity of the feedback networks.

• II.    M odel and M ethod

The basic architecture of our model is described in Fig. 1 [27]. The constant external input S i ( i = 1,..., N E ) drive a population of leaky integrate and fire (LIF) excitatory neurons, which projects to an inhibitory LIF neuron with an effective input current I _f . The output of the inhibitory LIF neuron provides inhibitory synaptic current I _g to all the excitatory neurons.

The dynamics of the membrane potential of the LIF neuron model is described by (1) and a simple spike-and-reset rule: if the membrane potential reaches a firing threshold V _T , the neuron fires and resets to the reset potential V _R .After firing, the neuron is in an absolute refractory state for time T R .

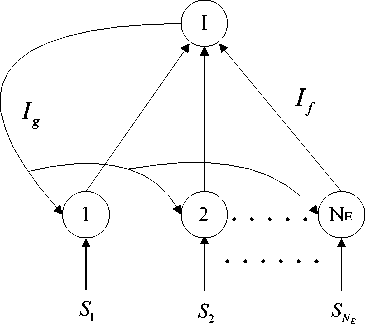
Figure 1. Spiking neural network model with inhibitory feedback.

dV V_R - V I g I

R । g । i dt     T m     C m C m '

where V is the membrane potential, T m is the membrane time constant and C _m is the membrane capacitance. I _i denotes the input current of ith excitatory neuron, which consists of the following components:

I i = _{M e} + G [ -Л-$ ( t ) + _._ ( t )] . (2)

Each excitatory neuron receives a constant base current u _E and a stimulus S i = c _E [ V1 - c ^ i ( t ) + V cd ( t )] with constant power c _E . ^ i is independent for each neuron, while ^ _c is common to all neurons. Both of them represent gaussian fluctuations. The input correlation coefficient c set the relative weight of the shared fluctuations. Identical external stimulus is associated with c = 1 , whereas c = 0 means all external stimulus is uncorrelated among neurons. In (1), I _g denotes the inhibitory feedback current:

I g =- g max G ( t )( E r — V ) , (3)

where, g _max is the maximum synaptic conductance. The minus before the formula mimics the inhibitory effect of the feedback loop. The synaptic current depends on the synaptic conductance and the battery term of the inhibitory neuron. For the case of dynamic synapse, its effective strength is governed by three parameters D , F , G . The variable D denotes the depression, F the synaptic facilitation, and G the synaptic conductance. Their dynamics is given by the following equations between spikes [21, 22]:

dD = 1 - D dt     Td dF - F dt   tf

dG - G dt

^T g

where T d and т f are recovery time constant of synaptic depression and facilitation, respectively. T d is the time constants of synaptic conductance. At every incoming spike from the inhibitory neuron, the depression variable is updated as D ^ Dd . Likewise for facilitation, F is updated as F ^ F + k . F is reset to 0.5 in the next simulation timestep if it reaches higher values than 0.5,. This is important to avoid very high values of F at high frequencies. The synaptic conductance G gets updated according to G ^ G + Dl for depression alone, or G ^ G + Fh for facilitation alone. d , k , g and h are synaptic update rule parameters, which are constant factors. Further, the conductance is updated before or F variables are, because this best mimics the physiological case. With this model, we can easily change to a situation with static synapses by setting G ( t ) = 1 for all t in (3). Here, the strength of the static synapses is equal to g _max .

The input current I _f to the inhibitory neuron due to output of excitatory neurons is given by the convolution of the sum of the spike trains of the excitatory neurons and a delayed a function. The inhibitory neuron also receives a constant base current ^ I .

. „       N E

If=^ ⁺ т ^a ( ^T ) 2 yi ( t ^{- т} ) d ^T ,

,,    t - t d

a ( t ) = —2D exp ^T S

t ^{- T} D ^t s

,

where t d is the transmission delay of the feedforward loop, and t _s is the time constant of synaptic transmission.

The output spike trains of ith excitatory neuron is obtained by collecting the jth instants of threshold crossing with 5 spikes: y(t) = 2 5(t - tj), where tj is the successive firing instants.

The determination of the correlated activity of the neural network model is based on responses to ensembles of stochastic stimuli. Within a particular stimulus category, M trials are recorded for each excitatory neuron, the length of each trial is L . The correlated firing thus can be characterized by the following measures.

• (1)    The mean firing rate describes the intensity of the activity of neurons which is given by the averaged output of the excitatory neurons and equals to the inverse mean interspike interval.

NE M

^ = 22 n- j , i = 1 j = 1 L

where n _{i , j} is the evoked spike count of the ith excitatory neuron to the jth repeated presentation of a particular stimulus.

• (2)    The coefficient of variation (CV) of the spike trains of excitatory neurons measures the dispersion of the probability distribution of interspike intervals, which is defined by the ratio of the standard deviation to the mean:

  CV =

  
  
  

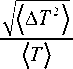
where (a T 2) = {( T - TT ))²} is the variance of interspike intervals of the spike trains of excitatory neurons. For strictly periodic spike train CV = 0 , while poissonian spike train leads to CV = 1 . Thus, a low CV indicates regular spike trains.

• (3)    The power spectrum measures the periodic activity of the excitatory neurons.

S(®) = ( yy * ) ,                 (11)

L y (®) =     e-"t)dt ,          (12)

L ⁰

where y % _i is the Fourier transform of the spike train, y % _i ^* is the complex conjugate of y % _i . A peak can be seen in the power spectrum at finite frequency for the oscillatory neurons. Therefore, the intensity of the oscillations is quantified by the degree of the coherence with the parameters of the peak in the power spectrum:

в= hp" ■ " p a®

,

where ® _p is the frequency of the first peak, h _p is the height and A® is the width at half height of the respective peak.

• (4)    The correlation coefficient of a pair of excitatory neurons can be estimated with minimal statistical error from ratio of the areas of cross-correlation and autocorrelation functions over a time window of length T [1113]. The cross-correlation function of the spike trains of the excitatory neurons is computed as:

  C j ( t ) =

  
  

ML

22 y k ( t ) y k ( t + т ) k = 1 t = 0

M ( L - T ) ^l i X j

where the temporal sum ranges over time bins (i.e. t = 0, A t ,2A t ,..., L ) and M trials when i ^ j . k ‘ is the firing rate of the ith neuron and | L - Ц , as a function of discrete time lag т of the two spike trains, is used to correct for the degree of overlap [12]. The auto-correlation function C _ii of the spike train on each trial is defined by compared with itself. That is, i = j in (7).

All C _ij and C _ii are corrected for correlation induced by the stimulus by subtracting a shift predictor:

SPT j (T ) =

ML

SS y k ( t ) y k ( t + т ) k = 1 t = 0

M ( L - I T )V E^ j

where k' = k + 1( k < M ) or k' = 1( k = M ). SPT ij is used to correct the influence of slow fluctuation in neuronal response in many research studies [11-13]. The pairwise correlation coefficient of neurons i and j is then computed as follow:

R ., ( T ) =

TT

S j ) - S S^pT, ( T )

T =- T          T =- T

, (16)

TT  TT

I [ S C i T ) - S S^pT ,, ( T )][ S C j ( T ) - S S^p T„( T )]

T=-T          T=-T             T=-T          T=-T where T is the window of integration. When T is large enough, Rij is saturated to a steady value. Then the correlation coefficient of the network can be obtained by averaging the pairwise correlation coefficient of all the excitatory neurons:

NN

EE

p=--------E E R ,

N e ( N e - 1)/2 1= 1 j^i + 1 ij

We are considering the subthreshold regime (ц < VT), i.e. the neurons do not fire unless the stimuli are present. In our simulation, we use the following parameter values Vr = 0, Vt = 1, Cm = 1,Tm = 1, c = 0.2, Це = 0.9, о = 0.5 for all excitatory neurons; ц1 = 0.9, td = 4 for inhibitory neuron. Er = 0, d = 0.3, k = 0.1, l = 0.3, h = 0.3 for the R dynamic synapse in the feedback loop; M = 100, L = 11 s for presenting repeated stimulus. The first 1s of every trial is removed to avoid the influence of the initial transient response on the evaluation of the correlated firing.

• III.    R esults

In the static synapses case, the synaptic strength of the feedback loop is constant with varying firing activity of presynaptic neurons. Accordingly, mean firing rate 2 , coefficient of variation CV , degree of coherence в and correlation coefficient p can be plotted as functions of synaptic strength in Fig. 2. 2 decreases monotonously by increasing the strength of the synapses in the feedback loop, owing to the inhibitory effect of the feedback loop on the firing activity of excitatory neurons. Conversely, в is raised when the synaptic strength is increased, indicating the enhancement of the oscillatory activity of the excitatory neurons. However, the curves of CV and p vs. g are non-monotonic. The maximum of CV at max gmax = 0.25 implies the most irregular activity of the excitatory neurons, which is shown by p at a slightly smaller value of gmax ( gmax = 0.2 ). Thus, the correlated minimum is apparent in both coefficient of variation and correlation coefficient, which could be explained by the

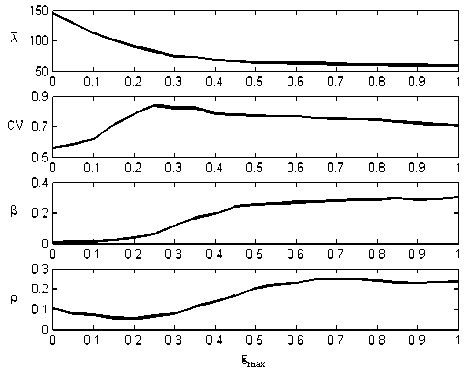
Figure 2. Simulated results for mean firing rate, coefficient of variation, degree of coherence, and correlation coefficient vs. feedback gain for static synapse.

contradictive effects of the inhibitory feedback on correlated firing.

When the synaptic strength of the feedback loop is weak ( g _max <  0.25 ), the mean firing rate of excitatory neurons drops fast with the increasing of synaptic strength (Fig.2), while the degree of coherence keeps in a low level (Fig.2). The firing activity of excitatory neurons shows no oscillations, which becomes lower. The probability of any pairs emitting correlated spikes in a given time window goes down. Thus, an initial tendency of increasing in coefficient of variation and decreasing in correlation coefficient could be seen in Fig.2. In this case, the correlation coefficient decreases in direct proportion to mean firing rate, which is in accordance with the conclusions in Ref. [11]. After the synaptic strength exceeds a threshold ( g _max >  0.25 ), the mean firing rate has fallen to a low level and keeps almost the same with the increase of the synaptic strength (Fig.2). Therefore, the influences of varying of mean firing rate on correlated firing can be omitted. Meanwhile, an increase in synaptic strength leads to the apparent growth in degree of coherence (Fig.2), indicating that the excitatory neurons begin to oscillate periodically. The induced oscillations modulate the regularity of the firing activity of the excitatory neurons. Owing to the oscillations, the discharges in spike trains are periodically correlated with each other. Thereby, the increase of correlation coefficient at large synaptic strength in Fig.2 is mainly due to the effect of the intense oscillations of the excitatory neurons. Although the oscillations of excitatory neurons contribute a little to the coefficient variation, the coefficient variation drops slightly after g _max >  0.25 in Fig.2, providing evidence to the emergence of the correlated activity. Furthermore, with continuous increase of the synaptic strength, the stable and relatively large values of correlation coefficient in Fig.2 reveal that the correlated firing activity is maintained in a high level in the inhibitory feedback network.

Science the firing activity is proved to be sensitive to the strength of synapses in the feedback loop, we then study the effect of short-term synaptic plasticity on the correlated firing by adding depression or facilitation to the feedback loop of the spiking neural network shown in Fig.1. We use gmax = 0.25 in the following simulations. Fig. 3 indicates the synaptic depression and conductance variables (Fig.3 (A)), or the facilitation and conductance variables (Fig.3 (B)) driving by the output spike trains of the inhibitory neuron as functions of the simulation time. We can conclude from Fig.3 that the depression decreases the conductance of synapses, while the facilitation increases the conductance of synapses. The effects of depression and facilitation on correlated firing can be definitely different.

In order to determine how depression and facilitation affect the correlated firing respectively, the synapses in the feedback loop are modeled with either depression or facilitation. By varying the time constants of the synapses, the curves of λ and ρ are compared firstly. λ and ρ as functions of the synaptic time constants are plotted in Fig.4. For depression alone, λ decrease with larger τ _d ’s (solid line in Fig. 4 (A)), while increase with larger τ _g ’s (dashed line in Fig. 4 (A)). For facilitation alone, when τ _d is fixed ( τ _d = 25 ms ), λ is increased with the increasing of τ _f . This is the same case when τ _f is fixed at 10 ms and τ _d is varied. Generally speaking, τ _f and τ _g is beneficial to the improvement of the firing activity, while τ _d can suppress the firing activity. Moreover, when the recovery time constants of synapses are fixed ( τ _d = 25 ms , τ _f = 10 ms ) and the synaptic conductance time constant τ _g is varied, λ reaches higher values with synaptic depression than synaptic facilitation (dashed line in Fig. 4 (A), (B)). Owing to the different effects of these two types of synaptic plasticity on the response amplitude, the mean firing rate in the depressing case is higher than that in the static case (when g _max = 0.25 , λ = 82.5 in Fig.2), and both of them are higher than that in facilitating case.

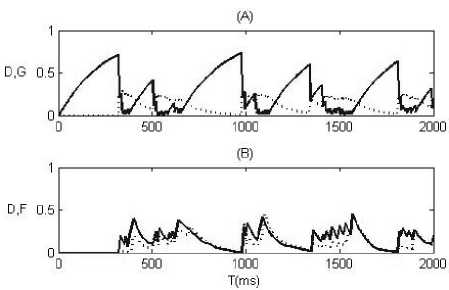
Figure 3. Synaptic depression (solid line) and conductance (dotted line) variables for depression alone (A), or the facilitation (solid line) and conductance (dotted line) variables for facilitation alone (B) as a function of simulation time.

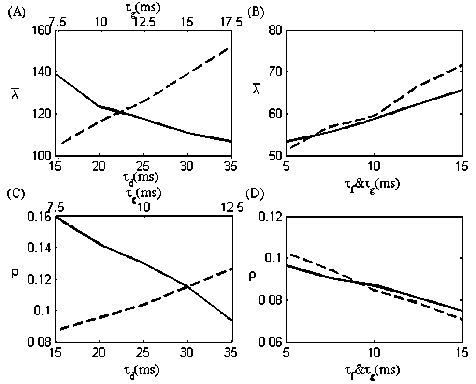
Figure 4. Firing rate (A) and correlation coefficient (C) as functions of τ _d (solid line) and τ _g (dashed line) for depression alone. While varying one time constant, the other is fixed ( τ _d = 25 ms and τ _g = 10 ms respectively). Firing rate (C) and correlation coefficient (D) as functions of τ _f (solid line) and τ _g (dashed line) for facilitation alone. While varying one time constant, the other is fixed ( τ _f = 10 ms and τ _g = 10 ms respectively).

The same trends in the curves of ρ as that of λ are obtained with corresponding parameter regimes (Fig. 4 (C)). Depression decreases the amplitude of the postsynaptic response, leading to weaker strength of the synapses in the feedback loop. Thereby, ρ is larger than that in the static synapse case (when g _max = 0.25 , ρ = 0.0617 in Fig.2) in the whole regimes of τ _d and τ _g . This could be further explained by the curve of ρ in Fig. 2: the correlation coefficient increases when the synaptic strength is smaller than 0.25.

Facilitation leads to stronger synaptic strength, bringing the firing rate down and intense oscillations. In Fig.4(D), ρ varies conversely to λ with the increasing of τ _d and τ _g . Nevertheless, ρ reaches higher values compared to the static synapse case (when g _max = 0.25 , ρ = 0.0617 in Fig.2) in the whole regimes of τ _f and τ _g . The increment in ρ is due to the periodical firing activity induced by strong inhibitory feedback, which has been proved by the nonmonotonic curve in Fig.2. The correlation coefficient increases when the synaptic strength becomes stronger than 0.25.

The curves of CV and β with varying τ _d , τ _f and τ _g are plotted in Fig.5. When τ _g is fixed ( τ _g = 10 ms ), CV and β are increased with increasing τ _d . Conversely, CV and β drop to lower level with increasing τ _g when τ _d is fixed ( τ _d = 25 ms ).When the synapses are depressing, the simulated results of the effects of the synaptic time constants on CV and β appear in opposite way to λ and ρ in Fig.4. Larger recovery time constant of synaptic depression or smaller synaptic conductance

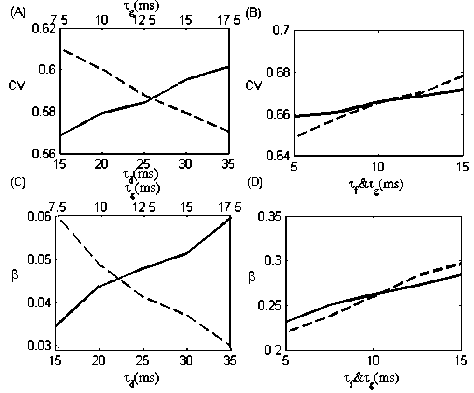
Figure 5. Coefficient of variation (A) and degree of coherence (C) as functions of T d (solid line) and T g (dashed line) for depression alone.

While varying one time constant, the other is fixed ( T d = 25 ms and T g = 10 ms respectively). Coefficient of variation (C) and degree of coherence (D) as functions of t _} (solid line) and T g (dashed line) for facilitation alone. While varying one time constant, the other is fixed ( T _f = 10 ms and T _g = 10 ms respectively).

time constant leads to the decline of the mean firing rate. The firing activity is less correlated, thus the correlations coefficient decreases and the coefficient variation increases. Besides, the slight oscillations are induced by the continuing depression, which cause the increment in degree of coherence.

When the synapses in the feedback loop are facilitating, CV keeps increasing and в keeps decreasing with the increment in both t _f and T g . Larger synaptic facilitation time constant or larger synaptic conductance time constant can lead to the increase of the mean firing rate. However, the intensity of the oscillations is reduced by less effective facilitation in the synapses. The firing activity becomes more irregular by raising T _f and T _g , leading to the increase of the correlation coefficient and degree of coherence and the decrease of coefficient variation. After all, the value of CV with dynamic synaptic keeps smaller than that with static synapses (when g _max = 0.25, CV = 0.8411 in Fig.2).

The simulated results reveal that the correlated firing activity can be modulated by distinct types of short-term synaptic plasticity. By choosing proper synaptic time constants, strictly correlated firing with high level of temporal correlation and periodic properties could be induced in an inhibitory feedback network.

• IV.    C onclusion and D iscussion

In the present paper, we have studied the effect of the strength of synapses in the inhibitory feedback loop on the correlated firing of the feedback spiking neural network. The mean firing rate is decreased, while the degree of coherence is increased with the increment in the synaptic strength. The coefficient variation denoting the irregular of the firing activity first raises to a higher level for small values of synaptic strength, but later drops after synaptic strength keeps increasing. The maximal variation in firing activity is also revealed by the correlation coefficient which measures the correlated firing. The relationship between correlation coefficient and synaptic strength is nonmonotonic. The correlation coefficient trough demonstrates less correlated firing of excitatory neurons with the corresponding values of synaptic strength. Numerical simulation results reveal that there are two contradictive effects of inhibitory feedback on the correlated firing. When the synaptic strength is weak, the inhibitory feedback inhibits the firing rate of the excitatory neurons, thus increases the irregularity of the firing activity. When the synaptic strength is strong enough to induce oscillations of excitatory neurons, the periodic firing activity is beneficial to the enhancement of the correlated firing.

When we add short-term plasticity to the inhibitory feedback loop of the network, depression produces a decrease in synaptic strength, while facilitation produces an enhancement of the synaptic response. Therefore, the mean firing rate is increased with synaptic depression and decreased with synaptic facilitation. However, the correlated measures show complicated characteristics with varying synaptic time constants. The effects of the depression, facilitation and their diverse temporal scales on correlated firing depend on the changes in synaptic strength. If the enhancement of synaptic strength by varying synaptic time constants helps to reduce the firing rate instead of inducing oscillations, the correlation coefficient is decreased and the coefficient variation is increased. If the stronger synaptic strength due to varying synaptic strength leads to intense oscillatory activity of the excitatory neurons, the correlation coefficient is increased and the coefficient variation is decreased. In brief, the correlated firing can be raised not only in depression case but also in facilitation case, no matter how the firing rate changes. The short-term synaptic plasticity in the feedback loop is a flexible way to modulate the firing activity of neural network.

A large array of computations, from temporal and spatial filtering to associative learning could be performed by synapses with plasticity with a wide range of timescales. The short-term plasticity contributes to gain control mechanisms, changes coincidence detection properties and can implement the derivative operation in conjunction with spike frequency adaptation [24,25]. Although a few theories about the functional role of synaptic plasticity have been advanced [20-22], the processes in synaptic transmission are generally not understood. Former studies are mostly interesting in the plasticity interacts with single neuron firing dynamics [22,23]. The fact that our feedback neural network model, based on short-term facilitation and depression, can show the changes in correlated firing providing further evidence for the process contributions of dynamic synapses in population coding. Our study sheds further light on how short-term plasticity interacts to shape response properties, in the context where depression or facilitation are present alone.

A cknowledgements

This work was supported in part by a grant from the National Natural Science Foundation of China (Grant No. 61075105).