Effective Reverse Converter for General Three Moduli Set{(2^n)-1,(2^n)+1,(2^(pn+1))-1}

Published Online September 2012 in MECS

Residue number system is a non-weighted number system which is specified with a muduli set {m 1 ,m 2 ,…,m n } in which an integer number X is represented as (x₁,x₂,…,x_n) that x_i=x mod m_i. Arithmetic operations on residues can be performed in each moduli in parallel without carry propagation between them. The RNS has been widely considered for efficient hardware implementation of digital signal processing (DSP) [3], and for the implementation of high-speed FIR filters [4]. Moreover, RNS has applications in image processing systems, especially RNS image coding which can offer high-speed VLSI implementation of secure image processing algorithms [5].

Because of the carry free property of some operations like addition, subtraction and multiplication, implementation of these operations are easy and fast. Some operations like sign determination, number comparison, and overflow detection cannot be accomplish free of carry between muduli, so they are considered as fundamental problems in RNS. Different solutions are proposed to accomplish these operations. One of them is parity checking where parity means the residue in redundant modulo 2. But this solution is easily to implement only when the dynamic range is odd.

Moduli set selection and reverse conversion design is very significant in RNS. Reverse conversion is mainly implemented with one of the algorithms of Chinese reminder theorem and mixed-radix conversion or a combination of these two.

One of the most popular moduli sets is {2n-1,2n,2n+1}. But today its dynamic range is not sufficient for many applications. So moduli sets with larger dynamic range and sets with more moduli for increasing parallelism are mostly proposed. The modulo 2n looks an appropriate modulo with respect to hardware cost and delay of arithmetic circuits and converters. But this modulo is even therefore the dynamic range will be even, so we would not be able to use parity checking as a solution for the fundamental problems in RNS.

Few moduli sets with odd dynamic ranges were also

-

proposed, like:   {2n-1,2n-3,  2n+3,  2n+1}[6],   {2n-

1,2n+1,22n-2,22n+1-3}[7], {2n-1,2n+1,22n+1} [8], {2n/2

1,2n/2+1,2n+1,22n+1-1}[16]. Because of using 2n-2 and 2n+3 moduli, complexity of internal arithmetic circuits for [6], [7] is high. In comparison to our reverse converter, since in moduli set {2n-1, 2n+1, 22n+1} the third modulo is a multiple of the other moduli, the reverse converter has a better performance. But the arithmetic circuits for moduli in the form of 2n+1 are complex and unfortunately two of them are in this moduli set, so the performance has decreased in the overall RNS. In moduli set {2n/2-1,2n/2+1,2n+1,22n+1-1}, the parallelism is increased but there are unbalance moduli and also two moduli in the form of 2n+1 which lead to decrease in the performance of overall RNS.

In this paper the reverse converter for the general three odd moduli set is proposed based on CRT algorithm in which p is an even number greater than zero. Taking p as a variant we can have the appropriate dynamic range. Therefore, the dynamic range is odd, and consequently the proposed set is amenable to solve difficult RNS problems using parity checking.

In the rest of the paper we will see a brief introduction of RNS (Section II), design of proposed converter for the general case and then for the special case (section III) and at the end of the paper we will review the performance evaluation and finally the conclusion.

• II.    BACKGROUND

A residue number system is defined in terms of relatively prime moduli set {P 1 ,P 2 , …,P n } that is gcd (P i ,P j ) = 1 for i≠j, where gcd (P i ,P j ) denotes the greatest common divisor of P i and P j .

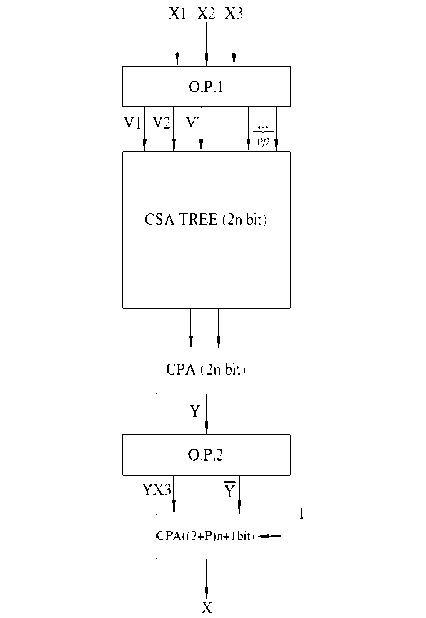
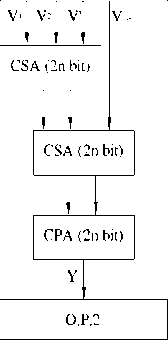
Weighted number X can be represented as X=(x₁,x₂, ... ,x_n), where x i = X mod P i = | X | Pi , 0i

i.

Such a representation is unique for any integer X in the range [0,M-1], where M=P1P2…Pn is the dynamic range of the moduli set {P1,P2, …,Pn}.

The residue number system (RNS) is a carry-free number system which can support parallel and highspeed arithmetic. In this system, a weighted number is converted into a set of small Residues and arithmetic operations can be performed in parallel on each modulo. Since arithmetic operations can be performed without carry propagation between residues, RNS leads to highspeed addition, subtraction and multiplication.

In order to perform some arithmetic operations on a weighted number In an RNS system, a converter is needed to decompose a weighted binary number into a residue represented number, with regard to the moduli set. That converter is a binary to residue converter (forward converter). After forward conversion, arithmetic operations can be performed on each modulo independently and simultaneously and without carry propagation between residues. In order to use the result of arithmetic operations in the form of a weighted number, the resulted RNS number must be converted into its equivalent weighted binary number by residue to binary conversion (reverse conversion).

Binary to residue conversion can be implemented with multi-operand modular adders simply. The arithmetic unit includes modular arithmetic circuits for each modulo channel. Reverse conversion involves a significant degree of complexity.

The algorithms of residue to binary conversion are mainly based on chinese remainder theorem (CRT) and mixed-radix conversion (MRC).

In CRT [1], the residue number (x1,x2,…,xn) with moduli set {m1,m2,…,mn} is obtained as follow:

X =

L

M

M Мш

- =                                                       (2)

Where Mi=M/mi and Ni =|Mi^-1|Pi is the multiplicative inverse of Mi modulo mi for i=1,2,...,l.

By MRC algorithm [1], the residue represented number (x1,x2,…,xn) can be converted into the weighted number X with moduli set {m1,m2,…,mn} as follow:

L

X = a, - Пm_t +... + a_Tm_x + a_x

■=1                                                             (3)

Copyright © 2012 MECS

The cofficients ais can be obtained from the residues by an = (((xn — a1) |m1"1|   — a 2)| m2—11   — ... — an-1) Imn-1-1L mn               mn                        mn mn

Where n>1 and a1=x1.

The RNS has many applications in digital signal processing (DSP) , image processing, RSA algorithm and communication systems. Also, RNS offers new approaches to the design of the error detection and error correction codes. The basic arithmetic components in arithmetic logic unit (ALU) and DSP systems, such as number comparison, parity checking, base extension, sign determination, and overflow detection, turn to a tough obstacle in RNS, which limit many RNS based applications.

Some difficult problems in RNS like number comparison, sign determination, and overflow detection, can be solved based on parity checking. Moreover, parity checking is also one of the fundamental issues for the division and scaling in RNS. For the odd moduli set, the parity checking is one of the fundamental issues [9].

Each RNS system is based on a moduli set which consist of a set of relatively prime integers. The majority of the algorithms for performing these difficult operations are based on reverse conversion. Hence, an efficient design of reverse converter greatly simplify the hardware implementation of these difficult operations.

The complexity of the residue to binary converter and also the speed of the RNS arithmetic circuits are mainly based on the form and the quantity of the moduli in a moduli set.

The most used moduli set is {2n-1, 2n, 2n+1} [10]. The implementation of reverse conversion, modular addition, and multiplication of this moduli set are not complex generally, but number comparison, sign determination, and overflow detection cannot be accomplished based on parity checking because the dynamic range is even. In this case, we would not be able to use parity checking as a solution for the fundamental problems in RNS.

• III.    Design of Reverse Converter

• A.    Design of Reverse Converter for General Three Moduli Set {2ⁿ-1,2ⁿ+1,2^pn+1-1}

For design of the reverse converter we use CRT algorithm. Theorems, properties and lemmas are used in the design.

Theorem1: 2n-1, 2n+1, 2pn+1-1 are pair-wise relatively prime numbers.

Proof: based on Euclid's Theorem gcd(a,b) = gcd(b,a mod b) in which gcd(a,b) represent greater common devisor between a ,b. if a and b are relatively prime to each other, their greater common divisor is equal to one.

gcd(2pn+1-1,2n-1)=gcd(2n-1,1)=1                   (5)

gcd(2pn+1-1,2n+1)=gcd(2n+1,1)=1                 (6)

as 2n-1, 2n+1 are prime relative to 2pn+1-1 and gcd(2n+1, 2n-1)=1, so we can conclude that all three moduli are relatively prime to each other.

Lemma 1: the multiplicative inverse of (2n+1)×(2pn+1-

1) modulo 2n-1 is 2n-1.

Proof: since we have

M =M/m and where N =|M ^-1|P is the multiplicative inverse of Mi modulo mi for i=1,2,...,l.

So for the moduli set we have

X = |x₁ x m₂ x m₃ x M-¹+ x₂ x т^ x m₃ x M-¹+ x₃ x m₁ xm₂xM- ¹|_M                              (14)

Since mT x m2 x M31

= (2²ⁿ- 1) x (-2⁽p^{-2)n +1}

— 2⁽P^-4>+¹-----2^{2n +1}

-2)

2pn+1-1

2n-1

p

2? 2ⁿ -1+1)? ..? 2ⁿ-1+1) -1    = 2-1    =1

2ⁿ-1

2ⁿ-1

pn+1 (p-2)n+1          2n+1        (p-2)n+1      (p-4)n+1            2n+1

-(2pn+1-1)+1=-m +1

With replacing above result in equation (8), we have:

|M^-1x (2ⁿ + 1) x (2?ⁿ⁺¹- 1)|₂n__t = |2^{n- 1}x 2¹ x

1|₂n -1 = |2ⁿ^-i = 1                                   (8)

Lemma 2: the multiplicative inverse of (2n-1)×(2pn+1-1) modulo 2n+1 is 2n-1.

Proof: since p is an even number, we have:

+1 -1

2n+1

p

2? 2ⁿ+1-1)? ..? 2ⁿ+1-1)-1    = 2-1 n =1

2n+1

Replacing above result in equation (10), we have:.

M-1? 2n-1)? 2pn+1-1)     = 2n-1? -21)?       = -2n=1

2                              2n+1                         2n+12

Lemma 3: the multiplicative inverse of (2n-1)×( 2n+1)

_{modulo 2Pn+1-1 is -(2}(p-2)n+1₊₂(p-4)n+1_+...+22n+1_+2).

By substituting the above result in (14), we have:

X = |%1 x m2 x m3 x M-1 + x2 x m1 x m3 x M-1 + x3 x (-m 3 + 1)|M

According to [1], we can consider X as follow:

X = [3xm3 + ^3

[^] = k1 x m2 x M-1 + %2 x m1 x M-1 - X3|mixm2

= x1? 2ⁿ+1)?  ^n-1+x2? 2ⁿ-1)?  ^n-1-x3 2n =

2^n-1(x₁x₁)+2^n-1(2ⁿx₂-x₂)-x₃₂2n_-1= v₁+v₂+v₃+v₄₂2n_-1

With respect to moduli set{2ⁿ-1,2ⁿ+1,2^pn+1-1}, the residues (x1,x2,x3) has representations in binary form as follow:

By substituting above result in equation (11), we have:

^x1 = ^(x1,n -1^x1,n - 2-^X1,0)

-1       n             n                         (p-2)n+1     (p-4)n+1           2n+1              2n

₃           - )               ) _pn+1 (-            -             -...-          - )           - ) _pn+1

^x2 = ^(x2,nx2,n-1^..-^x2,0⁾

pn+1 (p-2)n+1          2n+1        (p-2)n+1      (p-4)n+1            2n+1

...                                                   ...                       pn+1

-(2^pn+1-1)+1₂pn+1_-1=1

^x3   ^(x3,pnx3,pn ^—^t))

Property 1: the multiplication of residue number v by 2P in modulo 2n-1 is equivalent to p bit circular left shifting, where p is a natural number. The proof is mentioned in [1].

Property 2: the negative residue number (-v) in modulo 2ⁿ-1, is equal to the one's complement of v where 0 < v < 2ⁿ-1. The proof is mentioned in [1].

Based on CRT algorithm, the residue number (x1,x2,_,xn) with moduli set {m1,m2,_,mn} , is obtained as follow:

We can write equation (17) in the form of X=Y×m3+x3, in which Y=|v1+v2+v3+v4|2²ⁿ-1.

v = 2^n-1 (x x )

2n

= (x1,0x1,n-1x1,n-2 ...x1,0x1,n-1x1,n-2 ...x1,1 )

22n-1

v₂ = 2^2n-1(0...0x₂)

n-1

n+1

22n-1

= (x 0...0 x x ...x ) 2,0             2,n   2,n-1       2,1

n-1

v₃ = -2^n-1(0...0x₂)

L

X =ZI XNkM

M

n-1

n+1

-1

=(x x   ...x  1...1)

2,n   2,n-1      2,0

n-1

L

M =П m i =1

^v4 ^{= -(x}3,pn^x3,pn-1^...x3,0⁾22n-1 ⁼

^{-2   x}3,pn ^{-2      (x}3,pn-1^...x3,(p-2)n^{) -... -2   (x}3,4n-1^...x3,2n^{) -(x}3,2n-1^...x3,0⁾₂2n_-1

'

v =v +v  =(x  x ...x 1...1) +(1...1x ) =

3       4,1          2,n   2,n-1      2,0                           3,pn n-1           2n-1

(1...1)+(x x   ...x  1...1x ) =(x x ...x 1...1x )

2,n   2,n-1      2,0           3,pn            2,n   2,n-1      2,0           3,pn

2n n+1               n-1                      n+1               n-1

By substituting above result in equation (17), the value of X is calculated as follow in which Yx3 is calculated by concatenation of Y and x3, so we don't need any additional hardware.

X = Y? 2pn+1 -1)+x

X =2pn+1Y-Y+x =Yx +Y+1

Example:

For moduli set {2n-1,2n+1,2pn+1-1}for p=2 and n=3 we have the moduli set {7,9,127}. We calculate X by residue representation (4,4,3) as follow:

x1=4=(100)2

x2=4=(0100)2

x3=3=(0000011)2

With respect to equations 23,24,29,31,33, we have:

v1=(010010)2=18

v2=(000010)2=2

v'=(101111)2=47

v4,2=(111100)2=60

Y=|18+2+47+60|63=|127|63=1

X=128×1-1+3=130

If we consider above results, we can see that the residue representation X=130, with respect to moduli set {7,9,127} is (4,4,3), which is truly calculated.

Hardware architecture of proposed reverse converter is shown in figure 1. For the hardware implementation we use modular adders and logic gates. In this structure the residue number (x1,x2,x3) is changed to ((P/2)+4)-vi vectors by operation preparation1(O.P.1), which is compose of (n+2)-bit not gates. We use a (2n)-bit CSA with EAC tree For calculating Y, in which first module adds the three v1,v2,v' vectors.

Since v2 in equation (24) has n-1bits of "0", so n-1 F.As replace with n-1 H.As. v' in equation (31) contains n-2 bits of "1", so n-2 F.As replace n-2 XNOR/OR pairs. The other vectors also sequentially add with the result of previous module. The worst case is when we need (p/2)+1 addition modules and the best situation is when p/2 is a multiplication of three. In this case the delay will decrease. Here we have considered the worse scenario. The delay of each CSA is equal to the delay of one FA.

In the worst case, CSA tree needs (p/2)+1 CSA modules. Afterwards a (2n)-bit one's complement adder is to be added to the modulo 2n-1, which is a CPA with EAC, therefore its delay is two times of the delay of a CPA that includes a 2n FA modules. In order to calculate the equation (33), we use 2n not gates and at the end, we use a ((2+p)n+1)-bit regular adder.

If we consider the delay of a CSA equal to a FA' delay and the delay of a n-bit CPA equal to an (2n)-bit F.A' delay, the final delay will be calculated as follow: delay=((6+p)n+(2+(p/2))) TFA.

Figure 1. Reverse converter for general moduli set {2n-1,2n+1, 2pn+1-1}

• B.    Reverse Converter Structure for Moduli Set {2ⁿ-1,2ⁿ+1, 2²ⁿ⁺¹-1}

General moduli set {2n-1,2n+1,2pn+1-1}, for p=2 we have moduli set {2n-1,2n+1, 22n+1-1} which is considered as a special case.

X = Y? 22n+1 -1)+x

X=32×1-1+6=37 (34)

2   (x1x1 )       = (x1,0x1,n-1x1,n-2 ...x1,0x1,n-1x1,n-2 ...x1,1 )

^{2n   22n-1}                                              (35)

Example:

For moduli set {2n-1,2n+1,22n+1-1}for n=2 we have the moduli set {3,5,31}. We calculate X by residue representation (1,2,6) as follow:

x1=1=(01)2

x2=2=(010)2

x3=6=(00110)2

With respect to equations above, we have:

v1=(1010)2=10

If we consider above results, we can see that the residue representation X=37, with respect to moduli set {3,5,31} is (1,2,6), which is truly calculated.

XI Х2 ХЗ

X

Figure 2. Reverse converter for moduli set {2n-1,2n+1, 22n+1-1}

v2=(0001)2=1

v'=(1011)2=11

v4,2=(1001)2=9

Y=|10+1+11+9|15=|31|15=1

The delay of this circuit is (8n+3) TFA. Comparing this delay to the same form of moduli sets with the similar dynamic range, will show us that the delay is decreased. The details of the implementation are shown in figure 2.

Table.1 Delay and hardware details of reverse converter for different moduli sets.

• IV.    performance evaluation

Dynamic range of proposed reverse converter for three general moduli set   {2n-1,2n+1,2pn+1-1}   is

((p+2)n+1)-bit and for the special case p=2 is (4n+1)-bit. The reverse converter of this moduli set is comparable to the reverse converters with similar dynamic range. The common and popular odd moduli sets with (4n+1)-bit dynamic range are {2n/2-1,2n/2+1,2n+1,22n+1-1} [16], {2n-1,2n-3,2n+3,2n+1} [6]. In addition {2n-1,2n,22n+1-1} [11], {2n-1,2n,22n-1-1} [12] are two moduli sets with

(4n+1)-bit dynamic range, which are compared to our reverse converter. Hardware implementation details and delay is estimated based on F.A.

Delay is listed in table 1. We can use the unit gate model [13], [15] to estimate the delay and the area. In this model each two input monotonic gate counts as one gate in the area and the delay. An XOR gate counts as two gates in the area and the delay and a F.A counts as seven gates in the area and four gates in the delay. Comparison between the delay and the area of reverse converters in this model are listed in table 2.

According to table 1 our reverse converter has better hardware cost and delay comparing to the reverse converters with moduli sets {2n/2-1,2n/2+1,2n+1,22n+1-1}[16], {2n-1,2n,22n-1-1}[12]. Also it has better hardware cost in comparison with reverse converter with moduli set{2n-1,2n-3,2n+3,2n+1} [6]. According to [1], using memory for large amount of n is not economically feasible for the delay and for the hardware. In addition two unusual moduli 2n-3, 2n+3, will cause decreasing of the performance in the arithmetic unit of RNS system. So from performance point of view our reverse converter is better than the reverse converter in [6] and It has less hardware costs comparing to the reverse converter with moduli set in {2n-1,2n,22n+1-1}  [11], although this module has less delay.

Table.2 Area and delay of unit gate of reverse converter for different moduli sets.

There are some important parameters in designing an RNS like speed of internal RNS arithmetic processing. For estimating this parameter we use the method of [15] in which the time-performance is compared between Copyright © 2012 MECS moduli sets. The speed of arithmetic calculation for a moduli set is determined with slowest modulo which is the critical modulo. We use the unit gate delay of parallel prefix adder for critical modulo of moduli sets of table 1, and the results are shown in table 3. The moduli set {2n-1,2n+1,22n+1}[8], with (4n)-bit odd dynamic range, with respect to table 1 has better delay and hardware cost comparing to our reverse converter with 4n+1-bit dynamic range. however, because of two moduli in form of 2n+1 we will have a decrease in performance of RNS arithmetic unit. So timeperformance of our reverse converter is better than it. So we can conclude that the proposed reverse converter in this paper is better than the other reverse converter with similar dynamic range.

Table.3 Comparison between time-performance of different moduli sets.

• V.    conclusion

In this paper a general three moduli set for even p and it's reverse converter is proposed. This moduli set with ((2+p)n+1)-bit variant dynamic range can have different dynamic range according to different applications. The odd moduli set leads to efficient implementation of internal circuits for fundamental problems in RNS arithmetic and in overall RNS system. The reverse converter in this paper has a better performance in hardware cost and delay comparing to the other reverse converters with similar dynamic range.