Efficient FPGA Hardware Implementation of Secure Hash Function SHA-2

Published Online December 2014 in MECS DOI: 10.5815/ijcnis.2015.01.02

• I.    Introduction

  The SHA-2 was finalized in 2009 by the National Institute of Standards and Technology (NIST) [1]. The SHA-2 algorithm replaced the SHA-1, which had been in use since 1995. Until now, many architectures, for efficient VLSI realization of SHA-2 algorithm, have been proposed and their performance have been evaluated by using ASIC libraries and FPGA [2-11].

Cryptographic algorithm SHA-2 is currently used in a very large variety of scenarios. The most common examples: e-commerce and financial transactions, which have strong security requirements. Thus, the necessity to protect the hardware implementation against the Cryptographic attacks [12-14].

In this paper, we propose a reconfigurable design for the SHA-256 and SHA-512 algorithms. We present its details implementation. Experimental synthesis results show that the proposed architecture achieves a high performance in term of area, frequency and throughput.

The organization of this paper is as follows. Section II describes the related background knowledge. Section III presents describes the SHA-256 and SHA-512 algorithms. Section IV presents the proposed a reconfigurable design for the SHA-256 and SHA-512 algorithms. Their experimental synthesis results and performances are discussed and compared in terms of area, frequency, throughput and efficiency are presented in section V. Section VI concludes the paper.

• II.    Background

Some descriptions of SHA-1, SHA-256 and SHA-512 algorithms can be found in the official NIST standard [1]. Table 1 shows a comparative study of three hash functions characteristics. The security of these hash functions is controlled by the size of their outputs, referred to as hash values. All functions have a similar internal structure and process each message block using multiple rounds. These hash functions enable the determination of a message’s integrity: any change to the message will result in a different produced message digest, with a very high probability.

Table 1: Functional characteristics of two family hash functions

Hash Function	SHA-1	SHA-2
		SHA-256	SHA-512
Size of hash value (n)	160	256	512
Message size	264	264	2128
Message block size (m)	512	512	1024
Word size	32	32	64
Numbers of words	5	8	8
Digest rounds number	80	64	80

• III.    SHA-2 Description

• A.    General

SHA-256 accepts messages with arbitrary lengths up to 264-bit. The SHA-256 Hash function produces a final digest message of 256 bits that is dependent of the input message, composed by multiple blocks of 512-bit each. This input block is expanded and fed to the 64 cycles of the SHA-256 function in words of 32-bit each (denoted by Kt,Wt). Intermediate hash values are rerouted back into the compression loop.

• B.    SHA-256 Description

  • B.1.    Preprocessing

As with other popular hashing functions, with SHA-256 the message to be hashed is first padded so that its final length is a multiple of 512-bit. The n-bit message is padded so that a single 1-bit is added into the end of the message. Then, 0 bits are added until the length of the message is congruent to 448 modulo 512. A 64-bit representation of n is appended to the result of the padding. Thus, the result message is a multiplicity of 512-bit. This message is denoted here as M(i). M(i) message blocks are passed individually to the message expander. Padding can be represented as:

l-bits k-bits           64-bits

Message M

1

000000…0

Value of l

N*512-bits

Fig. 1: Message preprocessing (SHA-256)

• B.2.    Definitions

In the SHA-256 algorithm, six logical functions which operate on 32-bit values are used:

Ch (x, y ,z) = (x ^ y) ⊕ (∼ x ^ y)(1)

Maj(x, y, z) = (x ^ y) ⊕ (x ^ z) ⊕ (y ^ z)(2)

∑0(x) = ROTR2(x) ⊕ ROTR13(x) ⊕ ROTR22(x)(3)

∑1(x) = ROTR6(x) ⊕ ROTR11(x) ⊕ ROTR25(x)(4)

σ0(x) = ROTR7(x) ⊕ ROTR1 (x) ⊕ SHR3(x)(5)

σ1(x) = ROTR17(x) ⊕ ROTR19 (x) ⊕ SHR10(x)(6)

Where ^, ∼ and ⊕ are the bitwise AND, NOT and XOR operations.

ROTR and SHR are the rotate right and shift right functions respectively.

• B.3.    Algorithm

The message, M is expended by a message Scheduler according to the following function:

For j = 0 to 15: W = M j ⁽ⁱ⁾ and

For J = 16 to 63{

W j ← σ 1 (W j-2 ) + W j-7 + σ 0 (W j-15 ) + W j-16 }

For i=1 to N

{Initialize registers a, b, c, d, e, f, g, h with the (i-1)st intermediate hash value.

Apply the following compression function to registers a-h:

For j= 0 to 63{

T 1 ← h+∑ 1 (e)+Ch(a, b, c)+K j + W j

T 2 ← ∑ 0 (a) + Maj(a, b, c)

h ← g ,  g ← f,  f ← e,  e ← d+T 1

d←c,  c←a,  b←a,  a←T1+T2} ith intermediate hash:

H 1 ⁽ⁱ⁾ ← a+H 1 ^(i-1),…,H 8 ⁽ⁱ⁾ ← h+H 8 ^(i-1)}

The hash of M: H^(N) =(H 1 ^(N), H 2 ^(N),…, H 8 ^(N)) [1]

• C.    SHA-512 Description

In this section, the architecture SHA-512 is described. Internal structures of these units and sizes of their operands differ in the four versions of SHA-2.

Full descriptions of the SHA-224, -256, -384 and -512 algorithms can be found in the official NIST standard [1]. SHA-512 produces a 512-bit message hash; SHA-384 a 384-bit message hash etc. An overview of SHA-512 is given here, and then the differences between SHA-512 and the other members of the SHA-2 family are outlined. The SHA-512 algorithm essentially consists of 3 stages:

• -   Message padding unit

• -   Block expansion

• -   Round computation unit.

C.1. Preprocessing

The SHA-2 input block size depends on the algorithm used. The input block size is 1024-bit. The pre-processing stage first splits the original message into N blocks, namely M(1), M(2), …,M(N). Each block has 1024 bits. Then, if the message length is not a multiple of the underlying block size, message padding must be performed. Next, eight initial hash values, H ⁽⁰⁾ ,..., H ^{(0) ,} are set as listed in the specifications [1]. Each algorithm uses a distinct set of initial hash values. (See Fig.2).

l-bits

k-bits

Message M

000000…0

128-bits

Value of l

N*1024-bits

Fig. 2: Message preprocessing (SHA-512)

C.2. Hash Computation

The hash computation is based on operations over 1024-bit words. The number of iterations performed by the algorithm is given by j = 80. Actually, j can be considered to represent the number of 1024-bit words processed by the algorithm. More specially, the SHA-512 algorithms comprise j message schedule words

(W₀,…,W₈₀), eight working variables (a, b, c, d, e, f, g, h), and eight intermediate hash values ( H ^{( i )} ,..., H ₇ ^{( i )} ). As specified in [15],  SHA-512 utilize 80 constants

(K 0 ,…,K 80 ), where each of them is 1024-bit wide. Additionally, six logical functions are employed, as shown below. ROR n(x) and SHR n(x) correspond to, respectively, a rotation and a shift of x by n bits to the right. Besides, ф represents the bitwise XOR operation, ^л the bitwise AND operation, and ~ x the bitwise complement of x.

SHA-512: The hash computation step uses four logical functions: Ch, Maj, Σ0, and Σ1. The result of each new function is either a new 64-bit:

Ch(x, y, z) = (x л y) ф (~x л y)(7)

Maj(x,y,z) = (хЛу) ф (xЛz) ф (zЛy)(8)

G0(x) = ROTR1(x) ф ROTR8(x) ф SHR7(x)(9)

G1(x) = ROTR19 (x) ф ROTR61(x) ф SHR6(x)(1o)

20 = ROTR2(x) ф ROTR34 ф ROTR39 (x)(11)

21 = ROTR14(x) ф ROTR18 ф ROTR41(x)(12)

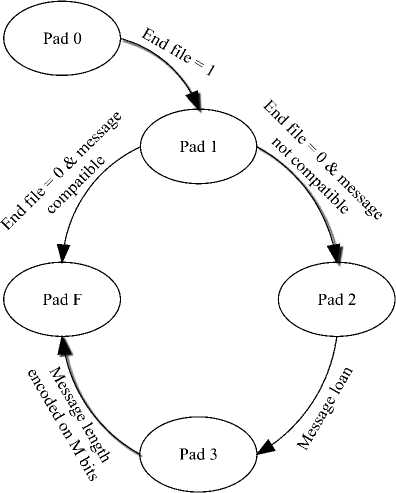
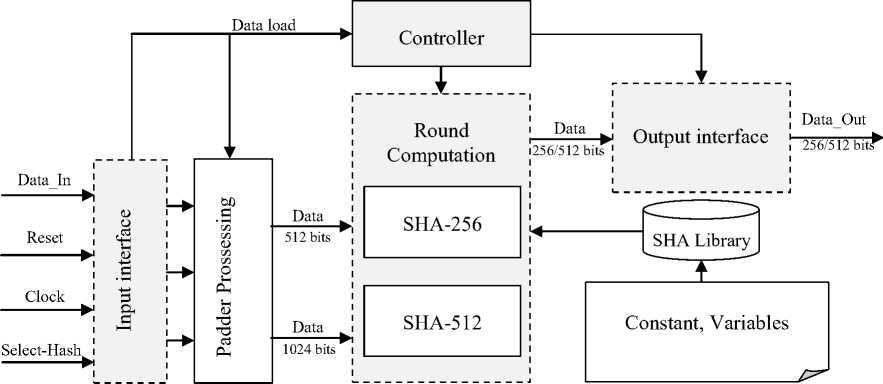
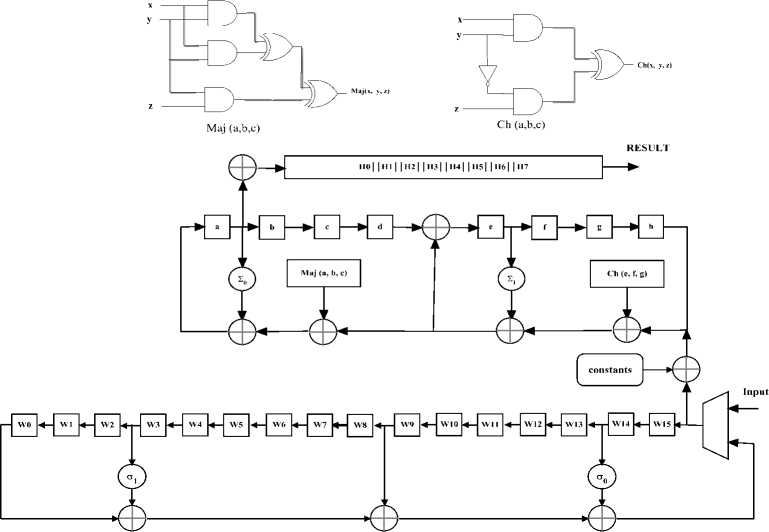
For each message block i, 1< i

• •    Initialize the eight working variables:

a = H(i^-1), b = H(i^-1), c = H (i^-1), d = H< i^-1)

e = H (i^-1), f = H < i^-1), g = H (i^-1), h = H(i i^-1)

• •    Prepare the message schedule:

W = ; Mo^(1-1); 0 < j < 15                             (13)

Wj = ROTL₁ (W_j-3ф W_j-8ф W_j-14ф W_j-16);        (14)

• 16< j < 79

• •    The SHA-512 algorithm is given in listing 1.

Fort = 0 to 79:

{

T = h + 2256 (e) + Ch (e, f, g) + K²⁵⁶ + Wj

T₂ = 205⁶( a) + Maj (a, b, c)

h = g g = f f = e e = d + T1

d = c c = b b = a a = T1 + T2

}

Listing 1. SHA-512 algorithm

• •    Compute the ith intermediate hash value H⁽ⁱ⁾:

H(i) = a + H(i^-1), H(i) = b + H(i^-1),

H (i) = c + H(i^-1), H(i) = d + H(i^-1),

H(i) = e + H(i^-1), H(i) = f + H(i^-1),

H(i) = g + H(i^-1), H(i) = h + H(i^-1),

After all N blocks of message M are processed, the final message digest is obtained by concatenating the hash values ( ) More precisely, the message digest for each algorithm is given by the concatenations shown below. The concatenation of words is represented by the symibN¹ ||H1^(N)|| H2⁽ⁿ⁾ || H3^(N)|| H4^(N)|| H5^(N)|| Ho^(N) [1]

• IV. Proposed Design

This section presents the proposed reconfigurable SHA-256 and SHA-512 design. Fig. 3 shows the block diagram of our reconfigurable AES. The given architecture supports four operation modes for reconfigurable SHA processor.

• •    Input interface and output interface: the input data is arbitrary length, but the outputs are 256 or 512 bits for SHA-256 and SHA-512, respectively. So input interface and output interface have to buffer the input and output data during the loading process.

• •    The Control Unit is designed to control the flow of data in the design, as well as data exchange between the Padded procedure Unit and Hash Computation Unit.

Fig. 4: Finite State Machine of the Padded process unit

Fig. 3: Block Diagram of SHA-256 and SHA-512

The Hash Computation Unit is the principal data path component of the system architecture. SHA-256 requires 64 cycles to produce the 256-bit message digests, however, the SHA-512 performs 80 cycles to produce 512-bit. Each cycle of SHA-512 algorithm requires the previous rounds, as well as the constant value Ki, the core utilize eight 64-bit words: a-d, wish are initialized to predefined values, at the start of each call to the hash function. The padder receives its input words via the Data-in, and the hash value can be read on port Data-out.

Padded Process Unit pads the input data messages and converts them to 1024-bit realizes the message pre-processing, handling all message data to be hashed. A Finite state machine (FSM) is used for this function (See Fig. 4).

The FSM performs the five states

• •    Pad 0: in which data recovery takes place in the form of packets of 8 bits each.

• •    Pad 1 and Pad F: in the course of this transmission a 512 bits a packet counting takes place followed by a compatibility checking

• •    Pad 2: this state consists in finding out the number of bits ‘0’ to be added.

• •    Pad 3: at this level the last packet is loaded up by the binary coding length of the message.

  

  Fig. 5: Proposed compressor scheme

  
  

  CLK

  
  
  
  
  

  Cycle

  
  
  

  Bloc 1 extended and procrssing

  
  

  ^^^^№1111111111

Bloc 2 extended     Bloc 3 extended and procrssing     and procrssing

START

Fig. 6: Timing diagram for hashing process sequence

Several hardware-based SHA-512 designs have appeared in the literature [7-8]. The longest data path (critical path) in the SHA-512 core is the calculation of working variable A, which involves addition modulo264 for SHA-512 of 7 operands (see listing 1). The following techniques have been proposed to speed up calculations in the SHA-512 core.

The constants memory provides the initialization values for the working variables (a,…, h). Initial hashes (H0,…, H7) are also set within this period of time. The initialization of working variables and initial hashes takes one clock cycle.

When initialization is complete, the compressor employs registers a,…, h, as well as Wj and Kjto determine the new values of a,…,h. As described in Step 3 of SHA-2, the algorithm takes j iterations and is controlled internally by an iteration counter. Precisely, SHA-512 utilizes 80 iterations. In each of these iterations, registers W0,…, W15 and a,…,h are shifted in the direction of the arrows shown in Fig. 5. After j iterations, the intermediate hash computation is performed. It would be possible to execute this operation in a single clock cycle. In order to save implementation area, only two adders are utilized.

Fig. 6 shows the first message blocks of N words being stored into the core. The START signal is asserted at the start of each message. The SHA-2 processor is ready to accept data when START is asserted. Each Nb-bit word (Nb = 16) is clocked into the core on the rising edge of CLK when START is asserted. The START signal is used to acknowledge a data request from the core. The end of the message is indicated by a low-state of the START signal. After a feeding of a block of N words at the input, the signal GO is asserted as the SHA-2 core which computes the message digest. After, the next N/2 clock cycles (N = 64 for SHA-256, N = 80 for SHA-512), the message digest for the previous N word block is computed. Finally when the final message block has been processed, the hash value outputs are concatenated to produce the 256 or 512-bit message digest.

• V.    FPGA Implementation

The SHA-256 and SHA-512 have been described using VHDL and simulated by ModelSim 6.6 and synthesized, placed, and routed with Xilinx ISE 10.1.03. The FPGA target was XC5VFX70T from Xilinx Virtex-5 family. The architecture was simulated for verification of the correct functionality, by using the test vectors provided by the SHA-512 standard [1].

As seen in table 2, the number of occupied slices, the frequency (in megahertz), the throughput (in megabits per second) and the efficiency (in Gegabits per second/slices) for the SHA-256 and SHA-512 are presented.

The throughput is computed as:

,      # bit x frequency

Throughput =-----—----- (15)

#clock cycles

The Efficiency is obtained by using the following equation:

Throughput

Efficiency =-----------

Area

Table 2: FPGA implementation of the proposed design: Results

SHA Algorithm	Area (slice)	Frequency (MHz)	Throughput (Gbps)	Efficiency (Mbps/Slices)
SHA-256	387	202.54	1.58	4.19
SHA-512	874	176.06	2.20	2.58

The implementation of the SHA-256 takes 387 slices for 202.54 MHz frequency. The SHA-512 occupies 874 slices for 176.06 MHz Frequency. The number of slices for the SHA-512 is more than that of the SHA-256. This is mainly because of the constants, variables and logical operations are more complex than SHA-512.

Table 3 shows a comparison between our proposed design with some previous works for FPGA implementation.

Table 3: FPGA implementation of the proposed SHA-256: Comparison

SHA Algorith m	Area (slice)	Frequency (MHz)	Throughput (Gbps)	Efficiency (Mbps/Slice s)
Proposed	387	202.54	1.58	4.19
[5]	424	179.5	1.4	3.38
[9]	-	80	0.61	-

Compared to [5] and [9], our proposed design has the minimum area and the highest frequency and throughput. In terms of hardware resources, the proposed design takes 387 slices for 202.54 MHz frequency while the SHA-256 in [5] occupied 424 slices with 179.5 MHz operating frequency. This means that the proposed SHA-256 is the most efficient.

• VI.    Conclusions

In this paper, we proposed a new design for the SHA-256 and SHA-512 functions. Moreover, the proposed design has been implemented on Xilinx Virtex-5 FPGA. Its area, frequency, throughput and Efficiency have been compared and it is shown that the proposed design outperform the previously reported ones.