Efficient Hand off using Fuzzy and Simulated Annealing

Fuzzy logic (FL) can be a valid approach to solving control problems in a wide range of applications. In particular, embedded architectures are likely to use fuzzy logic in the future for dedicated applications. Even if fuzzy logic can be implemented on a general-purpose computer, its application in embedded architectures requires dedicated hardware solutions. Specialized hardware can save costs by implementing only the particular features of the application and, at the same time, can benefit from the application characteristics for speeding up the computation. From this perspective, several architectures have been designed, some fully dedicated to fuzzy computation and others, though showing general purpose characteristics, have a dedicated support to fuzzy logic.

In Hand off mechanism, Signal strength based measurements are considered due to its simplicity. The conventional handoff decision compares the Received signal strength (RSS) from the serving base station with that from one of the target base station, using a constant handoff threshold (also called handoff margin). However the fluctuations in signal strength, causes ping pong effect. Some of the main signal strength measurement used to support handoff decisions are: Relative signal strength, Relative signal strength with threshold, Relative signal strength with hysteresis, Relative signal strength with threshold and hysteresis. The conventional RSS based handoff method selects the Base station (BS) with strongest received signal at all times[1][2]. This method is observed many unnecessary handoffs even when the signal strength of the current BS is still at an acceptable level, which results poor quality of service (QOS) of the whole system.

There are a variety of different ways of implementing a fuzzy inference engine. The software oriented approach in which the inference engine is coded in a software program that runs on a generalpurpose computer is flexible but lacks speed. The hardware-oriented approach in which the inference engine is mapped onto dedicated hardware allows much faster operation but lacks flexibility. As well, there are compromise approaches in which some dedicated units are incorporated into otherwise generalpurpose computer architecture to allow higher-speed operation while at the same time retaining much of the flexibility of a general-purpose computer approach. The advent of high density field programmable gate arrays (FPGA) makes it possible to design dedicated-hardware fuzzy-inference engines relatively easy, and with a high degree of flexibility. A typical rule-based fuzzy controller often requires some amount of tuning, and there are various techniques to automate this tuning process [3]. In this work, the simulated annealing (SA) technique, which is a probabilistic search approach, is employed as the self-tuning mechanism for the membership functions associated with the fuzzy rules. This paper presents an FPGA implementation of a self-tuned fuzzy controller hand off which integrates an earlier FPGA design of a fuzzy controller with an SA-tuning mechanism, on the same FPGA device.

• II.    SELF TUNED FUZZY CONTROLLER

The block diagram of a closed-loop SA-tuned fuzzy control arrangement is shown in Fig.

• 1 .Essentially, there are two major parts in the SA tuned fuzzy controller shown:

• (i)    A fuzzy logic controller

• (ii)    An SA-tuning mechanism

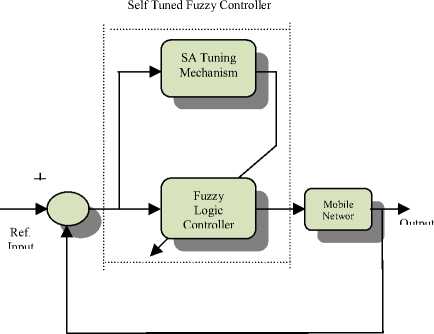
Figure 1: A Self-Tunned fuzzy control with closed loop.

A. Controller

In this case, we consider a 2-input single output fuzzy controller, and the Takagi-Sugeno approach, because it presents the hardware simplicity and the control efficiency. The third part ( defuzzification ) in figure 2 is used to compute the output decision which is combined with the inference for this approach. Its programmability is tied to the possibility of changing the main control parameters (Memberships function, Rules definition). The design of programmable fuzzy controllers is mainly based on the two step:

• B.    Fuzzification

Fuzzy logic is based on the concepts of linguistic variables and fuzzy sets. A fuzzy set in a universe of discourse U is characterized by a membership function mf which assumes values in the interval [0,1]. A fuzzy set F is represented as a set of ordered pairs, each made up of a generic element u Є U and its degree of membership mf(u).A linguistic variable x in a Universe of Discourse U is characterized by a set W(x) = (Wx₁,…, Wx₅) and a set M(x) = (Mx₁,…, Mx₅) where W(x) is the term-set, i.e., the set of names the linguistic variable x can assume, and Wx i is a fuzzy set whose membership function is Mx i . If for instance, x i indicates a temperature, W(x) could be the set W(x)=(low, medium, high), each element of which is associated with a membership function. The membership functions of the fuzzy sets for xi inputs (8 bytes), that we make use in our application is of Gaussian, which is represented in figure 2.

• C.    Inferences

The rules governing a fuzzy system are often written using linguistic expressions which formalize the empirical rules by means of which a human operator is able to describe the process in question using his own experience. If x and y are taken to be two linguistic variables, fuzzy logic allows these variables to be related by means of fuzzy conditional rules of the following type: IF (x is A) THEN (y is B) Where (x is A) is the premise of the rule, while (y is B) is the conclusion[4]. The premise defines the conditions in which the conclusions define the actions to be taken when the conditions of the premise are satisfied. More specifically, the degree of membership of the premise is calculated and through application of a fuzzy logic inference method to the conclusion, it allows the output y to be determined.

In general in a fuzzy conditional rule ''If premise THEN conclusion is made up of a statement in which fuzzy predicates P j of the general form ( X j is A j ) are combined by different operators such as the fuzzy operators AND and OR. In this case X j is a linguistic variable defined in the Universe of the Discourse and A j is one of the names of the term set of X j .

The following is an example of fuzzy conditional rule using operators:

IF P 1 AND P 2 THEN P 4

Where P 1 = (X 1 is A 1 ), P 2 = (X 2 is A 2 ),P 4 =(Y 4 is B 4 ).

To apply an inference method to the conclusion, it is first necessary to access the degree of membership of the premise, through assessment of the degree of membership of each predicate P j in the premise. To used this notion, we are defined this rules by the term a(x,y) with x varies from 1 to 5 and y varies from 1 to 5.

• D.    Simulated Annealing

Simulated annealing (SA) is a generic probabilistic metaheuristic for the global optimization problem of locating a good approximation to the global optimum of a given function in a large search space. It is often used when the search space is discrete (e.g., all tours that visit a given set of cities). For certain problems, simulated annealing may be more efficient than exhaustive enumeration provided that the goal is merely to find an acceptably good solution in a fixed amount of time, rather than the best possible solution. The name and inspiration come from annealing in metallurgy, a technique involving heating and controlled cooling of a material to increase the size of its crystals and reduce their defects. The heat causes the atoms to become unstuck from their initial positions (a local minimum of the internal energy) and wander randomly through states of higher energy; the slow cooling gives them more chances of finding configurations with lower internal energy than the initial one.

By analogy with this physical process, each step of the SA algorithm attempts to replace the current solution by a random solution (chosen according to a candidate distribution, often constructed to sample from solutions near the current solution)[5]. The new solution may then be accepted with a probability that depends both on the difference between the corresponding function values and also on a global parameter T (called the temperature), that is gradually decreased during the process. The dependency is such that the choice between the previous and current solution is almost random when T is large, but increasingly selects the better or "downhill" solution (for a minimization problem) as T goes to zero. The allowance for "uphill" moves potentially saves the method from becoming stuck at local optima—which are the bane of greedier methods.

• III. FUZZY BASED HAND OFF

Input

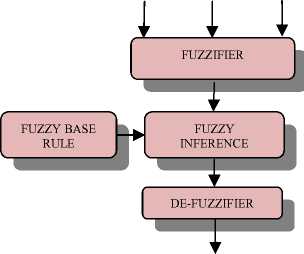
Output Decision

Figure 2: handoff controller based on fuzzy logic.

In order to design a fuzzy logic system the following steps are used in [6]:

• 1.    Identify the inputs and outputs using linguistic variables. In this step we have to define the number of inputs and output terms linguistically.

• 2.    Assign membership functions to the variables. In this step we will assign membership functions to the input and output variables.

• 3.    Build a rule base. In this step we will build a rule base between input and output variables. The rule base in a fuzzy system takes the form of IFAND/OR, THEN with the operations AND, OR, etc.

Network Load

RSS

Distance

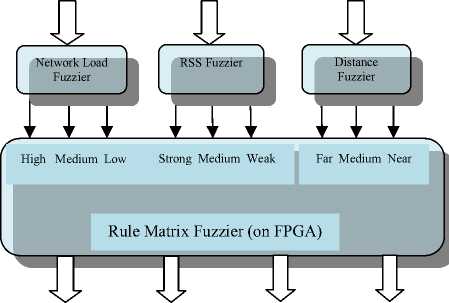
No Handoff          Hold            Caution           Handoff

Figure 3: Fuzzy controller on FPGA.

In this proposed model the range for distance between base station and mobile station is approximately taken 0 to 10 km., the range for received signal strength is taken 0 to 12 mW and the range for network load i.e. number of users in the cell is taken 0 to 20. The membership functions of input parameters for the proposed fuzzy logic controlled handoff mechanism are shown in figure 4, 5 and 6.

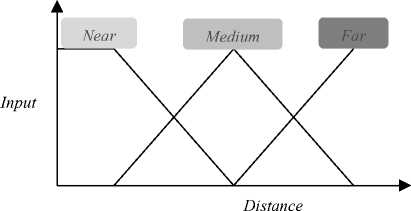
Figure 4 : Membership functions of Distance between BS & MS.

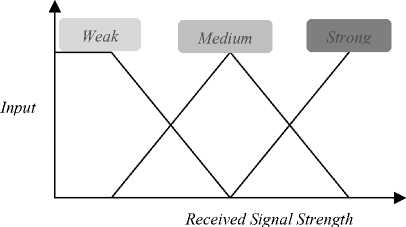
Figure 5: Membership functions of Received Signal Strength (RSS ).

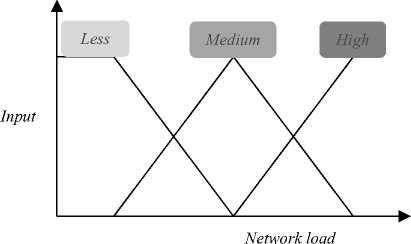
Figure 6: Membership functions of Network Load.

Data to the fuzzy system is first applied to the fuzzifier, which takes the inputs and fuzzifies the information. The fuzzified information is then passed to the fuzzy Inference Engine. The Inference Engine will take the fuzzified input and perform operations on it according to the Fuzzy Rules. These operations will produce output fuzzy sets for each fired rule.

The Output of Inference Engine will be passed to the Defuzzifier. The Defuzzifier will compute a crisp value, i.e., converts the fuzzy domain back to the real world domain. There are several methods for defuzzification such as left max operation, right max operation, center of gravity etc. The Center of Gravity (COG) technique is mostly used method for defuzzification.

• IV .RULE MATRIC FUZZIFIER

Fuzzy logic is an attempt to get the easy design of logic controllers and yet control continuously-varying systems. Basically, a measurement in a fuzzy logic system can be partly true, that is if yes is 1 and no is 0, a fuzzy measurement can be between 0 and 1.The rules of the system are written in natural language and translated into fuzzy logic. For example, the design for a furnace would start with: "If the temperature is too high, reduce the fuel to the furnace. If the temperature is too low, increase the fuel to the furnace.

Measurements from the real world (such as the temperature of a furnace) are converted to values between 0 and 1 by seeing where they fall on a triangle. Usually the tip of the triangle is the maximum possible value which translates to "1."Fuzzy logic, then, modifies Boolean logic to be arithmetical. Usually the "not" operation is "output = 1 - input," the "and" operation is "output = input.1 multiplied by input.2," and "or" is "output = 1 - ((1 - input.1) multiplied by (1 -input.2))". This reduces to Boolean arithmetic if values are restricted to 0 and 1, instead of allowed to range in the unit interval [0, 1]. The last step is to "defuzzify" an output. Basically, the fuzzy calculations make a value between zero and one [7][8][9]. That number is used to select a value on a line whose slope and height converts the fuzzy value to a real-world output number. The number then controls real Handoff.

If the triangles are defined correctly and rules are right then the result is said to be a good control system. When a robust fuzzy design is reduced into a single, quick calculation, it begins to resemble a conventional feedback loop solution and it might appear that the fuzzy design was unnecessary. However, the fuzzy logic paradigm may provide scalability for large control systems where conventional methods become unwieldy or costly to derive.

Fuzzy is an electronic technology that uses fuzzy logic instead of the two-value logic more commonly used in digital electronics. The fuzzy rule base (FRB) for the proposed model for handoff mechanism is shown in Table 1. Total 27 rules are formulated based on the different combinations of the 3 input parameters and 1 output parameter [10].

V . SELF TUNED MECHANISM

The SA algorithm used in the self-tuned fuzzy controller can be described briefly as follows:

(i)An antecedent or consequent MF parameter is chosen and perturbed randomly.

(ii)A cost function, C (w), based on the integral of time and absolute error (ITAE) is used to indicate the performance of the system, that is,

C (w) = f tle(t)ldt ...........(1)

Where w is the parameter vector, T L is the length of the time interval for evaluating the cost function, t is the time, and |e (t)| is the absolute error between the reference input and the output.

Table 1 : Fuzzy Rules for Handoff Controller

Rule no	Distance	Received Signal strength	Network Load	Decision
1	Near	Strong	High	Delay
2	Near	Strong	Medium	Stop
3	Near	Strong	Low	Stop
4	Near	Medium	High	Delay
5	Near	Medium	Medium	Stop
6	Near	Medium	Low	Stop
7	Near	Weak	High	Start
8	Near	Weak	Medium	Stop
9	Near	Weak	Low	Stop
10	Medium	Strong	High	Alert
11	Medium	Strong	Medium	Stop
12	Medium	Strong	Low	Stop
13	Medium	Medium	High	Start
14	Medium	Medium	Medium	Delay
15	Medium	Medium	Low	Stop
16	Medium	Weak	High	Start
17	Medium	Weak	Medium	Alert
18	Medium	Weak	Low	Delay
19	Far	Strong	High	Start
20	Far	Strong	Medium	Alert
21	Far	Strong	Low	Start
22	Far	Medium	High	Stop
23	Far	Medium	Medium	Alert
24	Far	Medium	Low	Delay
25	Far	Weak	High	Start
26	Far	Weak	Medium	Start
27	Far	Weak	Low	Start

• (iii)    According to the Metropolis criterion, the perturbed parameter is accepted as a new starting point if there is an improvement in performance, otherwise, it is accepted probabilistic that leads to degradation in performance. More formally, it is accepted:

• (a)    When there is an improvement in performance, namely,

C (w') < C (w)............ (2)

Or,

• (b)    When there is deterioration in performance, with a probability of

P = e^ (c (w)-c’ (w))/T............. (3)

Where w' is the perturbed parameter vector, p is the probability of acceptance of the perturbed value, and T is a control parameter called the "temperature"[11].

• (iv)    The process is started with a large value of T, which is reduced by a factor of 0.85 each time when the process reaches a "thermal equilibrium". Here, this is assumed to occur after the number of trials is equal to 5 times the total number of MF parameters

• (v)    A near-optimal configuration of MFs results as T=0. The above procedure is carried out after each complete fuzzy control operation, and, as a result the speed of the tuning mechanism is not paramount. The mapping of the SA-algorithm to hardware is based on generalpurpose hardware architecture to reduce the number of logic gates required. A simplified block diagram of the data path of the SA portion of the design is shown in Fig. 7. As can be seen, this is quite similar to some general-purpose microprocessor designs using dedicated functional blocks for various parameters.

The processing unit in the Figure carries out addition, subtraction, division, and multiplication, with the latter two based on shift-and-add or shift and-subtract operations that require 8 clock cycles to complete. The value of the timer is used as one of the operands in the cost function (ITAE) calculation, with the input (the error) forming the other operand. To simply the computation requirement, the exponential function required in Eqn. (3) is provided by a 16-byte look-up table (EXP). The MF parameters and the corresponding perturbed values are stored in the MFs block which also provides storage for the set of the best MF parameters attained so far.

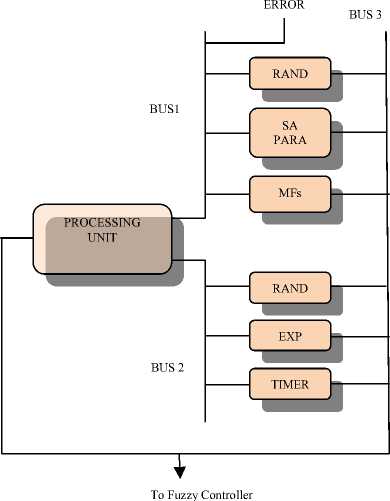
Figure 7: The SA-tuning mechanism data-path.

This set of best MF parameters is used at the beginning of a new temperature value T . Altogether, two 16-byte RAMS are required for the MFs, as shown in Fig. 7.

After each perturbation of a parameter, the perturbed value is transferred to the fuzzy controller through Bus 3 labeled in Fig. 8. Other parameters for the SA procedure are stored in the 16-byte RAM parameter block ( SA PARA). Two pseudo-randomnumber generators (RAND), which are constructed with linear feedback shift registers, are used to determine the amount of parameter perturbation, and for the Metropolis acceptance criterion.

BUS 3

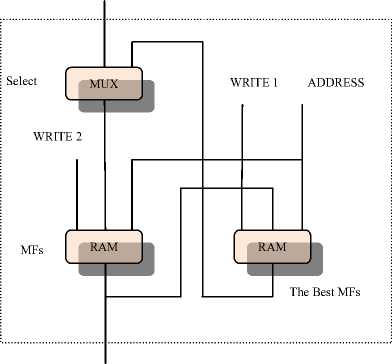
BUS 1

Figure 8: The internal organization of the MFs block.

V.IMPLEMENTATION OF SELF TUNED FUZZY BASED HAND OFF

The application of fuzzy technologies into real time control problems demands the development of efficient hardware implementations of fuzzy inference mechanisms. A Field Programmable Gate Array (FPGA) may be a good solution for it. FPGA is a digital integrated circuit that can be programmed to do any type of digital function [9]. There are three main advantages of an FPGA over a microprocessor chip for fuzzy systems:

• (1)    An FPGA has the ability to be reprogrammed on the site

• (2)    An FPGA used as a fuzzy controller will be semicustom hardware

• (3)    The FPGA will operate faster than a microprocessor chip.

FPGAs are programmed using support software and once they are programmed, they can be disconnected from the computer and will retain their functionality until the power is removed from the chip. A Read Only Memory (ROM) type of a chip that is connected to the FPGA’s programmable inputs can also program the FPGA upon power up. Approximately 3,000 gates are needed to implement the SA-tuning mechanism containing both the data path and the control unit. Another 7,000 gates are required by the fuzzy controller. The 10,000 gates required for the complete SA-tuned fuzzy controller have been implemented on a Xilinx XC3S200 FPGA whose maximum capacity is about 200,000 gates. The system runs on a 50 MHz clock out off 125MHz . During normal fuzzy-control operation, the input (error) value and the timer value are multiplied and accumulated continuously every nine clock cycles to form the cost function. At the end of a complete fuzzy-control operation, the cost value is used in the SA procedure described above to determine whether the current MF configuration is acceptable or not. A new perturbed MF parameter vector is then prepared for the next fuzzy-control operation, and the process is repeated. The evaluation of the Metropolis criterion requires between 23 to 40 clock cycles, whereas the parameter perturbation requires 45 clock cycles. Therefore, a typical SA procedure requires between 70 to 90 clock cycles to complete. An additional 30 cycles are required for temperature scheduling. The functionality of the proposed system is verified from the waveform generated by the simulation tool. The simulation tool used for the simulation is ISE Simulator. The Target device (FPGA) used for implementation of the proposed system is XILINX’s SPARTAN3 XC3S200.

VI.CONCLUSION

An FPGA implementation of an SA-tuned fuzzy controller hand off has been described. The total number of gates required for the controller is about 10,000 , and the Self Tuned Fuzzy Hand off controller has been implemented on a Xilinx XC3S200 FPGA . The evaluation of the Self Tuned Fuzzy Handoff Algorithm requires about 100+9n clock cycles.