Efficient optimum safety factor approach for system reliability-based design optimization with application to composite yarns

When Deterministic Design Optimization (DDO) methods are used, deterministic optimum designs are usually pushed to the design constraint boundary, leaving little or no room for tolerances (or uncertainties) in design, manufacture, and operating processes. So deterministic optimum designs obtained without consideration of uncertainties could lead to unreliable designs, therefore calling for Reliability-Based Design Optimization (RBDO). It is the objective of RBDO to design structures that should be both economic and reliable. However, the coupling between the mechanical modeling, the reliability analyses and the optimization methods leads to very high computational cost and weak convergence stability. To overcome these difficulties, two points of view have been considered. From a reliability view point, RBDO involves the evaluation of probabilistic constraints, which can be executed in two different ways: either using the Reliability Index Approach (RIA) or the Performance Measure Approach (PMA) [1]. The major difficulty lies in the evaluation of the probabilistic constraints, which is prohibitively expensive and even diverges for many applications. However, from an optimization view point, a hybrid method based on simultaneous solution of the reliability and the optimization problem has successfully reduced the computational time problem. However, the hybrid RBDO problem is more complex than that of deterministic design and may not lead to local optima. To overcome both drawbacks, an Optimum Safety Factor (OSF) method has been proposed to compute safety factors satisfying a required reliability level without demanding additional computing cost for the reliability evaluation. The efficiency of the OSF method has been demonstrated relative to the hybrid one for a linear distribution law [2]. In this work, the OSF is reformulated considering RIA and PMA. Next, an extension to multiple failure modes is carried out. Finally, an application on composite yarns is carried out for linear and nonlinear distribution laws and multiple failure modes (scenarios).

The reliability-based design optimization problem is performed by nesting two sub-problems [3, 4]:

• 1:    Optimization problem: The objective is to minimize an objective function f ( x ) subject to deterministic

constraints g k ( x ) <  0 and a required reliability level p ( x,u ) > в t as follows:

min: f ( x )

subject to g k ( x ) <  0 and в ( x,u ) > в _t

2: Reliability problem: The objective is to find the minimum distance between the origin of the normalized space and the MPP (Most Probable failure Point or design point) on the limit state function (Fig. 1). The problem can be written as follows:

в = min

n

d (u )= ^ ui

subject to H ( x,u ) < 0

For more details about reliability analysis, readers can see [5]. These two sub-problems are carried in two different spaces: physical and normalized spaces (Fig. 1).

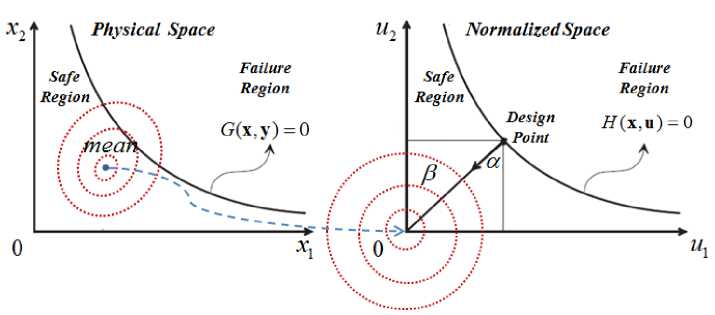
Fig. 1. Physical and normalized spaces [3, 4]

Рис. 1. Физические и нормализованные пространства [3, 4]

These nested problems require a high computing time, however, the Optimum Safety Factor (OSF) is used to solve these numerical difficulties.

• 3.    OSF developments

• 3.1    OSF considering RIA and PMA
  
  3.1.1    OSF based on RIA

The probabilistic constraint in RIA can be evaluated by solving the first-order reliability analysis to calculate the design point P* , which is formulated as an optimization problem with an equality constraint H ( u ) = 0, in the normalized space:

and can be also written as:

min : d(u) u subject to: H(u) = 0

min : d2(u) u subject to: H(u) = 0

The Lagrangian function for the problem (3b) can be written as

L (u, X) = d 2 (u ) + X- H (u)

The optimality conditions for the Lagrangian function are:

d L   d d ² , dH _A

=+ X= 0 d u i    d u i      d u i

i = 1,..., n

— = H (u ) = 0

5X     v 7

Using the expression for the square distance d² in the equation (3b), we get:

xa H

2 5 ui ’

i = 1,..., n

(3a)

(3b)

(5a)

(5b)

The evaluation of the probabilistic constraint in PMA requires an inverse reliability analysis, which corresponds to the inverse problem of the reliability analysis to calculate the design point P* , which is formulated as an optimization problem with an equality constraint d ²(u) = P 2 , in normalized space:

Машиностроение и машиноведение

min :   H (u)

u subject to: d(u) = Pt

(7a)

and can be also written as:

min : H(u) u subject to: d2 (u) = в2

The Lagrangian function for the problem (7b) can be written as

L (u, X, s ) = H (u ) + X-[ d 2 (u )-p 2 ]

The optimality conditions for the Lagrangian function are:

д L   д H , д d ¹  _A

=   + X= 0

д u_i    д u_i      d u i

i = 1,..., n

— = d2 (u ) = 0 дХ      v ’

Using the expression for the square distance d² in the equation (7b), we get:

1 ан 2x5^ ’

i = 1,..., n

(7b)

(9a)

(9b)

According to equations 6 and 10, the resulting normalized vector u can be written in term of the same derivative д H / 6u i .

• 3.2    OSF for component RBDO

Let us consider now the case of n=2 normalized variables i = 1, 2 (see Fig. 2). The tangent of a is given by: tan a = u ₂ / u 1 . Using (6) and (10), we get the same formulations as follows:

dH д u

^tan ' H

д ui

The formulation (11) shows that there is no difference between RIA and PMA for the following OSF developments. The problems (3) and (7) give us the reliability index в as the minimum distance between the limit state surface and the origin [8]. This means that the resulting reliability index may be lower or higher than the target reliability index в t . As we wish to satisfy a required target reliability level for the optimization problem, we can write

n

P 22 = Z u 2 i = 1

Thus, the general expression for the normalized variable u_i when using RIA or PMA, is

ui = ±в t

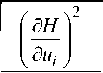
n z j=1

' дh f д u j

i = 1,..., n

The calculation of the normalized gradient д H / д u is not directly accessible because the mechanical analysis is carried out in the physical space rather than in the standard space [9, 10]. However, using theory of statistics, we can derive the following expression from which the computation of the normalized gradient can be carried out by applying the chain rule on the physical gradient д G / д y :

д н   д G ^д T k - ( x,u )

=                         , i = 1,...,n, k = 1,...,K дu i   5yk    д ui

where T-1(x,u) is the inverted probabilistic transformation function. We find that the normalized gradient can be expressed as дн 8g ■ i

=            , i = 1,..., n

д u  дубуi

To summarize, we satisfy the required target reliability index as follows:

n

dP=P t = JZ( u* )•

V i = 1

i = 1,..., n

Thus, we compute the optimum safety factors subject to the optimum values of the normalized variables u_i ^* . According to (13) and (15), it has been demonstrated that the optimum values of u_i ^* can be written in the following form:

*

ui =±P t

д G

8у.

n z j = 1

8 G

⁸ y j

i = 1,..., n

where the sign of ± depends on the sign of the derivative, i.e.:

д G       *         д G

— >  0 о u i >  0 and — <  0

^д У i                       ^д У i

*

о u i <  0   , i = 1,

...

, n

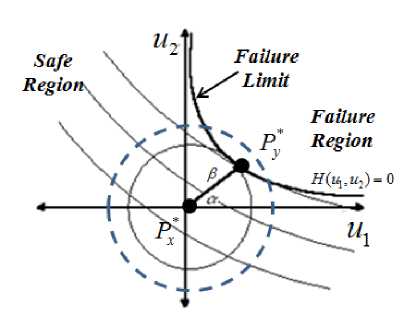
Fig. 2. Design point modeling in a double normalized variable space

Рис. 2. Моделирование точек проектирования в двойном нормализованном переменном пространстве

The efficiency of the OSF is to transfer the reliability problem into an analytical formulation (17). This formulation has been extended to several distribution laws (normal, lognormal, uniform Weibull, and Gumbel laws) for single failure mode cases considering only RIA [11]. However, in this work, both RIA and PMA are used to show the efficiency of the OSF formulation, and an extension to multiple failure case is carried out in the next section.

• 3.3    OSF for system RBDO

The system reliability problem can be written as:

P system = min ^{d (} u i ) = V ^u 12 + ^u 2 + ... + ^u n s.t.: ^H j ( ^u 1 , ^u 2 ,..., ^u m ) ^ ^{0                      (19)}

where d(ui)is the minimum distance between the Most Probable failure Point (MPP) and the optimal solution in the normalized space (Fig. 1). AndHj (ui )< 0 represent the different failure modes. Using similar way, the analytical formulation using OSF for a system RBDO can be written as follows:

Машиностроение и машиноведение

*

u i = ±β t

^m ∂ G j

^∑ j = 1 ^{∂ y i}

n

m

nm

∂ G j ∑ ∑ _{∂ y} i = 1 j = 1 ⁱ

The formulation (20) provides different optimum values of the normalized variables at the failure point and taking into account several failure modes.

• 4.    Numerical Application on composite yarns

Composite materials have been used in structures for centuries. In recent times, composite parts have been used extensively in aircraft structures, automobiles, sporting goods, and many consumer products. Composite materials are those containing more than one bonded material, each with different structural properties. The main advantage of composite materials is the potential for a high ratio of stiffness to weight. To solve the composite yarns structures (or systems), a stress unilateral study is required.

a) Ropes of composite yarns

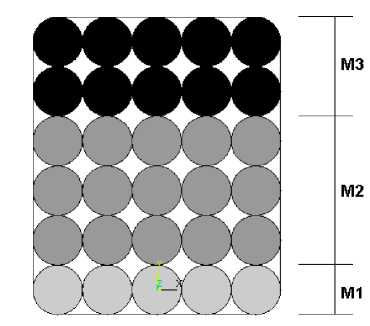
b) Section of the studied rope

Fig. 3. Material structure

Рис. 3. Структура материала

• 4.1    Problem description

• 4.1    Single yarn behavior

For tri-material structure illustrated in Fig. 3, the number of yarns n_i , the section S_i , the Young's modulus E_i , the Poisson's ratio ν _i and material density ρ _i are given according to each material as shown in Table 1.

Table 1

Material properties of different used yarns

Material number ni Si (m2) Ei (Pa) νi ρi (Kg/m3) M1 5 10e-8 5.8e6 0.4 4.0 M2 15 10e-8 8e6 0.3 5.0 M3 10 10e-8 9e6 0.2 6.0

A stress unilateral structure is not capable of transmitting compression, i.e. negative stress: all its internal efforts are traction. The formulation of this problem is complex and may lead to non-existence of solutions or several approximate solutions. Some methods have been developed to determine a solution among all resulting configurations [12].

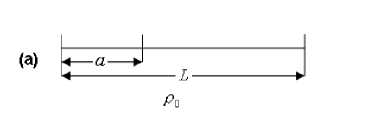
a) Initial case of a yarn and

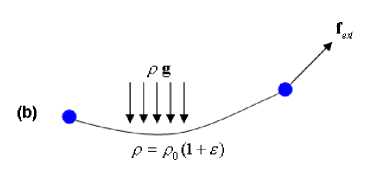
b) Stress case when applying external forces

Fig. 4. The tension on the yarn

Рис. 4. Напряжение действующие на нити пряжи

The behaviour of an elastic file is not defined by the single Hooke’s law; even in the frame of the linear elasticity, we have

т e = — and — > 0                                       (21)

K where K > 0 is the constant of elasticity and T is the tension which defines the internal efforts of the studied yarn. The total section is given by n1n2n3

S = T S1, i + T S2, j +E S3, k(22)

i=1        j=1

and the total tension is given by n1n2n3

T = T —i+T VL —з—(

• i=1        j=1

with

SSS

• — = -i— — , — .= -j— — and — ,= -k— —

1,i     S        2,j     S             3,k

Fig. 4a shows the initial case of a yarn in which the volume mass = p0. When applying an external force and considering the gravity force (see Fig. 4b), the equilibrium vector equation can be written as dT + P0g = 0, da with p = p0(1 + e).

For our studied rope, there is a non gravity force p ₀g = 0 . So, we get

T(L) = fext(25)

This way, the tension is a proportional value of the external force as follows SSS

—1,i =   fex , —2, j = j fx and —3, — = -S- fex(26)

Here, the failure conditions are written as follows:

^e 1, i — ^e 1,max , ^e 2, j — ^e 2,max ^{and e} 3, k — ^e 3,max

In order to compute the maximum strain of each material, we have

^e 1, i

T 1, i

K 1, i

T2,j              T3k e2,j =      and e3,k = y-

K 2, j              K 3, k

DDO procedure:

The optimization problem is to minimize the mass subject to the allowable strain e w and taking a global

safety factor S _f . This optimization problem must be followed by the reliability analysis as follows:

1- Optimization problem

Машиностроение и машиноведение

min mass ( x ) subject to e (x) — e _w =e li_m / S f

• 2-    Reliability analysis

  в = min d ( u ) =

  
  

  n

  Z u 2

  
  

  subject to e (u) < e _lim

  
  
  
  

RBDO procedure

Using OSF method, the RBDO procedure contains three main steps:

subject to e(y) < Elim and for a multiple (double) failure mode as follows:

min       mass ( y )

subject to e (y) <6^                                           (31)

T (У) <  T lim

• 2-    The second step is to compute the optimum safety factors using linear and nonlinear distributions [9] when the number of the deterministic variables is equal to that of the random ones. During the optimization process, we obtain the sensitivity values of the limit state with respect to all variables.

• 3-    The third step is to calculate the optimum solution. This encompasses inclusion of the resulting values of the safety factors into the design variables in order to evaluate the optimum solution.

• 4.4 Numerical results
  
  4.4.1    Component RBDO

According to Table 2, the DDO procedure leads to a high reliability index, while the RBDO one satisfies the required reliability level for the linear and nonlinear distribution laws. The resulting reliability index is: в = 3 that corresponds to a probability of failure (Pf ® 0.1%).

DDO and RBDO results for a single failure mode

Table 2

Parameters	Design Point	Optimum Solution
		DDO	RBDO
		Normal	Normal	Lognormal	Uniform	Weibull
S1	0.2900	0.4400	0.3415	0.3387	0.3413	0.3455
S2	0.4750	0.8500	0.5774	0.5698	0.5655	0.5922
S3	0.5550	1.2300	0.6846	0.6737	0.6632	0.7072
e max	0.0095	0.0048	0.0078	0.0079	0.0080	0.0076
Mass	0.034	0.0669	0.042	0.041	0.041	0.043
в	--	7.8231	3.00	3.00	3.00	3.00
S f 1	--	--	0.849274	0.856135	0.849613	0.839352
S f 2	--	--	0.822641	0.833690	0.839981	0.802099
S f 3	--	--	0.810724	0.823839	0.836908	0.784831

• 4.4.2    System RBDO

• 6.    Conclusions

It is easy to study structures under the most critical mode but it may provide inaccurate results for structural reliability analysis. When dealing with several failure modes, the sensitivity study of each failure mode with respect to all parameters may lead to strange results for the role of certain parameters. The required reliability for both failure modes (tension and strain) is considered to be: в t = 3 that leads to a system reliability index в System > в _t . The system reliability index should be bigger or equal to the minimum required reliability index of all failure modes в System >  min( в j ). Table 3 shows Linear and nonlinear RBDO results for the same target reliability index for both failure modes.

Linear and nonlinear RBDO results for multiple failure modes

Parameters	Design Point	Optimum Solution
		Normal	Lognormal	Uniform	Weibull
S1	0.2900	0.3432	0.3402	0.3421	0.3479
S2	0.4750	0.5774	0.5698	0.5655	0.5922
S3	0.5550	0.6850	0.6740	0.6632	0.7078
ε	0.0095	0.0078	0.0079	0.0080	0.0076
T	66335	58956	59526	59909	57830
Mass	0.0343	0.0418	0.0413	0.0409	0.0430
β system	0.0000	3.0242	3.0242	3.0241	3.0183
S f 1	0.00	0.845081	0.852562	0.847811	0.833615
S f 2	0.00	0.822641	0.833690	0.839981	0.802099
S f 3	0.00	0.810263	0.823460	0.836803	0.784156

Table 3

In this paper, the OSF method is shown as a distinctive tool for RBDO problems. This method is based on the sensitivity of the limit-state function with object of determining the role of each studied parameter relative to the failure mode (or modes). First of all, it has been shown that the idea of the OSF method is to avoid the reliability constraint evaluation with a particular optimization process. In addition to its simplified implementation framework to completely decouple the optimization and the reliability analyses, it provides designers with efficient solutions that should be economic satisfying a required reliability level. The developed equation of OSF basing on both of RIA and PMA leads to the same formulations. The OSF procedure needs only single optimization process for the design point without additional computing time because it has a single variable vector. Finally, the developments based on the reliability view point are less efficient than those based on the optimization view point because the second provides us with reliability-based optimum designs without additional computing cost for probabilistic (reliability) constraints and can lead to global optima. It is shown that the RBDO compared to OSF has several advantages: small number of optimization variables, good convergence stability, small computing time, satisfaction of the required reliability levels. For composite structures, the RBDO problems are more difficult than for simple structures because we deal with several related limit state functions.