Introduction. The stress state of a complex shear occurs in a cylindrical body of infinite length under the action of loads directed along the generators of the cylinder and constant along the generators [1]. At the same time, with a sufficiently large load, both elastic and plastic zones appear in the body. As in any problem of this kind, it is necessary to find a previously unknown boundary separating the elastic and plastic zones. Finding such a boundary is not an easy task, but the specificity of elasticplastic problems about complex shear is that the solution of such problems is easier than the solution of similar elastic problems. Apparently, this fact was first noted by G. P. Cherepanov [1].

A lot of research is devoted to the elastic-plastic problems of complex shear in the case of homogeneous and isotropic plasticity, and its review can be seen, for example, in [1]. In all articles that solve complex shear problems, the representation of stresses and displacements in the elastic zone in a complex form is significantly used. In this research, we solve the problem of complex shear using conservation laws. For the first time, plasticity problems were solved using conservation laws in [2–6]. In articles [3; 7–12], the method of conservation laws was successfully applied to finding elastic-plastic rods and beams. In this article, this technique is used for the first time to solve elastic-plastic problems. And it is assumed that in the plastic area, the yield strength is a function of the coordinates of the point at which the stress state is studied. It is known that the elastic properties of structural materials can be homogeneous and isotropic, and their yield strength and strength – inhomogeneous. This situation is observed, for example, in the case of neutron bombardment of structural materials [13]. This article will study exactly this situation.

1. Basic ratios. The shear and stress fields in this case are as follows [1]

u = V = 0, w = w ( x , y ) ,

^CT x = ^CT y ^CT z = T xy = 0,                 (1)

tesian coordinates, the z axis is directed parallel to the generator дт1 дт2    . .                         .

— +--= 0, ( equilibrium equation); (2)

дx   дy дW     д8W t1 = G—, t2 = G—, (Hooke's law).      (3)

д x д y

Here G – a constant called the shear modulus.

From (2), (3) follow the ratios in the elastic zone

д w д w дx2 дy y " дт1 _ дт2 ay ~ "ax"

From (2) and (5) it follows that t ¹, t ² satisfy the

Cauchy-Riemann equations

^ =^1 1 ₊5T 2 = 0, F 2 = гт 1 д x   д y          д y

= 0. д y

In the plastic area, there is a ratio (2), and also

( t ¹)² + ( t ²)² = k ² (the yield condition); (7)

2 д w    i д w _ . .       . .

т — = т — (Genki equation). (8) д x     д y

Here k ( x , y ) – some smooth function equal to the yield strength at pure shear [13].

At the boundary of elastic and plastic areas, stresses and shears are assumed to be continuous.

2. Conservation laws. The conservation law for the

system of equations (6) is the following ratio

д A ( x , y , t ¹, t ² ) д B ( x , y , t ¹, t ² ) д x             д y

= to ¹ F +to ² F ₂,

^T xz = ^{t 1} ( x , У ) , ^T yz = ^T 2 ( x , У ) .

Here u, v , w - shear vector components, ct _x , ct _y ,

ct _z , t xy , t _xz , t _yz - stress tensor components, x , y , z - car-

where to i = to i ( x , y , t ¹, t ²) - some functions that are simultaneously not not equal to zero.

Comment. A more general definition of conservation laws and their use in the mechanics of a deformable solid can be found, for example, in [4; 6; 14]. In [15], you can

read about the application of the group analysis technique for constructing solutions for the equations of inhomogeneous elasticity theory.

For the purposes set out in the article, a simplified formulation in the form of (9) is quite appropriate.

In the case of (9), the values A and B are called the components of the conserved current.

Let us assume that components A And B have the following form

A = aV + рЧ ² +Y ¹ , B = a ² T + р ² т ² + y ² , (10) where a i = a i ( x , y ) , P i = P i ( x , y ) , у i = y i ( x , y ) - some smooth functions to be defined. Substituting (10) in (9), as a result we get

• ^a X ^T + ^a 1 ^T X ⁺ P X ^т 2 +P 1 ^T 2 + y X ^+a 2 ^{T + a} 2 ^T y + P 2 ^т 2 ⁺

• ⁺ p ² T 2 + y 2 =to 1 ( t X + T 2 ) + to ² ( l y, ^- т 2 ) = 0, ⁽¹¹⁾ where the index at the bottom means the derivative of the corresponding variable.

From (11) we get

Where S - area, 5 S - its piecewise smooth border. All functions included in (15) are assumed to be smooth.

Elastic plastic problem for an arbitrary hole in the case when the plastic area covers the entire hole. Let С – a piecewise smooth contour with a load applied to it l 1т1 + l2т2 =тn,|тn| < k,

where ( l ¹ , l ² ) – the components of the normal vector to contour C . The contour of the plastic area L completely covers the hole C (see fig. 1).

In this case, in addition to condition (16), the yield condition (7) on the contour C is also satisfied. Thus, there are two conditions on C :

1 1 т ¹ + l ² т ² =т _n , ( т ¹ ) ² + ( т ² ) ² = k ² .       (17)

From conditions (17), we find the stress tensor components on the conour C :

^T = ^T n ± l \^{k -T} n -.

2  2122

• ^т = t n l + 1 kk ^-т n .

  
  

  a ¹ =ro 1 , p ¹ =-ю ², a ² =ю ², p ² =№> * ,

  a X + a 2 = 0, P X +P 2 = 0, y X +У 2 = 0.

  From (12), excluding m i we get

  ^a X —P X = 0, P X ^+a y = 0, y X +У 2 = 0.

  Due to the ratios (12), the components of the served current have the form

  A = a 1 T 1 +Р 1 т 2 +У ¹ , B = -р ¹ т ¹ +a 1 T ² +y ² .

  
  
  
  
  
  

  con-

  
  
  
  

  Since the right part (9) is zero, by Green formula we obtain

  U S ( A_X ⁺ B y ) dXdy = i s S Ady — BdX =

  = J₉ S ( a 1 T 1 +Р 1 т ² +У ¹) dy - ( -P 1 T ¹ +a 1 T ² +y ² ) dX = 0.

  
  

  Further, for certainty in formulas (18), we will choose the upper sign.

  4. The use of conservation laws to find the stress tensor component in the area. Let the point M ( X m , y m ) lie outside of contour C . Let us build a radius £ circle

  
  

  centered at point M. We have £ :( x - X m ) ² + ( y - y m ) ² = £ ² . Let D be a straight line connecting point M with contour C . We get a closed contour consisting of a circle £ , a straight line D , and contour C (fig. 2).

  From (15) we get

  
  

  ^ Ady - Bdx + J Ady - Bdx +

  d ⁺

  + J Ady - Bdx + J Ady - Bdx = 0.

  
  
  
  

  D ^-

  

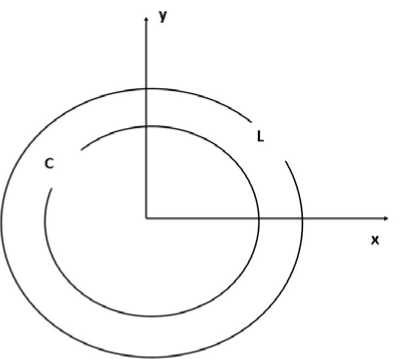
  Fig. 1. Elastic-plastic problem for an arbitrary hole in the case when the plastic area covers the entire hole

  
  

Рис. 1. Упруго пластическая задача для произвольного отверстия в случае, когда пластическая область охватывает все отверстие

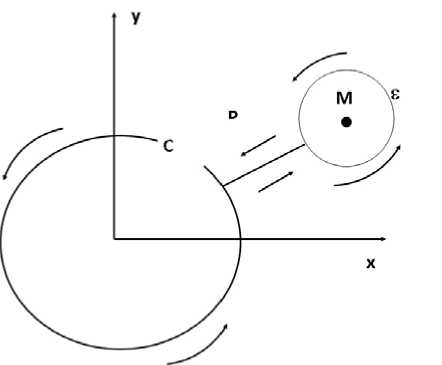
Fig. 2. Closed contour consisting of a circle £ , straight line D , and contour C

Рис. 2. Замкнутый контур, состоящий из окружности £ , прямой D и контура С

The sum of the second and third terms in (19) is zero, since the integrals are calculated in different directions. Finally from (19) we have

J CAdy - Bdx = -< J Ady - Bdx .        (20)

We transform the right side of equation (20) by introducing parameterization x = £ coscos t , y = £ sint , 0 <  t <  2 n . As a result, we have

Ady - Bdx = £ J 0 ( Acost + Bsint ) dt .

Let in (15)

a¹ = -x- , в¹ = x ² + y

Then from (21) we get

^^^^^^B

y

.

x + y

J A 1 dy - B 1 dx = £ J 0 ( A 1 cost + B 1 sint ) dt =

= J () ^{2 nT 1 dt} = ^{2 ПТ} 1 ( x m , У т ) .

The last equality in (23) is obtained using the theorem

on the mean at Let in (15)

a ¹

£ tending to zero.

„ y „ , R 1 =            .

x ² + y        x ² + y

Then from (21) we get

A ₂ dy - B ₂ dx = £ J 0 ( A ₂ cost + B ₂ sint ) dt = = Jo^ ^{2 dt} = ^{2 nT} 2 ( x m ’ y m ) .

The last equality in (25) is obtained using the theorem on the mean at £ tending to zero.

The last equality in (25) is obtained using the theorem on the mean at £ tending to zero.

From the formula (20), as well as from (23) and (25), we get

J C A dy - B i dx = — 2 ^nT1 ( x_m , У т ) , J C ^A 2 dy ^{- B} 2 dx = ^-2nT2 ( x m , У т ) ^.

Formulas (26) make it possible to find the components of the stress tensor at any point outside the contour C . This allows to set the boundary between the elastic and plastic areass. If the condition of plasticity ( t ¹)² + ( t ²)² = k ² is satisfied at a point x_m , y_m , then this point belongs to the plastic area, when the condition ( t ¹)² + ( t ²)² <  k ² is satisfied, to the elastic.

Comment. The above formulas allow us to solve elastic-plastic problems, even if the plastic contour does not completely cover the contour C, provided that the plasticity condition is satisfied on the contour C (7).