Elastic-plastic torsion of a two-layer rod

The article continues a series of papers devoted to the use of conservation laws for solving boundary-value problems of the equations of mechanics of a deformable solid body. The equations of elasticity and plasticity have been studied for long with the help of symmetries [1; 2]. Further, it was shown that conservation laws can be used and they were used to solve boundary-value problems for twodimensional plasticity equations [3–12]. These works have shown that conservation laws are more suitable for solving boundary-value problems than point symmetries, which were previously counted on [2]. This is explained by the fact that symmetries are local in nature, unlike conservation laws, they are global in nature. Further, conservation laws were applied to solve elastic-plastic problems of rod torsion and cantilever bending, as well as to solve elastic-plastic problems for finite-size plates weakened by holes [13–18]. In this paper, we show that conservation laws can also be used to solve boundary-value problems for multilayer materials.

Statement of problem

Let us consider a straight rod, the cross section of which is shown in Fig. 1. Let the areas S and S be occupied by elastic-plastic isotropic materials, in which the yield strength in pure shear is the same and it is equal to k ; the Lame elastic constants are different and equal to λ , µ and λ , µ respectively. Let the dividing line of materials be straight. We choose ох coordinate axis along the dividing line. As usual, it is assumed that the lateral face of the rod is stress-free, and the rod is twisted by a pair of forces with the moment

M = ∫∫ ( y σ ₁₃ - x σ ₂₃) dxdy .

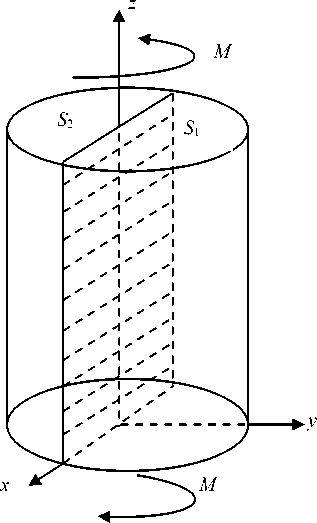
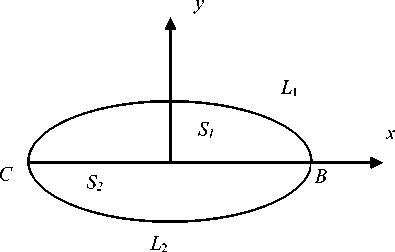
Рис. 1. Кручение двухслойного стержня

Fig. 1. Twisting of a two-layer rod

In this case the equations describing the stress state in the S i = 1,2 area have the following form

F ₁ = ∂ _x σ ₁₃ + ∂ _y σ ₂₃ = 0, F ₂ = ∂ _y σ ₁₃ -∂ _x σ ₂₃ +µ _i ω= 0,   µ _i ω= K_i ,              (1)

where σ , σ – stress components, ω – twist angle (it is assumed to be constant).

On the lateral face of the rod the following conditions are satisfied

σ13n1 + σ23n2 = 0, σ + σ = k , which mean that the lateral face is free from stress and is in a plastic state.

From (2) we obtain

σ ₁₃ = kn ₁ , σ ₂₃ = - kn ₂ .

We also assume that the components of the stress tensor are continuous at the CD boundary, which means that there is no stress discontinuity for this rod along the CD boundary.

Conservation laws

We are searching for the conservation law in the following form

A x + B y =ρ 1 F 1 +ρ 2 F 2 ,                                 (4)

where ρ , ρ are some functions that are simultaneously not identically equal to zero; the lower indexes mean derivatives with respect to the corresponding variables.

Comment. More detailed information about conservation laws, their calculation and use can be found in the literature cited above.

Let

A = α1u + α2v+α3, B = β1u + β2v+ β3,(5)

where for convinience we assumed σ = u,σ  = v, α1,α2,α3, β1,β2,β3 to be the functions only of x,y.

Substituting (5) into (4) we obtain 122112   12   3 3  2

α = β , α = -β , αx- α y= 0, α y+ αx= 0, αx + β y = -α

Let

α1(i)-α2(i)=0, α1(i)+α2(i)=0, α3(i0+β3(i0=-α2K, i=1,2

xy  yx  xyi

The index i in parentheses corresponds to the S_i area.

Let us suppose that at the x ₀ , y ₀ point the subintegral functions have a singularity and this point is in a circle of the radius ε :( x - x ₀)² + ( y - y ₀)² = ε ² (Fig. 2), then from (4) we obtain

∫∫ ( A_x + B_y ) dxdy = ∫∫ ( A ¹ _x + B ¹ _y ) dxdy + ∫∫ ( A ² _x + B ² _y ) dxdy = - ∫ A ¹ dy - B ¹ dx +

S                           ^S 1                          ^S 2                             ε

+

∫ A ¹ dy - B ¹ dx + ∫ A ² dy - B ² dx + ∫ A ¹ dy - B ¹ dx + ∫ A ² dy - B ² dx = 0

L ₁                    L ₂

CD            DC

We have along CD

∫ A ¹ dy - B ¹ dx + ∫ A ² dy - B ² dx = ∫ ( α ¹⁽¹⁾ u + α ²⁽¹⁾ v + α ³⁽¹⁾) dy - ( -α ²⁽¹⁾ u + α ¹⁽¹⁾ v + β ³⁽¹⁾) dx + CD            DC             CD

+ ∫ ( α ¹⁽²⁾ u + α ²⁽²⁾ v + α ³⁽²⁾) dy - ( -α ²⁽²⁾ u + α ¹⁽²⁾ v + β ³⁽²⁾) dx = 0

DC

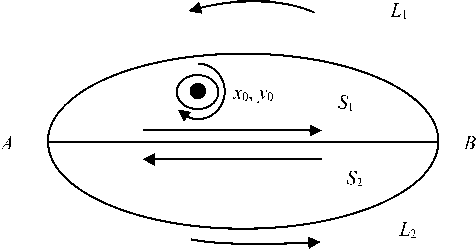
Рис. 2. Схема взятия интегралов по поперечному сечению

Fig. 2. The scheme of taking integrals over the cross section

Since along the CD dy = 0, we assume that P 3( i ) = 0, a 3( i ) = a ² ( i ) K , therefore a ¹⁽¹ ) = a ¹⁽²⁾, a ²⁽¹ ) =a ²⁽²⁾.

As a result we obtain j A1 dy - B1 dx = j A1 dy - B dx + J A2 dy - B2 dx.

£                     L1

We use the formula (8) to find the functions u , v at the point

In order to do that, let us consider the solution to the equations (7) in the following form

1         x - xn           2           y — У о           3           x - Хл a =-------5---0------y, a =------0------a = wg1arctg----0.(9)

^{( x - x} o ) + ⁽ y ^- y 0 )          ^{( x - x} 0 ) + ⁽ y ^- y 0 )                  y ^- y 0

Substituting (9) into (8) we obtain j A1 dy - B1 dx = j (a1u + a2v + a3)dy - (-a2u + a1 v)dx = ££ x  xо

. ( x - x о ) ² + ( y - y о ) ²

u

-

y ^- y 0

^{( x - x} 0 )^{2 + ( y - y} 0 )²

x-x v Iw^arctg----0- y - У о J

dy

-

y - y

[ ( x - x о ) ² + ( y - y о ) ²

Л u dx +

J

+ j

£

Let x - x ₀ =£ cos ф , y - y ₀ =£ sin ф .

Then we obtain

2 n

x - x ₀

^{( x - x} 0 )² + ^{( y - y} 0 )²

v dx

2 n

j A¹ dy - B¹ dx = j [( u cos p + v sin ^ )cos p + ( u sin (p + v cos ^ )sin p ] d p = j ud p = 2 n u ( x ₀, y ₀).

£

The last equality uses the mean value theorem and the passage to the limit £ ^ 0.

As a result, from the formula (8) it follows

^{2 n}^ 13^{( x} о , У o ) =

j

L 1 <

x - x ₀

y ^- y 0

^{( x - x} o ) + ^{( y - y} o )       ^{( x - x} 0 ) + ^{( y - y} 0 )

,              x = xn kn 2 +w^1arctg----0

У ^- У o

dy -

—

---4^--- I kn

^{( x — x} o ) ^{+ ( У — У} o )

—

x — x0         ,,

------- ---o------- kn 2

(x — x o) + (У — У o)

⁺ f

L 2 <

x — x _o

y ^— y 0

^{( x — x} o ) + ^{( У — У} o )       ^{( x — x} o ) + ^{( У — У} o )

,               x = xn kn 2 + wg2arctg----0

У ^— У o

dy —

---^У^---У kn —

^{( x — x} o ) ^{+ ( У — У} o )

x — x ₀

( ^{x — x} o ) 2 + ( У ^{— y} o ⁾²

kn 2

J

dx .

Let us consider the solution to the equations (7) in the form a1 =------У—^o------, a2

^{( x — x} o) ^{+ ( У — У} o)

x — x ₀

^{( x — x} o^{)2 + ( У — У} o⁾²

^a 3 = ¹ ®H 2 ln(( ^{x — x} 0 ) 2 + ( У ^— У o⁾²⁾ .

Substituting (11) into (8) we obtain

^{2 п}^ 2з ( ^x o , У o ) =

f (—F ^--kn i

L ^{( x — x} o ) ^{+ (} У ^— У o )

—

------T x—x ^o------Г ^kn 2 ^{+ 1} ®^ 2 ^ln(( x ^— x o ^{)2 + (} У ^— У o ⁾² ) d ^—

( x — x o )² + ( У — У o )^{2      2}

— (-- x—x -----У kn ₁ +------ ^У— ^{У o}----- - kn ₂) dx +

⁽ x ^— x o ) + ⁽ У ^— У o )       ⁽ x ^— x o ) + ⁽ У ^— У o )                            (12)

+ f (-- У — ^o----- kn i +

L ^{( x — x} o ) ^{+ (} У ^— У o )

x — x _o

^{( x — x} o ⁾² + ^{( У — У} o ⁾²

kn 2 ^{+ 1} ®^ 2 ^ln(( x ^— x o ^{)2 + (} У ^— У o ⁾² )& ^—

— (-- x—x -----y kn ₁ +------ ^У— ^{У o}----- - kn ₂) dx .

⁽ x ^— x o ) + ⁽ У ^— У o )       ⁽ x ^— x o ) + ⁽ У ^— У o )

Conclusion

The formulae (10), (12) allow us to calculate the values of the stress tensor components at all points of the cross section. Further in each point of   x0, y0   the plasticity condition is checked. The points where                belong to the elastic zone, and all the other points – to the plastic one. Thus, the described procedure makes it possible to identify plastic and elastic zones and construct an elastic-plastic boundary, which was unknown in advance and had to be determined.