Electrically controlled optical spectral filters for DWDM communication networks based on multiplexed three-layer holographic PPM-LC diffraction structures

The use of diffraction optics is of great relevance in modern science and technology. This field of optics makes it possible to create and study optical elements based on diffraction phenomena, which has a wide range of applications. Diffractive elements are used in optical communications systems, 3D-displays, virtual, augmented and mixed reality, as well as in other fields such as robotics and medicine. The task of developing the characteristics of diffraction optics to improve the performance of dense wavelength division multiplexing (DWDM) optical systems, increase the speed of information transfer and innovation in modern technologies is urgent.

As the field of optical communication systems advances rapidly, researchers are tasked with the challenge of identifying not only novel but also costeffective and efficient components for these systems from a manufacturing standpoint. Diffractive optical elements (DOEs), which utilize multilayer inhomogeneous holographic diffraction structures (MIHDS), could be widely implemented in optical communication networks. They hold potential for use as optical spectral filters among other applications, as indicated in references [1–10], in hyperspectral optical systems [11, 12], as well as encoding information [13, 14].

For spectral filtering of optical radiation, it is proposed to use a structure consisting of a set of thin films with photopolymer material and nematic liquid crystals (PPM-LC), separated by buffer layers that are not a photosensitive medium, in which diffraction gratings will be recorded using the holographic method. When such structures are read by optical radiation, interference of light rays occurs between the layers, which contributes to a special type of angular selectivity. This type of angular selectivity is a set of local maxima and minima, the number and width of which depend on various parameters, including the number of diffraction layers and the ratio of their thicknesses [1, 5, 8, 17, 18]. By interpreting local maxima as passbands for specific wavelengths when deviating from Bragg diffraction conditions, such structures can be used for spectral filtering of optical radiation. The technique of forming diffraction structures in photopolymer materials has also been previously studied in [15–16].

At the same time, the task of finding ways to increase the capacity of the MIHDS in order to increase the number of spectral channels remains urgent. One of the possible ways to achieve this task is to record multiplexed MIHDS, which have broadening of the angular and spectral characteristics due to the recording of several diffraction structures.

Thus, the purpose of this work is to study the diffraction characteristics of multiplexed MIHDS formed in PPM-LC.

Diffraction of light by MIHDS with PPM-LC

To describe the process of light diffraction by multiplexed MIHDS in PPM-LC, we will use the developed theoretical model, which was presented earlier in [1]. When considering Bragg diffraction of light beams on multiplexed MIHDS, the amplitudes of interacting waves will be determined by systems of coupled wave equations (CWE) in partial derivatives. For the case of a high LC concentration, at which the diffraction layer has a smooth optical inhomogeneity in thickness, when solving the CWE system, the parameter of the integral phase mismatch is approximated due to its complex dependence [1]. The diagram of light diffraction by multiplexed MIHDS in PPM-LC is shown in Fig. 1 in aperture coordinates.

In the case of Bragg diffraction of light in optically inhomogeneous PPM-LC layers, one can use the method of slowly varying amplitudes and determine the amplitudes of interacting waves using a system of partial differential equations of coupled waves of the following form [19]:

N m₀ n , n h -V E m , n , n h =

= - iC m , n , n h - n m , n , n h - E m , n , n h - exp [+ i &

N m,n , n_{h -} V E l?¹ , n , n h =

= - iC m , ⁿ , n h - n m , ⁿ , n h - E m , ⁿ , n h - exp [- i &

the spatial distributions and angular spectra of diffracting beams [1]:

Ж

E m ¹ (0) = J E m (l )exp [ ik m l 9 ] dl ,

-Ю

where

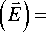
where 0 is the angle that determines the orientation of plane-wave components in relation to wave normals, and l = ^ 0 , ^ i .

ro ( < m , ⁿ , n h A e ⁿ , n h ( r) e mn ■ n^h ) ( с с n m ⁿ , n^h cos e m o n ’ n h ) ^{- 1}

are coupling coefficients, j ={0,1} - diffraction order, r – radius vector, E 1 ^{m , n , nh} – diffracted radiation field E 0 ^{m , n , nh} – transmitted radiation field, n h – number of the recorded hologram, n =1... N - number of diffraction layers, N -last layer number, N_r ^m ₀ ^, _,1 ^{n , nh} – group normals E ₀ ^m _,1 ^{, n , nh} ,the direction of which differs from the wave normals N ₀ ^m _,1 ^{, n , nh} by the angle of drift , ω – radiation frequency, A e ⁿ ■ n h - change in dielectric constant , cos e m^ ’ n h ( N mn ’ n h - N m0 Г ) , m = o , e - index, corresponding to ordinary and extraordinary waves, n ₁ ^{m , n , nh} determines the normalized refractive index profile of the first harmonic of the HDS, &^m ■ ⁿ ■ n h ( r, E ) is the integral phase mismatch parameter, which is expressed as:

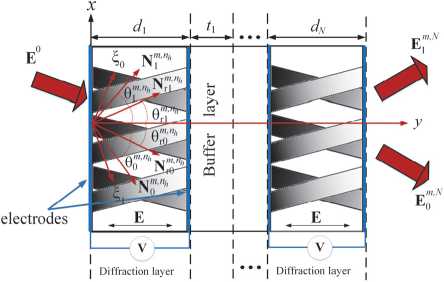
Fig. 1. Scheme of light diffraction by multiplexed MIHDS in PPM-LC

d n

& m , n , n h ( E ) = J A K

( y , E ) dy,

a k ^m • ⁿ • n h = |a K ^m • ⁿ • n h |- y ₀ ,

—►

where A K ^m ■ ⁿ ■ n^h - phase mismatch vector.

In the case of near-field diffraction (Fig. 1), the expressions of the light fields for the zero and first diffraction order at the output of the multiplexed MIHDS can be defined as:

d n

E nn (n) = e o ■ n ■ n h E o ■ n ■ n h (n) exp[ - i J k o ■ n ■ n h dr] +

d n

+ e e ■ "’" h E e ■ ⁿ ■ n h (n)exp[ - i J k e ■ ⁿ ■ n h dr],

d n

E _o ⁿ ■ n h © = e 0 ■ ⁿ ■ n h E 0 ■ ⁿ ■ n h ©exp[ - i J k o ■ ⁿ ■ n h dr] +

d n

+ e e ■ n ■ n^h E 0 ■ n ■ n h ©exp[ - i J k e ■ n ■ n h dr] .

The coordinate transformation equations have the form:

Fig. 2. Scheme of wave propagation in MIHDS in PPM-LC

To describe the transformation of plane light waves in multilayer media, a matrix method is used with the transition from the amplitude distributions of the Fourier frequency components of diffracting beams to their angular spectra. Thus, as a result of the process of converting the frequency-angular spectra of interacting light beams, the light field at the output of a multiplexed MIHDS can be represented as follows [1]:

E m , N = ( T m , N ,1 +   T m , N , n_h । T m , N , N h ) _- e 0

where

m , N , n h = T m , N , n h _- a m , N - 1, n h _-

_- A m ,1, n_{h -} T m ,1, n h

matrix transfer function of the entire MIHDS for n h rec-

orded hologram,

E ^m ■ N =

E mN ( E , 0 )

E m^N ( E , 0 )

^ o =-П о y + V o z , ^ i =-П 1 У + V i z ,

T 0 ^m 0^{, n , nh} ( E ,θ) T 10 ^{m , n , nh} ( E ,θ)

T 0 ^m 1^{, n , nh} ( E ,θ) T 11 ^{m , n , nh} ( E ,θ)

where v j = N j - y ₀, nj' = N_r j - z ₀. ^₀, ^ 1 - aperture coordinates.

To find the distribution of the diffraction field in the far zone, it is necessary to use the relationship between matrix transfer function,

E ⁰ ( E , θ) 0

A m , n , n h

buffer layer matrix function, N – number of diffraction layers, N h – number of recorded holograms. All other elements of the mathematical model are presented in detail in [1].

Numerical calculation

When performing a numerical calculation, the diffraction efficiency (DE) at the output of the multiplexed MIHDS will be determined by the expression:

nm,n (E, AK ) =

= [ n m , n ,1 ( E, A K ) + ... + n m , n , N h ( E, A K ) ] / N_h .

In numerical modeling, we will assume that the polarization of the incident radiation coincides with the polarization of its own extraordinary waves for each diffraction layer. Also, in the numerical calculation, a three-layer holographic diffraction structure (HDS) with uniform refractive index profiles recorded at the wavelength X 0 =1550 nm and angles between beams inside the sample in 2 0 =16 degrees. Simulation parameters: X _read=1550 nm - reading wavelength; d n = 20 ^m; t n =297 µm; N h =2 – number of recorded holograms; T ={-9,9} degrees - sample rotation angles during multiplexed recording. The above parameters were selected in such a way that the local maxima corresponded to the DWDM grid with a channel spacing of 0.8 nm, and specially selected sample rotation angles T made it possible to combine the angular selectivity of two arrays into one circuit at a level of local maxima not lower than –3 dB.

Fig. 3 shows the angular selectivity of a three-layer HDS under the influence of an external electric field with different polarities on all diffraction layers. The dependence is expressed in dB relative to the radiation intensity.

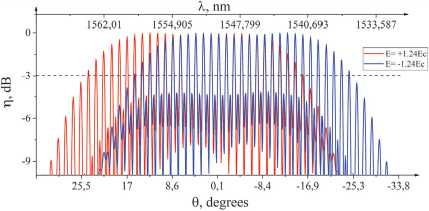
Fig. 3. Angular selectivity of a three-layer HDS under control of an external electric field

Thus, with multiplexed recording of MIHDS, it was possible to increase the number of spectral channels at the –3 dB level by almost 2 times, from 15 to 29. Under external electrical influence, which can have different polarities, it becomes possible to dynamically change the channel, namely, shift the channels to the right or to the left. Also, the use of a three-layer HDS made it possible to achieve narrower spectral bandwidths of 0.25 nm at a level of up to –3 dB, in contrast to two-layer structures with a bandwidth of 0.45 nm [1].

Fig. 4 shows the dependence of the diffraction efficiency of a multiplexed three-layer HDS with a smooth change in the linear polarization angle of the readout radiation from 0 to 90 degrees at a constant voltage of the applied electric field E=1.56Ec.

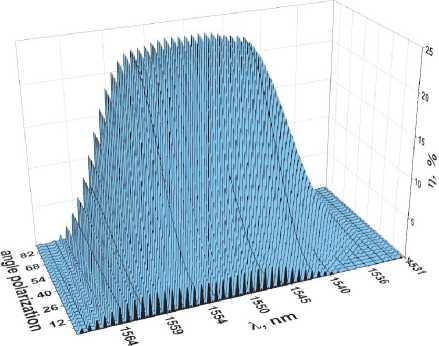
Fig. 4. Dependence of the diffraction efficiency of a multiplexed three-layer HDS with a smooth change in the polarization angle

When the polarization angle of the reading radiation is varied and when an external electric field is applied to all diffraction layers, light diffraction occurs, both at ordinary and extraordinary waves. When the polarization angle changes, the DE increases due to the diffraction of light on ordinary waves, while the angular selectivity at these waves does not depend on the voltage of the applied electric field. So, at a polarization angle of 0 degrees, the diffraction efficiency is 2.5 %, and at a polarization angle of 90 degrees, the diffraction efficiency increases by 9.6 times and amounts to 24 %. The channel displacement due to diffraction by extraordinary waves under applied voltage conditions is also shown.

Fig. 5 shows the angular selectivity of a three-layer HDS normalized relative to the maximum value for a discrete change in the linear polarization angle of the readout radiation 0, 30 and 90 degrees at a constant voltage of the applied electric field E=1.56Ec.

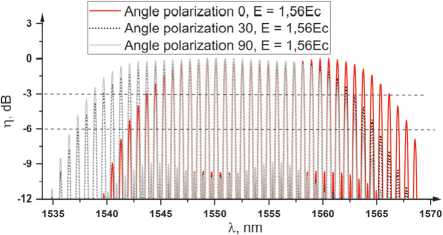
Fig. 5. Angular selectivity of a multiplexed three-layer HDS with a discrete change in the polarization angle

Thus, with a polarization angle of 90 degrees of the reading radiation, light diffraction occurs only on ordinary waves; when the angle of a linearly polarized wave decreases, diffraction on extraordinary waves appears, as a result of which the DE changes and an increase in the number of channels is demonstrated when normalized relative to the maximum value. With a polarization angle of 30 degrees of the reading radiation, the number of channels increases by 5 at a level of -6 dB; with a polarization of 0 degrees, the number of channels increases by 6 at a constant voltage of the applied electric field. As a result, when the angle of the linearly polarized wave of the readout radiation changes, the number of channels increases from 29 to 35 at a constant field strength.

Thus, with a maximum diffraction efficiency for a multiplexed three-layer GDS of 23 %, and also taking into account the insertion attenuation of the material (0.4 dB) and the level of lateral local maxima up to – 3 dB, the total insertion attenuation in the group optical radiation in the worst case will be up to 9.4 dB. Therefore, with 35 spectral channels, the maximum attenuation will be 25.3 dB.

Conclusion

This paper presents the diffraction characteristics of electrically controlled multiplexed three-layer holographic PPM-LC diffraction structures, demonstrating the possibility of broadening the angular and spectral characteristics compared to conventional multilayer structures by recording multiple diffraction gratings. In addition, the possibility of their use in optical DWDM communication networks with the possibility of channel tuning is shown.

When an external electric field is applied to all diffraction layers, as well as by changing the polarization angle of the reading light wave, it is possible to increase the number of channels due to the diffraction of light both on ordinary waves, independent of voltage, and on extraordinary waves, for which the angular selectivity is shifted.

Acknowledgements

The work was carried out within the framework of the Priority 2030 strategic academic leadership program.