Empirical Analysis of HPC Using Different Programming Models

Published Online June 2016 in MECS

High performance parallel computing concept has been around since last decade [4]. According to Moore’s law, a rapid development is still outgrowth in system architecture and hardware to develop the high performance parallel machines while the growth in parallel software development is comparatively low. The one of the major reason of huge gap between parallel hardware and software might be the lack of availability of desirable parallel programming models [4] and this is the reason, traditional processing models are not approachable to the computational applications where a massive level parallelism is required. The concept of HPC is becoming more requiring day by day almost in every field and this demand is directly proportional to parallelizing coding schemes.

During last decade, many multithreading programming models has been introduced such as Message passing interface (MPI) the most commonly usage for parallelizing cluster based application, Compute Unified Device Architecture (CUDA) to parallelism graphical processing unit (GPU) and another one shared memory model as Open Multi-Processing (OpenMP). These programming models facilitate to system by providing massive level parallelism in data and communication between multiple platforms. Another advantage to utilizing these models is the provision of distributed shared-memory models. Moreover, these parallel programming models are supportive for data driven with dynamic behavior by following data driven multithreading (DDM) principle. Keeping in view the principle of DDM, we have implemented these models for performance evaluation in multiple applications including massive amount of computation requiring operations are matrix multiplication. This high computational operation is evaluated using HPC system having GPU technology as well. In few years, NVIDIA introduced a general purpose programming model as CUDA which is used to write massive level parallel application by providing multithreaded blocks and shared memory [5]. This model is programmed specifically for multithreaded core GPUs to make it possible for HPC parallelism for both general purpose and graphic processing applications.

In this paper, we have implemented the computational operations by using data driven multithreaded programming models that has been discussed in other sections. Rest of the paper is documented as follows, in section II we have discussed the programming languages used in this paper, section III provides the related work where we have discussed the different approaches used for HPC provision. Section IV elaborates the experiments on operations using programming models, further section V consists of finding and results where we have compared the DDM programming models with traditional computing approaches.

• II.    Programming Models

In this section we have discussed the programming models/ languages that have been used in this paper for performance evaluation. We have discussed CUDA, OpenMP and MPI each one in detail with respect to HPC parallelism in a system.

• A.    CUDA

Leading to programming model, in order to achieve a massive level parallelism, many computer companies are dramatically increasing on-chip parallelism. Moreover, in field of HPC parallelism, GPU is the maximum exponent hardware because of its low cost and massive parallel processing power. General-Purpose Graphics Processing Units is apparent promising building blocks for HPC. CUDA is one of a parallel computing model that could provide massive amount of parallelism in applications to gain the high performance and throughput [6]. CUDA is a programming paradigm to compute NVIDA GPU, which is supportive for different programming languages such as C++, FORTRAN [5].

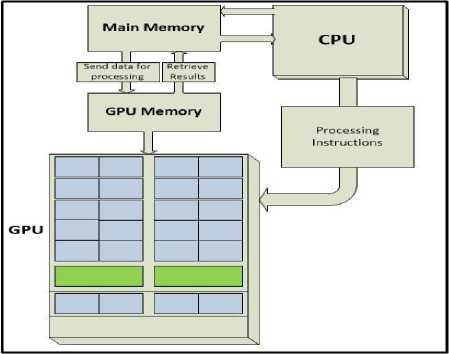
Fig.1. GPU Process flow.

The traditional processing system using CPU has multiple cores is still serial processing and implementation of this processing technique is very costly in various applications. Many real life applications are requiring high performance computation that enforces us to digging in parallelization concept in order to achieve the expected results. In recent years, NVIDIA emphasized for this challenge and introduced the parallel processing unit such as a graphical processing unit (GPU) that consist of millions of cores on a single chip. It has improved the programming ability for single instruction, multi data (SIMD) as well. The most interesting thing is GPU combining with the CPU are available nowadays to induce for both graphical processing and general purpose processing called GPGPU. The fact from the experience is that the use of GPGPU has enhanced the power of computation and mathematical calculations very efficiently. More specifically, the purpose of GPU design is to make faster execution of arithmetic and algebraic expressions by parallelizing the code. A basic flow of GPU working within a standalone machine is as follows in figure 1.

• B.    OpenMP

In contrast, the OpenMP such a great programming model that that supports shared memory multi-processing programming platform which is supportive in many programming languages such as FORTRAN, Visual C++ and C. The basic idea behind OpenMP is data-shared parallel execution. Number of loops could be parallelized easily just by adding OpenMP directives. The code inserted in these directives executes in parallel on multicores in the form of basic OpenMP unit called “Thread” [12]. As the basic objective of OpenMP is to achieve HPC by parallelizing programming code but during coding there are still some fallacies and unexpected observations from the experiments which enforce to digging in OpenMP deeply and provide the methods to stay away from these obstacles toward HPC parallelism [13].

• C.    MPI

In distributed memory system, almost this is unachievable to make possible the communication through sharing number of variables. ARMCI annoyed as Aggregate Remote Copy Interface is one of the model that make it possible to allow a programming model between shared memory and message passing [15]. A standardize form of this model was introduced as Message Passing Interface (MPI). MPI is very famous and cluster based programming model specifically for message passing between multi-core systems. MPI offers significant set of libraries that are used to parallelize the application letting in collective and message passing operations. The advantage to use MPI is standardization in syntax that is implementable on any architecture. MPI library is necessary to be linked whenever a program followed by MPI is going to be compiled using ordinary compilers. On distributed computing system architectures, MPI is currently the de facto standard for HPC applications [22].

• III.    Related Work

In this section we have discussed the some parallel programming models and techniques that have been adopted to enhance HPC parallelism provision by using multicores. Some of these models are useful and applicable toward HPC parallelism if the weak areas could be addressed pointed by the authors.

• A.    DDM applications

C. Christofi, G. Michael and P. Evripidou, discussed HPC parallelism where they evaluated preliminary data driven multithreading. In their experiments, they used DDM directives to get efficient results for large level applications. Further they computed three massive level operations to evaluate the performance between DDM approaches and PLASMA. PLASMA was developed to solve Linear Algebraic Package problems (LAPAK). They implemented DDM approach for different complex problem computation such as large number of matrix multiplication, LU decomposition which is very complex arithmetic operation and Cholesky decomposition operation. At 48 cores system configuration, they concluded from the experiments that the DDM approach generated much better results than the PLASMA with respect to performance and scalability. But on increasing the number of cores the performance is low in DDM in LU and Cholesky operations [8].

• B.    PLASMA

Another one most famous parallel computing model is PLASMA library for multicore processors implemented in many linear algebraic computing applications using C and FORTRAN programming languages. It is applicable for dense systems where a high computation power is required such as matrix calculation and factorization, linear equations etc. In order to accomplish the high performance using multicore architectures, PLASMA trusts only on such kind of algorithms which provide fine results with granularity parallelism [9]. In an empirical study, some experiments were carried on different multicore architectures to compare PLASMA with two another linear algebraic packages such as ScaLAPACK and LAPACK and concluded that PLASMA is one linear algebraic package which provides data distribution facility on cores. The interesting thing for PLASMA is that it support the dynamic scheduling between different tasks by imposing data dependency [8]. On other hand, PLASMA doesn’t support to eigenvalue problems and band matrices as the same behavior was found in LAPACK [9].

• C.    TFluxSCC

TFluxSCC is another DDM based approach to run on multicore processor for large level computation applications. TFluxSCC is an acronym for TFlux singlechip Cloud Computing that is basically an extension of DDM developed to exploit the multicore processors parallelism. Therefore, in order to reduce the resource consumption, a non-centralized runtime system was as TFluxSCC was proposed where TSU (having control of execution unit) functionalities were distributed on each core. One major advantage of TFluxSCC is the scalability in high performance computing parallelism for multicore processors without demanding cache-coherency support. The proposed approach was implemented on 48-core Intel Single-chip which is very small amount of cores as compare to HPC parallelism requirement. So, using this approach, a lot of work is required to meet HPC parallelism [10].

• D.    SMPS

Symmetric Multiprocessors superscalar is a programing model that emphasized on multicore processing. SMPS is DDM based parallel computing model that employ the pragmas which has ability to detection of atomic parts of code and which are capsulized in several functions. Further these pragmas information is utilized by SMPS compiler to parallelize the application [11]. SMPS is just like Cilk scheduling algorithm that also supportive multithreaded programming but MSPS has some extra features including tasks call handling living within the tasks just like simple function calls whereas Cilk doesn’t support the recursive feature [11].

• IV.    Mathematical Operation

In this section, we have discussed a very common but massive level computational mathematical operation such as Matrix multiplication that have been implemented in next experiment section using different programming models such as CUDA, OpenMP, MPI and Simple C-language to calculate the performance. Let’s have a basic overview of this operation before moving toward the experimental stage.

• A. Matric Multiplication

Matrix multiplication is another mathematical operation that is being used very commonly almost in all science fields. With the passage of time, it’s becoming more complex and requiring high computation to get the appropriate results. To make possible, many algorithms and mathematical formulas have been proposed whereas computer technology contribute in different way to overcome this challenge. One of the appropriate solution is parallel computation that has made the ease in all computational operations. In order to provide the parallel computation for matrix multiplication operations, many programming models have been proposed. We have discussed three models such as CUDA, OpenMP and MPI to compute matrix operations and evaluated the performance by empirical analysis in these models. A general formula [17] for matrix multiplication is given as follows:

C ik = Σ j A ij B jk               (1)

c11 c12 - - - c1 p c21 c22 - - - c2 p cn1 cn2 - - - cn p

a11 a12 - - - a1 m a12 a22 - - - a2 m an1 an2 - - - an m b11 b12 b21 c22

b m1 b m2

- - - b 1 p - - - b 2 p

- - - b mp

Fig.2. Matrix multiplication A * B

• V.    System Specification

This section consist of experiments of in different programming models to compute two common mathematical operation as massive amount of matrix multiplication, as it requires a high level computation hardware. Therefore we computed this operation on HPC server machine and evaluated the performance results in variation of matrix values. Let’s have a short overview of the machine specification that we used for the experiments.

• A.    Hardware Specification

  The NVIDIA Tesla k-40 a powerful GPU device which has a better performance capable to deliver not only for graphical processing but for general purpose processing as well [18]. As Tesla k-40 GPU is the one best professional computing device that have ability of accuracy in results using built in features such as ECC Memory and double precision. In order to achieve better results for our experiments, we installed Tesla k-40 GPU on FUJITSU Primergy RX 350 S7 HPC machine having Intel Xeon E5-2667 0 @ 2.90 GHz CPU inside it which consists 12 Physical Cores and 24 Logical Cores in it. The main memory size was 16 GB and 2.25 TB HDD.

• B.    Software Specification

  Regarding software specifications for our empirical analysis in different programming models, we used Windows 8.1 operation system on machine. We used Microsoft Visual Studio community 2013 as a development tool as which is integrated with new programming languages, features and development tools into this IDE [19]. While building application in visual studio, there are two modes such as “Release mode” and “Debug mode” . It depends nature of research and the language which is being used, but both has different configurations. Even we evaluated, the execution time is also vary on mode selection but in our case, we selected debug mode to build the project and made the experiments as presented in following section. We also have elaborated the necessary information for all the programming models used in this paper for experiments such as which system architecture has been implemented as shown in table 1.

• Table 1.    Programming models specification

• VI. experiments

In different experiments, we computed matrix multiplication operations using simple visual studio C++, OpenMP, MPI and CUDA programming model with variation in matrix size as shown in table 2. In order CPU processing time calculation we could use the general formula as follow:

CPU t = Seconds / program          ( 2)

As

[Seconds / program = (Instructions / program) *(Cycle / Instructions) * (Second / Cycle)]

Where

CPI = CPU Clock Cycles / Instruction count CPU clock cycles = ^CPIt ^x Ci)

Hence, T = I * CPI *   C [21]

In our  experiments,  we computed the  matrix multiplication operation with size variation on different programming models as shown in below table 1. For example in CUDA for private thread it has its own memory but for threads in block use shared memory. Similarly, for OpenMP is shared memory and for MPI is both distributed and shared. The logic of code written for matrix multiplication was almost same in all models but vary in implementation method in case of CUDA where we have to write some extra line of code (LOC) such as:

// to load matrix data from device memory to shared memory

As[ty][tx] = A[a + wA * ty + tx];

Bs[ty][tx] = B[b + wB * ty + tx];

// execute Synchronize to make sure the matrix data is loaded

__syncthreads ();

The time unit for evaluation was in “Sec” for all models as shown in Y-axis in graph figures.

• Table 2.    Experiment data

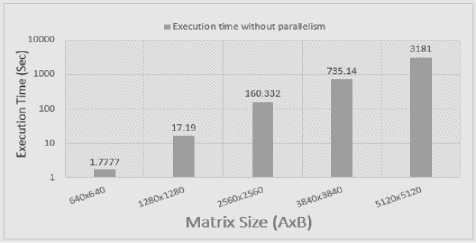
Fig.3. Matrix Multiplication without parallelism

In small amount of matrix multiplication by 640x640 and 1280x1280 matrix size, the results show clearly there is a small different in time execution which is negligible in C++, OpenMP and MPI. But if we notice this occurs only when we are not using the extra resource for parallel computing as GPU. The reason behind extra execution time in CUDA is the overhead of communication of between CPU and GPU when we Load the data from device memory to shared memory for each thread. We can conclude that at smaller level of processing, GPU utilization is not feasible by all aspects as time, coding and cost as well. Even if we notice the other evaluation time for 2560x2560 matrix size, Fig. 3,4,5 reveals the execution time is less than other methods in OpenMP with difference of 10 and 30 Sec C++, MPI respectively but we can see the big difference in CUDA time execution which is approximately more than 30%.

Below is the code sample parallelized using OpenMP.

#pragma omp parallel for default(none) shared(a,b,c) for (int i = 0; i < size; ++i) { for (int j = 0; j < size; ++j) { for (int k = 0; k < size; ++k) { c[i][j] += a[i][k] * b[k][j];

//printf(" %f ", c[i][j]);

}

}

}

Code Sample 1: OpenMP

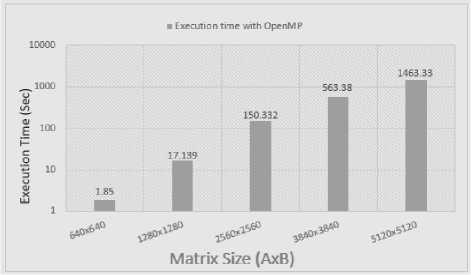
Fig.4. Matrix Multiplication using OpenMP

In 4th experiment with 3840 x 3840 matrix multiplication operation, the execution time is increasing with prominent variation. One interesting point for OpenMP, throughout evaluation, OpenMP taking less time as compared to others except in first experiment (but there was not a big difference). One thing more, in this operation there was a slightly difference of 20 Seconds in execution time in CUDA and Visual C++.

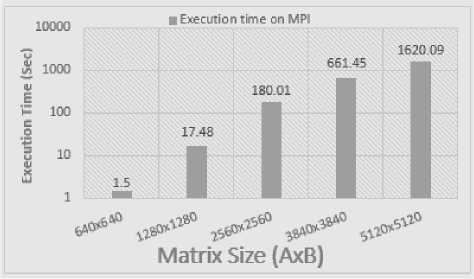
Fig.5. Matrix Multiplication using MPI

In our last experiment with very large number 5120x5120 matrix size , the output is totally different in all models. The parallelize code is showing the actual performance of parallel approach in this massive level operation. As we can see the code written in simple Visual studio, it takes almost 53 minutes which is very large time as compared to parallel computing models execution time as shown in fig 9. In contrast, OpenMP is showing still fast computation as compared to CUDA and MPI. CUDA is still take more time than MPI and OpenMP.

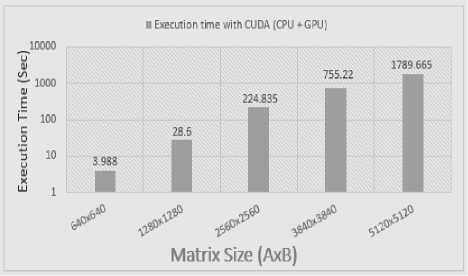
Fig.6. Matrix Multiplication using CUDA both (GPU+CPU)

To understand why CUDA is taking extra time even using GPU, we evaluated the actual processing time on GPU as shown in fig 8. The operation processing on GPU device excluding the CPU interaction with GPU is very small time in Mili-Seconds . As shown in fig 7, for processing of 5120x5120 matrix size , GPU takes less than 6 Sec . On other hand, the complete processing takes 1789.75 Secs which shows very large difference in CPU and GPU computation.

Intuitively the machine (or CPU) is said to be faster or has better performance running this program if the total execution time is shorter [21]. We can use the formula given in (3) to calculate speed up when using CPU along GPU multicores.

Speed up = (CPUt – GPUt ) / CPUt * 100% [20] (3)

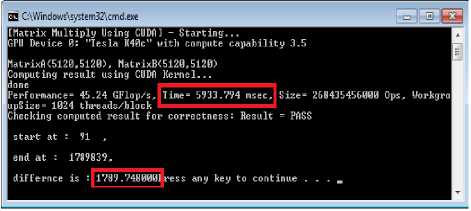
Fig.7. Output screen in CUDA (GPU+CPU) execution

Fig 8, clearly showing the utilization and processing time for only GPU device for all matrix multiplication operations. After evaluation, we can say that GPU performance is better than CPU with difference of millions of seconds. It provides us strong facts to emphasize on increasing the processing power on CPU in order to accomplish better performance.

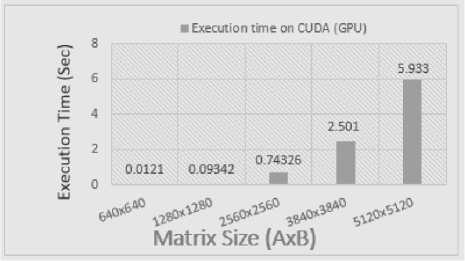
Fig.8. Matrix Multiplication using CUDA (only GPU)

Furthermore, results in figure 9 are giving positive aspect to consider parallel programming models as hybrid in order to achieve HPC. The operation used in our experiments might be smaller as compared to other massive level computation requiring problems such as Computational Fluid Dynamics (CFD) [24], Cholesky decomposition [25], LU complexity operation [26] etc and many more in different fields.

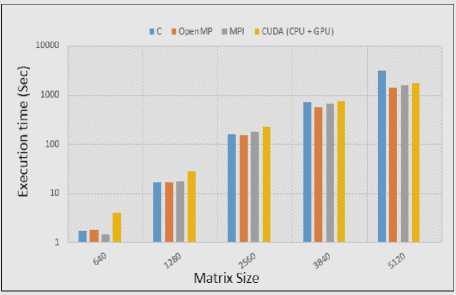
Fig.9. Matrix Multiplication in all programming models

• A. Hybrid Parallel Programming Model

A hybrid approach as (Message Passing Interface and Inter-node parallelism) apparent a promising path to accomplish the exascale computing system [23]. In further our experiments, we evaluated the performance by computing the same mathematical operation through hybrid approaches as discussed below.

OpenMP + MPI and OpenMP + CUDA

Hybrid parallelization approaches permit us to take advantage of the new generation parallel machines possessing connected SMP nodes [27]. In this section we computed the same computational operation on two hybrid approaches. Firstly we evaluated operation by combining OpenMP with MPI messaging passing that employs both shared and message passing between multiple cores. Second hybrid approach was combining OpenMP with CUDA to parallelize the code at both CPU and GPU level. In Results shown in figure 10 shows, second hybrid approach is through very slow in performance than all the approach except simple C++. In contrast, the first hybrid approach is much faster than even single CUDA and OpenMP. For OpenMP/MPI there is no a massive level difference at small level of computation but its shows a clear difference among all other approaches when we compare at large matrix size.

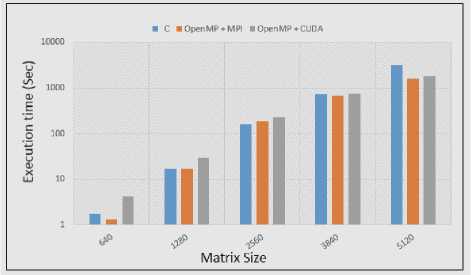
Fig.10. Matrix Multiplication with Hybrid Models

• VII. Conclusion

In order to HPC analysis, we made an empirical analysis of three parallel programming models as (CUDA, MPI and OpenMP). We used matrix multiplication as an operation and computed on parallel programming models. With variation in matrix size, we evaluated the results by parallelizing the code using these parallel programming models. We also evaluated the results by computing matrix multiplication operation in simple Visual C++ language. From the results, we found OpenMP as fast execution model than others. After OpenMP, MPI gave better results as compare to visual C++ and CUDA.

Use of CUDA for a smaller computation operation is costly as compare to all other models including C++. But when we computed high level of matrix multiplication operation, there was an extensive variation in results in all models. We also evaluated the processing time of GPU device excluding CPU interaction that was very small even in Mili-Secs. Further we computed the same mathematical operations using hybrid approaches including CUDA + MPI and CUDA + OpenMP. The execution time in hybrid approaches was half in difference from previous results found in single programming model.

By future perspective, as we noticed GPU device took a very small time of execution but the communication overhead between CPU and GPU effect overall performance. By minimizing this overhead, we must consider more hybrid parallel computing dual-level and tri-level approaches in order to achieve HPC parallelism.

Acknowledgment

I would like to say thanks to Professor Fadi Fouz from King abdulaziz University Jeddah KSA, for teaching the advance stuff related to latest technologies and Professor Fathy Alboraei Eassa for supporting and giving me access of high performance machine to accomplish the work.