Energy and Region based Detection and Segmentation of Breast Cancer Mammographic Images

Breast cancer screening is vital to detecting breast cancer. The most common screening methods are mammography and sonography. Compared to mammography, breast ultrasound examinations have several advantages. Detection and diagnosis of breast cancer in its early stage increases the chances for successful treatment and complete recovery of the patient. Finding an accurate and efficient breast region segmentation technique still remains a challenging problem in digital mammography [1]. Image segmentation is an important research field in medical image processing. Image segmentation is the problem of finding distinct regions that are uniform with respect to certain image features in given images. It allows clinicians to visualize organs and structures in the body, analyze the shapes and sizes of these objects, and diagnose pathologies more quickly and accurately. Segmentation is required as a first step to shape analysis and other medical research objectives. Specifically, we developed and tested this method to segment breast cancer images. The rest of the paper is organized as follows. In Section II, the brief description of related work is presented. Subsequently in Section III we introduce and discuss region based active contours to give a background on the methods that our algorithm incorporates. Section IV reveals the proposed hybrid energy and explains how and why it works. Section V includes results on medical images and compares them with standard energy and region based flows to show the improvements afforded by this algorithm. Finally, we have drawn concluding remarks and discussed the benefits, drawbacks, and potential for future work in Section VI.

• II.    Related work

In image segmentation, energy and region based detection methods are used, where the shape to be recovered is captured. Active contour methods begin with a preliminary curve and characterize some energy for that curve based on its geometric properties and the associated image data. Energy based on the geometry is provided to keep the curve smooth, and energies based on the image data are intended to attract the contour to object boundaries. This curve is then deformed in order to increase or decrease that energy thus moving the curve toward a local maxima or minima. There are many advantages of region-based approaches when compared to edge-based methods including robustness against initial curve placement and insensitivity to image noise. There have been several methods in the literature which are relevant to the present work. Paragios et al. [2] presented a method in which edgebased energies and region-based energies were explicitly summed to create a joint energy which was then minimized. Image segmentation is an important problem in image analysis which is to partition a given image into disjoint regions. There are a wide variety of approaches to the segmentation problem. One of the popular approaches is active contour models, also called snakes. The basic idea is to start with a curve around the object to be detected, the curve moves towards an “optimal” position and shape by minimizing its own energy. Based on the Mumford-Shah functional [3-5]

for segmentation, Chan and Vese [6]. Proposed a new level set model for active regions to detect objects whose boundaries are not necessarily defined by a gradient. To overcome the close boundary initialization problem, many contour-based methods, including Chan and Vese [6], Li and Yezzi [7], Bresson et al. [8], An et al. [9], have been proposed based on Mumford-Shah formulation [3]. Contour-based information helps to overcome local minima and in some case achieve a globally optimal solution regardless of the initialization. Bresson et al. [8] introduced a fast method for global minimization of active contours by combining variational image segmentation and denoising methods. An et al. [9] proposed to use a זconvergence approximation for a multi-scale piecewise smooth model to overcomes the limitations of global contour models while avoiding the high sensitivity of local approaches. Other researchers, including Cremers et al. [10] and Leventon et al. [11], proposed to utilize the shape prior to find a globally optimal solution, given the statistical shape prior is available. It is difficult to segment image with complicated intensity distribution condition, or an inherent complexity in the object present in the image. Generally only one or two level set function are used to segment an image into region of two or more phase. If we use more level set function to segment complicated image into more regions, the dependency of the segmentation result on the initial condition is even more serious. In this work, we address both aspects of variation image segmentation and introduce an efficient and flexible numerical framework that enables us to compute a large class of advantageous descent directions. It has the following key features:

• •    Spatial adaptively: We preserve a common representation of the shape, where resolution is not needed, and a fine revelation with higher node density, where the shape varies more. This is very advantageous for both accuracy and efficiency.

• •    Discretization with predetermined elements: The geometric associations and the resulting partial differential equations are discredited using the predetermined element method. This results in well-defined linear systems, which can be solved efficiently. The discretization is inherent; it does not depend on a parameterization of the shape.

With the new approach, we can automatically segment medical images and produce good segmentation result.

• III.    BACKGROUND

Li et al [12] proposed a method to overcome the difficulties caused by intensity in homogeneities; they propose a region-based active contour model that draws upon intensity information in local regions at a controllable scale. A data fitting energy is defined in terms of a region and two fitting functions that locally approximate the image intensities on the two sides of the region. This energy is then incorporated into a variation level set formulation with a level set regularization term, from which a curve evolution equation is derived for energy minimization. Due to a kernel function in the data fitting term, intensity information in local regions is extracted to guide the motion of the region, which thereby enables our model to cope with intensity in homogeneity.

Energy criterion

Е(0) = ^/д SnKo (х - у) |/(у) - Д (x)Ptf(0(x))dydx +А2/д /д Кс (х - у) |/(у) - £(х)Р (1 - я(0(х))) dyd, +v Jfl 5( 0(x))||V0(x)||d, + я/д ; (HV0(x) II - I)2

Where I(x) is the image intensity at pixel x, H is the

Heaviside function, ку is a Gaussian kernel defined as:

kgljl) =

1 Ыг/

--^е" ^=

(27Г)2*Т”

With a scale parameter и > 0. Д and Ti are two functions centered at pixel x and computed at each iteration as:

^   kff*(H(0(x))/(x))

k_c*(i-HW№^ к^(1-Я(0Сх))

^1 and Я 2 are two constants that have been set to 1 in the interface. The two first integrals of correspond to data attached term, which are localized around each point x thanks to the Gaussian kernel ^^7 . The third integral corresponds to the usual regularization term that smoothes the curve during its evolution. The last integral is a regularization term that forces the level-set to keep signed distance properties over the evolution process.

y(x) = 5(0(x))(Aj

Evolution equation

ка (г - у) |/(у) -A(r)Pdy

+ ^-z/д fcff Сг - у)1/(у) - f2Cr)l3dy + V s(0Gr))к +ЯР2 0to - к)

The parameter ^1 and Яд have a fixed value of 1. Lankton et al [13] proposed a natural framework that allows any region-based segmentation energy to be reformulated in a local way. They consider local rather than global image statistics and evolve a region based on local information. Localized regions are capable of segmenting objects with heterogeneous feature profiles that would be difficult to capture correctly using a standard global method. They describe this framework and demonstrate the localization of three well-known energies in order to illustrate how our framework can be applied to any energy. Improvement can be achieved by comparing with its global counterpart.

Energy criterion:

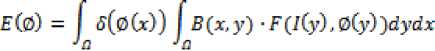
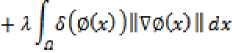
travel along the normal. It also becomes smaller as the curve approaches a boundary.

Where 5 is the Dirac function, B is a ball of radius r centered at point x and defined as follow:

• IV.   proposed algorithm

  

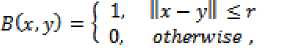
  and

  
  

According to li et al [12] we find the property of the localization introduced by ■Я л and Яд and , fcy . this algorithm is able to segment inhomogeneous objects

F(/(y),0(y)) =                                      лf я(0(у))(/(у) - vGO)2 + (1 — Я (0(y) )} (/(у) -uGO) ( (rW - uGr))2

Where яthe Heaviside is function, uM and pU) are two functions updated at each iteration as follows:

?сВ(л,у) ■ (1 - Я(0(у))) ■ /(y)dy“        /ti SGr,y) ■ (1 - Я(0(y)))dy

JflB(x,y) • Я(0(у)) ■ /(y)dyv fa В Gr, y) ■ H(0(y))dy

The first integral of corresponds to a data attached term and the second is the usual regularization term that smoothes the region.

Evolution equation

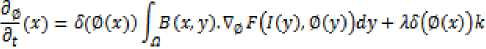
•5(0C>9)CC/C>O - "to)2 - Oto -uto)')

^^Uvm

^            \

(Z(y)-uC*))² ^

and segments the whole image. 0 is a signed distance function.

This algorithm has three specific parameters that can be modified from the corresponding panel:

• •    The curvature term : it weights the influence of the regularization of the evolving region (default value is set to 0.005).

• •    The level-set regularization termДО : it weights the influence of the regularization of the shape of the level-set (default value is set to 1).

• •    The variance of the Gaussian kernel и (default value is set to 7).

Lankton et al [13] suggested an algorithm that is a region-based method and its feature term is computed locally. This property allows the algorithm to segment non homogeneous objects. However this makes the method sensitive to initialization and o is implemented as a signed distance function and is reinitialized at each iteration.

This algorithm has four specific parameters that can be modified from the corresponding panel:

Where A, and -^u are the area of the local interior and local exterior regions respectively given by

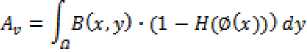
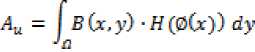
This can be positive or negative depending on the image data. This provides the direction for the curve to

• •    The feature type: the user can choose between Yezzi or Chan & Vese feature type (see equations (7), (12)).

• •    The neighborhood type: the user can choose between a circle or square neighborhood when computing the local statistics.

• •    The curvature term ■■"ⁱ- : it weights the influence of the regularization term of the evolving region (default value is set to 0.2).

• •    The radius term r: it allows to fix the radius size of the neighborhood defined by B (default value is set to 9).

Key to our method is the notation of the probabilitymap F(x) derived from the original image I(x), so that F(x) has larger values at the features of interest. For instance, if we are interested in the image edges, we can use a norm of the image gradient as a probability-map:

FG1 ^W(x)PIW(x)P

This notation is similar to the snakes' external energy ,the higher probability areas of F(x) represent the desirable segmentation regions .We represent our active region , as a mean curve of the probability density function p(x):

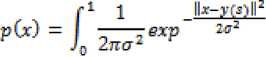
P(x) can be seen as a continuous analog of Gaussian mixture model with equal isotropic co variances. We also add one more term to the p(x), a uniform distribution 1/N (where N is a size of the image domain), in order to account for noise and outliers. We rewrite

p(x) as:

Parameter w represents the contribution of the uniform distribution (0 < w < 1).

We search for the active region position, such that the distribution p(x) maximally approximates F(x), by minimizing Kullback-Leibler (KL) [14] divergence between the distributions:

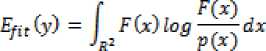
Which we call the fitness term. To regularize the shape of the region we keep the region regularization:

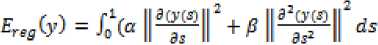
Which we call the regularization term. The goal is to find the function y(s) that minimizes the energy functional:

E(y) = Efty) + £reg(y) . (19)

The influence of each term is controlled by the weights α and β. We note that the probabilistic approach to active regions in Blake and Isard [14], where the mean curve is used to regularize the possible active region shape.

• V.    Experiment simulation and result analysis

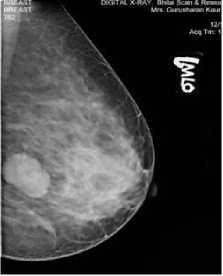
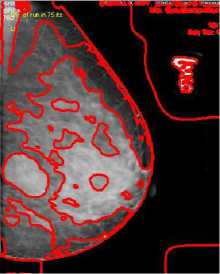
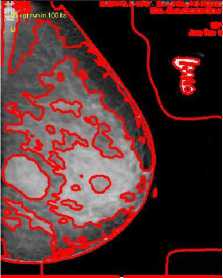
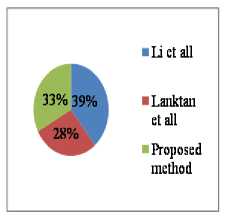
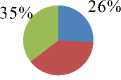
The objective of the proposed algorithm is to achieve robust and accurate segmentation in images by combining maps with regions. We implemented the algorithm in MATLAB, and tested it on a Pentium4 CPU 3GHz with 1GB RAM. We show performance of the method on several real images with average size of 150 *150 pixels. In this experiments, we used α = β=1and also set the weight w of the uniform distribution term equal 0.1 to 0.9. The algorithm requires about 100 iterations to converge. We initialized the active region from the object. First, the active region converges to the mean of the probabilitymap. As we set to α, the active region enlarges to approximate the probability-map for a given scale α. As α decrease the active region achieves the optimum of its energy functional when it lies at the highest nonoverlapping areas of the probability map and the curve produced by the active region is short and smooth. The active region does get attracted to the strait lines, but the shape regularization constraints forces to choose the smoothest and the shortest match. Here, we set β=5 to add some rigidity to the active contour. The active contour segments the boundary accurately, starting from an arbitrary location. This algorithm picks the smoothest, shortest path with higher probability. We use cost function p(x) to implement a fine search strategy. We start from a large value of and gradually reduce it, tracking down the optimum. It does not guarantee to find the global optimum of the function, however empirically the optimum found is within a few percent from the global optimum. In the limit, when и →0, it divergence converges to the conventional external energy term of active regions. In figure 1, shows the segmentation of breast cancer images. For performing the comparison we used MSE and SNR parameter. Mean square error (MSE) is the cumulative squared error between original and resulted image. Signal-to-Noise-Ratio (SNR) measures are estimates of the quality of a reconstructed image compared with the original image. Experimental results show that our proposed method yields significantly improved visual quality as well as better SNR compared to the other techniques in the denoising. But in this approach our proposed method has better SNR and MSE to that of Li et. al [12] but less than that of Lanktan et. al[13] which are shown in Table I, and figure 2. In region-based segmentation methods the energy function depends on all image information, and thus operates on a global image scale. From this perspective, our method is global, because the fitness term depends on all image pixels and thus the method is not simply edge-based [16-18]. Experimental results have demonstrated the advantages of our method over several well-known methods for image segmentation.

TABLE I. P eformance evaluation using sttatictical PARAMETERS

S.No.	Method	MSE	SNR (dB)
1	Li et al. [11]	192.87	15.314
2	Lanktan et al. [12]	138.65	22.759
3	Proposed method	162.34	20.976

(a)

(b)

(c )

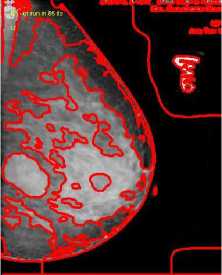
(d)

Figure 1. Segmentation of Breast cancer images (a) Original image; (b) Result of Li et al.[12]; (c ) Result of Lanktan et. al[13]; (d) Result of proposed method

■ Li et all

(a)

39%

■ Lanktan et all

Propose d method

(b)

Figure 2. Comparison of the methods using (a) MSE (b) SNR

• VI.  Conclusion

This paper introduces a novel method for image segmentation based on the region approach that draws upon intensity information in local regions at a controllable scale. The probability density function is derived from the image. The advantage of the divergence function is that it requires all regions of the probability-map which to be approximated by probability-map values makes a region to account for all image regions. We do not need to smooth the initial image, even if it is very noisy and in this way, the locations of boundaries are very well detected and preserved. The segmentation performance will still depend on the accuracy of feature-map construction, but less heavily comparing to the conventional active regions. With this approach we can automatically segment complicated medical images and obtain good final segmentation result.

Acknowledgment

The authors extend their sincere thanks to Dr. Dilip Soni, a senior radiologist at centre for cancer research and diagnosis, Chhattisgarh, INDIA for providing necessary support and guidance throughout the research work.