Energy efficient dynamic bid learning model for future wireless network

As a result of the effects of climate change, which is necessitating energy conservation, energy efficiency is quite crucial for any future wireless network. Hence, this work proposes an energy efficient auction model for future wireless network. The idea behind the proposed model is an automated auction process, which would not always require much input from the users such as the proposed auction model in [19, 20]. Furthermore, in the proposed model in [21], which proposed an auction process for DSA, it was evidently shown that the use of software would be an advantage and it should be adopted in generating the bids during an auction process. This paper proposes the use of learning algorithms to aid the auction process. This is necessary because, in the proposed model in [22, 23], the auctioneer assumed a prior knowledge of the bid equation. However, these assumptions cannot always be made in real systems, because the auctioneers are most likely going to be unaware of the number of the interested bidders until the process of bid submission has been accomplished. Therefore, such an assumption cannot always be generalised. In addition to this, this work adopted the use of an automated software system because most users lack the global knowledge of a wireless network such as the amount of radio resources needed. Therefore, in this work, we propose the use of artificial intelligence. In this model, the users learn how to bid effectively and be able to win the future bidding process using the information available after each auction process. This process is also referred to as machine learning. The use of Machine learning during an auction process helps in eliminating the additional delay that might be introduced into the system as a result of periodic the auction process in dynamic spectrum allocation. This is because the reality is that an auction process requires some time to process the submitted bids and to determine the winner(s). However, delay is an important metric in wireless communication. The delay tolerance of a system depends on the application. A data packet based communications system has more tolerance for delay when compared with the voice communications system.

In this work, we propose a model for DSA using a concept which is based on the first price auction and the use of a reserve price. The reserve price is introduced based on the advantages of the reserve price as outlined in [24]. At the start of an allocation period, a first priced auction process is carried out. In this auction process, each of the user that wants to access the radio spectrum submit a bid and a number of users which is same as the number of channels that is available emerges as the winners. The auction process is explained in more details in the modelling section. Hence, it is a multi-winner auction process. We assume two types of users; those that bid myopically are one group of users while the other group of users are the learning users. A learning user learns the appropriate bid that is above the set reserve price, which is set by the Wireless Service Provide (WSP) using artificial intelligence. Myopic bidders, however places a bid value randomly. The process of setting the reserve price is explained later in the modelling section. Two types of learning methods are examined in this work while examining the delay associated with each model. This paper also compares the amount of energy that is consumed when the users are learning with the non-learning users. This is examined based on Q reinforcement learning and then Bayesian learning used in conjunction with the Q reinforcement learning.

The rest of this paper is as organised as follows: Section II provides the related work. In section III, the energy model, utility function and learning models used in this work are introduced. In Section IV, the simulation model adopted in this work is explained. Results and discussion are provided in section V which is followed by the conclusions in the last section.

• II.    Background and Related Work

Reinforcement learning (RL) is a type of machine learning that allows software agents to learn the ideal behaviour within a context [25]. It uses feedback from the stochastic environment during the learning process to maximize performance by balancing between conflicting considerations [26]. Generally, RL process uses a form of additive reward and penalty. This reward and penalty are sometimes with a discount factor as proposed in [27]. Its learning process involves trials known as an exploration for the learning process to converge effectively before the process of exploration, which is the use of the learnt values. The learning agent usually uses the set of information learnt at time t based on an action a_t ( a_t ∈ A ( S_t )) to transit from one state (S) to another at time t + 1. A learning agent receives a reward ( r t ) based on the action taken. The goal of the learning agent is to derive a maximum possible reward (π : S → A ) form the action taken. Where A ( S_t ) and π is the number of available actions at time t respectively. Reinforcement learning was previously used in [28].

An auction process for dynamic spectrum access was considered in [15]. For a DSA model based on an auction process, learning of the appropriate bid value is rather essential than a user guessing a value because the load on the wireless system varies and the budget of users also varies therefore, if users can learn the appropriate bidding price based on the traffic load, then the users are able to maximise whatever the available budget is by bidding at periods only when the user can afford to pay. This helps to reduce the amount of the energy that is wasted when bids are rejected.

• III.    The Energy Model, Utility Function and Learning Process

• A.    The Energy Model

The energy model adopted in this work is represented using state 1 to 4 as shown in Fig. 1 and explained below:

• 1.    A user with packets to send wakes up into the OFF state, such user subsequently submits a bit to the auctioneer.

• 2.    A winning user changes into the ON state from the OFF state.

• 3.    Such a winning user is in the ON state until after transmission or until when the packet of the user is dropped. Packet dropping is usually as a result of the bid being below the minimum price set by the auctioneer or due to poor channel conditions.

• 4.    The transmission process is completed by the user moving back to the OFF state.

• B.    Utility Function

The utility function expresses the satisfaction derived by the user in placing a bid. The users are assumed to be price sensitive hence, it is in the best interest of the users to win with the least possible

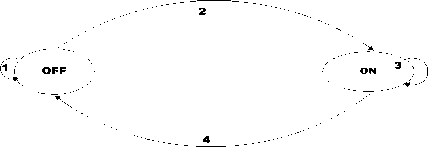
Fig. 1. Energy and system model as a two state Markov chain amount. An exponential utility function is assumed due to its characteristics of an increase, which is rapid in nature. A user whose bid falls short of the reserve price has a utility with a value of zero while the winning user with the least value (bmin) has the highest utility value.

ь^~ 1 If a bidder wins и,(Т> 20™-1

.

0 otherwise

• C.    Q Reinforcement Learning

Reinforcement learning is one form of the several machine learning techniques used in wireless networks [1]. In reinforcement learning, the players involved use a wide range of methods to draw on the prior experience. The policy adopted by the player usually affects the converging speed at which the users learn. Q reinforcement learning, is a kind of reinforcement learning which assigns values to pairs of the action state which is usually used to model Markov decision processes (MDP). Every state has a number of possible actions and the reward earned depends on the action taken (Scalar reward). The reward is based on how close the action is to the best action. Therefore, a temporal difference is used to estimate the optimal value. Take for example, in an auction process with reserve price where users want to win with the least possible amount. The closer the user’s bid is to the reserve price the higher the user’s reward. In a bidding process with reserve price the acceptable values of the winning bids can be any value till above the reserve price and a difference in price unit as small as 0.01 can make a difference between a winning bid and the loosing bid.

The Q reinforcement learning approach used in this work is similar to [10]. This work assumes that the only information held by the users is the information about their own bid history. They do not have the bid history of the other user in the system. It is also assumed that a user can only submit one bid in a bidding round. We also use a first price sealed bid auction with a reserve price. It is assumed that the users in the system have no prior knowledge of the reserve price. This is determined by the WSP according to the process explained in [29].

In the proposed model, a bidding user submits a bid to the spectrum broker who is also the service provider. Based on the bid submitted, the user obtains a utility value using the utility equation (1). It is assumed in this paper that users want to win the auction process with a high value of utility. however, , the closer the user’s bid is to the reserve price the lesser the probability that the user wins the bid therefore, the challenge faced by the bidder is to decide the appropriate value of utility that allows the bidder to be among the winning bidders.

The objective of the learning user is to obtain and optimal π* that maximises the total expected discounted reward given by

V" = E

Ш----<г- v t=0

-*]•

Where E is the expectation operator, 0 ≤ β < 1 is a discounted factor and π is a policy S→ A For a policy π a Q value is defined as the expected discounted reward for executing a at state s and the following policy π is given as:

QK(s,a) = R(s,o) + P

У Prs,s*(o)V7t(s*).

Z_! s.

Where R ( s , a ) is the old value of the Q value. It can be clearly seen from equation (2) to equation (3) that in order to obtain the optimal policy π*, the information of s is vital. In this work, in order to simplify the learning process, we assume that users can only pick a specific bid value form a bin and each bin is associated with a traffic load. Each bin has a range of values as explained further in the modelling section. We associate with a traffic load because the reserve price depends on the traffic load in the system and the reserve price determines if the bid is accepted or rejected. Ideally in a real world the bid value in each of the bins could be associated with the quality of service that the user expects from the WSP. During an exploration period, each user explores a range of available bid values and keep a record as shown in Eq.(4)

Вр = (bj,Nt,u,Nw,W%,Nm ).

Where b j is the j^th value of the bid in the p^th bin, N t is the number of trial with a maximum value of τ, u is the utility derived from the bid value using equation (3), N_w is the number of times the user used the bid value and wins, W % is the winning percentage of the user when using the specific value and N m is the multiplication of W %„ by u . N m is then subtracted from N ^ . Where N ^ is the optimal reward function. The final reward used in updating the Q table is given as

P/]   1   2   3   4-

1   X11  X12 X13  XM-

2    X21  X22 'x23    X24

• ■                      ■                     ■                 ■                         ■.

P    ^Xpi  ^Xp2 ^Xp3   ^Xp4   ^Xpj

Where x_pj the value of N_m of bid j in bin p . During the Q exploration period, the user first try all the available values in all the bins by setting τ to a low number and the user does not try bins in which all the available range of values gives W _% of zero. This is to reduce the exploration period. Take for example, when j = 5 and p = 5. In the tuple below, where the reserve price is assumed to be varying between 4 and 4.5.

? ! = [1, 1.5, 2, 2.5, 3] ?₂ = [3.5,4,4.5,5,5.5] .

At the beginning of the exploration period when τ is set to 10% of maximum τ. The N in the record m for P are all be zero while some of P would be zero and others would have different percentages based 12

on the reserve price. In such scenario, the user would not further explore the values in P 1 .

The Q Reinforcement Learning Algorithm

• 1:    Users pick a bid value randomly from the bin;

• 2:    The utility function of the user based on the bid is calculated;

• 3:    Other record is also calculated e.g W _% and N_m;

• 4:    After 10% of τ trials, the user would try from only bids from bins that are more than 20% and has a value of W > 20;

%

• 5:    After τ trials the user picks the value that gives max W .

%

D. Bayesian framwork for Rainforcement Learning

Delay is a critical factor in a communication network, depending on the application. The delay associated with random exploration in Q reinforcement learning sometimes leads to a convergence – 118 – point that is not optimal. A non-optimal convergence point can be arrived at if the exploration period is not long enough. Hence, there is a need to enhance the exploration process in Q learning. One method that could be used in enhancing Q learning approach is the Bayesian learning. In Bayesian learning algorithm, the learning agent makes a decision based on the most likely event that is going to happen using prior experience. This allows for a faster and smoother movement from exploration behavior to exploitation behavior. Bayesian learning uses the Bayes’ theorem in the exploration stage as shown below.

Р(А\^) = ^(№№ v J P(B)

Where P ( A ) is the prior probability distribution of hypothesis A , the P ( B ) is the prior probability of the training data B and P ( B \ A ) is the probability of A giving B . Bayes learning is appropriate for bid learning because usually a commodity on sale would have a guide price and buyers offers a bid not too far away from the guide price. It also offers several advantages over the Q learning model. Firstly, it provides an ideal format to reach a compromise between the exploration and the exploitation stage by giving information on states in which the player might not have explored. Secondly, it allows an incorporation of the prior determination of the user’s transition. However, it has a disadvantage, which is, it can only be applied when prior information is available.

The prior knowledge used in this work is generated by the system based on previous experience. This is similar to what is adopted in [11]. We assume that the transition matrix is sparse, as only a certain number of the bid values in the bins are non-zero. Similar assumption was made in [11]. The posterior distribution represents the uncertainty in the system, for the transition probability for each of the state action pair, as explained in the Q reinforcement learning.

The Bayesian Learning Algorithm

• 1:    Prior probability is given for all the possible state;

• 2:    Q reinforcement learning is carried out;

• 3:    Bayes rule is applied;

• 4:    Users pick the action with the highest utility and winning percentage.

• IV.    Modelling

In order to evaluate the performance of the proposed learning algorithms, we model a bidding scenario using a multi winner first price sealed bid auction with reserve price similar to [4], where the spectrum is allocated dynamically. We model an uplink scenario with one WSP and N users and M available channel in each of the cells. The users require a transmit channel in order to transmit data files via a central base station. We assume the users are connection oriented and the user to whom the channel is allocated uses the channel for a fixed period of time, before releasing it and another auction round is carried out. We assume a Poisson arrival process with z users out of the N possible users requesting for a channel by submitting a bid ( b ₁, b ₂, b ₃ … b_z ) and the value of z varies depending on the traffic load on the system. The bid value is chosen randomly from the possible bid value in the bin. Based on the bids submitted, K winners which is the number of available channels in the system at time T emerges.

K — Z — N.(8)

The user is allocated the channel, provided the value bided is above the reserve price. The reserve price is dynamic depending on the traffic load and it is calculated by the WSP as shown below.

C_f

T = —,

M ,v)

Cf=^.(10)

Where M is the total number of channels in the system. After submitting the bid the learning process as explained earlier begins. We assume only one of the user is learning to win the bid with the minimum possible amount and others are just bidding myopically. The system flow chart is as shown below (Fig. 2).

• V.    Results and Discusion

The parameters used in the modelling is given in table 1. The reserve price is set in such a way that it varies within a bin depending on the traffic load e.g when the traffic load is 2 or 4 the reserve price can only vary from 0.35 to 0.45 and 0.45 to 0.55 respectively. We also assume all the users are transmitting at the same power and transmission rate.

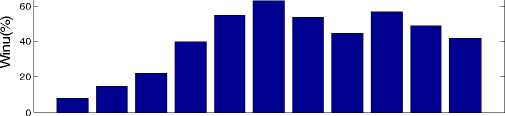
Fig. 3 shows the value of N m in percentage when the traffic load on the system is 4 Erlang and τ is initially set to 500 in then 2000 in Fig. 3(a) and 3(b) respectively. When τ is 500 it can be seen that using a bid value of 50 price unit gives the best value of N m . However, this is not the optimal converging value as it can be seen that when, τ was further increased to 2000 the optimal value changes to 5. With a low value of τ, the learning does not converge at the best value because, utility function and bid acceptance value are like opposing each other. A user bidding the highest value wins, but has a close

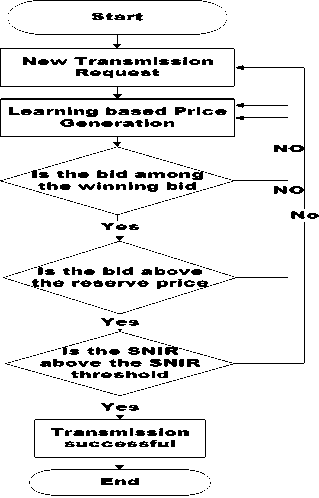
Fig. 2. System flow Chart

Table 1. Parameters Used

Parameter	Values
Cell radius	2 km
SNIR Treshold	1.8 dB
Interference threshold	-40 dBm
Users( N )	50
File Size	2 Gbits
Frequncy Reuse Factor	3
Hight Of Base Station	15 m
Bin 1	[0.30-0.35]
Bin 2	[0.35-0.45]
Bin 3	[0.40-0.50]
Bin 4	[0.45-0.55]
Bin 5	[0.55-0.65]

45     46     47     48     49     50     51     52     53     54     55

(a) Bid Value (Price Unit)

45     46     47     48     49     50     51     52     53     54     55

(b) Bid Value (Price Unit)

Fig. 3. Bid Value for Q Reinforcement Learning with 500 Events and 2000 Events to zero utility value, thereby having a low value of W%. However, as more trial is carried out, this effect balances each other out. It is difficult to know the appropriate value to set τ too but our results showed that when using Q reinforcement learning the value of τ must be sufficiently large enough to allow for optimal convergence.

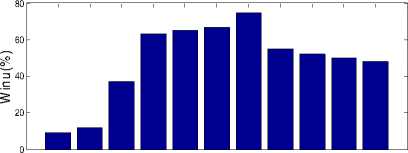
However, using the Bayesian approach with reinforcement learning allows for faster convergence as it can be seen from Fig. 4 that the optimal convergence point is same for when τ is 500 and 2000. This shows that the Bayesian approach to reinforcement learning converges faster than traditional Q reinforcement learning.

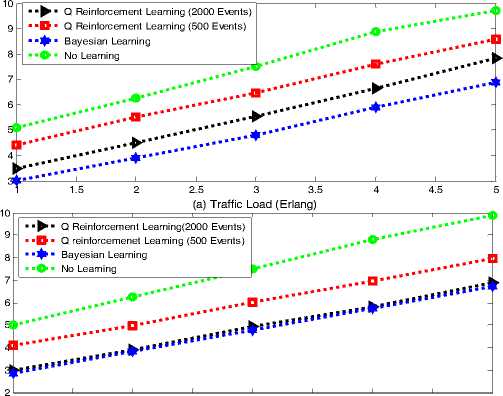
We observe the system performance in terms of the amount of energy consumed per file sent by the learning user and the users that are not learning. Fig. 4(a) shows the results for the warm up stage and Fig. 4(b) for steady state scenario. The warm-up scenario involves both exploration and exploration

45     46     47     48     49     50     51     52     53     54     55

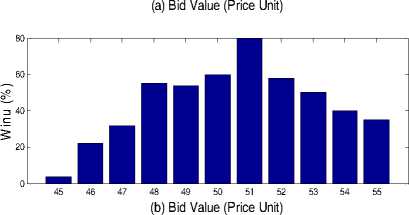
Fig. 4. Bayesian Learning for 500 Events and 2000 Events

1           1.5           2           2.5           3          3.5           4          4.5           5

(b) Traffic Load (Erlang)

Fig. 5. Average Energy consumed for the Learning User while in the steady state the users have finished learning so it involves only exploitation (output from the exploration stage are discarded).

From Fig. 5, it can be seen that the average energy consumed increases with the traffic load in the system because, as the traffic load increases the reserve price and collusion in the system also increases thereby increasing the average energy per file sent. Fig. 5(a) presents the warm up results. Using Q reinforcement learning with 2000 events consumed more energy than 500 events because of the increases in exploration value as it can be seen from 5(b) when the steady state is reached that 2000 events of Q reinforcing learning performs just as good as Bayesian learning but Q learning with 500 events consumes more energy because it does not converge at the best value.

(b) Traffic Load (Erlang)

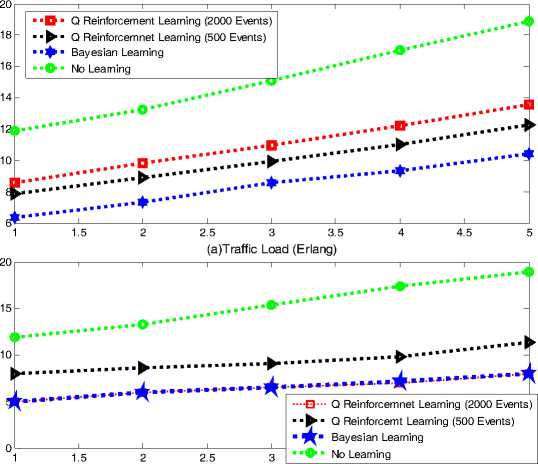
Fig. 6. Average delay for Learning User

Fig. 6 shows the average delay per file sent, with 6(a) being the results from the warm-up stage while Fig. 6(b) is for the steady state. It can be seen that if 2000 events is carried out, Q reinforcement learning perform just as well as Bayesian learning in the exploitation stage, but if we consider the warm-up process, Q reinforcement learning introduces more delay into the system.

• VI.    Conclusions

This paper examines the use of learning based on the auction process for dynamic spectrum access. The paper used the Bayes rule to bias the exploration towards the most promising state, thereby reducing the cost of exploration. The results shows that the use of the Bayes rule helps in reducing the amount of energy consumed, delay and the convergence speed reduction. Q reinforcement learning used in this work is effective and flexible if a large number of trials can be performed, however much faster learning process can be obtained if the reinforcement learning is combined with Bayesian learning.