Enhancement of Hyperspectral Real World Images Using Hybrid Domain Approach

The human eye is a very complex and flexible imaging system which exhibits an enormous dynamic range and can change its sensitivity very rapidly to operate in a large range of light levels, this ability is known as brightness adaption. However the range of distinct intensities that the eye can distinguish at any one time is quite small compared to the total range of intensities that it can adapt to perceive. This means that human eye will struggle to discern very dim intensities when simultaneously exposed to very bright intensities. Unfortunately most artificial imaging systems have a much poorer level of brightness adaption than the human eye and as such can capture a very low dynamic range of intensities [1, 2]. This results in many digital images exhibiting poor contrast either globally or in local regions. There are a number of situations that can result in images exhibiting poor contrast during its acquisitions. Some examples include images captured over a long range through the atmosphere where scattering and aerosols in the air result in the representation of the scene only occupying a small portion of the possible intensity values [2, 3]. A second example is scenes with a very high dynamic range where portions of the image are in shadow and another portion of the image contains very bright information; this is otherwise known as High-Dynamic Range (HDR) images. A third example is in medical scans where information produced by the detectors is very densely packed into the digital image representation [2, 4].

The objective of image enhancement is to improve visual quality of image depending on the application circumstances. Contrast is an important factor for any individual estimation of image quality. Contrast refers to the difference between the highest and lowest intensities used to represent an image. The wider the range of intensity values used to represent the information in an image or area of an image the higher the contrast. Contrast can also describe the distribution of intensity values used to represent the structures in the image. If the occurrences of intensity values are evenly distributed over the entire range of possible values it will be easier for a human viewer to distinguish differing intensities. This is due to the fact that the various intensity levels will be spread further apart and are thus easier for human eyes to tell apart [1, 2,  5]. The contrast enhancement techniques are commonly used in various applications where subjective quality of image is very important. During last decade a number of contrast enhancement algorithms have been developed for contrast enhancement of images for various applications. These techniques are histogram equalization [1], global histogram equalization [6], local histogram equalization [7], adaptive histogram equalization and Contrast Limited Adaptive histogram equalization [8, 9], other histogram equalization based algorithms [10]- [20] and other contrast enhancement methods [21]-[25] have been proposed by various researchers.

The outline of this paper is as follows. Section II describes related research. Section III describes proposed method for contrast enhancement of hyperspectral real world images. Section IV gives simulation results and discussions to demonstrate the performance of proposed method. Finally, conclusion is drawn in section V.

• II.    RELATED RESEARCH

During last decade many techniques have been proposed by various researchers for contrast enhancement of real world scenes for various applications. The simplest technique is to apply an offset and gain to the image intensities based on the minimum and maximum values found in the real world image [2, 6]. This method does improve contrast of most real world images but it is very sensitive to noise and outliers as a single noisy pixel can be found to be one of the extreme values and drastically disturb the scaling [2, 6]. In order to overcome this drawback histogram equalization technique has been proposed and became a popular technique for contrast enhancement. It was initially applied to medical scan images. This technique operates based on the histogram of intensity values of an image. This technique seeks to redistribute the intensities in the image in such a way so that it achieves a uniform distribution of intensities across the entire intensity range [4]. Basic histogram equalization technique is consider the histogram of the entire image in a global fashion, and as such struggles in images where a small portion of the image exhibits a drastically different intensity distribution which would then throw off the equalization for the rest of the image. To struggle this Adaptive Histogram Equalization (AHE) technique was proposed which performed the same process on a per-pixel basis based only on the pixel’s neighborhood. This technique achieves much higher contrast but also amplifies noise, often in an extreme manner [8]. One of the most versatile forms of AHE is Contrast-Limited Adaptive Histogram Equalization (CLAHE) which puts a limit on just how drastically an intensity level can be redistributed. This technique works extremely well on medical images and fairly well on most real-world images. It has the added advantage of being relatively simple and as such has been implemented in a real-time system using specialized hardware [18]. While there has been an enormous amount of research done into histogram based contrast enhancement algorithms, such as [13, 19] they have some drawbacks. These algorithms tend to produce unrealistic effects when they are applied to real-world images.

During past years various researchers have also focused on improvement of histogram equalization based contrast enhancement techniques such as mean preserving bi-histogram equalization (BBHE) [13], dualistic sub-image histogram equalization (DSIHE) [17] and minimum mean brightness error bi-histogram equalization (MMBEBHE) [16]. The BBHE separates the input image histogram into two parts based on input mean. After separation, each part is equalized independently. This method tries to overcome the brightness preservation problem. The DSIHE method uses entropy value for histogram separation. The MMBEBHE is the extension of BBHE method that provides maximal brightness preservation. Though these methods can perform good contrast enhancement, but they also cause more annoying side effects depending on the variation of gray level distribution in the histogram. Therefore, recursive mean-separate histogram equalization (RMSHE) [11] is proposed which provides better contrast results over BBHE. This algorithm is the improvement in BBHE. However, it has also some side effects. In [24] Hassan and Norio is proposed new approach for contrast enhancement using sigmoid function. The objective of this new contrast enhancer is to scale the input image by using sigmoid function. However this method is also have some side effects. In order to improve the performance of above mentioned algorithm another algorithm that is exact histogram specification (EHS) [12] is the method for contrast enhancement of images. In order to provide better result another technique that is brightness preserving dynamic fuzzy histogram equalization (BPDFHE) has been proposed [15]. This technique is the modification of the brightness preserving dynamic histogram equalization technique to improve its brightness preserving and contrast enhancement abilities while reducing its computational complexity. This technique uses fuzzy statistics of digital images for their representation and processing. Therefore, representation and processing of images in the fuzzy domain enables the technique to handle the inexactness of gray level values in a better way which results provide improved performance. In [23], authors proposed contextual and variational contrast enhancement for image. This algorithm enhances the contrast of an input image using interpixel contextual information. This algorithm uses a 2-D histogram of the input image constructed using a mutual relationship between each pixel and its neighboring pixels. A smooth 2-D target histogram is obtained by minimizing the sum of frobenius norms of the differences from the input histogram and the uniformly distributed histogram. The enhancement is achieved by mapping the diagonal elements of the input histogram to the diagonal elements of the target histogram. This algorithm produces better enhanced images results as compared to other existing state-of-the-art algorithms. In order to overcome drawback of above method another algorithm has been proposed in [26]. In this algorithm authors have proposed two stage algorithms for contrast enhancement of hyperspectral real world images. This algorithm consists of two stages: In first stage the poor quality of image is process by adaptive histogram equalization in spatial domain and in second stage the output of first stage is further process by adaptive filtering for image enhancement in frequency domain. The main drawback of this algorithm was to take large processing time. Therefore in order to overcome this problem another algorithm is proposed in this paper. The proposed algorithm works in hybrid domain. The proposed method is efficient algorithm for contrast enhancement of hyperspectral real world images.

• III.    PROPOSED METHOD

The proposed method consists of three phases: In first phase the discrete wavelet transform is applied and approximation coefficient is selected. In second phase approximation coefficient of discrete wavelet transform of image is process by automatic contrast adjustment technique and in third phase it takes logarithmic of output of second phase and after that adaptive filtering is applied for image enhancement in frequency domain. The proposed method is abbreviated as Wavelet based Adaptive Contrast Enhancement (WACE). The model of proposed method is shown in Fig. 1.

Input image [g(x,y)]

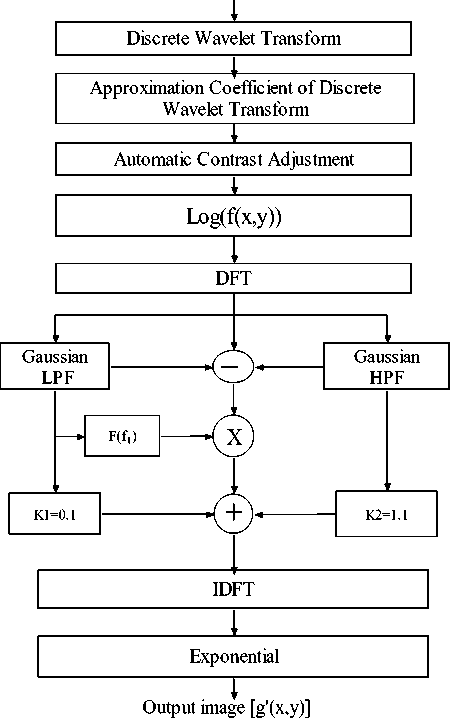
Figure 1. Block diagram of proposed method

• A.    Discrete wavelet transform

A two dimensional discrete wavelet transform provides a frequency band decomposition of the image where each sub-band can be quantized according to its visual importance. Two procedures for performing discrete wavelet transform exist that lead to identical results :(i) Convolution and (ii)Lifting Scheme. The convolution approach utilizes two filters – a low pass and a high pass. The two filters are called analysis filter bank. Inverse discrete wavelet transform also utilizes two filters which are called synthesis filter bank [26]. The two-dimensional discrete wavelet transform can be implemented using digital filters and down samplers and it is shown in the Fig. 2 and Fig. 3, respectively.

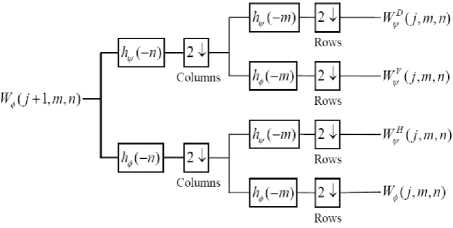
Figure 2. The two-dimensional DWT— the analysis filter

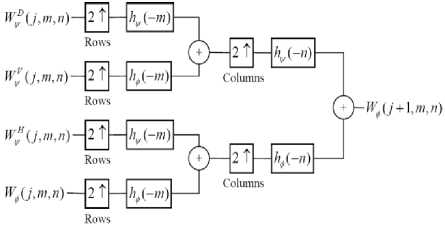
Figure 3. The two-dimensional DWT— the synthesis

• B.    Automatic Contrast Enhancement

It is technique for mapping an image's intensity values to a new range. In this technique the values in the intensity image g(x,y) is transforms to values in f(x,y) by mapping values between low and high to the values between bottom and top [1,5]. The values below low and above high are clipped; that is, values below low map to bottom, and those above high map to top. For example, rice.tif is a low contrast image. The histogram of rice.tif indicates that there are no values below 40 or above 255. If it remap the data values to fill the entire intensity range [0, 255], then it can increase the contrast of the image.

• C.    Logarithmic Transformation and Adaptive Filtering

A two dimensional image is denoted by a function f(x,y). The amplitude off at spatial coordinates (x,y) is a positive scalar quantity whose physical meaning is determined by the source of image. When an image is generated from a physical process, its values are proportional to energy radiated by a physical source such as electromagnetic waves and infrared waves. As a consequence, f(x,y) must be non-zero and finite. The two dimensional function f(x,y) may be characterized by two components: (i)The amount of source illumination incident on the scene being viewed (ii) The amount of illumination reflected by objects in scene. First one is called illumination component and it is denoted by i(x,y) and second one is called reflectance component and it is denoted by r(x,y). These two components are combined as a product to form two dimensional function f(x,y). Therefore it is given by

f(x,y)=i(x,y)*r(x,y)                                     (1)

The nature of i(x,y) is determined by illumination source, and r(x,y) is determined by the characteristics of the imaged objects. The function f(x,y) cannot be used directly to operate separately on the frequency components of illumination and reflectance because the Fourier transform of the product of two function is not separable. However if we define

z(x,y)=ln[f(x,y)]=ln[i(x,y)]+ln[r(x,y)]                  (2)

Then

F{z((x,y)} = F{ln[f(x,y)]}=F{ln[i(x,y)}+F{ ln[r(x,y)]}

The illumination component of two dimensional images generally is characterized by slow spatial variation, while the reflectance component tends to vary abruptly, particularly at the junction of dissimilar components. These characteristics lead to associating low frequencies of the Fourier transform of the logarithm of an image with illumination and the high frequencies with reflectance. A good deal of control can be gained over the illumination and reflectance components by defining a filter function that affects low and high frequency components of the Fourier transform in different ways. The filter function should be such that it tends to decrease the contribution made by the low frequencies (illumination) and amplify the contribution made by high frequencies (reflectance). The net result is simultaneous dynamic range compression and contrast enhancement.

In the proposed method we have suppressed the low frequency components by 92% and increased the clearly visible high frequency components by 115%. Therefore the hidden frequency components are locally enhanced depending on illumination of that particular region. The hidden frequency components are convolved with the function F(f l ) where F is defined as F(f 1 )=1+kf 1

Where the value of k is different for each 17x17 block

Now the modified high frequency components, low frequency components, and hidden frequency components are added together to give new enhanced two dimensional images in the frequency domain. After that inverse discrete Fourier transform is taken to get the enhanced image in spatial domain. Finally, as z(x,y) was formed by taking the logarithm of the original image f(x,y), the inverse (exponential) operation yields the desired new enhanced image.

• D.    Implementation of proposed method

Step1. Read the input image.

Step2. Convert input image into gray scale image if it is color image.

Step3. Apply Discrete Wavelet Transform

Step4. Select Approximation Coefficient of Discrete Wavelet Transform

Step5. Adjust contrast of input image by function imadjust.

Step6. Take logarithmic of result of step(5)

Step7. Find DFT of output from Step(6)

Step8. Perform adaptive filtering for image enhancement.

Step9. Find IDFT after adaptive filtering operation.

Step10. Find exponential of IDFT from Step(9)

• IV. SIMULATION RESULTS AND DISCUSSIONS

  To judge the performance of proposed WACE method, it is tested on different gray scale hyperspectral real world images with dimension Ml×M2 (=512×512) [27]. In order to obtain simulation and experimental results of proposed WACE method and other existing contrast enhancement algorithms are implemented in MATLAB software (MATLAB 7.6, release 2008a). Therefore, two experiments have been conducted on different gray scale hyperspectral real world images. In the first experiment the image quality metrics is presented and in the second experiment visual enhancement of image is presented. In order to judge superiority of proposed WACE method the quality parameters such as measure of enhancement (EME) and measure of enhancement factor (EMF) are the automatic choice for the researchers. Therefore, a better value of EME and EMF implies that the visual quality of the enhanced image is good. The measure of enhancement (EME) and measure of enhancement factor (EMF) are defined in equation (4) and equation (5) respectively. These image quality metrics are used to compare the performance of proposed WACE method and other existing contrast enhancement techniques such as Histogram Equalization (HE), Alpha Rooting (AR) [21], Multi contrast enhancement (MCE) [22], Multi contrast enhancement with dynamic range compression (MCEDRC) [14], Exact histogram specification (EHS) [12], Brightness preserving dynamic fuzzy histogram equalization (BPDFHE) [15], ACEBHE Method [26]. The test real world hyperspectral images used for the experiments are available on the website http://vision.seas.harvard.edu/hyperspec/explorei.html .

The measure of enhancement (EME) [25, 26, 28] of image I(i, j) with dimensions Ml×M2 pixels is defined as: ЕМЕ_к1к2 ^.^^.Ц^)] (4)

where an image (I) is divided into k 1 ×k 2 blocks, I max,k,l and I min,k,l are the maximum and minimum values of the pixels in each block.

The measure of enhancement factor (EMF) between output image and input image is defined as:

ЕМЕ of output image

Ь M г = ------------

ЕМЕ of input image

• A.    Experiment 1

In this experiment the performance of proposed WACE method is tested on different gray scale Hyperspectral real world images. The performance of proposed WACE method and many existing contrast enhancement techniques has been evaluated for image1512, image2512, image3512, and image4512 in terms of quality parameters such as measure of enhancement (EME) and measure of enhancement factor (EMF). For image1512, image2512, image3512, and image4512 the performance of proposed WACE method has been compared with many existing contrast enhancement techniques. The measure of enhancement (EME), measure of enhancement factor (EMF) and CPU processing time of proposed WACE method and many existing contrast enhancement techniques for image1512, image2512, image3512, and image4512 have been given in Table 1. Therefore, it can be noticed from Table 1 that the proposed WACE method provides better results as compared to other state-of-art contrast enhancement techniques such as Histogram Equalization (HE), Alpha Rooting (AR), Multi contrast enhancement (MCE), Multi contrast enhancement with dynamic range compression (MCEDRC), Exact histogram specification (EHS), Brightness preserving dynamic fuzzy histogram equalization (BPDFHE), ACEBHE Method.

• B.    Experiment 2

In order to perform the superiority of proposed WACE method another experiment has been conducted on different gray scale Hyperspectral images real world images.

This experiment visualizes subjective image enhancement performance, the enhanced contrast of image1512; image2512, image3512, and image4512 have been compared with result of proposed WACE method and many existing contrast enhancement techniques. The visual contrast enhancement results of proposed WACE method and many existing contrast enhancement techniques have been given from Fig. 4 to Fig.7. Therefore, it can be noticed from Fig. 4(B) to Fig. 4(I), Fig. 5(B) to Fig. 5(I), Fig. 6(B) to Fig. 6(I) and Fig.7(B) to Fig. 7(I) that proposed WACE method gives better contrast enhancement results as compared to other existing contrast enhancement techniques such as Histogram Equalization (HE), Alpha Rooting (AR), Multi contrast enhancement (MCE), Multi contrast enhancement with dynamic range compression (MCEDRC), Exact histogram specification (EHS), Brightness preserving dynamic fuzzy histogram equalization (BPDFHE), ACEBHE Method.

TABLE 1: COMPARATIVE PERFORMANCE OF DIFFERENT METHODS AND GRAY SCALE HYPERSPECTRAL REAL WORLD IMAGES

Method Parameters	HE	AR	EHS	BPDFHE	MCEDRC	MCE	ACEBHE	WACE (Proposed)
Image1512.tif
EME(Original)	2.47	2.47	2.47	2.47	2.47	2.47	2.47	2.47
EME(Output)	5.56	2.77	5.65	3.36	2.52	3.02	4.89	5.93
EMF	4.27	1.12	3.90	1.36	1.02	1.22	1.98	2.40
CPU Time (second)	0.03	0.38	1.56	0.19	1.77	0.38	0.85	0.55
Image2512.tif
EME(Original)	3.03	3.03	3.03	3.03	3.03	3.03	3.03	3.03
EME(Output)	5.58	3.23	7.34	3.63	3.07	3.67	6.20	8.67
EMF	1.84	1.07	2.43	1.20	1.01	1.21	2.05	2.86
CPU Time (second)	0.04	0.36	1.44	0.19	1.76	0.37	2.72	0.55
Image3512.tif
EME(Original)	3.35	3.35	3.35	3.35	3.35	3.35	3.35	3.35
EME(Output)	9.10	3.67	10.44	3.89	3.38	3.98	7.04	11.61
EMF	2.71	1.09	3.11	1.16	1.01	1.19	2.10	3.46
CPU Time (second)	0.04	0.38	1.55	0.18	1.75	0.38	0.99	0.56
Image4512.tif
EME(Original)	2.58	2.58	2.58	2.58	2.58	2.58	2.58	2.58
EME(Output)	12.08	2.77	16.86	6.05	2.60	3.09	6.59	14.30
EMF	4.45	1.07	6.53	2.34	1.01	1.20	2.55	5.53
CPU Time (second)	0.04	0.37	1.77	0.19	1.76	0.37	0.59	0.55

(A). Original image

(B). Output of HE

(D). Output of EHS

( C ). Output of AR

(E). Output of BPDFHE

(G). Output of MCE

(H). ACEBHE Method

(F). Output of MCEDRC

(I). Output of WACE Method (Proposed)

(A). Original image                     (B). Output of HE                     ( C ). Output of AR

(E). Output of BPDFHE

(D). Output of EHS

(F). Output of MCEDRC

(G). Output of MCE

(H). ACEBHE Method

(I). Output of WACE Method (Proposed)

(A). Original image

(B). Output of HE

(D). Output of EHS

( C ). Output of AR

(E). Output of BPDFHE

(F). Output of MCEDRC

(G). Output of MCE                 (H). ACEBHE Method           (I). Output of WACE Method

(Proposed)

(A). Original image                        (B). Output of HE                     ( C ). Output of AR

(D). Output of EHS                 (E). Output of BPDFHE            (F). Output of MCEDRC

(G). Output of MCE                 (H). ACEBHE Method           (I). Output of WACE Method

(Proposed)

• IV.    CONCLUSION

In this paper an efficient algorithm was proposed for contrast enhancement of hyperspectral real world images for various applications. This method was tested on different gray scale hyperspectral real world images. The qualitative and subjective enhancement performances of proposed WACE method was evaluated and compared to other state-of-art contrast enhancement techniques. The performance of proposed WACE method was evaluated and compared in terms of EME, EMF and Execution time. The simulation results demonstrated that proposed WACE method provided better results as compared to other state-of-art contrast enhancement techniques for different gray scale hyperspectral real world images. The visual enhancement results of proposed WACE method were also better as compared to other state-of-art contrast enhancement techniques. Therefore, proposed WACE method performed very effectively and efficiently for contrast enhancement of gray scale real world hyperspectral     images. The proposed WACE method can also be used for many other images such as remote sensing images, electron microscopy images and even real life photographic pictures.