Enhancing Mobile Software Developer Selection through Integrated F-AHP and F-TOPSIS Methods
Автор: Murnawan, Vaya Viora Novitasari
Журнал: International Journal of Information Engineering and Electronic Business @ijieeb
Статья в выпуске: 4 vol.16, 2024 года.
Бесплатный доступ
This study delves into the impact of employee recruiting within the dynamic and fiercely competitive realm of information technology (IT), focusing on the role of mobile software developers in a software development company situated in Bandung, Indonesia. Given that the quality of employees and their alignment with organizational needs are pivotal drivers of productivity and overall performance, the recruitment process assumes paramount importance. However, this process is riddled with complexity and challenges, stemming from the need to define precise criteria and navigate decision-making amidst uncertainty and ambiguity. To confront these challenges, this research advocates for the utilization of the Fuzzy Analytic Hierarchy Process (F-AHP) and Fuzzy Technique for Order of Preference by Similarity to Ideal Solution (F-TOPSIS). The F-AHP method, employing Chang's extent analysis approach, assists in establishing weights for uncertain criteria. Meanwhile, F-TOPSIS is leveraged to evaluate alternatives based on predefined criteria. The focal point of this study is the selection of mobile software developers within a software development company in Bandung, Indonesia. Decision-makers, drawing insights from policy documents and assessment forms, identified pertinent criteria and sub-criteria. Utilizing F-AHP, they determined the weights for criteria and sub-criteria through paired comparisons using fuzzy numbers. Subsequently, F-TOPSIS was applied to rank 10 mobile software developer candidates, culminating in the identification of alternative-7 (CK-7) as the top mobile software developer candidate. In essence, the application of F-AHP and F-TOPSIS methods presents an effective approach to navigate the complexity of Multi-Criteria Decision Making (MCDM) in employee selection, particularly within the competitive landscape of the information technology industry. This study's findings underscore the significance of employing advanced decision-making techniques to enhance the efficiency and effectiveness of employee recruitment processes, thereby bolstering organizational performance and competitiveness.
Employee Selection, Extent Analysis, Fuzzy Analytic Hierarchy Process (F-AHP), Fuzzy Technique for Order of Preference by Similarity to Ideal Solution (F-TOPSIS), Mobile Software Developer Selection
Короткий адрес: https://sciup.org/15019422
IDR: 15019422 | DOI: 10.5815/ijieeb.2024.04.01
Текст научной статьи Enhancing Mobile Software Developer Selection through Integrated F-AHP and F-TOPSIS Methods
Published Online on August 8, 2024 by MECS Press
Employee selection is critical to a company's success and sustainability in the dynamic and competitive information technology industry. Recruiting and maintaining competent workers with the appropriate skills and abilities to manage the complicated and fast-paced sector is critical to increasing productivity and overall performance. However, the employee recruitment is a complex task that requires various factors, such as education background, experiences, and interpersonal skills.
Employee selection is a complex process that involves several challenges. The main challenge is the uncertainty and ambiguity involved in selecting the criteria and weights used to evaluate workers. This can lead to subjective and inconsistent decision-making, which can negatively impact the organization's performance. In addition, when faced with various criteria and choices that demand thorough analysis, humans may fail to make appropriate decisions. Hence, a strategy is required to aid in the definition of precise criteria and weights while enabling effective and accurate decision-making.
This study proposes an integrated approach by combining the Fuzzy Analytical Hierarchy Process (F-AHP) and Fuzzy Technique for Order of Preference by Similarity to Ideal Solution (F-TOPSIS) methods. The concept of fuzzy sets, introduced by Zadeh [1, 2], is applied in the context of Multi-Criteria Decision Making (MCDM) to address the uncertainty and ambiguity in human cognitive processes [3, 4].
In this research, F-AHP is employed using Chang's extent analysis approach (Chang, 1996) to assess the importance of each evaluation criterion. Subsequently, F-TOPSIS is applied to rank employee alternatives for the mobile software developer position based on the criteria weights determined through F-AHP. The integration of F-AHP and F-TOPSIS in this study leverages the strengths of both methods to overcome the challenges of employee selection.
F-TOPSIS is recognized as an easily implementable approach that yields stable results in decision-making [5]. However, a notable drawback is the lack of specific guidelines for assigning weights to each criterion [6]. Therefore, a more systematic approach, such as F-AHP, becomes crucial for determining criteria weights in a more measurable manner.
F-AHP enables the establishment of consistent and reliable criteria weights, accommodating uncertainty and ambiguity through pairwise comparisons between evaluation criteria, whether quantitative or qualitative, using linguistic terms. Nevertheless, the use of F-AHP in isolation can be a complex process, especially with numerous alternatives or evaluation criteria, involving repetitive assessments and quite extensive pairwise comparisons. Therefore, an integrated approach with F-TOPSIS is adopted after the F-AHP process to rank each alternative.
The specific objective of this study, which involves integrating the F-AHP and F-TOPSIS methods for optimizing the selection of mobile software developer employees, is to enhance effectiveness and efficiency in the employee selection process. The aim is to acquire high-quality employees who meet the competencies required by the company. This integrated method is anticipated to address uncertainties or ambiguities in determining criteria and weights, as well as difficulties in making precise decisions when confronted with numerous criteria and alternatives.
Hence, the integration of the F-AHP and F-TOPSIS methods is of high significance in improving the quality of employee selection and the success of companies in the information technology industry. This method supports companies in efficiently and effectively choosing employees who best align with the company's needs, ultimately having a positive impact on productivity and performance in a highly competitive market environment.
Innovatively, this study seeks to enhance the traditional methods of employee selection by augmenting accuracy and efficiency in decision-making processes. By juxtaposing the integrated approach with conventional selection methods, this research underscores the advancements in decision-making precision and efficacy achievable through innovative methodologies.
The research statement emphasizes the anticipated impact of this study, elucidating how this approach specifically enhances the selection of mobile software developers and augments organizational performance. By reinforcing this thesis, the study underscores its contribution towards streamlining employee selection processes and fortifying organizational competitiveness within the IT industry.
2. Literature Review
In 1981, Thomas L. Saaty introduced the Analytical Hierarchy Process (AHP), a decision-making approach that enables the evaluation of alternatives based on quantitative and qualitative criteria structured in a multi-level hierarchy [7]. In AHP, weighted total scores are obtained for each alternative, and these scores are used to determine the overall rankings [8]. To address the challenges of uncertainty and ambiguity in decision-making, AHP evolved into the Fuzzy Analytical Hierarchy Process (F-AHP) with the application of fuzzy logic.
The implementation of F-AHP has been widely used in various Multi-Criteria Decision Making (MCDM) contexts, such as in the tourism sector [5], property development [6], knowledge management in university settings [9], academic research productivity [10], the health sector [11, 12], the energy sector [13], public transportation service quality issues [14], and business and logistics sectors [15, 16].
TOPSIS, short for Technique for Order of Preference by Similarity to Ideal Solution, is a method developed by Hwang and Yoon [17]. The fundamental principle of this method is that the optimal alternative solutions will be closest to the Positive Ideal Solution (PIS) and farthest from the Negative Ideal Solution (NIS). TOPSIS offers several advantages, including ease of use, rational basis, clear understanding, high computational efficiency, and the ability to measure the relative performance of each alternative using simple mathematical formulations.
An extension of this method is the Fuzzy Technique for Order of Preference by Similarity to Ideal Solution (F-TOPSIS), which takes into account the fuzzy aspect. F-TOPSIS has been successfully applied in various evaluation and ranking contexts. For example, F-TOPSIS is used in flood vulnerability mapping [18], determining winners in procurement tendering [19], research on lake ecotourism [20], assessment of improvement strategies for mosque buildings [21], optimization of manufacturing processes in India [22], determination of key performance indicators in human resource management for military hospital managers [23], and human resources selection [24].
The integration of F-AHP with F-TOPSIS has been implemented in various applications, as documented in scholarly literature. In this integrative approach, the initial step generally involves determining the weights of crucial criteria using F-AHP, followed by the evaluation of alternatives using F-TOPSIS with weights derived from the F-AHP results. Several research examples encompass the evaluation of the highly effective security methodology in digital healthcare services by integrating data security with existing management strategies [25], the assessment of suitable fuel-based bus technology in India [26], determining criteria for reducing mercury risks in small-scale gold mining [27], selection of promotional media on tourist ships [6], primary banking system selection [28], prioritizing solutions for historical learning [29], evaluating manufacturing relocation decisions [30], subjective assessment in the selection process [31], military robot usage selection [32], assessing high school performance in the context of group decisionmaking [33], apartment selection model based on design and quality [34], identifying and prioritizing solutions to address overlooked intellectual errors in teaching [29], evaluating and selecting digital marketing technology [35], renewable energy source selection in the Polish industrial sector [36], and assessing and selecting the most effective traffic detection approach for more reliable, efficient, and systematic design [37].
Workforce selection is a domain that frequently utilizes Multi-Criteria Decision Making (MCDM) methods. In a study by Nhu Mai Thi Nong and Duc Son Ha, they applied the TOPSIS method for the selection of qualified employees in the distribution sector [38]. On the other hand, Usluet et al. utilized AHP and MULTIMOORA in the selection of qualified managers in healthcare facilities to achieve objective selection among candidates [39]. Meanwhile, Rahi et al. utilized F-TOPSIS in designing an interview mechanism capable of selecting or ranking prospective employees [40].
Akmaludin et al. utilized the Analytic Hierarchy Process (AHP) and Elimination and Choice Translating Reality (ELECTRE) methodologies to assess the supporting criteria that could function as selection parameters for programmers. The primary objective was to align with industry requirements and make optimal decisions. The investigation considered the integration of multiple criteria, encompassing diverse quantitative evaluations, including those associated with time aspects featuring contradictory characteristics during implementation [41].
Concurrently, Ikah and Fitriani applied the AHP method to identify factors of utmost importance in employee acceptance at PT Citatah Tbk [42]. He, Xie, and Wan combined AHP with Grey Relational Analysis (GRA) to tackle issues linked to the selection of new employees within the technology company context [43].
Danişan et al. conducted research by applying the AHP-TOPSIS approach to select candidates most suitable for the offered job descriptions [44]. On the other hand, Ozdemir and Nalban aimed to find the best employees using the integration of Consistent Fuzzy Preference Relations (CFPR) and F-AHP methods [45]. Lastly, Raj Mishra and his team incorporated the Intuitionistic Fuzzy Additive Ratio Assessment (IF-ARAS) method in their research to select the best IT employee candidates, integrated with divergence measurement, enhanced score functions, and IF aggregation operators [46].
In the literature context, this research is most relevant to the study conducted by Kaya and Kahraman [47]. This research applied the F-AHP method with Chang's extent analysis approach to determine criterion weights. Subsequently, the F-TOPSIS method was used to rank alternatives for the position of mobile software developer candidates.
-
2.1. Fuzzy Sets Theory
The theory of fuzzy sets is a mathematical framework associated with classes that have indefinite boundaries [48]. This concept can be further detailed by developing the idea of fuzzy sets through the generalization of traditional set concepts into fuzzy sets (Ozdemir and Nalbant, 2020). In the context of this research, for the sake of simplicity, the researcher chose to employ triangular fuzzy numbers (TFN) when applying the F-AHP and F-TOPSIS methods. Fuzzy numbers are a specific fuzzy set denoted as F = {(x,nF(x)),x £ R}, where x is a real number, R: — ^ < x < +», and /л F(x ) is a continuous mapping from R to the closed interval [0, 1]. TFN is expressed as M = (I, m, u) with I
and has a triangular membership function as described below:
FfW =
where:
l : the lowest value or lower limit m : the middle value
u : the highest value or upper limit
'0x < 1
x-l
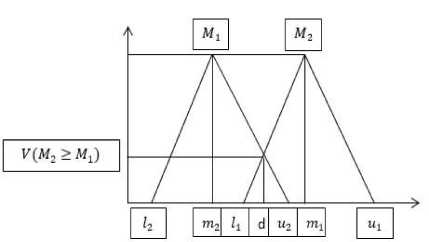
— I -m .0x > и Fig. 1. Triangular Fuzzy Number The basic operations between two positive TFNs are as follows: A = (11,141,111), where 11 < m1 < U1, and В = (l2, m2, U2), where l2< m2< U2, can be described as follows: A + В = (11 + l2, m1 + m2,u1 + u2)(2) A — В = (l1 — I2, m^ — m2,Ui — U2)(3) A* В = (l1* l2,m1 * m2,U1 * u2)(4) '(5) D U2 m.2 A-1 = (-, — ,7)(6) щ_ -m^ li The distance between two positive TFNs A = (l1,m1,U1) and В = (l2,m2,U2) can be calculated using the vertex method, as follows: d(A,В) = ^1(l1—2)2+m1—m2y+^(7) To calculate the response of n decision-makers using the geometric means method based on the following equation: rt = №=1Vt)(8) If M = (l, m, u) is a positive TFN, then M can be defuzzification as follows: M = l + (m-l)+(u-l), Or m = l+4m+u(9) 3 , 2.2. Fuzzy AHP (F-AHP) Method The Fuzzy Analytical Hierarchy Process (F-AHP) method, introduced by Chang [49], is based on the principle of extent analysis. In the context of this research, the initial step involves the implementation of the F-AHP with the aim of identifying significant weights for relevant criteria and sub-criteria. Subsequently, the extent analysis method by Chang is utilized to conduct fuzzy pairwise comparisons between these criteria and sub-criteria. Let = {Xj} dan i = 1, — ,n be a set of elements, and G = {gj} dan j = 1,---,m be a set of goals. Then, the range analysis value for each element is obtained as follows: M1,M2,-,Mm,i = 1,2,-,n (10) All elements of Mg.(j = 1,2, ■ ,m) are TFN. The synthetic fuzzy range value for the i-th element is expressed as follows: -1 Sj = zm=1Mj ® [xf=1Xm=1Mj] (11) To obtain Xjm=1 M^ , fuzzy numbers are summed as follows: V^Mh = [Z7=1^7=1m),X"=1UJ-] Then, to calculate [X^=1 ^>1 M^] , Equations (13) and (14) are utilized. S?=1S7=1M< = (SF=1/f,SF=1mf,SF=1Uf) -1 [£?=1£7=1M<] Z?=1u^,Z?=1m, ,ZP=1Z, If M1 and M2 are TFNs, the possibility degree of M2 > M1 is defined by Equation (15) as follows in the context of this article: V(M2 > Ml) = supy>x[min(pM1(x), pM2(y))] Where sup is the minimal result of the minimal upper bounds of the vector. Equation (15) is equivalent to the following expression: V (M 2 > M1) = hgt ( M 2 П M1 ) = Pm2 ( d ) ^1 if m2 > mx if l > u = s l — U (m2 - u2) - (m{ - 4 ) others If the fuzzy value result is more significant than к, Mt (i = 1,2, _, к) such that the vector value can be represented by the following equation: V(M > M 1,M2,-,Mk) = V (M > M 1) dan (M > M2) dan • - - (M > Mk ) = min V (M > Mz) The defuzzification ordinate is depicted by the following equation: d^A^ = min V (51 > Sk) For к = 1,2, ^ ,п; к ^ i, resulting in obtaining the vector weights as illustrated in the following equation: W' = (df(A1),d'(A2).....d'(An)y Where A^ = 1,2, .^,n is a fuzzy vector (W). The comparison of the two factors used to determine the vector values can be seen in Figure 2. Fig. 2. Comparison Between Two Criteria The degree of possibility for a convex fuzzy number M to exceed к convex fuzzy numbers Mi for i = 1, — ,k is defined as: V(M >M1,M2, — ,Mk=V(M >M1)and(M >M2) and(M > Mk) = minV (M > Mt),i = 1, — ,k(20) The W vector, denoted as W' = (d'(C1), d'(C2), ■■■, d'(Ck))T, is calculated under the assumption: d' (Ct) = minV (St > Sj),i = 1, — ,kj = 1, — ,kk Ф j(21) The normalized W vector, comprising non-fuzzy numbers, is presented as: W = (d(C1),d(C2).....d(Ck),)T(22) The final priority weights are used as a guide to establish the ranking of each element. The computation of the final weights for each criterion takes into consideration the relative importance levels among the criteria. In the context of this research, based on the described extent analysis steps and utilizing the F-AHP approach, significant weights (in the form of the vector W) are obtained for sub-criteria and criteria in each pairwise comparison matrix. Following that, the pairwise comparison matrices undergo fuzzification using Equation (8), and the subsequent calculation involves determining the consistency ratios. Following the extent analysis steps outlined and employing the F-AHP method, crucial weights (represented by the vector W) for sub-criteria and criteria in each pairwise comparison matrix are determined. Following that, the defuzzification process is applied to each pairwise comparison matrix using Equation (8), and the consistency ratio is subsequently calculated. In this paper, using the outlined steps of extent analysis and F-AHP, the importance weights (W vectors) for subcriteria and criteria are determined for each pairwise comparison matrix. Subsequently, each pairwise comparison matrix is defuzzified using Equation (8), and the consistency ratio is computed. Let A be the defuzzified nxn pairwise comparison matrix, and W be the weight vector obtained from extent analysis. By solving the equation AW = Amax, where Xmax is the largest eigenvalue (referred to as the principal eigenvalue), the consistency index (CI) and consistency ratio (CR) are then calculated as follows: qj _ ^max n-1 CR=- RI If the CR is less than 0.10, the comparison is considered acceptable; otherwise, it is not. The Random Index (RI), representing the average index for randomly generated weights, is provided in Table 1 based on the matrix size n. Table 1. Random Index (RI) Matrix Size 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 RI 0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51 1.48 1.56 1.57 1.59 2.3. Fuzzy TOPSIS (F-TOPSIS) Method The Fuzzy TOPSIS method was introduced by Chen [50] as a solution to address Multiple Criteria Decision Making (MCDM) problems under uncertainty. Steps of fuzzy TOPSIS are outlined below, assuming there are m alternatives to rank and n sub-criteria. A fuzzy decision matrix is provided as follows: X1n X2n Xmn- X11 X21 - Xm1 where X^Vi,) represents linguistic variables described by positive Triangular Fuzzy Numbers (TFNs) Xtj = (atj, btj, ctj). The weight vector W = [w1, w2, ■ ,wn\ for n sub-criteria was obtained from the previous F-AHP analysis. Step 1: For I DMs, calculate the aggregated Xtj = 1 [X1j + X^ + —+ X1^ + —+ Xy], where Xtj represents the rating of the kth DM for the ith alternative concerning the jth criterion. Step 2: Construct the fuzzy decision matrix D and the normalized fuzzy decision matrix S. Here, В and C denote the sets of benefit and cost criteria, respectively. where §tj $ = [sij]mxr (,су cy e)’^ ^B;$4 (cij’bu’a^’j^C'' c 1=maxcj,jeB; ai minatpjec. Step 3: Construct the weighted normalized fuzzy decision matrix 1^ = [Vy]xn , where Vtj = stj ■ Wj normalized positive Triangular Fuzzy Numbers (TFNs) with ranges in the interval [0,1]. Step 4: Define the fuzzy positive-ideal solution A+ and fuzzy negative-ideal solution A". are A+ = (v+’^+’-’V^ A" = (V"’V"’-’V-) (27) wherev+ = (1,1,1) and Vj = (0,0,0), j = 1,2,— ,n Step 5: Calculate the distance of each alternative from A+ and A" using the vertex method. d+= Tlrj=id(vij,v+)^i d" = Xr^idCVij’V-jvi Step 6: Calculate the closeness coefficient (CCt) for each alternative and rank the alternatives in decreasing order of the closeness coefficient (from best to worst). CCt = d-d-+d+ Vi As CCt approaches 1, alternative At is closer to A+ and farther from A .
3. Methodology The methodology described in the given research involves the application of two distinct decision-making methods, F-AHP with Chang's extent analysis approach and F-TOPSIS. The research focuses on enhancing the selection and ranking process for alternative the position of mobile software developer candidates. The methodology is explained below: a. Identification of Selection Criteria for Mobile Software Developer Candidates: In this phase, the focus is on determining the essential criteria that will be used in the selection process of mobile software developer candidates. Relevant and critical attributes are identified, considering factors such as technical skills, experience, communication abilities, and other key competencies. The goal is to establish a comprehensive set of criteria that will be used to evaluate and compare potential candidates for the position. b. Implementation of F-AHP with Chang's Extent Analysis Approach: This step involves two main components: • Data Collection from Stakeholders: Gather input and assessments from stakeholders, which may include team leaders, project managers, or other relevant individuals. This information is crucial for understanding the importance of each criterion in the selection process. • Application of F-AHP: Utilize the F-AHP method to assign weights to the identified criteria. This involves a systematic analysis of pairwise comparisons and the incorporation of fuzzy logic to handle uncertainties in decision-making. Additionally, Chang's extent analysis approach is applied to refine the comparison values, providing a more accurate representation of the criteria weights. c. Integration of F-AHP Results into F-TOPSIS: After determining the criterion weights through F-AHP, the next step is to integrate these results into the F-TOPSIS method: • Retrieval of Criterion Weights: Collect the weights assigned to each criterion during the F-AHP process. • Application of F-TOPSIS: Utilize F-TOPSIS to rank mobile software developer candidates based on the previously obtained criterion weights. This involves calculating the closeness of each candidate to the ideal solution. • Preparation of Alternative Data: As part of the F-TOPSIS method, alternative data representing the candidates is prepared. This data includes the performance-related information of each candidate based on the established criteria. d. Identification of Alternative Mobile Software Developer Candidates: In this step, the emphasis is on specifying and gathering information about the potential candidates for the mobile software developer position: • Candidate Specification: Define the list of mobile software developer candidates who will undergo evaluation. • Data Gathering: Collect performance-related data for each candidate, focusing on their qualifications, experience, and capabilities related to the identified criteria. e. Implementation of F-TOPSIS for Ranking Mobile Software Developer Candidates: The final stage involves the application of the F-TOPSIS method to rank the identified candidates based on their closeness to the ideal solution: • F-TOPSIS Calculation: Employ F-TOPSIS to calculate the closeness value for each candidate, considering their performance against the established criteria. • Candidate Ranking: Rank the mobile software developer candidates based on the F-TOPSIS scores generated, providing a comprehensive assessment that incorporates both the criteria weights from F-AHP and the performance data from stakeholders. These steps collectively form a systematic approach to enhancing the selection process for mobile software developer candidates through the integration of F-AHP and F-TOPSIS methodologies. This research was conducted at a software development company located in Bandung, Indonesia. The company is in a phase of growth, with more than 50 employees and over 5 years of operational experience. The focus of the study was on analyzing the recruitment process within the company, particularly in the context of selecting employees for the position of mobile software developer. In this process, three experts were involved, namely the Software Development Manager, HRD Manager, and Senior Software Engineer, collectively referred to as decision-makers (coded as DM-1, DM-2, and DM-3). There were ten potential candidates (m = 10) considered for the role of a mobile software developer. The responsibilities of a mobile software developer at the software development company include designing, developing, testing, and maintaining software to meet the company's or clients' needs. They work to create efficient, reliable, and innovative software solutions, actively participating in problem-solving and software product improvement. In addition, they collaborate with cross-disciplinary teams, ensuring that the software product complies with security and quality standards and stays abreast of the latest technological developments. The relevant criteria and sub-criteria are determined based on policy documents and assessed using a form designed in collaboration with decision-makers. Then, forms utilized in the employee recruitment process and documents containing job applicant profiles serve as sources of information. Further details are outlined in Table 2. Table 2. Criteria and Sub-Criteria for Mobile Software Developer Qualifications Criteria Sub-Criteria Descriptions General Qualifications (GQ) a. Education (GQ1) b. Work Experience (GQ2) c. Language Proficiency (GQ3) d. Analytical Skills (GQ4) • Minimum Bachelor's degree (BSc) in Computer Science, Software Engineering, or a related field. • Additional certifications or relevant courses in mobile software development are a plus. • Minimum 2 years of experience as a Mobile Software Developer. • Experience in developing mobile applications for both Android and iOS platforms. • Good communication skills in English (both verbal and written). • Ability to work in a multicultural or multinational team is an advantage. • Strong analytical skills to understand user needs and design effective solutions. Technical Qualifications (TQ) a. Programming Language Mastery (TQ1) b. Software Architecture (TQ2) c. API Development (TQ3) d. Application Security (TQ4) • Proficiency in programming languages such as Java (for Android) or Swift (for iOS). • Experience with cross-platform development frameworks like Flutter or React Native. • In-depth knowledge of mobile software architecture. • Experience in designing and implementing clean and scalable architectures. • Experience in API integration and development. • Knowledge of RESTful API concepts. • Understanding of software security practices and implementation of mobile application security standards. Soft-Skill Qualifications (SQ) a. Communication Skills (SQ1) b. Adaptability (SQ2) c. Teamwork (SQ3) d. Initiative and Creativity (SQ4) • Excellent communication skills, both within the team and with stakeholders. • Effective presentation skills. • Flexibility and adaptability to changing project requirements. • Ability to work in a dynamic environment. • Strong teamwork skills and ability to collaborate effectively. • Ability to give and receive constructive feedback. • Ability to take initiative and complete tasks without constant supervision. • Creativity in finding innovative solutions. Once the relevant criteria and sub-criteria are established, the F-AHP method is employed to determine the weights for these criteria and sub-criteria. Subsequently, the F-TOPSIS method is utilized to rank potential employee alternatives for the mobile software developer role using the predetermined weights. Within the framework of the F-AHP method, decision-makers engage in pairwise comparisons for all criteria and sub-criteria. This assessment employs linguistic terms and membership functions corresponding to triangular fuzzy numbers (TFN), as detailed in Table 3. Table 3. Fuzzy assessment scores used in pairwise comparisons within F-AHP Linguistic terms Membership function Very strong (VS) (2, 5/2, 3) Extremely strong (ES) (3/2, 2, 5/2) Quite strong (QS) (1, 3/2, 2) Moderately strong (MS) (1, 1, 3/2) Same (S) (1, 1, 1) Moderately weak (MW) (2/3, 1, 1) Quite weak (QW) (1/2, 2/3, 1) Very weak (VW) (2/5, 1/2, 2/3) Extremely weak (EW) (1/3, 2/5, 1/2) After finalizing the identification of criteria and sub-criteria, the subsequent stage includes the development of a matrix for pairwise comparisons to assess the significance or connections among elements within the hierarchy. Experts or decision-makers conduct this evaluation by assigning relative values to each pair of elements. Table 4 presents the pairwise comparisons for the primary criteria as assessed by three decision-makers. Table 4. Pairwise comparison for the primary criteria GQ TQ SQ GQ (S, S, S) (VW, QW, VW) (MS, S, MS) TQ (ES, QS, ES) (S, S, S) (QS, QS, MS) SQ (QW, S, MW) (MW, QW, MW) (S, S, S) The pairwise comparison results for the general qualification sub-criteria are presented in Table 5. A similar approach is also applied to the other sub-criteria. Table 5. Pairwise comparison for the primary criteria General Qualification (GQ) GQ1 GQ2 GQ3 GQ4 GQ1 (S, S, S) (QW, QW, QW) (MS, MS, MS) (MW, MS, MW) GQ2 (QS, QS, QS) (S, S, S) (MS, MS, QS) (MS, MS, MS) GQ3 (MW, MW, MW) (MW, MW, QW) (S, S, S) (MW, S, MW) GQ4 (MS, MW, MS) (MW, MW, MW) (MS, S, MS) (S, S, S) Subsequently, all the results of pairwise comparisons are transformed based on the values of TFN as outlined in Table 3. The conversion results for the main criteria are presented in Table 6. Meanwhile, the conversion for all subcriteria is conducted using a similar method as for the main criteria. The transformation to TFN serves the purpose of incorporating uncertainty into decision analysis, enabling decision-makers to manage uncertainties and ambiguities inherent in the utilized data or information. Table 6. Pairwise comparison for the main criteria GQ TQ SQ DM-1 DM-2 DM-3 DM-1 DM-2 DM-3 DM-1 DM-2 DM-3 GQ (1, 1, 1) (1, 1, 1) (1, 1, 1) (2/5, 1/2, 2/3) (1/2, 2/3, 1) (2/5, 1/2, 2/3) (1, 1, 3/2) (1, 1, 1) (1, 1, 3/2) TQ (3/2, 2, 5/2) (1, 3/2, 2) (3/2, 2, 5/2) (1, 1, 1) (1, 1, 1) (1, 1, 1) (1, 3/2, 2) (1, 3/2, 2) (1, 1, 3/2) SQ (1/2, 2/3, 1) (1, 1, 1) (2/3, 1, 1) (2/3, 1, 1) (1/2, 2/3, 1) (2/3, 1, 1) (1, 1, 1) (1, 1, 1) (1, 1, 1) The next step involves determining the average values of elements in the pairwise comparison matrix for each criterion by processing the element values using Equation (8). For example, in the GQ row, the calculation results can be seen below. GQ: г = (1 +1 +1)3 = i,ooo m = (1 + 1 + 1)3 = 1,000 u = (1 + 1 + 1)3 = 1,000 TQ: г = ((2/5) + (1/2) + 1)3 = 0,433 m = ((1/2) + (2/3) + 1)3 = 0,556 u = ((2/3) + 1 + 1)3 = 0,778 SQ: г = (1 + 1 + 1)3 = 1,000 m = (1 + 1 + 1)3=1,000 u = ((3/2) + 1 + (3/2))3 = 1,333 The calculation results for the main criteria are presented in Table 7. The calculations for the sub-criteria of general qualifications can be found in Table 8. For other sub-criteria, a similar approach is applied as for the main criteria and the sub-criteria of general qualifications. Table 7. Aggregated fuzzy evaluation matrix of the main criteria GQ TQ SQ l m u l m u l m u GQ 1,000 1,000 1,000 0,433 0,556 0,778 1,000 1,000 1,333 TQ 1,333 1,833 2,333 1,000 1,000 1,000 1,000 1,333 1,833 SQ 0,722 0,889 1,000 0,611 0,889 1,000 1,000 1,000 1,000 Table 8. Aggregated fuzzy evaluation matrix of the sub criteria General Qualification (GQ) GQ1 GQ2 GQ3 GQ4 l m u l m u l m u l m u GQ1 1,000 1,000 1,000 0,500 0,667 1,000 1,000 1,000 1,500 0,778 1,000 1,167 GQ2 1,000 1,500 2,000 1,000 1,000 1,000 1,000 1,167 1,667 1,000 1,000 1,500 GQ3 0,667 1,000 1,000 0,611 0,889 1,000 1,000 1,000 1,000 0,778 1,000 1,000 GQ4 0,889 1,000 1,333 0,667 1,000 1,000 1,000 1,000 1,333 1,000 1,000 1,000 After obtaining the average pairwise comparison values, the next step is defuzzification according to Equation (9). For example, in the GQ row, the calculation results can be seen below. GQ = 1,000 + (4 x 1,000) + 1,000 =1,000 TQ = 0,433 + (4 x 0,556) + 0,778 =0,572 SQ = 1,000 + (4 x 1,000) + 1,333 =1,056 The results are then adjusted into a normalized form by dividing each element of the defuzzification matrix by its column sum. Table 9 shows the defuzzification results for the main criteria, while Table 10 contains the normalized results from this process. The calculation for sub-criteria follows a similar method as for the main criteria. Table 9. Defuzzification matrix of the main criteria GQ TQ SQ GQ 1,000 0,572 1,056 TQ 1,833 1,000 1,361 SQ 0,880 0,861 1,000 Table 10. Defuzzification matrix of the main criteria GQ TQ SQ GQ 0,269 0,235 0,309 TQ 0,494 0,411 0,398 SQ 0,237 0,354 0,293 Using the matrix of pairwise comparison results, calculations are performed for the fuzzy synthetic values (S,), weights from Chang's extent analysis (W/), and the normalized weights (IV,). Table 11 illustrates the calculation results for the main criteria. Meanwhile, calculations for sub-criteria are conducted with a similar approach as applied to the main criteria. This approach ensures consistency in the evaluation method between the main criteria and sub-criteria, facilitating a comprehensive interpretation of the results. By employing this approach, the evaluation of both levels of criteria can be conducted more systematically and transparently. The final results of this calculation provide a clear overview of the contribution of each criterion and sub-criterion to the overall evaluation. Table 11. Fuzzy synthetic extent values (St), weights (IV/) and normalized weights (W;) of the main criteria •Si wt' = d' (C) W; = d(Ct)T l m u GQ 0,216 0,269 0,384 0,343 0,204 TQ 0,296 0,439 0,638 1,000 0,595 SQ 0,207 0,292 0,370 0,338 0,201 After the calculation of weights (Wt) is completed, the entire matrix of fuzzy pairwise comparison results has undergone both defuzzification and normalization. From the results, AW = AmaxW, where Amax is calculated for each matrix. By applying Equation (21) and Equation (22), the consistency ratio (CR) is calculated. Considering all CR values are less than 0.1 (CR< 0.10) as indicated in Table 12, this comparison is considered acceptable. Table 12. Consistency ratio (CR) Main Criteria Sub Criteria GQ TQ SQ Ordo 3 x 3 4 x 4 4 x 4 4 x 4 CI 0,04 0,02 0,02 0,03 RI 0,58 0,90 0,90 0,90 CR<0.1 0,06 0,02 0,02 0,03 The final weights for all sub-criteria are obtained by multiplying the weight values for the main criteria with the weight values for the sub-criteria in each group of main criteria. This process illustrates the relative contribution of each sub-criterion to the main criteria in each group. The results can be seen in Table 13, which will be used in the F-TOPSIS calculation. In the F-TOPSIS stage, decision-makers evaluate each alternative (mobile software developer candidates) based on individual sub-criteria using linguistic concepts outlined in Table 14. Evaluation of 10 alternatives (10 mobile software developer candidates, hereafter referred to as CK-1 to CK-10) considering 12 sub-criteria by 3 decision-makers (DM-1, DM-2, and DM-3) utilizing linguistic terms in Table 14. Table 15 shows the evaluation results for general qualifications. For other qualifications, the process is carried out similarly to the evaluation of general qualifications. These linguistic terms are then converted into the corresponding Triangular Fuzzy Numbers (TFN) with membership values in Table 14. The fuzzy decision matrix for the main criteria can be seen in Table 16. All sub-criteria presented in this context are assumed to be benefit criteria (B). Further, using Equation (23) and Equation (24), the formation of the normalized fuzzy decision matrix, the fuzzily weighted normalized decision matrix is created as shown in Table 17 for the main criteria. Table 13. The Final Result of Weight Values in F-AHP Main Criteria Wt Sub-Criteria Wy W GQ 0,204 GQ1 0,231 0,047 GQ2 0,339 0,069 GQ3 0,215 0,044 GQ4 0,215 0,044 TQ 0,595 TQ1 0,586 0,349 TQ2 0,230 0,137 TQ3 0,092 0,055 TQ4 0,092 0,055 SQ 0,201 SQ1 0,271 0,055 SQ2 0,247 0,050 SQ3 0,241 0,049 SQ4 0,241 0,049 Table 14. Evaluation of Alternatives for General Qualification by Three Decision-Makers. Linguistic term Code Membership function Very Poor SK (0, 0, 1) Poor K (0, 1, 3) Quite Poor CK (1, 3, 5) Moderate S (3, 5, 7) Fairly Good CB (5, 7, 9) Good B (7, 9, 10) Very Good SB (9, 10, 10) Table 15. Fuzzy Evaluation Values for Each Alternative in F-TOPSIS GQ1 GQ2 GQ3 GQ4 DM-1 DM-2 DM-3 DM-1 DM-2 DM-3 DM-1 DM-2 DM-3 DM-1 DM-2 DM-3 CK-1 S SB B S CK B S SB SB CB SB B CK-2 S CB B CK SB B CK CK S CB CB CK CK-3 CK S SB CB B CB SB CK S CK CB S CK-4 CK S SB CB SB CK SB CK SB SB B S CK-5 B S CK CB B CB B CK SB B CK B CK-6 CB CB CK B CB B B SB SB S SB CK CK-7 B SB S S CB S S B SB B S B CK-8 B B CB CK CB SB SB S B CB S CB CK-9 CB SB CB S S SB S B B B SB B CK-10 CB S CK B B CB CK B CB B S B Table 16. Fuzzy Decision Matrix (D) for Main Criteria GQ1 GQ2 GQ3 GQ4 DM-1 DM-2 DM-3 DM-1 DM-2 DM-3 DM-1 DM-2 DM-3 DM-1 DM-2 DM-3 l m u l m u l m u l m u l m u l m u l m u l m u l m u l m u l m u l m u CK-1 3 5 7 9 10 10 7 9 10 3 5 7 1 3 5 7 9 10 3 5 7 9 10 10 9 10 10 5 7 9 9 10 10 7 9 10 CK-2 3 5 7 5 7 9 7 9 10 1 3 5 9 10 10 7 9 10 1 3 5 1 3 5 3 5 7 5 7 9 5 7 9 1 3 5 CK-3 1 3 5 3 5 7 9 10 10 5 7 9 7 9 10 5 7 9 9 10 10 1 3 5 3 5 7 1 3 5 5 7 9 3 5 7 CK-4 1 3 5 3 5 7 9 10 10 5 7 9 9 10 10 1 3 5 9 10 10 1 3 5 9 10 10 9 10 10 7 9 10 3 5 7 CK-5 7 9 10 3 5 7 1 3 5 5 7 9 7 9 10 5 7 9 7 9 10 1 3 5 9 10 10 7 9 10 1 3 5 7 9 10 CK-6 5 7 9 5 7 9 1 3 5 7 9 10 5 7 9 7 9 10 7 9 10 9 10 10 9 10 10 3 5 7 9 10 10 1 3 5 CK-7 7 9 10 9 10 10 3 5 7 3 5 7 5 7 9 3 5 7 3 5 7 7 9 10 9 10 10 7 9 10 3 5 7 7 9 10 CK-8 7 9 10 7 9 10 5 7 9 1 3 5 5 7 9 9 10 10 9 10 10 3 5 7 7 9 10 5 7 9 3 5 7 5 7 9 CK-9 5 7 9 9 10 10 5 7 9 3 5 7 3 5 7 9 10 10 3 5 7 7 9 10 7 9 10 7 9 10 9 10 10 7 9 10 CK-10 5 7 9 3 5 7 1 3 5 7 9 10 7 9 10 5 7 9 1 3 5 7 9 10 5 7 9 7 9 10 3 5 7 7 9 10 Table 17. Fuzzy weighted normalized decision matrix (V) GQ1 GQ2 GQ3 GQ4 l m u l m u l m u l m u CK-1 0,300 0,800 1,000 0,100 0,567 1,000 0,300 0,833 1,000 0,500 0,867 1,000 CK-2 0,300 0,700 1,000 0,100 0,733 1,000 0,100 0,367 0,700 0,100 0,567 0,900 CK-3 0,100 0,600 1,000 0,500 0,767 1,000 0,100 0,600 1,000 0,100 0,500 0,900 CK-4 0,100 0,600 1,000 0,100 0,667 1,000 0,100 0,767 1,000 0,300 0,800 1,000 CK-5 0,100 0,567 1,000 0,500 0,767 1,000 0,100 0,733 1,000 0,100 0,700 1,000 CK-6 0,100 0,567 0,900 0,500 0,833 1,000 0,700 0,967 1,000 0,100 0,600 1,000 CK-7 0,300 0,800 1,000 0,300 0,567 0,900 0,300 0,800 1,000 0,300 0,767 1,000 CK-8 0,500 0,833 1,000 0,100 0,667 1,000 0,300 0,800 1,000 0,300 0,633 0,900 CK-9 0,500 0,800 1,000 0,300 0,667 1,000 0,300 0,767 1,000 0,700 0,933 1,000 CK-10 0,100 0,500 0,900 0,500 0,833 1,000 0,100 0,633 1,000 0,300 0,767 1,000 The next step involves calculations to obtain the values for the positive ideal solution and negative ideal solution using Equation (25). Afterward, calculate the distance of each alternative to the positive ideal solution and negative ideal solution using Equation (26). Taking into account the distance from the fuzzy positive ideal solution (d+), the distance from the fuzzy negative ideal solution (d-), the closeness coefficient (CQ) is calculated using Equation (27). The results of these calculations can be seen in Table 18. Table 18. The results of F-AHP and F-TOPSIS d+ d- CC Rank CK-1 0,282 0,172 0,378 6 CK-2 0,304 0,129 0,298 8 CK-3 0,268 0,188 0,412 5 CK-4 0,343 0,096 0,218 10 CK-5 0,348 0,104 0,231 9 CK-6 0,255 0,187 0,423 4 CK-7 0,171 0,262 0,605 1 CK-8 0,303 0,138 0,313 7 CK-9 0,232 0,233 0,501 2 CK-10 0,238 0,210 0,468 3 Based on Table 18, CK-7 has the highest closeness coefficient (CQ), thus obtaining the rank of 1, while CK-4 has the lowest CQ value and is ranked 10. These rankings can serve as the basis for decision-making or selecting the best alternative. Expanding the discussion on the implications, it is crucial to explore the broader impact on HR practices and IT industry standards. The integration of F-AHP and F-TOPSIS methods in employee selection processes not only enhances decision-making accuracy but also sets a precedent for innovation in human resource management (HRM) methodologies within the technology sector. By adopting advanced decision-making frameworks rooted in fuzzy logic, organizations can streamline their recruitment processes, ensuring the acquisition of top-tier talent that aligns with evolving industry demands. Furthermore, the application of fuzzy logic techniques in employee selection extends beyond individual companies, potentially influencing industry-wide standards and best practices. As organizations witness the efficacy of these integrated methodologies, there exists an opportunity for the establishment of standardized frameworks that optimize HR processes across the IT landscape. This could catalyze a paradigm shift in how talent is identified, evaluated, and onboarded within the technology sector, fostering greater efficiency and competitiveness in the global marketplace. Moreover, the findings of this study underscore the importance of embracing technological advancements in HRM practices to remain agile and responsive to evolving business dynamics. In an era characterized by digital transformation and rapid innovation, organizations that leverage sophisticated decision-making tools and methodologies are better equipped to navigate the complexities of talent acquisition and retention. By integrating fuzzy logic-based approaches into HRM frameworks, companies can adapt to changing market conditions, mitigate risks, and capitalize on emerging opportunities in the highly competitive IT ecosystem. In conclusion, the adoption of integrated fuzzy logic methodologies in employee selection processes not only optimizes HR practices within individual organizations but also contributes to the evolution of industry-wide standards and practices. By embracing innovation and leveraging advanced decision-making frameworks, companies can unlock new avenues for talent acquisition, drive operational excellence, and enhance their competitive advantage in the dynamic landscape of the technology industry.
5. Conclusion In the context of optimizing the selection of mobile software developer candidates, the Fuzzy Analytic Hierarchy Process (F-AHP) and Fuzzy Technique for Order of Preference by Similarity to Ideal Solution (F-TOPSIS) methods are employed to evaluate and choose the most optimal employee alternatives. The final results showcase the evaluation outcomes for ten candidate employees (CK-1 to CK-10) based on F-TOPSIS calculations, incorporating information from F-AHP. The closeness coefficient (CC;) values reflect the extent to which each candidate approaches the positive ideal solution and avoids the negative ideal solution. CK-7 secures the highest rank with the highest CC[ value, while CK-4 obtains the lowest rank. This indicates that CK-7 performs better than the others, while CK-4 exhibits a comparatively lower performance. These results can aid decision-making related to the selection of mobile software developer candidates. Candidates who receive high rankings, such as CK-7, can be considered more optimal choices in the selection process. This method enables the integration of fuzzy or uncertain decision aspects, providing a more comprehensive and accurate understanding in choosing candidates that align with the company's needs in the ever-changing environment of the information technology industry. For future research, it is suggested to compare the results of this study with other fuzzy MCDM methods like fuzzy PROMETHEE, VIKOR, and ELECTRE. Additionally, exploring correlations between criteria can be conducted using correlated fuzzy AHP, studying network relationships with fuzzy analytic network process (ANP), and integrating these methods with fuzzy TOPSIS for comprehensive MCDM ranking problem analyses.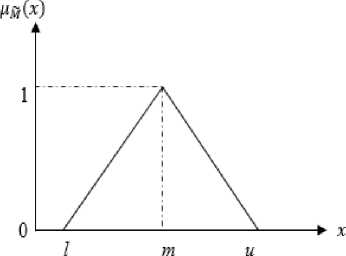
Список литературы Enhancing Mobile Software Developer Selection through Integrated F-AHP and F-TOPSIS Methods
- L. A. Zadeh, “Fuzzy sets,” Information and Control, vol. 8, no. 3, pp. 338–353, 1965, doi: 10.1016/S0019-9958(65)90241-X.
- L. A. Zadeh, “Fuzzy Logic, Neural Networks, and Soft Computing,” Communications of the ACM, vol. 37, no. 3, 1994, doi: 10.1145/175247.175255.
- Y. Wang et al., “Abstract intelligence: Embodying and enabling cognitive systems by mathematical engineering,” International Journal of Cognitive Informatics and Natural Intelligence, vol. 11, no. 1, 2017, doi: 10.4018/IJCINI.2017010101.
- R. Cheng, R. Zhu, Y. Tian, B. Kang, and J. Zhang, “A multi-criteria group decision-making method based on OWA aggregation operator and Z-numbers,” Soft Computing, vol. 27, no. 3, 2023, doi: 10.1007/s00500-022-07667-8.
- N. Quang Vinh, Q. H. Do, and L. M. Hien, “An integrated fuzzy AHP and fuzzy TOPSIS approach in the hotel industry,” International Journal of Advanced and Applied Sciences, vol. 9, no. 10, 2022, doi: 10.21833/ijaas.2022.10.017.
- D. S. Utomo, D. Cahyadi, I. F. Astuti, and G. M. Putra, “Selection of Promotional Media on Tourist Boats with Fuzzy AHP and Fuzzy TOPSIS,” International Journal of ADVANCED AND APPLIED SCIENCES, vol. 10, no. 5, 2023, doi: 10.21833/ijaas.2023.05.017.
- T. L. Satty, Group decision making and the AHP The analytic hierarchy process. 1989.
- T. L. Saaty, “Correction to: Some mathematical concepts of the analytic hierarchy process,” Behaviormetrika, vol. 48, no. 1, 2021, doi: 10.1007/s41237-020-00125-5.
- N. T. Pham et al., “Research on knowledge management models at universities using fuzzy analytic hierarchy process (FAHP),” Sustainability (Switzerland), vol. 13, no. 2, 2021, doi: 10.3390/su13020809.
- T. T. Hue et al., “Prioritization of Factors Impacting Lecturer Research Productivity Using an Improved Fuzzy Analytic Hierarchy Process Approach,” Sustainability (Switzerland), vol. 14, no. 10, 2022, doi: 10.3390/su14106134.
- S. Barbounaki and A. Sarantaki, “Construction and validation of a preterm birth risk assessment model using fuzzy analytic hierarchy process,” Bosnian Journal of Basic Medical Sciences, vol. 22, no. 2, 2022, doi: 10.17305/bjbms.2021.6431.
- M. Marzouk, N. Elshaboury, S. Azab, A. Megahed, and M. Metawie, “Assessment of COVID-19 impact on sustainable development goals indicators in Egypt using fuzzy analytic hierarchy process,” International Journal of Disaster Risk Reduction, vol. 82, 2022, doi: 10.1016/j.ijdrr.2022.103319.
- A. G. Abdullah, A. H. Setiorini, N. A. Dwitasari, D. L. Hakim, and M. Aziz, “Location suitability analysis for wind farm exploitation using fuzzy analytic hierarchy process,” Indonesian Journal of Science and Technology, vol. 6, no. 3, 2021, doi: 10.17509/ijost.v6i3.38957.
- F. Kutlu Gündoğdu, S. Duleba, S. Moslem, and S. Aydın, “Evaluating public transport service quality using picture fuzzy analytic hierarchy process and linear assignment model,” Applied Soft Computing, vol. 100, 2021, doi: 10.1016/j.asoc.2020.106920.
- M. Z. Djordjevic, A. Djordjevic, E. Klochkova, and M. Misic, “Application of Modern Digital Systems and Approaches to Business Process Management,” Sustainability (Switzerland), vol. 14, no. 3, 2022, doi: 10.3390/su14031697.
- A. Gupta, R. K. Singh, and S. Gupta, “Developing human resource for the digitization of logistics operations: readiness index framework,” International Journal of Manpower, vol. 43, no. 2, 2022, doi: 10.1108/IJM-03-2021-0175.
- K. Yoon and C.-L. Hwang, Multiple Attribute Decision Making. 2011. doi: 10.4135/9781412985161.
- R. Mitra, J. Das, and M. Kamruzzaman, “Application of TOPSIS method for flood susceptibility mapping using Excel and GIS,” MethodsX, vol. 11, 2023, doi: 10.1016/j.mex.2023.102263.
- H. M. Putri, “Identifikasi Pemenang Tender Pengadaan Barang Menggunakan Metode TOPSIS,” KESATRIA : Jurnal Penerapan Sistem Informasi (Komputer & Manajemen), vol. 4, no. 1, 2023.
- Y. Zhu, C. Chen, G. Zhang, Z. Lin, S. G. Meshram, and E. Alvandi, “Investigation of West Lake Ecotourism Capabilities Using SWOT and TOPSIS Decision-Making Methods,” Sustainability (Switzerland), vol. 15, no. 3, 2023, doi: 10.3390/su15032464.
- M. Marzouk, M. El-Maraghy, and M. Metawie, “Assessing retrofit strategies for mosque buildings using TOPSIS,” Energy Reports, vol. 9, 2023, doi: 10.1016/j.egyr.2022.12.073.
- S. Singh, V. Agrawal, K. K. Saxena, and K. A. Mohammed, “Optimization on Manufacturing Processes at Indian Industries Using TOPSIS,” Indian Journal of Engineering and Materials Sciences, vol. 30, no. 1, 2023, doi: 10.56042/ijems.v1i1.61931.
- S. Fanaei, A. Zareiyan, S. Shahraki, and A. Mirzaei, “Determining the key performance indicators of human resource management of military hospital managers; a TOPSIS study,” BMC Primary Care, vol. 24, no. 1, 2023, doi: 10.1186/s12875-023-02007-7.
- K. M. Doka, F. Ahmad, S. N. Wan Shamsuddin, W. S. Wan Awang, and N. Ghazali, “Integrated decision support system for human resource selection using TOPSIS based models,” Applied Mathematical Sciences, vol. 9, no. 129, 2015, doi: 10.12988/ams.2015.53288.
- A. I. Khan et al., “Integrating Blockchain Technology Into Healthcare Through an Intelligent Computing Technique,” Computers, Materials and Continua, vol. 70, no. 2, 2022, doi: 10.32604/cmc.2022.020342.
- A. Saxena and A. K. Yadav, “Evaluating the Appropriate Fuel-Based Bus Technology in Indian Context by Integrating Fuzzy AHP-Fuzzy TOPSIS,” European Transport - Trasporti Europei, no. 92, 2023, doi: 10.48295/ET.2023.92.6.
- H. Alhassan, N. Peleato, and R. Sadiq, “Mercury Risk Reduction in Artisanal and Small-Scale Gold Mining: A Fuzzy AHP-Fuzzy TOPSIS Hybrid Analysis,” Resources Policy, vol. 83, 2023, doi: 10.1016/j.resourpol.2023.103744.
- N. Mehdiyev, “Selection Core Banking System by Using Fuzzy AHP and Fuzzy TOPSIS Hybrid Method,” in Lecture Notes in Networks and Systems, 2023. doi: 10.1007/978-3-031-25252-5_67.
- V. Kukreja, “Hybrid Fuzzy AHP–TOPSIS Approach to Prioritizing Solutions for Inverse Reinforcement Learning,” Complex and Intelligent Systems, vol. 9, no. 1, 2023, doi: 10.1007/s40747-022-00807-5.
- M. Sequeira, A. Adlemo, and P. Hilletofth, “A Hybrid Fuzzy-AHP-TOPSIS Model for Evaluation of Manufacturing Relocation Decisions,” Operations Management Research, vol. 16, no. 1, 2023, doi: 10.1007/s12063-022-00284-6.
- N. L. Rane and S. P. Choudhary, “Fuzzy AHP and Fuzzy TOPSIS as an Effective and Powerful Multi-Criteria Decision-Making (MCDM) Method for Subjective Judgements in Selection Process,” International Research Journal of Modernization in Engineering Technology and Science, 2023, doi: 10.56726/irjmets36629.
- S. Swethaa and A. Felix, “An Intuitionistic Dense Fuzzy AHP-TOPSIS Method for Military Robot Selection,” Journal of Intelligent and Fuzzy Systems, vol. 44, no. 4, 2023, doi: 10.3233/JIFS-223622.
- P. Li, S. A. Edalatpanah, A. Sorourkhah, S. Yaman, and N. Kausar, “An Integrated Fuzzy Structured Methodology for Performance Evaluation of High Schools in a Group Decision-Making Problem,” Systems, vol. 11, no. 3, 2023, doi: 10.3390/systems11030159.
- M. H. Luc, Q. V. Nguyen, Q. H. Do, and T. Van Trang, “Evaluation of an Apartment Selection Model by Integrating Fuzzy AHP and Fuzzy TOPSIS,” International Journal of Fuzzy System Applications, vol. 11, no. 1, 2022, doi: 10.4018/IJFSA.313964.
- N. Q. Trung and N. Van Thanh, “Evaluation of Digital Marketing Technologies with Fuzzy Linguistic MCDM Methods,” Axioms, vol. 11, no. 5, 2022, doi: 10.3390/axioms11050230.
- R. Ulewicz, D. Siwiec, A. Pacana, M. Tutak, and J. Brodny, “Multi-Criteria Method for The Selection of Renewable Energy Sources in the Polish Industrial Sector,” Energies, vol. 14, no. 9, 2021, doi: 10.3390/en14092386.
- S. H. Almotiri, “Integrated Fuzzy Based Computational Mechanism for the Selection of Effective Malicious Traffic Detection Approach,” IEEE Access, vol. 9, 2021, doi: 10.1109/ACCESS.2021.3050420.
- N. M. T. Nong and D. S. Ha, “Application of MCDM methods to Qualified Personnel Selection in Distribution Science: Case of Logistics Companies,” Journal of Distribution Science, vol. 19, no. 8, 2021, doi: 10.15722/jds.19.8.202108.25.
- Y. D. Uslu, E. Yılmaz, and P. Yiğit, “Developing Qualified Personnel Selection Strategies Using MCDM Approach: A University Hospital Practice,” in Strategic Outlook in Business and Finance Innovation: Multidimensional Policies for Emerging Economies, 2021. doi: 10.1108/978-1-80043-444-820211018.
- M. M. I. Rahi, A. K. M. A. Ullah, and D. M. G. R. Alam, “A Decision Support System (DSS) for Interview-Based Personnel Selection Using Fuzzy TOPSIS Method,” in Lecture Notes in Networks and Systems, 2022. doi: 10.1007/978-981-19-2445-3_45.
- A. Akmaludin, E. G. Sihombing, R. Rinawati, F. Handayanna, L. Sari Dewi, and E. Arisawati, “Generation 4.0 of the Programmer Selection Decision Support System: MCDM-AHP and ELECTRE-Elimination Recommendations,” International Journal of Advances in Applied Sciences, vol. 12, no. 1, 2023, doi: 10.11591/ijaas.v12.i1.pp48-59.
- I. Ikah and R. Fitriani, “Penentuan Prioritas Kriteria Pada Proses Rekrutmen dan Seleksi Karyawan Menggunakan Metode Analytic Hierarchy Process di PT Citatah Tbk,” Jurnal Serambi Engineering, vol. 7, no. 2, 2022, doi: 10.32672/jse.v7i2.3957.
- X. He, Z. Xie, and C. H. Wang, “Selection of New Employees in Environmental Technology Company by MCDM,” Journal of Environmental Protection and Ecology, vol. 22, no. 3, 2021.
- T. Danişan, E. Özcan, and T. Eren, “Personnel Selection with Multi-Criteria Decision Making Methods in the Ready-to-Wear Sector,” Tehnicki Vjesnik, vol. 29, no. 4, 2022, doi: 10.17559/TV-20210816220137.
- Y. Ozdemir and K. G. Nalbant, “Personnel Selection for Promotion using an Integrated Consistent Fuzzy Preference Relations - Fuzzy Analytic Hierarchy Process Methodology: A Real Case Study,” Asian Journal of Interdisciplinary Research, 2020, doi: 10.34256/ajir20117.
- A. Raj Mishra, G. Sisodia, K. Raj Pardasani, and K. Sharma, “Multi-Criteria IT Personnel Selection on Intuitionistic Fuzzy Information Measures and ARAS Methodology,” Iranian Journal of Fuzzy Systems, vol. 17, no. 4, 2020, doi: 10.22111/ijfs.2020.5406.
- T. Kaya and C. Kahraman, “Multicriteria Decision Making in Energy Planning Using a Modified Fuzzy TOPSIS Methodology,” Expert Systems with Applications, vol. 38, no. 6, 2011, doi: 10.1016/j.eswa.2010.11.081.
- M. Sequeira, A. Adlemo, and P. Hilletofth, “A Hybrid Fuzzy-AHP-TOPSIS Model for Evaluation of Manufacturing Relocation Decisions,” Operations Management Research, vol. 16, no. 1, 2023, doi: 10.1007/s12063-022-00284-6.
- D. Y. Chang, “Applications of The Extent Analysis Method on Fuzzy AHP,” European Journal of Operational Research, vol. 95, no. 3, 1996, doi: 10.1016/0377-2217(95)00300-2.
- C. T. Chen, “Extensions of the TOPSIS for group decision-making under fuzzy environment,” Fuzzy Sets and Systems, vol. 114, no. 1, 2000, doi: 10.1016/S0165-0114(97)00377-1.


