Enhancing the Security in Cryptosystems Based on Magic Rectangle

Published Online April 2017 in MECS

As the progress of modern information technology is rapid, security is an important issue in many applications serving the domains such as e-commerce, internet access, etc. To protect the transmitted data from the eavesdropper, the message should be disguised before it is being transmitted through an insecure transmission channel and it is achieved by cryptosystem. It provides many security services like authentication, integrity, confidentiality and non-repudiation. A cryptographic system [1] consists of a plaintext message space M, a ciphertext message space C, an encryption key space K, and the decryption key space K´, an efficient key generation algorithm G : N ^ KxK, an efficient encryption algorithm E: MxK ^ C and an efficient decryption algorithm D: CxK- ^ M. For k eK, and m eM, we denote by C= Ek (m) and m = Dkd (C). There are two major classes of cryptosystems viz., private-key and public-key cryptosystems. In a private-key cryptosystem both encryption and decryption uses the same key i.e. kd = ke. In a public-key cryptosystems, encryption and decryption keys are different: for every ke eK , and kdfke.

It is noted that public-key algorithms are divided into three types viz., based on integer factorization, discrete logarithm and sum of subset problems. Integer factorization is a trapdoor function because based on p and q , n is computed easily but for given n , finding p and q is very difficult. Moreover the security of integer factorization based cryptosystem depends on the modulus n when n is very large. This is possible if the two primes p and q chosen are sufficiently large. It is noted that to enhance the security, an encoding scheme has been proposed for a character to be encrypted which is highly unpredictable. Though RSA algorithm is based on integer factorization it is not semantically secure or secure against chosen cipher text attacks even if all parameters p, q and encryption key (e, d) are chosen in such a way that it is infeasible to compute the secret key from the public key (n, e), choosing p, q are very large etc. Even if the above said parameters are taken carefully, none of the computational problems are fully secured enough [5].Because to encrypt the plaintext characters, their ASCII values are taken and if a character occurs in several places in a plaintext there is a possibility of same the cipher text is produced.

To overcome the problem, this paper attempts to develop a model with Magic Rectangle of order m×n denoted as MRm×n and each magic rectangle (MR) is considered as almost equal to one ASCII table. Thus, instead of taking ASCII values for the characters to encrypt, preferably different numerals representing the position of ASCII values are taken from MR and encryption is performed using RSA and ElGamal cryptosystems. Further, slow speed cryptosystems cause customer dissatisfaction. To avoid this, parallelism is done in performing cryptographic operations like encryption and decryption. A simulated environment has been set up in performing the said operations. For that Maui scheduler with back-filling philosophy is used in performing parallelism.

The rest of the paper is organized as follows. The various works related to construction of MR and their usage in cryptosystems is shown in section 2. Section 3 describes the proposed methodology for constructing the MR with an example. The usage of MR in performing encryption/decryption operation using public key cryptosystems are discussed in section 4. The experimental results are discussed in section 5. Finally, section 6 ends with conclusion.

• II.    Related Work

Michael Springfield, Wayne Goddard [2] have showed all possible MRs with arithmetic constraints. Enumerated the 4×4 domino magic squares in which rotations and reflections are considered. In [3], Chand K. Midha, et.al. have provided a simple and systematic method for constructing any m by m + 2 MR for m odd and also designed an algorithm. Praveen Kumar, et.al. [4] have implemented a magic square which attempts to augment the efficiency by providing add-on security to the cryptosystem. Also, the security was enhanced due to its complexity in encryption because it deals with the magic square.

In [6], M. Kiran Kumar and et.al. have proposed a safe mechanism of data transmission to tackle the security problem of information which is transmitted through Internet. Also, a new technique on matrix scrambling which is based on random function, shifting and reversing techniques of circular queue was proposed. They performed statistical analysis, sequence random analysis and sensitivity analysis to plaintext and key. Israa N. Alkallak [7] have solved Sudoku problem efficiently by an algorithm and also concluded by proposed heuristic algorithm from magic square of order S 3. And the author showed easy implementation to solve problem without manual method. Also, the author proved that the proposed algorithm was efficient algorithm to find a solution that yields near-optimal results very quickly.

Prashant Vasant Divasethe and et.al. [8] have proposed alternative techniques like graphical passwords and biometrics. A new technology for encryption and decryption that is MRGA was presented. In [9], Shikha Mathur, Deepika, Gupta have presented a modified approach of RSA which includes exponential form of RSA with four prime numbers and multiple (i.e. two) public keys with k-nearest neighbour algorithm. Nithiya Devi.G and et.al. [10], have proposed a strong algorithm for data security by combining new modified MR and iterative fisher Yates shuffle algorithm. The repetition of character in data was overcome through NMMR and complexity of the data was increased by introducing IFYS the shuffle algorithm along with NMMR. And proved that the data is hard to retrieve without the knowledge of magic pattern and shuffling order.

In [11], Omar A. Dawood and et.al., have developed a new method for constructing magic cube by using the folded magic square technique. The proposed method considered a new step towards the magic cube construction that applied a good insight and provided an easy generalized technique. The method generalized the design of magic cube with N order regardless the type of magic square whether odd order, singly even order or doubly even order. J. P. De Los Reyes and et.al. [12], provided a new systematic method for constructing any even MR. The method proposed was extremely simple as it allows one to arrive at the MRs by simply carrying out some matrix operations and the MRs of lower orders are embedded in a MR of higher order.

In [13], Kunal Jain and et. al. suggested a different kind of cryptosystem, a cryptosystem without any key. The combination of MR Generation Algorithm (MRGA) with Stenography was proposed by reducing the time and space to generate and store the different secure keys. These MRs were formed evenly on the basis of their seed number, row number, column number, start number, row sum and column sum. The author introduced another way of designing security without the use of key and overcoming the weakness of public key cryptosystems such as RSA, ElGamal etc.

Rinovia and et al. [14], studied some necessary conditions for the existence of D-distance magic graphs and magic labelling for cycles and D distance magic graphs was discussed. In [15], Dalibor Froneck has proved that MRs sets with a,b,c all odd and both a,b greater than one always exists. The author constructed the existence of MRS for all admissible triples of odd numbers were proved. John Lorch [16], have introduced a method using LP-linear transformation for producing a variety of pr×ps MRs. The author has introduced a linear– algebraic method which adds significance to known MRs with non-co prime dimensions. In [17], Feng Shun Chai has provided a systematic method for constructing p/q MRs where p and q >1 are any odd integers.

• III.    Proposed Methodology

The proposed methodology for any cryptosystems in enhancing the security is based on a novel method of constructing MR. It provides an additional layer of security because the ASCII encoding scheme is not taken for the character to be encrypted. But encoding of characters is performed based on MR. For that different MR mxn are formed where each MR is considered as ASCII table. To perform encoding based on MR, first find the ASCII value of the plaintext to be encrypted. Then the ASCII values are considered as positional value in the MR and locate the numeral from MR which is then used for encryption.

A. Construction of MRmxn

To construct the MR using the proposed methodology the number of rows, magic sum of order p and MR starting number denoted as m , MSS P and MRstart respectively are accepted as input. Then the number of columns of MR denoted as n is computed as n =m+2 and MSS p is treated as MR m×n csum . In the proposed methodology to compute MSS 2 from MSS p , divide and conquer strategy is used in this paper. For that different possible sub magic squares are generated denoted as subMSs and their corresponding sums are denoted as MSS are calculated using (1) and (2). The process is terminated when MSS₂ [5] is reached and MR_m×nrsum is computed based on MSS 2 where MSS 2 represents MSsum of order 2 using (3)

p k = p/2 ^k , k = 1,2,3,…, l-1            (1)

Tp

= Tn =

mxn—2

The sum ofall positive and negative numbers denoted as Sp and Sn respectively are calculated using (9) and (10) and their sum is zero as in (11)

Sp = T ^r i+

Sn = T ^r Г(10)

Further,

where l is an integer. It is found in such a way that when k=l-1 is substituted in (1), it will produce MS₂ .

MSSp k = MSSp/p k              (2)

MR_m×nrsum = Magic Sum or MR_m×n csum+MSS₂ (3)

After finding these, a generalized MR template denoted as MRT for MR is created. To obtain various MRTs further, the MRT can be permutated with the same MRstart and magic sum. Let MRT mxn denotes MRT of order mxn, where m and n are even numbers. To fill the values in MRT, first the range of numbers denoted as TR are calculated using (4)

It is noted that the number of +ve and –ve values placed in each row or column are equal except the rows which have MRS and MRL . Suppose the MRS is placed in a cell, say ( i, j ) of MRT then the number of +ve values to be placed in other cells of the i ^th row and j ^th column is always one less than the number of -ve values. Similarly, if MRL is placed in a cell ( k, l ) of MRT with i≠k and j≠l , then the number of –ve values to be placed in other cells of the k ^th row and l ^th column is always one less than number of +ve values. Once TR is found, the numbers to be filled in the cells of MRT are taken from [ -TR, TR ] and the average value for each cell is computed using (12)

avg va Ine = 2 Sp mxn - 2

2Sn

x

TR =

mm-2

Once avg_value is found, the sum of values to be filled in the rows and columns which do not have MRS and MRL denoted as Spr and Spc respectively are calculated using (13) and (14)

Here, the number 2 indicates that two cells of MRT are not filled because in that cells MRS and MRL are filled. It is noted that MRS and MRL are placed in such a way that either the same row or column should not have both MRS and MRL . After finding TR , the cell values in the interval denoted as V should have the numbers as in (5),

V = [-TR, TR] (5)

That is the process start with –TR , increment TR by 0.5, till it reaches TR after omitting 0. Thus half of the numbers in MRT are filled with +ve values and remaining half are filled with –ve values. To find each individual numbers to be filled in MRT, the negative numbers are computed using (6)

• r1- = - TR, r2- = r1- +0.5, r3- = r2- +0.5,… ,rTn- = -0.5(6)

and the positive numbers are computed using (7)

• r1+ = TR, r2+ = r1+ -0.5, r3+ = r2+ -0.5,… ,rTp+ = 0.5(7)

Then the total number of positive and negative numbers denoted as T_P and T_N are calculated using (8)

_c _ nxavg va lue

—2

x _

Sp C =------_----

Instead, for a row which has either MRS or MRL , the remaining sum of the values Spre and Spce are calculated using (15) and (16)

5pyg — (ⁿ -¹ )xavg_value

(m -1 )x avg   lue

Sp ce =------— ---- (16)

It is noted that for a row which has MRS, the corresponding row or column do not have equal number of +ve or –ve values. In that case only n/2 cells have –ve number and (n/2)-1 cells have +ve numbers. The numbers which are taken from V in (5) is selected using (17) in such a way that

T U! TV* = -^₌ 1 П ^-

Similarly, for a column the numbers are selected using (18)

-∑klrt =-∑(18)

Sprb =∑ ^Spri =  -2Spr(19)

Spcb =∑”=12 Spci =   -2Spc(20)

After calculating Sprb and Spcb using (19) and (20) respectively, the remaining values are taken from V , they are distributed in rest of the cells and their sum must satisfy (15) and (16). It is noted that sum of the values of all positive numbers and negative numbers in each row and column are zero after omitting MRS and MRL . Fig.1 shows the general form of MRT_mxn .The proposed MRT construction termed as MAWAGRT is shown in algorithm 1.

MRS +	r 12-	+ r13+	…	+ r1n-1+	-r1n-
r 21-	MRL	r23+	…	- r 2n-1	+ r2n+
			…
rm-11-	r m-12+	r m-13-	…	- r m-1 n-1	+ r m-1n
rm1+	rm2-	rm3+	…	+ r mn-1	- mn

Fig.1. General form of MRTmxn.

Algorithm1: MAWAGMRT (m, n, MRS, MRL)

//The algorithm considers the m, n, MRS and MRL as input and produces MRT mxn as output //

Begin {main}

• 1.    tot_cell ← (m*n-2)

• 2.    TR ← tot_cell/4

• 3.   V← [-TR, TR]

• 4.    Tp=Tn ← tot_cell/2

• 5.     read i, j, k, l

• 6.     i 1 ←i; j 1 ← j

• 7.    if (i≠k) then MRT(i, j) ← MRS

• 8.    if (j≠l) then MRT(k, l) ←MRL

• 9.   Sp ← 0; Sn ←0

• 10.   for i ← 1 to Tn do

• 11.   begin

• r i ⁺ ← TR – 0.5 ; Sp ← Sp + r i ⁺

• r i ^- ← -TR + 0.5; Sn ← Sn + r i ^-

• 12.   end {for i} 13.   ^9 value ← 2*Sp / tot_cell 14.  (a) If ((MRT(i, j)=MRstart) or (MRT(k,

• l)    = MRL)) then

begin

Spr ← n ^∗ ^9 value /2

Spc ← m ^∗ ^Q-value /2

Spre ← ( n - 1)∗ Qvalue /2

Spce ← (m- 1)∗^■^Svalite /2 end else

• (b)        for i ← 1 to n

• 15.    return MAWAGMRT

begin if (i≠i1) then locate the numbers from ri+ and ri-1 and form the elements in(MRT(i1, j))

such that sum(MR(i1, j)) ← Spr else sum(MRT(i, j)) ← Spre end {if} end {for i} for j ←1 to m begin if (j≠j1) then locate the numbers from ri+ and ri-1 and form the elements in(MRT(i, j1))

such that sum (MRT(i, j1)) ← Spc else sum(MRT(i, j1)) ← Spce end {if } end {for j}

end {main}

• B.    Construction of MR

After forming MRT_mxn, MRs is generated based on MRStart, MSSm . The steps involved are shown in algorithm 2.

Algorithm 2: MAWAGMR(m, MSSm, MRS)

// The algorithm considers the magic rectangle starting number MRS, number of rows m of magic rectangle m and order m magic sum as input and produces MRTmxn as output // begin (main}

• 1.    n← m+2

• 2.    Find r such that, 2^r ←m

• 3.   MST2sum← MSSm/2^r-1

• 4.   MRL←MST2sum-MRS

• 5.   MRT rxc ← MAWAGMRT (m, n, MRS,

• 6.    for i←1 to m

• 7.    for j ←1 to n

• 8.    if (MRT(i, j) < 0) then

• 9.   MRT(i, j) ← MRL-MRL * MRT(i, j)

• 10.  MRT(i, j) ← MRS+ MRS* MRT(i, j)

• 11.  return MAWAGMR

• 12.   end {main}

MRL)

else

• C.    Formation of Different MRTs from the Generated MR

After generating MRT, the generated MRT_m×n is called base MRT denoted as BMRT_{m×n .} Different MRTi_m×n, i=1,2,,,T_n, where T_n is total number of possible different MRT_m×n with the same magic sum and starting number are generated from BMRT_16×18 by interchanging within the rows and columns and Tn is calculated using (21)

T_n =       + Rowlnt         (21)

Where ColInt and RowInt denotes the number of possible interchange of columns and rows respectively and they are calculated using (22) and (23)

Colint =∑ ?=i  ( or ₎ (     - n       (22)

Rowlnt =∑ T=ij ( or ) ⁽ ^ - m (23)

It is noted that it enhances the security of any cryptosystems because each time different numerals are taken from MRTm×n for encoding the same character which occurs several times in a plaintext. As the numerals are different the cipher text obtained for the plaintext is also different so that the eavesdropper may not recover the plaintext from the ciphertext. The proposed algorithm 3 termed as MAWADMR describes the generation of different MRTs from BMRT.

Algorithm 3: MAWADMR ( BMRT, flag )

//This algorithm considers the BMRT and accepts the rows (columns) ri (ck) and rj (cl) are to be interchanged and makes the interchange in BMRT based on the rows and columns// begin {main}

• 1.  MR← MAWAGMR(m, MSSm, MRS)

• 2.    if (flag=1) then

• 3.    begin

• a.    read r₁, r₂

• b.    for i ←1 to m begin

BMRT[r 2 , i] ← MR[r 1 ,i]

BMRT[r 1 , i] ←MR[i,r 2 ] end

• c.    for i←1 to m

• d.      for j ←1 to n

• e.         if ((i≠r₁) and (j≠r₂)) then

• 4.    begin

BMRT[j, i] ←MR[i, j]

end {for j} end {for i} else

• a.    read c 1 , c 2

• b.    for j← 1 to n

begin

BMRT[j, c 2 ] ←MR[j,c 1 ]

BMRT[c 1 ,j] ←MR[c 2 ,j] end

• c.    for i ← 1 to m

• d.      for j ← 1 to n

• e.        if ((i≠c 1 ) and (j≠r 2 )) then

• 6.    end{main}

BMRT[j, i] ← M R[i, j]

end {for j} end {for i} 5.   return BMRT

Once the MR and interchanged MRs are generated, the numeral from them are located based on the ASCII value of the character m i and it is treated as the position in MR. Let it be ASi . Then, the corresponding numerals retrieved from MR is calculated using (24)

MR(ASi) = (int(ASi)/n)+ mod(ASi/n)       (24)

• D.    Proposed Methodology for Construction of MRT– An Example

To show the relevance of the work, let m= 6 and n=8. Then TR is calculated as,

6 x 8-2

48 - 2

11.5

And

V = [-11.5, 11.5]

6 x 8  48

Now , Tp =   = ₂ = ₂ =24

Thus r1-= - 11.5, r2-= -11.0, … , r24- = -0.5

r1+= 11.5, r2+= 11.0, … , r24+ = 0.5

Then,

Sp = ∑?=i™+ = 11.5 + 11.0 + ⋯ + 0.5 = 138

Sn=∑?=i™ =-11.5-11.0-⋯-0.5 = -138

And ∑ ^ri* _-∑ ^i^i = 138 -138= 0

avg _ value = ⁽ 138 ⁾ = =6

If the rows and columns do not have MRS and MRL , then

8×6

Spre =  ₂  =24

6×6

Spce =  ₂  =18

If a row has MRS or MRL then,

∑ ri

-

^∑ ГГ

= 21

=

7×6

= 21

=

5×6

= 15

-

^∑ ГГ =∑ri

= 15

Based on these calculations, the general form of MRT_6x8 is shown in fig.2. Similar type of computations can also be performed in generating MRT_16x18 .

MRS	7.0	-7.5	11.5	-5.5	2.5	-5.0	-3.0
-7.0	MRL	7.5	-11.5	5.5	-2.5	5.0	3.0
9.0	-9.0	11.0	-10.0	8.5	-10.5	2.0	-1.0
-4.5	4.5	-11.0	10.0	-8.5	10.5	-2.0	1.0
6.0	-6.0	9.5	-8.0	4.0	-6.5	1.5	-0.5
-3.5	3.5	-9.5	8.0	-4.0	6.5	-1.5	0.5

Fig.2. MRT6×8

• E.    Proposed Methodology for Construction of MR – Example

  In order to understand the relevance of the work let the magic sum = 7800, MRS=4, m=16 . Then n=18, 2 ⁴ =16 . Thus l=4 and k=3 . MST2sum=7800/8= 975 . Now MRT 16×18 csum= 7800, MRT 16×18 rsum= 7800 + 975=8775 and MRL = 975-4=971. Suppose MRS and MRL are placed in MRT 16×18 (1, 1) and MRT 16×18 (3, 2) respectively. Then using algorithm 2, a MRT_16×18 is generated and it is shown in fig. 3.

4	16	24	967	963	951	931	44	893	82	122	853	162	813	202	773	282	693
18	6	955	961	965	20	40	935	909	66	106	869	146	829	186	789	266	709
959	971	22	12	8	953	42	933	919	56	92	883	136	839	176	799	256	719
969	957	949	10	14	26	36	939	68	907	8S	887	128	847	198	777	248	727
48	38	30	943	941	925	947	28	74	901	867	108	158	817	192	783	278	697
927	937	945		34	50	929	46	62	913	891	84	152	823	212	763	77 7	703
SO	70	64	60	58	899	S97	921	923	903	861	114	811	164	771	204	234	741
895	905	911	915	917	76	78	54	52	72	873	102	831	144	791	184	228	747
98	110	90	112	118	94	855	859	871	875	S79	SS9	845	130	SOI	174	691	284
877	865	885	863	857	881	120	116	104	100	96	86	841	134	779	196	711	264
170	160	126	138	140	148	S09	807	851	843	833	825	819	156	781	194	725	250
805	815	849	837	835	827	166	168	124	132	142	150	821	154	761	214	721	254
210	200	17S	ISO	188	226	218	220	769	767	803	793	785	753	759	751	699	276
755	775	797	795	787	749	757	755	206	208	172	182	190	777	216	224	761	274
290	280	246	260	268	258	242	236	689	687	731	723	713	705	735	737	743	232
685	695	729	715	707	717	733	739	286	288	244	252	262	270	240	238	745	230

Fig.3. MR16×18with row sum = 8775, column sum=7800and starting number= 4

• IV.    MR Based Public key Cryptosystems

It consists of two phases, in phase 1 assignment of MR numerals to the plaintext is performed and in phase 2 the encryption/decryption is performed using the numerals obtained in phase 1.

• A.    Assignment of MR Numerals to the Plaintext

Let the message to be encrypted is M and its length is L(M) . For each m i ϵ M, i= 1,2,…,k where k is the number of different characters occur in M . Also let m 1 , m 2 ,…,m k occurs n 1 ,n 2, ...,n k times respectively. Moreover,

Z^ ,n = LW          (25)

Before encrypting any M , first encoding of m i is performed. For that ASCII(m i ) is taken. Let it be AS i . Then AS i is considered as the positional value and the numeral which occurs at that position is taken from MRT_i . As m_i occurs n_i times, the BMRT is interchanged with rows/columns by n_i times and hence for the same m_i different numerals are obtained from MRTi . Only BMRT is shown in fig.3 and the remaining (n_i-1) MRTs are created virtually. Let the numeral taken from MRT_i is denoted as IpMRT i (m i ) . To interchange the rows, two random numbers r 1 and r 2 are taken where r 1 , r 2 ≤ m . Similarly for interchanging the columns, two random numbers r 3 and r 4 are selected such that r 3 , r 4 ≤ n .

• B.    Assignment of MR Numerals to the Plaintext- An Example

For example let the message M to be encrypted is

“KANNAN BABA”. Now, L(M)= 11, m 1 = ‘K’, n 1 = 1; m₂= ‘A’, n₂=4; m₃= ‘N’, n₃=3; m₄= ‘B’, n₄=2;m₅= ‘BLANK’, n₅=1. In order to encrypt ‘A’ first ASCII (‘A’) = 65 is taken. Then, the numeral which occurs at 65^th position in BMRT is 88 for the first time. Thus, IpMRT₁(m₁) = ‘88’. To get another numeral for ‘A’ in the second time, suppose column interchanging is followed. For that, let the r 3 and r 4 are selected as 6 and 11 respectively and hence column 6 and 11 are interchanged. Now IpMRT 2 (m 1 ) = ‘847’. For the third time let r 3 and r 4 are chosen as 12 and 14 that is column 12 and 14 are interchanged. Now   IpMRT₃(m₁) =  ‘847’. Similarly,

IpMRT4(m1)=  ‘847’. Similar process can also be performed for encoding other characters too.

• C.    RSA Encryption/ Decryption with MRT

The RSA encryption/decryption is modified with MRT is as follows. In RSA, the keys are based on the modulus n = pq, ɸ(n)=(p-1)(q-1). Select e, 1MST2sum. To encrypt, for each mt6M, first find IPMRi(mi)  =  MRi(ASi) where IPMRi(mi)    is intermediate plaintext mi obtained from MRi.  To get ci, ci= [IPMRi(mi)]e mod n. To decrypt, IPMRi(mi)= cid mod n. After obtaining IPMRi(mi), first locate the position from MRi in which IpMRi(mi) is occurring. It is considered as ASCII value. Let it be ASi. Then, mi= CHR(ASi).

• D.    RSA Encryption/ Decryption with MR- An Example

In order to get proper understanding of the modified

RSA, let p=53, q=59 and n is computed as n=3127> 975(=MST2sum) . The public key of a user is (7, 3127) and the private key is (431, 3127). Let the message M to be encrypted is “KANNAN BABA”. Then I P MR 1 (m 1 )=30,c i =30 ⁷ mod 3127=23 . To decrypt, I P MR 1 (m 1 )=23 ⁴³¹ mod 3127=2779, AS 1 =I P MR 1 (m 1 )=75, m 1 =CHR(AS 1 )=”K” . Similar process can also be performed for other characters of plaintext too. Table 1 and Table 2 show RSA encryption and decryption with MRT respectively.

Table 1. RSA Encryption with MRT

S. No (i)	Plain Text m I ∈ M	AS i = ASC II (m i )	Interchanged (Row i , Row j ) or (Col k ,Col l )	MRT i	Ip i = I P M R i (AS i )	Cipherte xt Ci=Ip i7 mod 3127
1	K	75	*	MRT 1	30	2779
2	A	65	*	MRT 1	88	2472
3	N	78	*	MRT 1	925	2156
4	N	78	(6,11),(12,14)	MRT 2	108	3096
5	A	65	(6,11),(12,14)	MRT 2	847	1854
6	N	78	(6,14),(3,11)	MRT 3	867	2200
7	Blan k	32	*	MRT 1	829	2305
8	B	66	*	MRT 1	827	2774
9	A	65	(6,14),(3,11)	MRT 3	949	3018
10	B	66	(6,11),(12,14)	MRT 2	26	1231
11	A	65	(10,11)	MRT 4	907	2852

*- indicates no interchange of rows and columns

Table 2. RSA Decryption with MR

S.No.	c i	I Pi = C i431 mod 3127	MR i	AS i	PlainText m I ∈ M
1	2779	30	1	75	K
2	2472	88	2	65	A
3	2156	925	3	78	N
4	3096	108	4	78	N
5	1854	847	5	65	A
6	2200	867	1	78	N
7	2305	829	2	32	Blank
8	2774	827	3	66	B
9	3018	949	4	65	A
10	1231	26	5	66	B
11	2852	907	6	65	A

Similarly, the same kind of calculations can be performed for ElGamal encryption and decryption with MRs.

• V.    Results and Discussion

The proposed methodology is implemented in VC++ with version 6.0. Parallelism is performed with different processors viz., 1, 2, 4, 8 and 16 in a simulated environment with Maui scheduler which uses back filling philosophy. Before performing encryption/decryption different MRs are generated with the same magic sum, starting number and the encoding of plaintext is done based on the numerals available in MRs. After encoding the plaintext, the modified ElGamal (not shown here) and RSA algorithms are taken for encryption and decryption as illustrated in section 4. The process is repeated for different file sized message viz., 1 MB, 2 MB, 3MB, 4MB and 5MB respectively and the time taken for encryption and decryption with RSA and ElGamal is computed and they are shown in Table 3 and Table 4 respectively. Table 5 and 6 show the time taken for the same without MR.

Table 7 and Table 8 represent the ratio of encryption and decryption time taken by the processors 2 ^k /2 ^k-1 where k=1,2,3,4 with the same file size. It is evident from Tables 7 and 8 that the time taken for encryption/decryption is substantially reduced as the number of processors is increasing. The time taken for both encryption/decryption of RSA and ElGamal is decreasing and the number of parallel processors are increasing. In a simulated environment the speed of RSA cryptosystems are somewhat high when the same is compared with ElGamal. This is because in ElGamal encryption, the ciphertext produced is always in double which results in decreasing the speed when the same is compared with RSA. In order to measure the security level of RSA and ElGamal cryptosystems with and without MR, All Block Cipher (ABC) Universal Hackman tool is used in this work and the security levels produced by the said algorithms are shown in Table 9 and Table 10 and their corresponding graph are shown in Fig. 4. It is evident from the Tables 9 and 10 that RSA, ElGamal with MR outperforms than the original RSA and ElGamal.

Table 3. RSA Encryption/Decryption with MR

FS (MB)	No. of. Processors (MR-RSA)
	1		2		4		8		16
	E ms	D ms	E ms	D ms	E ms	D ms	E ms	D ms	E ms	D ms
1	2468	2421	1247	1275	653	674	432	341	212	219
2	4242	4267	2177	2209	1071	1188	539	648	339	403
3	6398	6410	3162	3249	1683	1642	947	942	596	485
4	8809	8716	4486	4385	2298	2217	1081	1120	653	625
5	10862	10982	5548	5463	2722	2858	1371	1398	864	764

FS- File Size E- Encryption Time D- Decryption Time

Table 4. ElGamal Encryption/Decryption with MR

FS (MB)	No. of. Processors (MR-ELG)
	1		2		4		8		16
	E ms	D ms	E ms	D ms	E ms	D ms	E Ms	D ms	E ms	D ms
1	2991	2995	1564	1588	828	798	378	493	212	302
2	5076	5376	2647	2770	1386	1329	652	797	339	485
3	8071	7913	3986	4106	2172	2131	999	986	596	578
4	10842	10782	5432	5456	2747	2827	1503	1373	653	782
5	13689	13727	6752	6865	3366	3446	1860	1742	864	873

Table 5. RSA Encryption/Decryption without MR

FS (MB)	No. of. Processors (RSA)
	1		2		4		8		16
	E ms	D ms	E ms	D ms	E ms	D ms	E ms	D ms	E ms	D ms
1	2077	2091	1126	1093	572	566	364	329	220	261
2	3652	3725	1839	1847	1038	999	579	612	246	249
3	5427	5571	2782	2860	1451	1407	691	775	421	449
4	7625	7527	3772	3879	1978	1886	1073	1093	542	583
5	9376	9653	4819	4782	2443	2351	1264	1213	711	721

Table 6. ElGamal Encryption/Decryption without MR

FS (MB)	No. of. Processors (ELG)
	1		2		4		8		16
	E ms	D ms	E ms	D ms	E Ms	D ms	E ms	D ms	E ms	D ms
1	2799	2620	1440	1434	697	810	441	425	212	267
2	4742	4910	2431	2481	1260	1212	611	594	339	320
3	7156	7208	3642	3724	1923	1834	1041	968	596	508
4	9788	9907	5022	4994	2434	2599	1334	1272	653	667
5	12316	12359	6238	6136	3144	3140	1587	1580	864	901

Table 7. Ratio for the Processors 2^k/2^k-1 with RSA and MR-RSA Encryption

RSA Encryption Without MR						RSA Encryption With MR
FS R	1 MB	2 MB	3 MB	4 MB	5 MB	FS R	1 MB	2 MB	3 MB	4 MB	5 MB
1/2	1.84	1.98	1.95	2.02	1.94	1/2	1.97	1.94	2.02	1.96	1.95
2/4	1.96	1.77	1.91	2.90	1.97	2/4	1.90	2.03	1.87	1.95	2.03
4/8	1.57	1.79	2.09	1.84	1.93	4/8	1.51	1.98	1.77	2.12	1.98
8/16	1.65	2.35	1.64	1.97	1.77	8/16	2.03	1.58	1.58	1.65	1.58
Tot.	7.02	7.90	7.60	7.75	7.62	Tot.	7.43	7.55	7.26	7.69	7.56
Avg.	1.75	1.97	1.90	1.93	1.90	Avg.	1.85	1.88	1.81	1.92	1.89

FS- File Size      R- Ratio

Table 8. Ratio for the Processors 2^k/2^k-1 with RSA and MR-RSA Decryption

RSA Decryption Without MR						RSA Decryption With MR
FS R	1 MB	2 MB	3 MB	4 MB	5 MB	FS R	1 MB	2 MB	3 MB	4 MB	5 MB
1/2	1.91	2.01	1.94	1.94	2.01	1/2	1.89	1.93	1.97	1.98	2.01
2/4	1.93	1.84	2.03	2.05	2.03	2/4	1.89	1.85	1.97	1.97	1.91
4/8	1.72	1.63	1.81	1.72	1.93	4/8	1.97	1.83	1.74	1.97	2.04
8/16	1.26	2.45	1.72	1.87	1.68	8/16	1.55	1.60	1.94	1.79	1.82
Tot.	6.82	7.95	7.52	7.59	7.67	Tot.	7.32	7.23	7.63	7.73	7.79
Avg.	1.70	1.98	1.88	1.89	1.91	Avg.	1.83	1.80	1.90	1.93	1.94

Table 9. Security level of RSA without and with MR (in percentage)

File Size (MB)	No. of Processors					File Size (MB)	No. of Processors
	1	2	4	8	16		1	2	4	8	16
1	76	78	76	77	78	1	87	89	88	91	91
2	78	78	76	76	76	2	87	89	89	87	89
3	78	76	78	78	77	3	87	87	87	87	88
4	78	77	76	76	78	4	89	89	87	89	88
5	77	77	77	78	77	5	88	89	88	87	88
Tot.	387	386	383	385	386	Tot.	438	443	439	441	444
Avg.	77.4	77.2	76.6	77	77.2	Avg.	87.6	88.6	87.8	88.2	88.8

Table 10. Security level of ElGamal without and with MR (in percentage)

File Size (MB)	No. of Processors					File Size (MB)	No. of Processors
	1	2	4	8	16		1	2	4	8	16
1	87	86	89	87	87	1	95	93	94	95	95
2	87	87	87	85	87	2	95	94	95	93	93
3	85	86	85	87	87	3	95	94	95	94	95
4	85	87	87	85	85	4	93	94	94	93	93
5	87	85	86	85	85	5	94	94	93	95	95
Tot.	431	431	434	429	431	Tot.	472	469	471	470	471
Avg.	86.2	86.2	86.8	85.8	86.2	Avg.	94.4	93.8	94.2	94	94.2

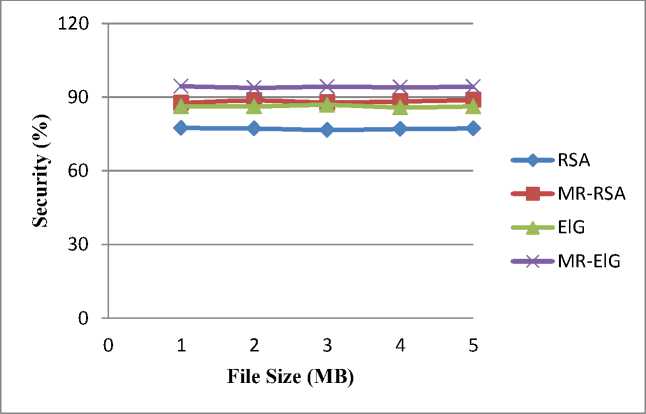
Fig.4. Graph for Security level of RSA and ElGamal without and with MR

• VI.    Conclusion

An alternate encoding scheme based on MR instead of existing ASCII based encoding scheme has been thought of and the numerals involved in MR are used for encryption in RSA and ElGamal  public-key cryptosystems. The numerals are not easily tracked by the eavesdropper because the magic sum, MRS and MRT used in generating the MR are only known to the sender and the receiver. Additionally, for the same magic sum different MRs is generated by interchanging rows or columns which will produce different numerals at the same position every time. This causes an additional layer of security for any cryptosystems before performing encryption  and  decryption. Further,  to speedup cryptographic operations parallelism is used in this paper which is  based  on Maui  scheduler  in  simulated environment with different processors. For RSA encryption and decryption without MR the speed is increased around 1.89 and 1.88 times respectively when the number of processors is increased. Then for RSA encryption and decryption with MR the speed is increased around 1.87 and 1.85 times respectively. For ElGamal encryption and decryption without MR the speed is increased around 1.92 and 1.89 times respectively. Then for ElGamal encryption and decryption with MR the speed is increased around 1.97 and 1.91 times respectively. Further, the security level of RSA and ElGamal without MR is 77.08 and 86.24 when RSA and ElGamal cryptosystems are incorporated in MR the security level is 88.02 and 94.12 respectively.