Ergodic Matrix and Hybrid-key Based Image Cryptosystem

Published Online June 2011 in MECS

Transmitting information through the internet has been a mainstream task in modern life for these reasons: geographical position independence, fast speeds, and low costs. However, while we are taking the advantage of the internet, unauthorized individuals can purloin the images for processing, distributing or replicating. Hence information security is an important problem. Therefore cryptography plays a vital role in many fields, such as mobile phone communications, sending private emails, security of bank cards, online payments, users’ passwords, online personal photograph albums and other touches of our daily lives [1]. Cryptography is a technique of transforming plaintexts into ciphertexts and retransforming the messages back to the original form. Modern cryptography involves not only the disciplines of mathematics but also computer sciences and engineering.

Image cryptography has various applications in telemedicine, military image database and multimedia Copyright © 2011 MECS systems, etc. Although there are many cryptosystems, such as RSA, DES, IDEA, SAFER and FEAL, which can be used to encrypt images, these are not ideal for two reasons [2]. One is that the image size is generally much greater than that of text. This results in conventional cryptosystems taking much more time to encrypt images directly. The other reason is that image data has high correlation among adjacent pixels. Consequently, it is rather difficult for these cryptosystems to shuffle and diffuse image data effectively.

By and large, there are two main schemes that can be used to protect digital images:

• (1)    Information hiding, which is a technology that uses anonymity, watermarking, covert channel and steganography; and

• (2)    Encryption, which includes traditional encryption and other such as chaotic encryption [3-4].

Chaos-based cryptosystems usually have higher speeds and lower costs. Moreover, these systems are sensitive to initial conditions and control parameters. These optimistic characters make them suitable for image encryption. In this respect, during the past decade a great number of chaotic systems have been proposed. For example, Chen et al. used a 3D baker map [6] and a 3D cat map [7] in the permutation process. Guan et al. employed a 2D cat map for substitution and the diffusion of Chen’s chaotic system for masking the pixel values [8]. Jiri Giesl et al. used the chaotic maps of Peter de Jong’s attractor to improve the chaos image encryption speed [5]. Yang et al. introduced a keyed hash function to generate a 128-bit hash value so that the scheme could be used to encrypt and authenticate [9].

However, the deficiencies of these chaos-based cryptosystems can be summarized as below:

• (1)    The communication session is mostly based on symmetric cryptography.

• (2)    Lack of authentication, which means it is difficult for the receiver to confirm that the cipher image is sent by the one he wants to communicate with.

The disadvantage of symmetric cryptography is that it

I.J. Image, Graphics and Signal Processing, 2011, 4, 1-9

presumes two parties have agreed on a key and been able to exchange that key in a secure manner prior to communication. Since the cipher key is public, the distribution and management of keys are much simpler, i.e. in a population of n people the total keys are 4 n . For this reason, the requirements for key exchange make symmetric cryptosystems difficult to use. In addition, the distribution of keys remains the biggest challenge in the use of cryptosystems of this kind [12].

Asymmetric (also called public-key) cipher is noticed as the most significant new development in cryptography in the last 30-40 years [25]. It is a technique employed by many cryptographic algorithms and cryptosystems. Its feature lies in the asymmetric key algorithm, where the key used to encrypt a plain-text is different from the key used to decrypt it. Each user holds a pair of cryptographic keys – public keys and private keys [21-22]. The public keys can be distributed whilst the private key is kept secret. Plain-texts are encrypted with the recipient’s public key and can be uniquely decrypted with the private key held by the recipient. This thought came from the publication of “New Directions in Cryptography” by Diffie and Hellman in 1976.

However, in practice, the asymmetric-key cryptography system has not replaced the symmetric-key cryptography system. Though the asymmetric-key encryption system is based on sophisticated mathematical problems (its calculation is very complicated and makes it more secure), its speed is also far slower than symmetric-key encryption systems. As a result, in practical applications we can make use of the advantages of both these two algorithms, using symmetric algorithm to encrypt files and asymmetric algorithm to encrypt the keys of the encrypted document key (or it may be called session key ), which is a hybrid encryption system. This provides a better way to solve the computing speed issues and the key distribution and management issues.

To realize the hybrid image cryptosystem, ergodic matrix shall be used in this paper. Zhao et al. [10-11] have proved some theorems of ergodic matrix; it is said that the matrix has large period over F9. This profound property makes it feasible in the image encryption process.

The rest of this paper is organized as follows: Section 2 gives the background about ergodic matrices; Section 3 is devoted to the description of the proposed image encryption and authentication scheme; the security of this scheme is tested in Section 4; Section 5 analyzes the performances; and finally, some conclusions and future works are drawn in Section 6.

• II.    Overview of ergodic matrix

Ergodic matrix was introduced by Zhao et al. [10-11]. The basic idea can be briefly described as below:

Let F9 be a set of all nxn matrices over the finite nXn field F9, (FffAn, +, x) form a 1-ring, here + and x are addition and multiplication over F9, respectively. We randomly generate two nonsingular matrices Q 1,Q2e F9 , then: nA n

• (1)    (F f_An , x ) is a monoid, its identity element is I _nxn ,

• (2)    « Q 1 ) , x ) and « Q ₂ ) , x ) are Abelian groups, their identity elements are also I_nxn . Here Q 1 , Q ₂ are nonsingular and Q 1 , Q ₂ E F f_An , and

• (3)    for any m 1 , m ₂ E F L_An , generally m 1 x m 2 ^ m ₂ x m 1 . i.e. the multiplication is not commutative in F f_An .

Ergodic matrix has the following definitions and properties:

Definition 1: Given Qe F9 if V ve F9   \{0}, nAn            nX 1

{ Qv , Q ² v , ... ,Q⁹ " ^-1 v } just takes over f L_a1 \{ 0 }, then Q is what so-called ergodic matrix over finite field F⁹. (Here 0 =[0 0 ... 0]^T)

Definition 2: Given Q ё Р П_хл , if ( Q ) = { Q | x = 1, 2, 3,^}, then { Q ) is the generating set of Q over F L_xl .

Theorem 1 : Q e F n_xn is an ergodic matrix if and only if the order of Q is ( q ⁿ -1) after the multiplication of Q over finite field F⁹.

Theorem 2 : Given n and ( q ⁿ -1) are coprime, g ＝ ( g n … g ₂ g 1 ) e ( F⁹) ⁿ Л ( g_n # 0), given Q is an ergodic matrix, then (F⁹ [ Q ],+, • ) constructs a field of q" elements, { Q 0 = I , Q 1^, Q ^-1} is a basis of F⁹[ Q ] over F⁹.

Lemma 1 : For V v e F⁹[ Q ], there is unique a ₀, a 1, . . , a _n-1 e F⁹ such that v = a ₀ 1 + a 1 Q + a ₂ Q ² + . + a _n-1 Q " ^-1.

Theorem 3 : Given Q e F n_xn is an ergodic matrix, Q ^T must be an ergodic matrix as well.

Theorem 4 : Given Q e F n_xn is an ergodic matrix, then for V v e F n_x1 \{ 0 }, { v ^T Q , v ^T Q ², ... , v ^TQ⁹ " ^-1 } just takes over { v H v e F Lxi }\{ 0 ^t }.

Theorem 5 : Given Q e F n_xn is an ergodic matrix, there are ^ ( q " -1) ergodic matrices in ( Q ) ( ^ ( x ) is Euler function). These ergodic matrices have the same generation set.

Definition 3 : Ergodic matrices are equivalent if they have the same generation set.

From the theorems above, over finite field F⁹, all n x n ergodic matrices have the same order and their generating sets have the same size, which are larger than that of any other n × n non-ergodic matrices. Take a random ergodic matrix Q e F |oX_5o as an example, then the image of the matrix and the histogram is shown in Fig. 1.

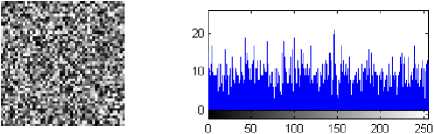
(a)                                     (b)

Figure 1: The image of a random ergodic matrix Qe F |„X_so and the corresponding histogram (a) Image of random ergodic matrix, (b) Histogram of the corresponding ergodic matrix

This figure implies that an ergodic matrix is almost uniformly distributed, thus it can be used to encrypt an image.

• III.    The proposed image encryption algorithm

Fridrich suggested that an image encryption scheme should be composed of confusion and diffusion [4]. The confusion process permutes all the pixels without changing their values, which make it difficult to resist statistical attacks. Then in the diffusion process, the pixel values are modified such that a tiny change, for instance, the value of one pixel increased by only 1 bit, will spread out to all pixels in the cipher-image.

• A.    Communication process

The communication process is composed of encryption, decryption and authentication.

In consideration of the basic need of cryptology, the cipher-text should have close connection to the key. There are two ways to realize this requirement [20]: one is to utilize a good key generation mechanism, another is to thoroughly mix the key with the plain-text in the encryption process.

Therefore, to realize the hybrid-based cryptosystem that satisfies the requirement, we carry out the process as below:

• (1)    Alice and Bob respectively take ( x a , y a = f ( x a , k a )) and ( x b , y b = f ( x b , k b )) as public-keys, k a and k b as privatekeys. Here x a = Q a , y a = f (x a , k a ) = Q a ^k a ; x b = Q b , y b = f ( x b , k b ) = Q b k b .

• (2)    When Alice wants to communicate with Bob, she generates a random key k_x e K and computes K 1 = f ( x b , k_x ) = Q b k x , K a = f y b , k x ) = Q b k b k x . Then she gets CID a by encrypting her identity ID a with K 1 . For example, she encodes her identity information into an n –order matrix, then XOR with K 1 , or gets CID _a by K 1 x ID _a = Q _b kx ID _a. After this, she sends ( CID a , K a ) to Bob.

• (3)    Bob uses his own key k b to deduce K 1 = f ( K a ,- k b )=( Q b ^kbkx ) Q b ^{- kb} = Q b ^kx and decipher ID a by XOR CID a with Q _b ^kx , or by the equation ID _a = K 1 ^-1 x CID _a, thus he gets Alice’s public-key ( x a , y a ) and makes sure CID a is actually from Alice.

• (4)    Bob generates a random key k_ye K , and computes K 2 = f (x a , k y )= Q a k^y , K b = f y a , k y )= Q a ^k a ^ky , CK b = f K 1 , K b ) = Q b ^kx Q a ^kaky . Then he sends CK b to Alice.

• (5)    Alice decrypts K _b and K ₂ by K _b= f ^-1 ( CK _b, K ₁), K ₂= f ^-1 ( K _b, sk _a). Thus K ₁ and K ₂ can be used as session keys between Alice and Bob.

• (6)    If Alice wants to secretly send an image to Bob, she may encrypt the image by one of the session keys. Take K 1 for example, then she gets the cipher-image by Cimg= f ( K 1 , image) = f ( Q b ^kx , image).

• (7)    Bob deciphers the image by Dimg = f ^-1( K 1 , image) = f ^-1( Q b ^kx , image).

• B.    Confusion

The confusion (also called discretization, permutation) stage shuffles the pixels in the image. It is an important technique used in image encryption and information hiding. Scientists have been conducting investigations in this field for a long time. Typical approaches to confusion include Arnold permutation [13], Hilbert permutation [14], Kolmogorov flows [15], baker map [16], Knight’s tour problem [16-17], standard map [18], etc.

These existing techniques imply that an effective algorithm for confusion should follow the principles as below:

• (1)    Transform T must be 1-1 map. This is the primate premise for confusion. Only by following this rule can we make sure each pixel of cipher image will not lose its original information, so that it can be completely decrypted.

• (2)    T must disorganise the correlated positions of the plain-image as much as possible, such that the cipherimage cannot be directly seen by the human eyes or be guessed the information of the original image.

• (3)    T can rapidly disorganise the correlated positions of the plain-image; this is an important measure of the efficiency of a confusion algorithm.

• (4)    The existing cryptosystems and the fast speed of computers make it difficult for any cipher-image to resist the brute-force attack. For the security of the encryption algorithm, key space is needed to be as large as possible.

As a result, based on the discretization property of ergodic matrix, we propose a confusion scheme that goes by the following steps:

First, given Q b ^kx is the key to encrypt the image, if the size of Q _b ^kx is smaller than that of the image, Alice calculates the power of Q _b by the following algorithm:

• ® H and W are the height and width of the image respectively;

® N is the number of the elements of the key Q _b kx ;

@ n rounds the elements of HxW/N to the nearest integers greater than or equal to H×W/N;

@ ArrayB stores the result of n matrices that Alice calculates;

® IX=sort(ArrayB) returns an array of indices after sorting ArrayB.

Then Alice discretizes the image according to IX. For example, if IX(i)=37, the i-th pixel of the image is put to the 37th position.

The experimental result for this discretization algorithm is shown in Figure 2.

(a) Original Lena image                    (b) Permuted image

Figure 2: Comparison of images after 1-round of permutation

It is easy to prove that this discretization is 1-1 map, which satisfies the 1st principle above. Furthermore, the permuted image disorganizes the plain-image as much as possible so that it is hard to recognize, which satisfies the 2nd principle.

• C.    Diffusion

Shannon suggested employing diffusion and confusion in the cryptosystem [24]. The diffusion stage is necessary because an attacker can break the system by comparing a plain-image and corresponding cipher-image to discover useful information. For the purpose of diffusion, an explicit function which uses the ergodic matrix and the “XOR plus mod” [18] operation will spread out the influence of a single pixel, which is from the plain-image, over many cipher image pixels. This is detailed below.

Respectively choose the first element from Q b ^kx and the plain-image as initial value.

Q b ^kx is designed as M ( k ) and is XOR-ed with the values of currently operated pixel (from the plain-image) and previously operated pixel (from the cipher-image), according to formula (1) below:

C (k) = M ( k ) ⊕ {[ I ( k ) + M ( k )] mod CLevel } ⊕ C ( k- 1) (1) where I ( k ) is the currently operated pixel, CLevel is the colour level (for the image used to test, CLevel=256) of the image and C ( k- 1) is the previously output pixel of the cipher-image. Bob may inverse the transform of the above formula as formula (2).

I ( k ) = {[ M ( k ) ⊕ C (k) ⊕ C ( k- 1) + CLevel - I ( k ) } mod CLevel. (2)

We can see that the corner pixel C (1) (namely, the position (1,1) in the image) is not diffused at all under this algorithm. Besides, one pixel change in the image may not alter the cipher-image much, especially if the change is in the last pixel (namely the position is (512,512)). Hence another diffusion stages from the last pixel in the image is needed.

The experimental result for this discretization algorithm is shown in Figure 3.

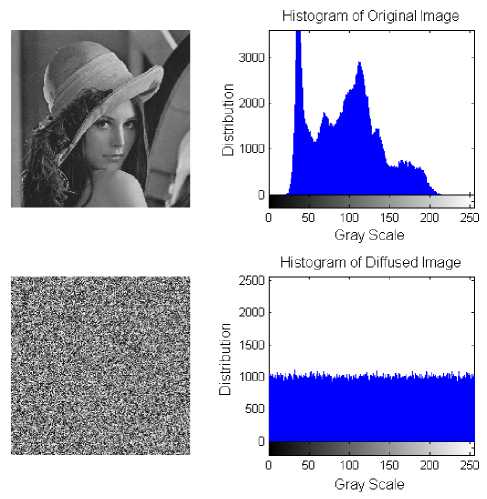
Figure 3: Comparison of images after 1-round of diffusion

IV. Security analysis

All tests in this paper are conducted on the 512×512 Lena image with 8-bit gray scale. The diffusion round is 2, whilst the confusion round is 1.

• A.    Key space analysis

The key space of any cryptosystem should be satisfactorily large enough to resist brute-force attack. In this proposed public-key based image encryption algorithm, key ( x a , y a = f ( x a , k a ) and ( x b , y b = f ( x b , k b )) are solely employed for encryption and decryption. Hence the key space primarily lies on the size of ergodic matrix (meaning unclear). For an n × n ergodic matrix over finite field F⁹ , the number of non-equivalent matrices is calculated by fomula (3) [23]:

^ л^

П Г^ПЗ^Д = (^ ” - ^ⁿ - ^²) ^(^ ” - ^  )/ⁿ (3)

In the experiments we utilize a 50×50 ergodic matrix over finite field F256, thus the key space is so-1 25650 - 256*

^ 50 x (2 5 6 50 - 1)

*=o « 3.08 x 10⁵⁸⁹⁸

This is quite large thus it is sufficient for practical use and can resist all kinds of brute force attack.

The reason for the immense key space in the proposed scheme is that the session keys are n × n matrices, of which the range of each element is [0, 255].

From Lemma 1, any ergodic matrix Q e F n_xn can be denoted by an n -vector over F⁹. Thus the size of the matrix Q e F 50X_5o used in the experiment can be reduced to 50 bytes from 2500 bytes.

• B.    Statistical analysis

(1)    Histogram analysis

We can see from Figure 3 that after 1-round diffusion, the histogram is fairly uniform and does not reveal any statistical information of the plain-image.

(2)    Correlation of two adjacent pixels

The high correlation of adjacent pixels is fragile to resist statistical cryptanalysis. As a result, a secure encryption scheme, which can eliminate the correlation between adjacent image pixels, is needed. Hence to calculate the correlation of two adjacent pixels, formula

(4) is carried out:

cov(x,y)

=      Z f=ito - Eto) X (y - E⁽y⁾⁾      (4)

" V^M- ВД)² X 7Z f₌i (y _/ - E(y))^{2 1}

where E(x)=-£f=1x, R is the number of pairs of the adjacent pixels selected in the test. This formulate indicates -1≤cov(x, y)≤1, which means with cov(x, y) getting closer to 0, the correlations of two adjacent pixels will be less.

The experiment was divided into 10 groups and each group has 10,000 pairs of pixels, i.e. R =10,000. The correlation distributions of two adjacent pixels in the cipher-image are tested respectively in horizontal, vertical and diagonal. Table 1 shows the results of the correlation coefficients of our proposed algorithm.

The mean correlation coefficients for our algorithm Table 2. and the comparisons with other algorithms are listed in

T able 1. C orrelation coefficients of two adjacent pixels in the cipher - image

Horizontal	-0.00563	0.00021	-0.01433	-0.00089	-0.0018	-0.00207	-0.00388	0.010665	0.013546	0.011906
Vertical	0.0033113	0.015407	0.0071656	-0.000164	-0.000174	-0.008530	-0.004694	-0.003341	0.0001274	0.010477
Diagonal	-0.004935	0.009473	0.0011877	-0.008290	0.016918	0.0018506	-0.005332	0.01446	0.0040661	-0.01054

T able 2. C orrelation coefficients compared in two algorithms

	Plain-image	Cipher-image (Proposed, mean value)	Cipher-image (Yang et al. [9])	Cipher-image (Ye G. [26])	Arnold method ([26])
Horizontal	0.98024213	0.006493	0.002097	-0.0134	0.0787
Vertical	0.97533157	0.005339	-0.016187	0.0012	-0.0793
Diagonal	0.96573878	0.007705	0.017805	0.0398	-0.0633
Average	0.97377083	0.006512	0.01203	0.0181	0.0738

Both experiments utilized 512×512 Lena image with 256 gray scales. It is easy to see that the result of our algorithm is much closer to 0. This indicates that our algorithm has effectively removed the correlation of adjacent pixels in the plain-image, thus it is better for image confusion and diffusion.

Test results for correlation of adjacent pixels are shown in Figure 4:

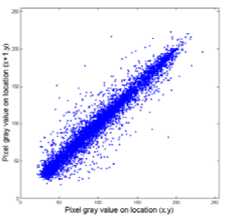
(a) The plain-image

Figure 4: correlation of two horizontally adjacent pixels in (a) and (b)

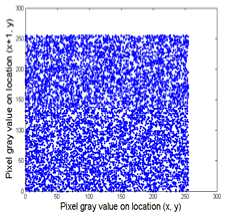
(b) The cipher-image

Results imply that it is very difficult to deduce secret key from cipher-image when it is attacked by know-plaintext attacks or chosen-plaintext attacks.

(3)    Entropy analysis

Entropy is a scalar value representing the entropy of a greyscale image. It is a statistical measure of randomness that can be used to characterize the texture of the input image. Entropy of an image is defined as:

Е=^ 1 ₌ о Р(х1)1од₂р(х1) (5)

where p contains the histogram counts returned from imhist.

The ideal value of entropy of a cipher-image should be 8. If it is less than this value, there will be some certain predictability that threatens the security.

Table 3 lists the mean entropy values obtained for different original image and the ciphered ones. The obtained results are much closed to the theoretical value. This means that information leakage after 1-round permutation and 2-round diffusion is so tiny that it can be neglected.

T able 3. E ntropy values for different original image and the ciphered ones

Original image

Cipher-image

Entropy of the Originalimage

Entropy of the Cipher-image

7.4767

7.9994

T able 4. 10 groups of NPCR and UACI of the proposed algorithm

NPCR	0.99714	0.99544	0.99828	0.99829	0.99342	0.99809	0.99823	0.99812	0.99306	0.99802
UACI	0.34382	0.33469	0.35326	0.31945	0.33498	0.3532	0.33637	0.34685	0.33266	0.34643

T able 5. 10 groups of NPCR and UACI of different keys

NPCR	0.99586	0.99604	0.99608	0.99607	0.99613	0.99612	0.99613	0.99615	0.99608	0.99607
UACI	0.33447	0.33457	0.33458	0.33446	0.33449	0.33455	0.33453	0.33460	0.33451	0.33453

T able 6. C orrelation coefficients with key Q bkx increased by 1 at different positions

position	left-top (1,1)	right-top (1,50)	left-bottom (50,1)	right-bottom (50,50)	centre (25,1)
Correlation Coefficient	-0.00217286	0.004266592	0.0026746637	-0.000910659	-0.00149085

7.6517

7.3579

7.9992

7.9994

C. Sensitivity-based attack

An algorithm for encrypting an image should be robust enough to resist sensitivity-based attack. This means the cryptosystem should have high key sensitivity and plaintext sensitivity [19]. Further, a tiny change, even a single pixel being modified by one bit, in the key or in the original image, causes a great difference in the cipherimage. These properties make it difficult for diverse sensitivity-based (chosen plaintext, or differential) attacks to break the system.

(1) plain-image sensitivity

The plain-image sensitivity of the cryptosystem is largely infected by the keys that Alice and Bob are holding. Here, two common measures are used to test the system: NPCR (Number of Pixels Change Rate) and UACI (Unified Average Changing Intensity). They are defined as formula (6) [7]:

NPCR =

У. к=1 0 к (pixelValue(ij))

yf . UACI =

H x W IC^i,)) - C24ij)| H x W x 255

x 100%

x 100%

where H and W are the height and the width of encrypted image. D k (pixelValue( i,j )) is determined by the following rule: if the pixel value of C 1 ( i , j )= C 2 ( i , j ) then D(pixelValue(i,j))=0; otherwise D(pixelValue(i,j))=1. NPCR calculates the average intensity of different pixel

numbers between two cipher-images with only one or more pixels changed.

UACI measures the percentage of pixel value differences between the two cipher-images.

Experiments have been carried out on the influence of a one-bit change on a 256 gray-scale Lena image of size 512×512, on the proposed cryptosystem. To get higher accuracy, we divided the experiment into 10 groups, in each of which was arbitrary chosen 1,000 pixels (of different positions, the corresponding pixel value only increased by 1) from the cipher-image.

The values of NPCR and UACI for our algorithm are listed in Table 4.

We can see from Table 4 that the lowest NPCR and UACI is 0.99306 and 0.31945, respectively; the highest NPCR and UACI is 0.99829 and 0.35326, respectively; the average of these two measures’ value is 0.996809 and 0.34071, respectively. While the NPCR and UACI of the proposed, Yang et al.’s cryptosystems is 0.996185 and 0.334795, respectively [9].

Results show that the average performance of the proposed scheme only requires 1-round confusion stage and 2-round diffusion stage to slightly exceed the performance of the scheme introduced by Yang et al. [9], Furthermore, our experiment was tested on the slight change of different pixels and a large number of cases (10×1,000), while Yang et al. tested their system with 1 case. Thus our results are more precise.

(2)    Key sensitivity

The key sensitivity of our proposed scheme benefits from the matrix key K 1 . To evaluate, the key value is increased by 1 at a random position. The results are depicted in Figure 5, which shows that even a difference as small as one value incremented by 1, will result in an incorrectly decrypted image.

(a)

(b)

(c)

Figure 6: Key sensitivity test: (a) cipher-image using the key K 1 , (b) image encrypted with K 1 (c) cipher-image using the left-top value of matrix key increased by 1, (b) image encrypted with K 1 .

It is difficult to compare the cipher-image by merely observing these images. So for comparison, NPCR and UACI are calculated between the two cipher-images using a different key which is increased by 1 at a random position.

For this calculation, we used the same formula given in (4) except that in this test is the values of corresponding pixels in the two cipher-images to be compared. The result is shown in Table 5.

We can see from Table 5 that the average of two cipher-images is 0.996073 and 0.334529, respectively. To get more precise results, another test, which calculates the correlation between the corresponding pixels between the two cipher-images, is implemented. For this calculation, we used the same formula given in (3) except that in this test, it is the values of corresponding pixels in the two cipher-images that are compared in Table 6.

Results show that, for example, the cipher-image by the original key K 1 has 99.78% of difference (this is better than the result from the algorithm proposed by Ismail et al. [20], which was 99.59%) from the one encrypted by the key K₁(1,1) + 1 in terms of pixel grey scale values, although there is only one tiny difference in the two keys.

• V.    Performance evaluation

Apart from security considerations, other issues concerning the image cryptosystem, such as the performance speed, also play a significant role. The performance of an algorithm is affected by many conditions such as: the programmer’s skill; what kind of programme language he is using; the performance of the computer he performs tests on; and how many bits the operation system and the software have.

All the experiments in this paper were carried out with MATLAB programming language as it is strong and readable in the handling of images and matrices. The implementation was done on a personal computer with a 3.20 GHz Core2Duo processor and 2 GB main memory, running with the Windows XP 32-bit operation system.

The encryption procedure consists of three main stages: Calculation of the public key Q b , confusion and diffusion. Table 7 shows the CPU running time when the image was encrypted with the key Q b ^kx in Matlab.

T able 7. T he running time ( ms ) of CPU with the key K 1 in M atlab

k x (of Q b kx )	Confusion stage	Diffusion stage	Calcualtion of Q b kx
1	15.625	242.375	0.022
100	15.625	234.750	15.625
10,000	15.625	242.375	15.625
1000,000	15.625	223.875	31.250
100,000,000	15.625	242.375	46.875
10,000,000,000	15.625	215.625	62.500
1,000,000,000,000	15.625	250.000	62.500

Experiment results indicate that it takes on average 200 to 400 milliseconds for the encryption and decryption stage respectively. It is obvious that the speed of confusion stage and the calculation of the power of Q b is quite fast whilst the diffusion stage consumes a significant amount of time. However, in fact, the diffusion stage is largely the same as that proposed by Yang et al.[9] and Ismail et al. [20]. The reason for the difference is that the use of the bitwise XOR operation results in a longer delay in Matlab than in low level languages. For example, a loop that uses the operation and repeats 512² times takes less than 1 millisecond to complete in C, whereas the same loop in Matlab takes 1.5 seconds.

To compare, we also test in C. Table 8 shows the CPU running time while using C to realize our algorithm.

T able 8. T he running time ( ms ) of CPU with the key K 1 in C

k x (of Q b kx )	Confusion stage	Diffusion stage	Calculation time of Q b kx
1	1.969	2.047	0.0266
100	1.984	2.063	0.0313
10,000	1.969	2.031	0.0312
1000,000	1.953	2.047	0.0328
100,000,000	1.922	2.063	0.0328
10,000,000,000	1.953	2.063	0.0343
1,000,000,000,000	1.954	2.031	0.0360
100,000,000,000,000	1.937	2.047	0.0500
25650-1	1.945	2.041	1787.6

Table 8 shows the running time of confusion and diffusion is quite stable (it is 1.9 to 2.0 milliseconds and 2.0 to 2.1 milliseconds, respectively). The running time of the power of a 50×50 matrix is even much faster than that of confusion and diffusion. Even the matrix Qb to the power of 25650-1, which we thought will consume much time, only takes 1.7876 seconds.

Therefore, compared to the algorithms proposed by Yang and Ismail in 2010, according to the performance evaluation, the sensitivity and statistical analysis, our proposed algorithm is more suitable for higher security purposes and is also suitable for network transmission.

• VI.    Conclusion and future work

  A hybrid-key based image encryption and authentication scheme is proposed in this paper. Ergodic matrix, which is almost uniformly distributed, plays a central role in the encryption/decryption process. It is demonstrated that an ergodic matrix Q eF^ can be employed to completely shuffle and diffuse the original image and has an immense key space of at least3.08×10⁵⁸⁹⁸. With this key space, the scheme is robust enough for the cryptosystem to resist the bruteforce attack. Normally, 1-round diffusion and 1-round permutation is enough for the encryption, but it is vulnerable to differential attack, which, however, is ineffective if a tiny change in the original image (or session key) will cause a great difference in the cipherimage. As a result of this, we have applied one more round of diffusion. It is shown that, in the 2-round diffusion and 1-round permutation scheme, either a single pixel is modified by only one bit in the original image, or only one element of the session key is increased by 1, a significant difference will occur in the cipher-image.

Compared with the existing chaotic cryptosystems [3-9, 15, 16, 19], the experimental tests conducted in this paper demonstrate more optimistic results: the change rate in the number of pixels and unified average changing intensity are both higher, whilst the correlation coefficient is lower.

We can see from Table 8 that the diffusion stage consumes much of the encryption time. How can we achieve a better trade-off between the computing complexity and the security? Is any way that the diffusion stage can be reduced to one round? These are the issues we shall concern ourselves with in our future work.