Erratum: dynamic analysis of optical cell trapping in the ray optics regime

The authors have made a conclusion that the equation (8) from the original paper [1] is not applicable to the considered conditions of microsphere movement after new numerical simulations of trapping dynamics and according to results from the papers [2, 3] and the book [4]. In order to make use of the equation (8) in further calculations, the elementary integration time step the order of 10–9 s has to be considered.

The aforementioned equation (8) was previously used in calculations, because it was not clear for us what parameter was major in determination of microsphere trapping or absence of it (during movement of microsphere in symmetric potential Q Y (S) it moves with positive acceleration in the first half and with negative acceleration in the second half).

Thus, the applicable equation for the numerical simulation of microsphere movement must contain the left part with mass equaling to zero (the zero mass oscillator approximation [4]):

Fy (5 ) + y( Vo - V (5 )) = 0, (1)

In this equation, acceleration is also not considered, because mass is equal to zero. Therefore, a velocity of a microsphere is dependent on the distance S the same way as trapping force and related to it geometrical parameter Q Y (S) . Moreover, the equation (1) is not strongly dependent on choosing the appropriate order of the time integration step.

The condition of trapping is also needed to be changed to the same condition of microsphere escaping from an optical trap:

V max = F y max / Y (2)

The maximal speed for trapping to be performed is proportional to the power of focused laser beam. The table from original paper must be corrected in this way (for microsphere with n S = 1.57) :

Table. Values of maximum speeds

The phase trajectories from Fig.3a-d from the original paper must be replaced with the movement trajectories (Fig. 1 a – b as examples), where calculations are based on the equation (1). Radius of microsphere is considered

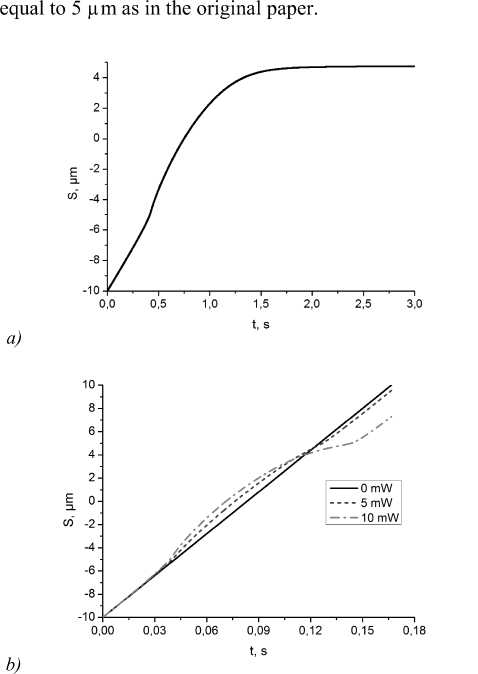
Fig. 1. Trajectories of flowing microspheres with n s = 1.57 under different conditions: a – is a trajectory of trapped microsphere in water flow at the value of the incident power 1 mW; b – is the dynamics of changing the microsphere on flowing in blood plasma at different values of the incident power and at the value of the original speed equaled to 120 µm/s

The trajectory of trapped microsphere is showed on Fig. 1a. The starting velocity is 11 µm/s. The microsphere remains on the equilibrium position – near to the maximum of returning force of the optical trap. The maximum of returning force is obtained when the distance between focus and microsphere center is approximately equal to radius of microsphere. This equality appears due to the consideration of one dimensional force dependence [5].

On the Fig. 1 b , the transformation from the linear to curved trajectory is showed dependent on the laser power value.

Thus, the conclusions of original paper regarding the conditions of microsphere (as a cell model) trapping must be corrected, where numerical simulations based on equations (1) and (2) are considered. The main mismatch between the conditions of trapping is the question of proportionality between maximal critical velocity and power of focused laser beam. However, the trap stiffness calibration can be performed based on the analysis of trapping dynamics [6].