Error prone transmission system to resist data loss in a wireless sensor network

Published Online November 2017 in MECS

According to Cui et al. (2016)[6], in wireless sensor network, during transmission of data, the transmitted data can be erroneous due to several reasons such as limitations of transmission channels, security attacks, channel noises and high complexities of the transmission system in terms of time and space. The transmitted data bits get corrupted due to these reasons in discrete or continuous form. These errors are sometime very large in size. Generally, data link layer is responsible for controlling various transmission errors. However, when the errors are discrete in nature and large in number then the data link layer cannot control such errors. Henceforth, special care is needed to handle the large and discrete data errors at the application layer. Error detection is one of the important aspects for controlling data errors. A number of techniques have been used so far to detect such types of data errors. The parity coding and checksums are the most popular error detecting techniques. However, these techniques cannot detect more than one bit error. Among the various error control codes, use of Hamming code and Hash function can detect position of error bits; however they have distinct limitations too. Hamming code can detect only single-bit error whereas Hash function can detect maximum eight bits of discrete or continuous bit errors (Udgata et al. (2011)[7]. However, among the current error control techniques, no one can detect more than eight bit errors in WSN environment (Miyaji et al. (2011)[8], Liu et al. (2013)[9] and Asaduzzaman et al. (2015)[10]).

As data overhead for tiny devices in WSN is one of the biggest challenges. However, the existing error control techniques are not capable of addressing more than eight bit errors during the communication process. Mostly the repetitive transmission of error control codes are used to address the distinct large size of transmission errors. However, these techniques are imposing a huge data overhead during the transmission process which is not affordable for the tiny communicating devices used in WSN infrastructure. Therefore, to address each individual error bit, we have designed an error control technique which imposes minimal amount of data overhead. Thus, the proposed technique solves the requirement of tiny communicating devices, used in wireless sensor network (Ferng et al. (2014)[2], Nisar et al. (2008)[11] and Berger et al. (2016)[12]). Apart from that it minimizes data loss and offers time efficiency as compared to existing error control techniques. It can detect and correct any numbers of error bits whether they are discrete or continuous which is the primary strength of the proposed error control technique. Apart from that the proposed technique is capable of regenerating original message if data loss occurs due to any unforeseen circumstances. Thus, the proposed technique offers a backup system for accidental data loss during the communication process. The particular objective of this research is to facilitate WSN with,

• •    To minimize transmission errors during the message communication with minimal data overhead.

• •    To reduce data loss caused by various transmission errors and offering a backup system for unintentional data loss.

• •    To provide less time complexity by offering higher processing speed during the execution of proposed technique.

Rest of the paper is arranged as follows: Section II comprises related works to examine research gap by analyzing the strengths and weaknesses of various existing security techniques, Section III displays the detail description about the proposed technique and its functionality, Section IV includes assessment platform to define some important parameters for justifying performances of proposed technique, Section V includes result section to examine performances of the proposed technique in distinct aspects, Section VI contains the conclusions to analyze the strengths and weaknesses of the proposed technique and also proposes a future work for improving its performance.

• II.    Related Works

  Number of efforts has been made to resolve various current issues regarding the transmission errors in wireless sensor network. Among such efforts, few are used to detect and correct distinct transmission errors whereas few are used either for detecting or correcting such errors. Arvaree et al. (2011)[13], proposed an application to verify the competence of error control codes. According to authors, the matter and issues related to competence of an error control code can be covered by software metrics. This research defines how software metrics can be applied for examining competence of the established code in the initial phase of expansion. In this work, a tool was assigned for activating an assumed code. It examines the productivity level and generates productivity information. However, this code is not usable for the external codes. Apart from it, compiler is application specific; henceforth, it cannot be executed in any other environment (Lim et al. (2010)[14], Csoka et al. (2015)[15], Al-Riyami et al. (2016)[16] and Kaur et al. [26]).

Macian et al. (2012)[17] and Ibrahim et al. [27], proposed a method to exploit the probability of sensing corresponding errors using Hamming codes. By selectively employing bits in memory, clear result is attained such that errors corresponding to it produce a disorder that does not match any of those that are adjacent to a single error. This work is verified and applied with diverse nature of input file such as structured or unstructured. However, this method is not suitable for detecting and correcting a large number of discrete or continuous data errors. On the other hand, this technique is not suitable for the tiny devices as it has high time complexity.

According to Cui et al. (2014)[18], Mittal et al. [28], Mancheno et al. (2015)[3], Jamalabdollahi et al. (2016)[19] and Yussoff et al. [29], due to space usage, change in state of an element inside a device or system or single-event upset (SEU) is one of the significant reason of disaster or even fault of system-on chip (SOC), errordetection and correction (EDAC) method frequently accepted to defend memory lockups in SOC contrary to error of SEU. In this work, grouping Hamming code algorithm is applied which uses about 32-bit input data and enhances the capability of EDAC as well as it reduces the region overhead of storing check-bits. Here, every 32-bit data is separated into two groups; each of the groupings embraces a distinct error correction and double error detection (SEC-DED) by using Hamming codes. However, this work requires high amount of execution time to process 32-bits data which makes it unusable for small devices. Apart from that, during the execution, devices consumes huge amount of power which makes it unusable for low-life battery enabled devices.

Wells et al. (2010)[20], proposed a soft error resistant video encoder design which customs the intrinsic construction of current video encoders as a basis for construction of a checksum based error detection appliance. The proposed technique can investigate handling of video frames in parallel with negligible extra price. It can importantly recover superiority of coded video in occurrence of lenient errors. However, retrieval process of original video frames from the encoded video frames suffers with the conversion error. So, the proposed technique is not capable of removing all soft errors from the video frames during communication.

Nisar et al. (2008)[11], proposed small charge codes for sensing called checksum codes and reimbursing of recurrent errors because of voltage over scaling in linear digital filters. According to authors, in the theory of conventional coding, a key issue is analyzing data errors and experiencing important latency as well as computation rates. Hence in this work, latches of low precision shadow have been introduced to classify errors sources because of power over-scaling. The main strength of proposed technique is that it does not require any training and this system acclimatizes energetically to save power, keeping system presentation within satisfactory range. However,in this technique, data errors can be incorporated due to power-fault during the execution of entire process. Apart from that, data loss may also occur due to electrical leakage.

According to Reviriego et al. (2012)[21] and Csoka et al. (2016)[22], single error correction (SEC) code is one of the traditional memory error correction code. Apart from that, further progressive error correction codes (ECC) are normally used when extra protection is necessary. These types of error correction codes should have capabilities to detect the errors as well; however, this feature is normally absent in such kind of error correction codes. Consequently, as per authors, currently available ECCs and SECs are more advanced as they can correct double or triple bits memory errors. Nevertheless, these types of codes offer high execution complexities which liquefy their importance. Henceforth, authors proposed an advanced difference set code to correct as well as to detect distinct errors which are more than single bit along with low complexities. This mutual error detection and correction competency makes the proposed scheme a favorable choice for memory application. However, the proposed technique cannot detect and correct a large number of discrete or continuous error bits. Subsequently, it offers high latency time during the execution which makes it unusable for tiny devices.

Singh et al. (2012)[23], introduced the forward error correction (FEC) code for wireless sensor network. According to authors, lifespan of any wireless sensor network directly relies on effectual usage of its power requirements. Power is mainly used up during wireless communication and reaction. As power maintenance is a key problem of concern in WSN, replication of transmission is not a reliable choice and FEC would be favored over Automatic Repeat Request (ARQ). In this research effort, a well-organized FEC technique for WSNs has been used to escape from retransmission which is not only protects power but also spreads its efficiency and allows it to tackle multi-bit burst error. This error correction technique is efficient for minimizing burst error of even 8-bits. However, this technique is not capable of correcting more than eight bit (discrete or continuous) errors.

Hong et al. (2010)[24], proposed a quick errordetection (QED) technique for actual post silicon authentication for detecting multiple-bit data errors. This technique is mainly introduced for the tiny devices. It converts current post silicon endorsement trials into newfangled authentication checks which expressively decrease error detection latency. QED alterations permit elastic adjustments between attention, error-detection latency and difficulty and can be applied in software with slight or no hardware deviations. However, this technique cannot solve distinct logical bugs during the execution process. This technique is also not effective in the wide range communications.

Henceforth, from so far discussion, we have seen that the present error control techniques are fail to offer any concrete solution for detecting and correcting large data errors with low time and space complexities. These error control techniques need further improvement to enhance their efficiencies. Current literature shows that there is no error control technique available which can detect as well as correct more than eight-bit discrete or continuous errors in WSN environment. Therefore, when a large number of error bits are incorporated within the transmitted data during the communication process, it is very hard or nearly impossible to remove them. Henceforth, in this paper, we have proposed a new error control technique which can detect and correct any number of error bits (whether discrete or continuous).

• III.    Proposed Technique

From the existing literature we have seen that existing error control techniques are not able to resolve a large number of discrete or continuous errors. Henceforth, we have proposed an error correction technique to control any number of discrete or continuous error bits. First subsection provides the description of error control bit generation and incorporation within the original input data and the second sub-section describes the working principle of the proposed error control technique.

• A.    Error Control Bit Generation and Incorporation

The proposed technique involves two rounds of error control-bit incorporation operation.

In the first phase, error control system is included for providing a backup system to avoid accidental data loss. Consequently, second round of error control technique is applied for addressing each and every error bits individually. The overall structure of proposed error control technique is shown in Fig.1. Fig. 1 clearly shows the dual phases of proposed error control bit incorporation technique. The first phase started with splitting input pair of 8-bit binary strings. After splitting, each pairof 8-bit strings are taken and after that lower valued string is subtracted from the higher valued string. These two continuous strings and subtracted string are then concatenated into single string and completed the first phase of error control bit incorporation. In second phase, concatenated sting is taken and performed binary addition of each pair of continuous bits and the resultant bits are placed after each pair of input bits. The proposed algorithm is described by Algorithm-1.

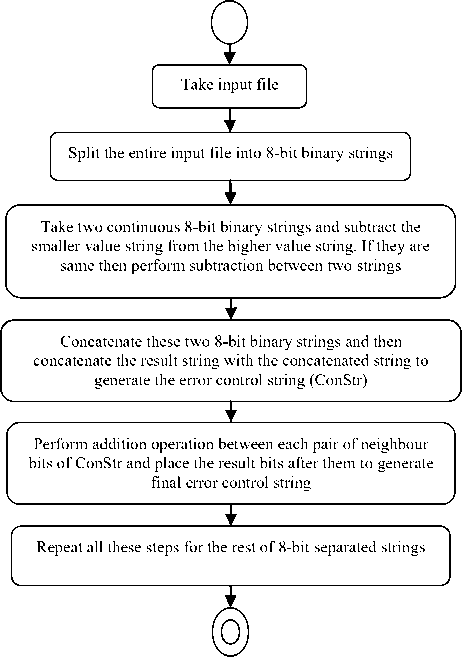
Fig.1. The Proposed Error Control Model

Algorithm-1: Proposed error control bits integration technique

//First phase of error control bit incorporation

• a)    Split the input file into n numbers of small 8-bit binary strings.

• b)    Let the two 8-bit input strings are Strl and Str2 . Calculate the decimal values of Strl, Str2 and store them in numl and num2 as,

numl = ^(Strl, x 2‘), i=o num2 = ^(Str2, x 2‘)

i=o

Here, i is the bit position.

• c)    Perform the subtraction between numl and num2 and store the subtracted values in string variable subl as, if (numl >  num2)

subl = numl — num2

Else subl = num2 — numl

//Conversion of 8-bit string

• d)    Convert subl into binary string as,

x = subl modulo2^l           )

subl

where0 < i < 7

■ ifyl ^ l

= z x (l0) ^i(z) + x, where l(x) = [loy lO J + l

Here x,y1and z are the ordinary integer variables and s' is a string variable where i represents the bit sequences of s'.

• e)    If s is of 8-bit length then put it in the string array sub' as sub' = s'

Else make s' 8-bit by concatenating zero (0) at MSB (Most Significant Bit) position of s ' and put it in the two-dimensional string array sub' as sub = s'.

• f)    Concatenate Strl, Str2 and sub' into ConStr as, ConStr = (Strl x (l0) ⁱ⁽«^r2) + Str2) x l0 ⁱ⁽™^b ' ) + sub'

Where, l(Strl) = ([lo^ f0 ^r1 ] + l), l(Str2) = Qlogf^ ² ] + l) and l(sub') = ([lo^ f^ ^b J + l).

//Second phase of error control bit incorporation

• g)    Perform addition between each pair of consecutive bit of ConStr and incorporate the dual results bit after them as

g1) If xl is any ordinary variable then perform, xl = ConStr , + ConStr_i+1

g2) If the length of xl is 1 -bit then add 0 at MSB (Most Significant Bit) position of xl.

g3) Concatenate ConStr, ConStr', and xl into a single string variable C where initial length of C' is 0,

^C ' = (((((^C ' x^l0)+ ConStr , ) x ю) + ConStr , ₊₁) x Ю0) + xl, Where 0 < i < 8.

• h)    Repeat steps (a-g) for rest of the dual consecutive 8-bit strings and concatenate all of them into a single string.

In Algorithm-1, step (a) splits the entire input file into 8-bit binary strings. After splitting the input file into several small strings, dual consecutive 8-bit strings are taken from the split strings and assigned to string variables Strl and Str2 for initial phase of error control bit incorporation using step (b). Step (b) also calculates the decimal values of Strl and Str2 and store them to numl andnum2 integer variables. Step (c) subtracts num2 from numl when numl is greater than or equal to num2 . Consequently, step (c) subtracts numl from num2 when num2 is greater than numl . The subtracted result is stored into subl by the step (c) too. Steps (d) and (e) convert the subtracted values into 8-bit binary string (s ' ) and put it to a string variable sub'. Step (f) concatenates Strl, Str2 and sub' into a single string and stores the concatenated string into string variable ConStr. Thus, with step (f), first phase of error control bit generation as well as incorporation operations is completed. In second phase, step (g), adds the two consecutive bits of ConStr in the dual bit format to represent sum and carry bits. The sub-step (g1) adds the two each pair of consecutive bits and outcome is stored into variable xl and the sub-step (g2) checks length of.

xi and if it is single bit, then, it adds 0 at the MSB (Most Significant Bit) position. Sub-step (g3) concatenates the resultant binary string xi withConStr to include final error control bits. Step (h) repeats all these steps (a-g) for rest of the 8-bit separated strings wherein with the each iteration; two 8-bit consecutive strings are taken as input

• B.    Workings of the proposed error control technique

After receiving the complete string on the other end, it is used as input to detect and correct the transmission errors. The proposed error control technique is then applied to the received string to detect and correct erroneous bits with referenced error control bits. The vivid working of the proposed error control operation is described by Algorithm-2.

Algorithm-2:  Workings of proposed error control operation

//First round of error control operation a1) Take received string and store it into the string variable StrwherefStr,) represent the bit sequence ofStr. Let AddStr as well as Ori are ordinary string variables and if n is the total length of received string (Str) then perform, for (i = 0; i < n; i + 4)

AddStr = (Str) , + (Str)_i+1

a2)  If AddStr is single bit string, then,

Add 0 at MSB position of AddStr End if a3) Match each bit of AddStr with (Stri+2Stri+3)

a4) If all bits of AddStr matched with (Stri+2Stri+3), then perform

Ori = (((Ori x 10) + Str , ) x io) +Str_i+1, Where,Orl is a string variable and initial length of Ori is 0.

End If a5) If match is not done then generate the original string by performing subtraction between   Str,    and

i+ 2 Str_i+3⁾orStr_i+ i andi+ 2 Str_i+3⁾.

Perform the following operation to eliminate i+ 2 Str_i+ 3 ⁾,

Ori = (((Ori x 10) + Str , ) x io) +Str_i+1

End If

End for

// Second round of error control operation a6) Let the length of Ori ism, where m < n. Take Ori as input and separate each 8-bit string from it and store them into a two-dimensional string array EC.

a7) Perform subtraction between EC j and EC j ₊₁ according to the Algorithm-1 and compare the subtracted result with the EC j ₊₂ where 0 < 7 < (m ^ 8).

a8) If match is done,

Eliminate EC j ₊₂with the help of step (a4) or (a5)

End If a9) If match is not done, replace corrupted bit using ECj+2 and ECj or ECj and ECj+1 by performing, subi = ECj+2 + ECj , sub2 = ECj+2 - ECj , sub3 = ECj - ECj+2

subi' = EC j ₊₁ + EC j , sub2' = EC j ₊₁ - EC j , sub3' = EC_j - EC_j+1

Match among (subi, sub2,... subi ' ,..sub3) and take maximum matched positive result from the list.

Eliminate EC j+2 with help of step (a4) or (a5)

End If a10) Repeat step (a7) to (a9) for the rest of the elements of EC.

a11) After eliminating all error control bits from EC by repeating step (a8) or (a9), reform the output file as same as the input file format.

In Algorithm-2, step (a1) declares some string variables for presenting the proposed error control algorithm. Step (a1) also stores the entire received string into the string variable Str and adds each pair of consecutive bits of Str into another string variable AddStr. Step (a2) checks the length of AddStr and if the length of AddStr is single bit then this step adds a 0 at the MSB position of AddStr . Step (a3) compares AddStr with the combination of next two bits ofStr which are the error control dual reference bits. If match is done then step (a4) eliminates the extra error control reference bits and stores the original bits in a string variable Ori where the initial length of Ori is 0. If the match is not done, step (a5) detects the corrupted bit with the help of referenced error control bit and replaced the corrupted bit by regenerating the original bit. Step (a5) eliminates the dual reference error control bits after correcting the erroneous bit. Step (a5) further puts the original bits into the string variable Ori after eliminating dual reference error control bits. Steps (a1-a5) are repeated for other bits of received strings (Str)to correct all individual bit errors and for eliminating referenced error control bits. With the elimination of referenced error control bits, first round of error control operation is accomplished.

In the second round of operation, newly generated string Ori is taken as input where the length of Ori is m. Step (a6) separates (m/8) numbers of 8-bit strings from m and stores them in two-dimensional string array EC. Step (a7) subtracts each of the two consecutive elements (i.e. 8-bit strings) of string array EC . The subtracted string is then compared with the next 8-bit string EC which is a reference 8-bit error control string. If the match is done, step (a8) eliminates the reference error control string. If match is not done then, step (a9) modify the corrupted string with the help of reference error control string and after removing all errors, step (a9) eliminates the reference error control string from the EC. Step (a10) repeats the steps (a7-a9) for the rest elements of EC . After eliminating all the reference error control string, retrieved original strings are concatenated and forms the output file in the same format of input file using step (a11). Thus, the original file is retrieved at the receiving end after performing the proposed error control operation to remove any number of discrete or continuous error bits.

• IV.    Assesment Platform

This section basically includes the description of experimental setup, data preparation for our experiment and few important parameters which will be used during the result analysis in the next section to justify the performances in distinct aspects and to justify our objectives.

• A.    Experimental Setup and Data Preparation

The implementation and the performance testing of the proposed error control technique have been done in the Linux environment. Java is used as programming language during the implementation of proposed error control technique. The wpa_suppliment software tool (provided by the Linux) and DHCP client component is used for testing the performance of proposed error control technique in WSN environment. We have tested with distinct kind of input files which are suitable for tiny or small devices that are mostly used in WSN. We have tested with the text data, image and video files to maintain the diversity of input files.

• B.    Some Important Definition

During result analysis, performances of proposed error control technique in different aspects are represented with the help of few parameters. Henceforth, this section defines these parameters to justify their relationship with the proposed technique.

• 1)    Signal to Noise Ratio (SNR_dB)

Signal to noise ratio is the sample length of digital data relative to number of incorporated errors. It can be expressed logarithmically in decibels (dB). If SNR of any sample is high, it signifies that the sample is less erroneous. In the equation (1), x(n) is the length of input samples, whereas y(n) is the length of output sample. It can be formulated by using equation 1,

SNRdB = 10 X Log^^^*^^ (1)

• 2)    Information Loss (IL)

Fewer, during the transmission, some portions of transmitted information are modified or corrupted by the channel noise or some unwanted circumstancessuch as interference of illicit third party, limitations of transportation system. Mostly this information cannot be retrieved at the receiver end, i.e., it gets permanently lost. Such phenomena are known as information loss ( IL ). It can be formulated by using equation 2,

IL =

Actual file Size-Retrieved, file size ^ ^QQ

Actual File size

Any data transmission system is considered highly secure and robust when the information loss occurred during the transportation is very small. In our proposed model, information loss is calculated for justifying the effectiveness of proposed scheme against data errors and various security attacks.

• 3)    Throughput (TP):

Throughput or TP is the amount of work done in a given time. It is measured to calculate the time efficiency of a certain technique. The throughput produced by any technique can be calculated by using equation 3,

TP

( Output file size \ Total execution time /

As we know that, time requirement is inversely proportional to the processing speed of a computing system i.e. with the increment of processing speed, time requirement to accomplish a job decreases. So in these circumstances throughput is increased with the increment of processing speed.

• 4)    Cyclomatic Complexity (CC):

Cyclomatic Complexity (CC) is a measure of source code complexity that has been correlated to the number of coding errors. It is calculated by producing a control flow graph (CFG) of the code that is used to find the number of linearly-independent paths throughout a program unit. The Cyclomatic Complexity of any technique or algorithm can be determined by equation (4). In equation(4), M denotes the Cyclomatic Complexity of any technique, E denotes number of edges, N is the number of vertices or nodes, and P is number of predicate nodes (node that contains condition) of control flow graph.

M = (E-M+ (2 XP)) (4)

If CC of any technique is high, it is considered as highly time complex ((Mieee B. Nkom et al. (2011)[25]. A range of Cyclomatic complexities and their corresponding analysis are given in Table 1.

Table 1. Cyclomatic Complexity Range

Cyclomatic Complexity	Evolution
1-10	Simple, low risk and highly capable
11-20	Complex, risk and reasonable efficiency
21-50	Highly Complex, risk and less efficiency
> 50	Unstable, inefficient and unreliable

• V. Result Analysis and Discussion

In this section, we will test the performance of our proposed technique to minimize data loss and its time efficiency. According to the assessment platform section, capacity of data loss can be justified by analyzing the SNR value produced by the output file after applying any error control technique. The capacity of minimizing data loss can be further analyzed by calculating percentage of Information Loss (IL). SNR and percentage of Information Loss produced at the receiving end after applying proposed dual round of error control operations and some current corresponding techniques have been calculated with the help of Equation (1) and Equation (2). The results of these tests have been plotted in Fig. 2 to compare the performances of proposed error control technique in the context of minimizing transmission errors. From the assessment platform section, it can be seen that SNR is one of the important parameter which can examine the efficiencies of any error control technique to remove the data errors after applying it. As per the definition, if any error control technique offers higher SNR then the used error correction technique is said to be efficient to remove data errors. Henceforth, to justify the performances of the proposed error correction technique in terms of its capacity of removing errors has been calculated and compared with corresponding error control techniques with respect to SNR in the following Fig. 2.

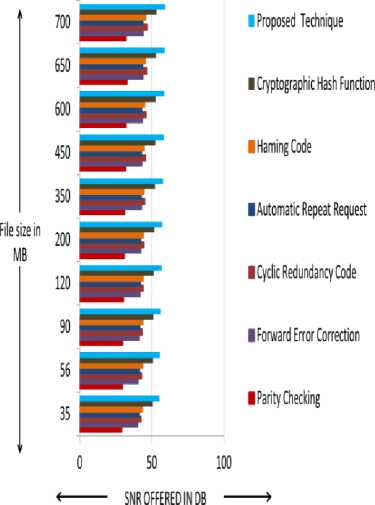
Fig.2. SNR Produced by Applying Distinct Error Control Techniques

As the proposed technique can address each and every error bits and remove them efficiently after detection. Henceforth, Fig. 2 shows that the proposed error control technique produces better SNR after removing maximum numbers of transmission errors than the other corresponding error control techniques. According to definition of assessment platform section, if any error control technique offers higher SNR , then the applied error control technique is said to be efficient to minimize the bit errors. Henceforth, according to the definition, our proposed error control technique is more efficient to minimize data errors, caused by dusting transmission limitations than other correspondents. The efficiencies of the proposed error control technique and other existing error control techniques for minimizing data loss as well as data errors are further investigated in terms of percentage of Information Loss ( IL ) and plotted in the following Fig. 3.

In Fig. 3, we have compared the efficiency of proposed technique to reduce data loss during the transmission process with few well known existing error control techniques.

From the definition of assessment platform section, it can be seen that if the percentage of Information Loss (IL) is low after applying any error control technique then the applied technique is considered as efficient to protect data loss during the transmission. Henceforth, from the Fig. 3, it can be seen that proposed error control technique offers minimum percentage of Information Loss (IL) rather than the other existing techniques. Henceforth, the proposed error control technique is efficient to protect data loss among the rest techniques.

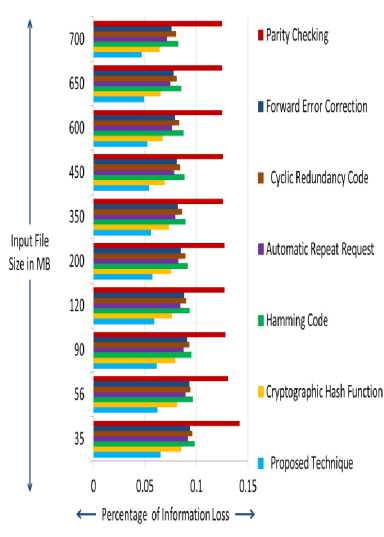
Fig.3. Percentage of Information Loss Offered by Distinct Error Control Techniques

Therefore, from Fig. 2 and Fig. 3, we can see that the proposed technique is efficient to reduce the distinct transmission errors and data loss during the transmission rather than the other existing error control techniques as proposed error control technique can address each and every error bits whether they are discrete or continuous. Even proposed error control technique can control any number of errors during its dual rounds of error control operations. Fig. 2 and Fig. 3 also show that Parity Checking offer very poor performance in controlling distinct transmission errors as well as the data loss during the data transmission in wireless sensor network environment. Henceforth, we will not further compare the performances of Parity Checking with our proposed error control technique in our discussion.

Another important aspect in wireless sensor network for secure data transmission is processing time. If any error control technique takes higher time during generation, incorporation of error control bits or during the detecting as well as correcting error at the receiving end, it may cause data loss. Henceforth, from the definition of assessment platform section, we have compared the time efficiency offered by the proposed technique with other existing techniques in terms of their capacities to offer Throughput with the help of Equation

• (3) . The results of such calculation and comparison have been plotted in Table 2.

Table 2. Throughputs Offered by Distinct Error Control Techniques

Error control techniques for data bits	Generation and Incorporation (MB/Sec)	Detection and/or Correction (MB/Sec)
Forward Error Correction	1.59	1.57
Cyclic Redundancy Code	1.24	1.22
Automatic Repeat Request	1.21	1.20
Hamming Code	1.21	1.23
Cryptographic Hash Function	0.91	0.93
Proposed Technique	1.75	1.73

The proposed error control technique performs both error control bit generation and incorporation at the sending end and dual round of error control operations at the receiving end in single iteration. Henceforth, it involves low time requirements rather than the other corresponding error control techniques. Therefore, the proposed error control technique offers higher Throughputs for both generating as well as incorporating error control bits at the sending end and error control operation at the receiving end. In Table 2, we can see that the proposed technique offers higher Throughput than the other existing techniques. Henceforth, according to the definition, data processing speed of the proposed error control technique is faster than the other existing techniques.Table 2 also shows that Cryptographic hash function offer lower time efficiency than others though it offers better result in controlling bit errors and protecting data loss during transmission (refer Fig. 2 and Fig. 3). The complexity of the proposed and other existing error control techniques have been further investigated by calculating the Cyclomatic Complexity with the help of equation (4). The results of such calculations have been plotted in the Table 3.

Table 3. Cyclomatic Complexities of Distinct Error Control Techniques

Error control techniques for data bits	Cyclomatic Complexities during generation and incorporation of error control bits	Cyclomatic Complexities during detection and correction of bit errors
Forward Error Correction	4	3
Cyclic Redundancy Code	4	3
Automatic Repeat Request	4	3
Hamming Code	3	3
Cryptographic Hash Function	4	4
Proposed Technique	2	2

In Table 3, we can see that proposed technique offers lowest Cyclomatic Complexity among the rest techniques. The proposed error control technique involves only dual rounds during both generation and incorporation of error control bits as well as during detection and correction of error control bits. On the other hand, the existing repetitive code transmission processes like cyclic redundancy code, forward error correction and automatic repeat request uses multiple iterations to replace all error bits during their execution. Consequently, Hamming code technique can only detect and correct single bit with in the eight bits. Hence, it requires large time to detect and correct large number of errors during its execution. In the Cryptographic hash function, complex encrypted text as well as hash values are generated during the execution in both error control bit generation as well as detection and correction process. Hence, cryptographic hash function involves high execution time and complexity. Conversely, Table 3 also justifies that proposed technique offers low execution complexity rather than other existing error control techniques. Hence, according to the definition, it is time and space efficient.

Henceforth, Fig. 2 and Fig. 3 show that the proposed technique is efficient to reduce transmission errors and data loss during the transmission process which satisfies our first and second objective. Consequently, Table 2 and Table 3 shows that our proposed technique offers better time and space efficiencies rather than the other existing error control techniques which satisfy our third objective as well.

• VI. Conclusions and Future Work

  Transmission errors are a big issue for any data communication system. In wireless sensor network, data loss may occur and data errors can be incorporated for diverse limitations of transmission system. Generally, these kinds of incorporated bits errors are multiple bits or single bit and incorporated in continuous or discrete form within the transmitted data. Mostly data link layer is responsible for controlling distinct error during the transmission process (Hong et al. (2010)[24] and Mancheno et al. (2015)[3]). In these layers, a number of error controls have been deployed. On the other hand, over the time of period, distinct error control techniques have been applied on the application layer too. However, these techniques are not capable of controlling large number of data errors whether they are discrete or continuous. Few of them can only detect the single bit error. The existing literature review shows that among distinct existing techniques, only cryptographic hash function can only detect as well as correct 8-bit discrete or continuous errors. Henceforth, to address as well as control any number of bit errors whether they are discrete or continuous, we have proposed an error control technique for wireless sensor network. The proposed error control technique involves dual round operations to control each individual error bit. Apart from it, the proposed technique offers a backup system for an accidental data loss. Result analysis section also justify that proposed technique is efficient to reduce data errors as well as data loss rather than other existing techniques. Result analysis also shows that proposed technique is time and space efficient rather than other correspondent. Thus, the dual objectives of this research work have been achieved.

However, the proposed error control technique cannot control complete data loss. Henceforth, there is further future scope to improve it. Apart from it, time efficiency of the proposed technique can be improved by enhancing processing speed. Therefore, upgrading of processing speed and reducing the data loss are the future scope of this research.