Estimation of Noise in Nonstationary Signals Using Derivative of NLMS Algorithm

Published Online August 2017 in MECS DOI: 10.5815/ijigsp.2017.08.02

The signals can be classified into stationary and nonstationary signals. The processing of stationary signal is easy because their statistical parameters like the amplitude distribution and standard deviation would be same with time. But processing of nonstationary signals is very difficult because their statistical parameters are changes with time. The best examples for nonstationary signals are speech and Electroencephalogram (EEG).

Speech is the important way of communication in human being. In the modern world it is necessary to transmit the speech from one part to other through succession of process using communication channels. At the receiving end, most of the times the speech signals are corrupted by some form of the noise components resulting in reduced quality and intelligibility of speech signal. So the original speech becomes unpleasant to listen. The amount of unpleasant is depending upon the type of noise corrupted to the speech signal. The noise will be either stationary or nonstationary in nature. The quality and intelligibility of the speech in the presence of background noise can be improved by speech enhancement algorithms. Over many decades researchers are focused in this area and developed the different algorithms to remove the noise which is present along with the speech signal. The enhancement of signal in noisy environment is very important and still active field of research [4-9]. The noise added with speech signal is stationary in nature then, it can be easily suppress using spectral subtraction and wiener filter [11-13]. But if it is nonstatinary in nature then it is very difficult to suppress.

The bioelectric signal available from human being is very important for diagnostic and therapeutic purpose. The important bioelectric signals are Electrocardiogram (ECG), Electroencephalogram (EEG), Electromyogram (EMG), and Electrooculogram (EOG) and so on. The nature of bioelectric signals is weak so while recording, it has more affinity to attract the surrounding noise. Electroencephalogram (EEG) [10] is the study of electrical activity of the brain which represents graphical recording of electrical activity of large number of neurons and synapses. While recording EEG the different stationary and nonstationary noises are added, such as external noise like AC power lines, surrounding electrical equipments and physiological noises like electrooculogram (EOG) and electromyogram (EMG) [19].

Many researchers are focusing to  suppress  the background noise and enhance the original signal. The adaptive filter is still better tool to suppress the background noise and estimate the original signal in noisy environment for both speech and bioelectric signals [21]. Researchers are worked on different forms of adaptive filter like least mean square (LMS), Leaky LMS, NLMS and Recursive least square (RLS) algorithm for speech enhancement [25], removal of noise in EEG and extraction of fetal ECG from maternal ECG [20]. In the basic adaptive filter like least mean square (LMS) algorithm the step size remains constant in weight equation for all the input samples. [2]. The basic block diagram of adaptive noise canceller is shown in Fig1. Primary input d(n) consists of the sum of desired signal

s(n) and uncorrelated noise n 0 (n). The noise n 0 (n) is uncorrelated with s(n). The reference input x(n) is another noise n 1 (n ) which is correlated with n 0 (n) and uncorrelated with s(n).

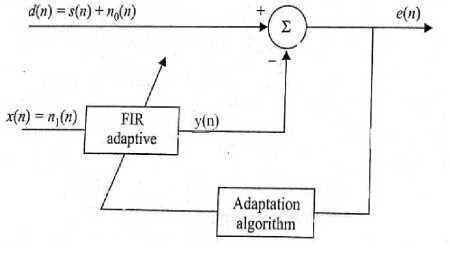
Fig.1. Adaptive noise canceller

^w( n+l ⁾ = ^w(n)+     2 ^-—      ^{x(n)e(n )  (4)}

tz||eL(n)|| T(1-a)||x(n)||2

Where eL(n)ll2=Z— |e(n - Q|2         (5)

The parameter ‘L’ represents fixed number of samples selected on the basis to get optimum response.

The proposed algorithm may be considered as modified EDNSS algorithm in which replacing the error vector for fixed samples ‘L’ to total samples ‘n’ for better stability,

Then the denominator term becomes

||eL⁽n)|| ² = | |e⁽^⁾|| 2

Where

• II.    Proposed Algorithm

The normalized LMS (NLMS) algorithm overcomes the fixed step size problem and step size varies from one iteration to the next, the weight vector of an adaptive filter change along with the input. The rate of convergence of NLMS algorithm is faster than that of LMS filter [1].

So the method of varying the step size is focused by many researchers and developed different forms of NLMS algorithms [14-18]. In which EDNSS algorithm is also one among them. The proposed algorithm is modification of EDNSS algorithm and has fast convergence compare to EDNSS, which is required feature for speech and EEG. Which is clearly shows improvement in terms of decreasing EMSE and misadjustment. The proposed algorithm

The output, error and weight equation of conventional NLMS algorithms are shown below.

The output;

y(n)=w(n).xT (n)(1)

The error;

e(n)=d(n)-y(n)(2)

The weight equation:

w (n+l) =w (n) +   -   x(n) e(n)(3)

T ||A(M)| |

Where w is the adaptive filter vector weight and ||x(n)|| ² is equal to x(n)*x^T(n), const (e) is used in the denominator to prevent the division by a very small number.

A modified form on NLMS algorithm introduced in called as Error-data normalized step-size (EDNSS) [3] algorithm and the weight update equation is given by lle (n)ll2='L'n— |e(n - i)|2            (6)

The parameter ‘n ‘represents the total number of speech samples.

Then, (4) can be rewritten as

^w(n+1) = ^w(n)+-      2^_f^-  ... ₍ ^x ( ^x(n)e(n )

a||e(n)|| T(1-a)||z(n)||2

The performance of the adaptive noise canceller may be described in terms of the excess means square error (EMSE) [22-24] and misadjustment ‘M’ [3-8]. The EMSE at the n ^th iteration is defined by

EMSE (n) = 1 £^ о¹ |е1(п-/)| ² (8)

Where e1(n)=e(n)-s(n ) is the excess residual error. The steady state excess mean square error (EMSEss) is defined by

EMSE ss — Z K-P EMSE (n)        (9)

K-P

Where K is the total number of samples of the speech signal and P is the number of samples after which the algorithm reaches steady state.

The misadjustment is given by

EMSEss

M=---

MSEmin

Where

MSE min=- 1- Z £₌p |s(n)| ²         (11)

K-P

The simulations are carried with speech signal and EEG. The speech signal “sp23” IEEE standard data base of male voice saying” stop whistling and watch the boys march” The original signal has 21209 samples and the raw EEG signal contains 71200 samples. The simulations are carried with K=21209 for speech signal and 71200 for EEG, N=10(length of the filter), L=200 P=1, α=0.7 andµ=0.1.

A. Stationary noise

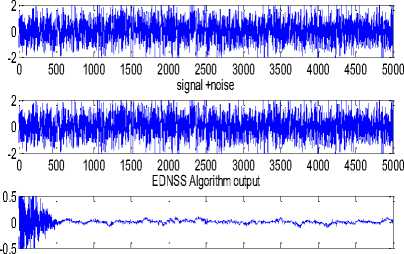
The performance of this algorithm is computed by adding the white Gaussian noise of zero mean and with three different variance levels at 0.1, 0.5 and 0.7. Fig 2 illustrates the performance of EDNSS algorithm for stationary noise corrupting the speech signal with variance ( σ ² ) of 0.5. From top to bottom that Fig shows input signal, noise, signal+noise, output and minimum mean square error. The same for proposed algorithm is shown in Fig 3. The comparison of EMSE variations for speeh signal in dB for both the algorithms is shown in Fig 4. Fig 5 & Fig 6 demonstrate the performance of the EDNSS and modified algorithm for EEG signal and which is plotted for 5000 samples to illustrate the robust convergence. These Figures clearly demonstrate that the rate of convergence of proposed algorithm is faster compare to EDNSS algorithm. EDNSS algorithm adopts approximately after 500 samples but same in the proposed algorithm is 150 samples. The comparison of EMSE variations for EEG signal in dB for both the algorithms is shown in Fig7.The simulated result in terms of steady state excessive mean square error and misadjustment for speech signal and EEG are shown in Table 1 and Table 2 respectively. Which is clearly demonstrates that the EMSEss decreases in proposed algorithm compared with EDNSS for different noise levels and also proposed algorithm maintains almost constant EMSEss for increasing variance level in the noise.

x 104

input Noise

2 0

-20               0.5               1               1.5               2               2.5

4 x 10⁴

signal +noise

-20               0.5               1               1.5               2               2.5

x 104

Proposed Algorithm output

Fig.3. From top to bottom, the original speech, the noise, signal+noise, noise cancelled speech and excessive mean square of proposed algorithm for stationary noise

2 0 -20

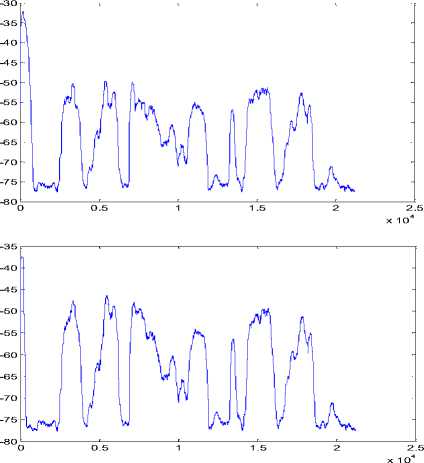
Fig.4. Top to bottom, excessive mean square error of EDNSS and proposed algorithm in dB for stationary noise (Speech signal )

x 104 input Noise

1               1.5               2              2.5

x 104 signal +noise

0 М               МММi

-2

0.5

0               0.5               1               1.5               2              2.5

x 104

EDNSS Algorithm output

-0.50 1^^^^^^^^^^^^^ . 0                 0.5                 1                 1.5                 2                 2.5

x 104

x 10-5                        Mean Square error

x 104

Fig.2. From top to bottom, the original speech, the noise, signal+noise, noise cancelled speech and excessive mean square error of EDNSS algorithm for stationary noise

0.5

Input signal

-0.5 :------------------:------------------[-----------------[------------------:-----------------,------------------[-----------------[------------------,-----------------,------------------1

0    500   1000  1500  2000  2500  3000  3500  4000  4500  5000

input Noise

■ x 10-

500   1000  1500  2000  2500  3000  3500  4000  4500  5000

-4                          Mean Square error

-30

-35

-40

-45

-50

-55

-60

-65

-70

-75

x 10

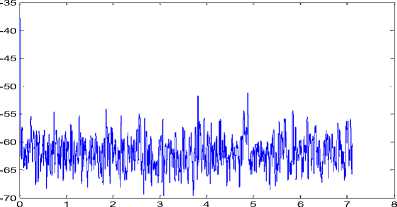
Fig.7. Top to bottom, excessive mean square error of EDNSS and proposed algorithm in dB for stationary noise (EEG Signal)

0:--------------<-----------1--------------1--------------:--------------1--------------1--------------1--------------1--------------1--------------1

0    500   1000  1500  2000  2500  3000  3500  4000  4500  5000

0.5

Fig.5. From top to bottom, the o riginal speech, the noise, signal+noise, noise cancelled EEG and excessive mean square of EDNSS algorithm for stationary noise

Input signal

0    500   1000  1500  2000  2500  3000  3500  4000  4500  5000

input Noise

-0.5

-

-2

ш11ЙШЙ^и^

0    500   1000  1500  2000  2500  3000  3500  4000  4500  5000

signal +noise

-2

Щш|Ы

0.5

0    500   1000  1500  2000  2500  3000  3500  4000  4500  5000

Proposed Algorithm output

1² b

0 L3^--------:-------:--------1-------1--------1-------1--------‘-------1-------J

0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000

. 0     500   1000   1500   2000  2500   3000  3500  4000  4500   5000

_{x 10}^-4                         Mean Square error

-0.5

Fig.6. From top to bottom, the original speech, the noise, signal+noise, noise cancelled EEG and excessive mean square of proposed algorithm for stationary noise

B. NonStationary noise

For nonstationary case noise is assumed as white Gaussian noise with zero mean with a variance that linearly increases from minimum of 0.0005 with different maximum variance levels at 0.0055, 0.0505, and 0.5005 and 0.5555.

Fig 8 illustrates the performance of EDNSS algorithm for nonstationary noise corrupting the speech signal with σ ² min=0.0005 & σ ² max=0.5005. From top to bottom that Fig shows the input signal, noise, signal+noise, output and minimum mean square error. The same for proposed algorithm is shown in Fig 9. The comparison of EMSE variations for speech signal in dB for both the algorithms is shown in Fig10. Fig11&Fig12 demonstrate the performance of the EDNSS and modified algorithm for EEG signal and which is plotted for 5000 samples to illustrate the robust convergence. The comparison of EMSE variations for EEG signal in dB for both the algorithms is shown in Fig13. These Figures clearly demonstrate that the rate of convergence of proposed algorithm is faster compare to EDNSS algorithm. EDNSS algorithm adopts approximately after 500 samples but same in the proposed algorithm is 150 samples.

The simulated result in terms of steady state excessive mean square error and misadjustment for speech signal and EEG are shown in Table 2 and Table 4 respectively. Similar to stationary noise the EMSEss decreases in proposed algorithm compared with EDNSS for different noise levels and also proposed algorithm maintains almost constant EMSEss for increasing variance level in the noise.

x 104 input Noise

-2

0                0.5                1                1.5                2                2.5

x 104

signal +noise

-20                0.5                1                1.5                2                2.5

x 104

EDNSS Algorithm output

x 104

x 10-5

Mean Square error

x 104

Fig.8. From top to bottom, the original speech, the noise, signal+noise, noise cancelled speech and excessive mean square of EDNSS algorithm for nonstationary noise ( σ ²max=0.5005)

Fig.10. Top to bottom, excessive mean square error of EDNSS and proposed algorithm in dB for nonstationary noise (Speech signal)

Input signal

0.5 :                  " г                            [                            г                            [r

0 --4н-#Н»е--^^

-0.5 ---------------------1---------------------1--------------------Z-------------------[1

0                0.5                1                1.5                22.5

0.5

Input signal

0    500   1000  1500  2000  2500  3000  3500  4000  4500  5000

input Noise

-0.5

x 10 ⁴

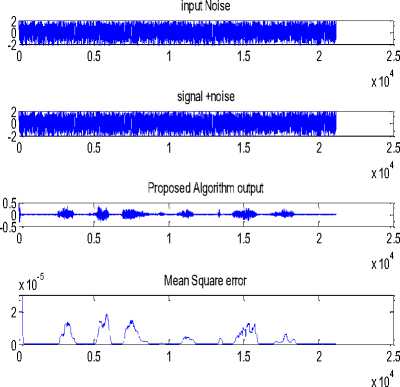
Fig.9. From top to bottom, the original speech, the noise, signal+noise, noise cancelled speech and excessive mean square of proposed algorithm for nonstationary noise ( σ ²max=0.5005)

0    500   1000  1500  2000  2500  3000  3500  4000  4500  5000

signal +noise

-2

0    500   1000  1500  2000  2500  3000  3500  4000  4500  5000

EDNSS Algorithm output

-2

0.5

-0.5 0

500   1000  1500  2000  2500  3000  3500  4000  4500  5000

)^-4                           Mean Square error

x 10 ^-

0    500   1000  1500  2000  2500  3000  3500  4000  4500  5000

Fig.11. From top to bottom, the original speech, the noise, signal+noise, noise cancelled EEG and excessive mean square of EDNSS algorithm for nonstationary noise ( σ ²max=0.5005)

0.5

Input signal

-0.5 :-----------------[------------------[-----------------[------------------[-----------------[------------------:------------------:------------------[-----------------[------------------1

. 0    500   1000  1500  2000  2500  3000  3500  4000  4500  5000

input Noise

-2

0    500   1000  1500  2000  2500  3000  3500  4000  4500  5000

-30

-35

-40

-45

-50

-70

-75

-0        1        2        3        4        5        6        7        8

₂                                    signal +noise

-2

0    500   1000  1500  2000  2500  3000  3500  4000  4500  5000

Proposed Algorithm output

. 0    500   1000  1500  2000  2500  3000  3500  4000  4500  5000

-0.5

Mean Square error x 10-4

0    500   1000  1500  2000  2500  3000  3500  4000  4500  5000

Fig.12. From top to bottom, the original speech, the noise, signal+noise, noise cancelled EEG and excessive mean square of proposed algorithm for nonstationary noise ( σ ²max=0.5005)

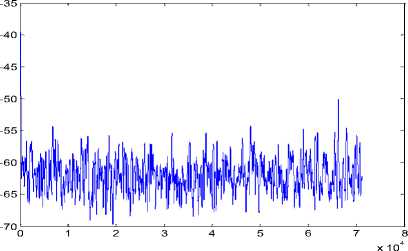
Fig.13. Top to bottom, excessive mean square error of EDNSS and proposed algorithm in dB for nonstationary noise (EEG signal)

Table 1. Comparison of EMSE and Misadjustment for Stationary white noise Mean=0; for speech signal

	σ ²=0.1		σ ²=0.5		σ ²=0.7
Algorithm	M	EMSEss (dB)	M	EMSEss (dB)	M	EMSEss (dB)
EDNESS	0.1424	-56.42	0.5759	-50.36	0.7815	-49.03
Proposed Algorithm	0.1570	-56.00	0.2483	-54.01	0.2911	-53.32

Table 2. Comparison of EMSE and Misadjustment for Stationary noise Mean=0, for EEG signal

	σ ²=0.1		σ ²=0.5		σ ²=0.7
Algorithm	M	EMSEss (dB)	M	EMSEss (dB)	M	EMSEss (dB)
EDNESS	0.1424	-60.27	0.4089	-55.69	0.5315	-54.55
Proposed Algorithm	0.1445	-60.21	0.2021	-58.75	0.2306	-58.18

Table 3. Comparison of EMSE and Misadjustment for Nonstationary noise (Mean=0; σ²min=0.0005) for speech signal

	σ ²max=0.0055		σ ²max=0.0505		σ ²max=0.5005		σ ²max=0.5555
Algorithm	M	EMSEss (dB)	M	EMSEss (dB)	M	EMSEss (dB)	M	EMSEss (dB)
EDNESS	0.0183	-65.33	0.1200	-57.17	0.9586	-48.14	1.0569	-47.72
Proposed Algorithm	0.0982	-58.04	0.1500	-56.20	0.2990	-53.20	0.3156	-52.97

Table 4. Comparison of EMSE and Misadjustment for Nonstationary noise (Mean=0; σ²min=0.0005) for EEG signal

	σ ²max=0.0055		σ ²max=0.0505		σ ²max=0.5005		σ ²max=0.5555
Algorithm	M	EMSEss (dB)	M	EMSEss (dB)	M	EMSEss (dB)	M	EMSEss (dB)
EDNESS	0.0273	-67.45	0.0997	-61.82	0.4226	-55.55	0.4582	-55.20
Proposed Algorithm	0.1171	-61.12	0.1302	-60.66	0.1759	-59.36	0.1813	-59.22

• IV. Conclusion

In this paper modified EDNSS algorithm is proposed and results are demonstrated for both stationary and nonstationary noises at different levels. The simulations and analysis proposed in section III illustrates the advantages of proposed algorithm. The proposed algorithm reduces misadjustment and steady state minimum mean square error, when the signal is corrupted with higher variance level of noise. The algorithm also increases speed of convergence. So the proposed algorithm can be used in speech enhancement applications like automatic noise canceller, echo removal and noise cancellation in digital hearing aids and also can be used in removal of environmental and physiological noise corrupted in EEG signal.

• [1]    Simon Haykin “ Adaptive Filter Theory” Fourth edition pearson education

• [2]    V.Udayashankara “ Modern digital signal processing” second edition PHI

• [3]    Alexander D.Poularikas, Zayed M.Ramadan “Adaptive filtering primer with MATLAB CRC press

• [4]    Zayed Ramadan, &Alexander Poularikas ,Performance Analysis of a New Variable Step-Size LMS Algorithm with Error Nonlinearities IEEE 2004 pp384-388

• [5]    Zayed Ramadan and Alexander Poularikas A Robust Variable Step-Size LMS Algorithm Using Error-Data Normalization IEEE 2005 PP219-224

• [6]    Zayed Ramadan and Alexander Poularikas A Variable Step-Size Adaptive Noise Canceller Using Signal to Noise Ratio as the Controlling Factor IEEE2004 PP 456461

• [7]    Zayed Ramadan and Alexander Poularikas An Adaptive Noise Canceller Using Error Nonlinearities in the LMS Adaptation IEEE 2004 pp3-8

• [8]    Joonwan Kim &Alexander D. Poularikas “Performance analysis of the Adjusted step size NLMS algorithm IEEE 2004 pp 467-571

• [9]    Ma Shengqian, Xu Guowei, Ma Zhifeng, Wei Shuping, Fan Manhong “Research on adaptive noise canceller of an improvement LMS algoritnm 2011 IEEE pp1611-1614

• [10]    K.Sembulingam & Prema Sembulingam “ Essentials of Medical Physiology” 6^th Edition Jaypee 2012

• [11]    P. C. Loizou, “Speech enhancement based on perceptually motivated Bayesian estimators of the magnitude spectrum,” IEEE Trans. Speech Audio Process., vol. 13, no. 5, pp. 857–869, Sep. 2005

• [12]    Boll,S “ Suppression of acoustic noise in speech spectral subtraction” IEEE transactions on acoustics, speech and signal processing. Vol22, Issue2 pages 113-120, 1979,

• [13]    Ephraim Y, Malah D. “Speech Enhancement using a Widrow, Mccool J.M; Laimore,M; Johnsor C.R. “Stationary and nonnstationary learning charactristis of the LMS adaptive filter. IEEE proceedings vol64, Issue 8.

• [14]    Rathnakara.S and Dr.V.Udayashankara “System Identification in Speech Signal Using Modified Kalman Based Normalized Least Mean Square (NLMS) Algorithm”-IJARCSSE Volume 7, Issue 3, March 2017, PP180-184

• [15]    Rathnakara.S and Dr.V.Udayashankara “Real Time System Identification for Speech Signal Implemented on TMS320C6713” IOSR Journal of VLSI and Signal Processing (IOSR-JVSP) Volume 7, Issue 2, Ver. I (Mar. - Apr. 2017), PP 20-25

• [16]    Rathnakara.S and V Udayashankara. Enhancement of Speech    Signal    using    Improved    NLMS

Algorithm. Communications        on        Applied

Electronics 6(9):34-37, April 2017