Estimation of Possible Profit/ Loss of a New Movie Using “Natural Grouping” of Movie Genres

Published Online October 2013 in MECS

A movie [42], also called a film or motion picture, is a series of still or moving images. It is produced by recording photographic images with cameras, or by creating images using animation techniques or visual effects.

Films are cultural artifacts created by specific cultures, which reflect those cultures, and, in turn, affect them. It is considered to be an important art form, a source of popular entertainment and a powerful method for educating or indoctrinating citizens. The visual elements of cinema give motion pictures a universal power of communicat ion.

The process of filmmaking has developed into an art form and has created an industry in itself. Film Industry is an important part of present-day mass media industry or entertainment industry (also informally known as show business or show biz). This industry [61] consists of the technological and commercial institutions of filmmaking: i.e. film production companies, film studios, cinematography, film production, screenwriting, preproduction, post production, film festivals, distribution; and actors, film directors and other film crew personnel.

The major business centers of film making are in the United States, India, Hong Kong and Nigeria. The average cost [43] of a world wide release of a Hollywood film or American film (including preproduction, film and post-production, but excluding distribution costs) is about $65 million. It can be stretched up to $300 million [44] (Pirates of the Caribbean: At World's End). Worldwide gross revenue [45] can be almost $2.8 billion (Avatar). Profit-loss is found to vary from a profit [46] of 2975.63 % (City Island) to a loss [47] of 1299.7 % (Zyzzyx Road). So it will be very useful if we can develop a prediction system which can predict about Film’s business potential.

Many artificial neural network based methods have been used to design for successful Stock Market Prediction [31], Weather Prediction [32] , Image Processing [33], and Time Series Prediction [1], and Temperature Prediction system [2] etc. In this work we have used Backpropagation neural network for prediction of profit/loss of a movie based on some predefined genres. Note that the performance of a backpropagation network mainly depends on choosing an appropriate set of data for training. Intuitively it can be said that the profit of a new movie will be similar to that of an old movie having similar values of genres and other parameters like overall rating giving by the viewers, reputation of the film distributors and present popularity of actor/actress performed for the film. With this idea in mind, we have found a natural grouping of the movies based on their genre values using an MST based clustering method. In this paper we have proposed a training method to train backpropagation neural network for prediction of possible business of a movie [36]. For training, we have chosen a subset of training data from entire training dataset based on the target movie’s features. An MST based clustering method is used to group the movies. The formulation of the problem is presented in the next section. Sec. 2.1

presents the term natural grouping in the context of clustering. Sec. 3 describes our proposed method. Experimental results on 25 movies selected randomly from a given database can be found in Sec. 4. Concluding remarks and scope for further work have been incorporated in section 5.

• II.    STATEMENT OF THE PROBLEM

  Every Film can be identified by certain film genres. In film theory, genre [48] refers to the method based on similarities in the narrative elements from which films are constructed. Most theories of film genre are borrowed from literary genre criticism. Some basic film genres are - action, adventure, animation, biography, comedy, crime, drama, family, fantasy, horror, mystery, romance, science-fiction, thriller, war etc. One film can belong to more than one genre. As an example the movie titled “Alice in Wonderland (2010)” belongs to [49] action, adventure, and fantasy genres.

• 2.1    The importance of natural grouping in generation of training data sets

Any film’s success is highly dependent on its film genres. Other important factors are reputation of Film Studio or Production house and present popularity of casted actor/actress. We have considered these genres and the said factors as a Film’s attributes. We can then collect the values for those attributes for several films released in the past. Based on these data we can estimate/ predict the possible future business of an upcoming Film.

We have used 20 movie genres like action, adventure, animation, biography, comedy, crime, documentary, drama, family, fantasy, history, horror, musical, mystery, romance, science fiction, sport, thriller, war, and western. Note that the factors such as the overall rating giving by the viewers, reputation of the film distributors and present popularity of actor/actress performed for the film, has been taken care of by the inclusion of the following 3 attributes- film distributor’s reputation, overall rating and casting rating.

Our movie database consists of 395 Hollywood movies released in the year 2009, 2010 and 2011. We have chosen a subset of 25 movies from our movie database for testing purpose. Remaining 370 movies used for training of the backpropagation neural network. The movies that belong to this subset are then divided into a number of “natural groups” based on the similarity of the film’s attributes as stated above. The notion of natural grouping is explained in the next subsection. Note that, one can expect desirable result if the neural network can be trained with those movies which have similar genre values as that of the target movie.

Note that Clustering can be used as a technique to find similarity or dissimilarity among the objects. Our objective here is to partition the training database into a number of “natural groups”, such that, movies belonging to a particular group are similar to each other with respect to their attribute values and movies belonging to different groups are dissimilar on the same basis. Here our intention is to train the neural network with a data of a particular group of movies which are similar to that of the target movie.

Clustering in true sense is an unsupervised technique used in discovering inherent structure present in the set of objects. Clustering is a technique used to group data points of similar type from a heterogeneous collection of data points.

Let the set of patterns be S = ^{d 1 , d₂, d₃,..., d m } E Rⁿ where d_i is the i_th pattern vector corresponding to i_th movie, m is the total number of movies in a given set of movies and n is the dimensionality of the feature space. Since we have considered 23 movie attributes hence the value of n for our experiment is twenty three.

• P2. C j AQ * Ф , f°ri * j ^and

• P3. U^K₌₁ C_t = S, where Ф represents null set.

Clustering techniques may broadly be divided into two categories: hierarchical and non-hierarchical. The non-hierarchical or partitional clustering problem deals with obtaining an optimal partition of S into K subsets such that some clustering criterion is satisfied. Among the non-hierarchical clustering techniques, the K-means (or C-means or basic Isodata) algorithm has been one of the more widely used algorithms. This algorithm is based on the optimization of a specified objective function. It attempts to minimize the sum of squared Euclidean distances between patterns and their cluster centers. It was shown in [19] that this algorithm may converge to a local minimum solution. Moreover it may not always detect the natural grouping in a given data set, though it is useful in many applications.

A lot of scientific effort has already been dedicated to cluster analysis problems, which attempts to extract the “natural grouping”, present in a data set. The intuition behind the phrase “natural group” is explained below in the context of data set in R2.

For a data set M = ^{d 1 , d₂, d₃, ., d m } E R² obtain the scatter diagram of M. By viewing the scatter diagram, what one perceives to be the groups present in M is termed as natural groups of M . For example, for the scatter diagram shown in Fig. 1.1(a), the groups that we perceive are shown in Fig. 1.1(b). Similarly for the scatter diagrams shown in Fig. 1.2 (a), the natural groups are as shown in Fig. 1.2(b).

Figure 1.1(a) Scatter diagram of synthetic data with noise

Figure 1.1(b) Clustering by the proposed method

Figure 1.2(a) Scatter diagram of synthetic data with noise

Figure 1.2 (b) Clustering by the proposed method

Clustering techniques [18, 27-30] aim to extract such “natural groups” present in a given data set and each such group is termed as a cluster. So we shall use the term “cluster” or “group” interchangeably in this paper. Existing clustering techniques may not always find the natural grouping. The method for obtaining the natural groups in R2can also be extended to Rp (p > 2) . Note that, the perception of natural groups in the data set is not possible for higher dimensional data. But the concept used for detecting the groups in R2 and R3 may also be applicable to higher dimensional data to obtain a mean ingful grouping.

In this paper we have proposed an algorithm that uses MST of data points for finding the “natural grouping” of the given set of movies to be used for training. The important characteristic of the proposed method is that, given a data set, it can obtain the partitions automatically without knowing the value of K. It may be noted that a function which takes into account all the interpoint distances of S is the sum of edge weights of minimal spanning tree of S, where the edge weight is taken to be the Euclidean distance. If we represent the sum of the edge weight of minimal spanning tree [21] of S by l_m then it can be noted that l_m ⟶ ∞ in probability as m ⟶ ∞ and ^lm ⟶ 0 in probability as m ⟶ ∞.

Thus the threshold T for the cluster separation is taken to be equal to T = lm , where lm is the sum of the edge weights (edge weight is taken to be the Euclidian distance) of minimal spanning tree of S. Note that T is a function of interpoint distances in S as well as the number of points m.

Note that a similar such function is used in [38]. Our proposed method accepts movies as input and assigns then into different groups based on their attributes. MST of data points are used to compute the above mentioned threshold for cluster separation. The definition of MST and how it is used to obtain the natural grouping are described below.

Given a connected, undirected graph G = < V, E >, where V and E are set of vertices and edges respectively, the minimum spanning tree problem is to find a tree A = < V, E^′ > such that E^′ subset of E and the cost of A is minimal. Note that a minimum spanning tree is not necessarily unique. It is important to remember that a tree over |V| vertices contains |V|-1 edges. A tree can be represented by an array of this many edges.

In this method, at first the movies are considered as individual vertices. The weight of the edges connecting the vertices is nothing but the Euclidean distance between their respective pattern vectors.

Initially we consider an empty set A and at every stage the smallest edge not present in A should be selected. Since a tree does not have a cycle, a cycle cannot be formed while selecting the edges. The entire method is continued unless all the vertices (movies) are included in the MST. In this way a minimal spanning tree is formed from the given input movies as data points.

The next task is to find out the sum of the edge weights present in the spanning tree A. Then the sum is divided by the no. of movies (given as input) to obtain the threshold T (as mentioned in the earlier section.).Then all edges whose weights are greater than F *T, where F is a constant (In our experiment we choose F = 1.175, since this value provided consistently good results) are removed from the spanning tree A, yielding few disjoint graphs. The vertices of the individual trees are categorized into same cluster. There may be trees with a single node that indicates that the node is a lone member in that particular cluster.

We have taken the Euclidean distances from our target movie to all the cluster centers (cluster’s center can be obtained from the cluster obtained in the previous process). We have used to train our neural network with the movies belong to same cluster with minimum distance from our target movie. This trained neural network is used to predict business of the target movie.

Artificial neural network [24] learning methods provide a robust approach to approximating real-valued, discrete-valued, and vector-valued target functions. For certain types of problems, such as learning to interpret complex real-world sensor data, artificial neural networks are among the most effective learning methods currently known. Artificial neural networks have been applied in image recognition and classification [3], image processing [25], feature extraction from satellite images [4], cash forecasting for a bank branch [5], stock market prediction [22], decision making [6], temperature forecasting [7], atomic mass prediction [41], Prediction

Movie Genres of Thrombo-embolic Stroke [8], time series prediction [9], forecasting groundwater level [10].

Backpropagation is a common method of teaching artificial neural networks about how to perform a given task. It is a supervised learning method. It is most useful for feed-forward networks [51].

Backpropagation neural network is successfully applied in image compression [11], satellite image classification [12], irregular shapes classification [13], email classification [14], time series prediction [34], bankruptcy prediction [15], and weather forecasting [35].

• III.    THE PROPOSED METHOD

As stated above we have used an MST based clustering method to find the “natural grouping” of a given set of movies that are used for training of the backpropagation network for prediction of possible profit / loss of a new movie. This method of grouping requires no apriory knowledge about the number of such natural groups. The intuition behind the phrase “natural groups” is explained in the context of data set in R2 in the Sec. 2.1.

It seems that if the backpropagation neural network is trained with those movies that are having similar attribute values to the target movie we may get better results than that of the normal training process. Possibly this type of training method will reduce the neural network’s complexity, training time, computation time.

In this paper we have used the proposed training methods and also the normal training methods to train multilayer feed-forward neural network. We have compared the result obtained for the said two methods in Table 1. In the normal training method (Experiment 1) we have used all the movies from training data set to train the neural network which is used to predict the profit percentage of a target movie. In our proposed training algorithms (Experiment 2) we have used MST of data points for finding the “natural grouping” of the given training set of movies. This MST of data points are used to compute the threshold for cluster separation. We have taken the Euclidean distances from our target movie to all the cluster centers (cluster’s center can be obtained from the cluster obtained in the previous process). We have used to train our neural network with the movies belong to same cluster with minimum distance from our target movie. Note that, a multilayer feed-forward neural network consists of an input layer, one or more hidden layers, and an output layer.

Here the backpropagation algorithm [23] performs learning on the said multilayer feed-forward neural network. It iteratively learns a set of weights for prediction of the profit/ loss percentage (10 scales) label of instances. A typical multilayer feed-forward network is shown in Fig. 2.

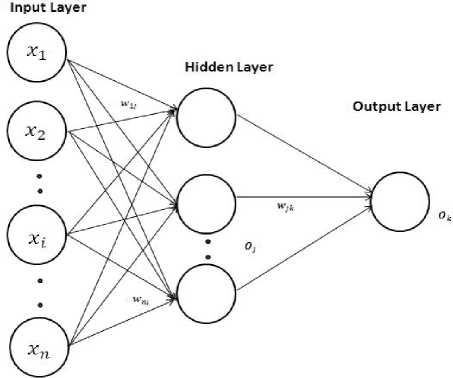
Figure. 2. A multilayer feed-forward neural network.

Since we have 23 attributes (20 film genres, film distributor’s reputation, overall rating and casting rating) to consider for this method, we need 23 nodes in the input layer. We have taken 10 nodes in the hidden layer and one node in the output layer. Note that there is no strict guide line to choose the number of nodes in a hidden layer. However, usually the number of nodes in the hidden layer is to be between the input layer size and the output layer size. We have experimented using different number of nodes in the hidden layer but we have obtained consistently good result in respect of learning speed with ten nodes in the hidden layer.

Note that input nodes have received real numbers that represents the values of the individual genres. A positive (negative) real number is generated at the output node which indicates the predicted profit (loss) of the movie of under consideration.

We have used 395 movie’s data released from 2009 to 2011.For training of the said network we have used movies belong to the natural group which is nearest to our target movie. After the network has been successfully trained it can be used for prediction of profit/loss of new movie to be released. In our experiment we have taken some of the released movie (not taken in the training set) of 2010 for evaluating the efficiency of the trained backpropagation network. The experimental results are presented at the Sec. 4.

• 3.1    Algorithm 1(To find natural grouping of the movies for training)

The notations used in this algorithm are: G: graph containing all the vertices (all movies) and the edges (edge weights are the inter-vector distances), Wij : edge weights from vertex i to vertex j, T: threshold for the cluster separation (to be computed as stated above), Si, Sj : pattern vectors corresponding to the ith and jth movies respectively, Φ: null set.

Step 1: Л ^ Ф // A is a sub-graph of G

Step 2: Wy is calculated for all movies where W j is the Euclidian distance from S ^ to S j

Step 3: The edges of G are sorted in increasing order of W y

Step 4: For any edge E (considered in sorted order); if the endpoints of E are disconnected in A , E is added to A . Step 5: Repeat step 4 till all the vertices (of G ) are included in A .

Step 6: If Wy >1.175 *T then Wy = —1 for all i, у Step 7: For edges with W j * — 1 , the vertices i, j connected by the edges are placed in the same cluster.

Step 8: For vertices where all the connecting edges have W j = — 1are placed in separate clusters where the said vertex (movie) is the sole member.

Step 9: Stop

Note that initially all the movies are considered to be in the same cluster. Then by using the threshold T, the MST is splitted into small sub-graphs. Each of which corresponds to a separate cluster. The clusters may contain one or more than one members. These clusters are the natural groups obtained by the above mentioned MST based methods.

As stated above, there is 23 film attributes to form the pattern vector for each movie. Thus each movie is represented as a point in multidimensional feature space. Natural groupings of these data points then obtained by the proposed MST based methods as stated above.

• 3.2    Algorithm 2 (To select the appropriate group of movies for training)

• 3.3    Algorithm 3 (For learning of the backpropagation neural network)

The following algorithm selects the appropriate group of movies which will be used for neural network training of the backpropagation neural network.

Step 1: For a given target movie compute the Euclidian distance from its pattern vector to all the cluster centers obtained by the method stated in algorithm 1.

Step 2: Find the cluster center for which the distance is minimum.

Step 3: Select the movies belonging to the cluster found in step 2 for training purpose.

Step 4: Stop

Algorithm 2, in fact, selects a subset of the movies given for training of the neural network. Here we have used backpropagation neural network for prediction of possible profit/loss of the movies. The backpropagation learning algorithm used in this work is stated below.

Input:

• •    D , a data set consisting of the movies that

belongs to the cluster(C) which is nearest to our target movie.

• •    l , the learning rate;

Output:

A trained neural network, which can predict profit percentage.

Method:

Step 1: Initialize all weights and biases in network ;

Step 2: While terminating condition is not satisfied {

Step 3: For each training instance X in D {// propagate the inputs forward:

Step 4: For each input layer unit j

Step 5: Oy = j // output of an input unit is its actual input value

Step 6: For each hidden or output layer unit j {

Step 7: f = 2 , W_t j O , + 0 j ;//compute the net input of unit j with respect to the Previous layer, i

Step 8: Oj = — -—г ;} // compute the output of each unit j// Back propagate the errors:

Step 9: For each unit j in the output layer

Step 10: Err =Oj(1 — Oj )(T — Oy); // compute the error

Step 11: For each unit j in the hidden layers, from the last to the first hidden layer

Step 12: Err = Oj (1 - Oy) Ek Errk wjk ;// compute the error with respect to the next higher Layer, k

Step 13: For each weight Wy in network {

Step 14: Aw^ = (l)En j O , ; // weight increment

Step 16: For each bias 0 j in network {

Step 17: A0 j =(l )Err j ; // bias increment

Step 18: 0 j =0 j + Л 0 j ; }// bias update

Step 19: }}

Step 20: Stop

At first, the weights in the network are initialized to small random numbers [23], bias associated with each unit also initialized to small random numbers.

The training instance from movie database is fed to the input layer. Next, the net input and output of each unit in the hidden and output layers are computed. A hidden layer or output layer unit is shown in Fig.3.

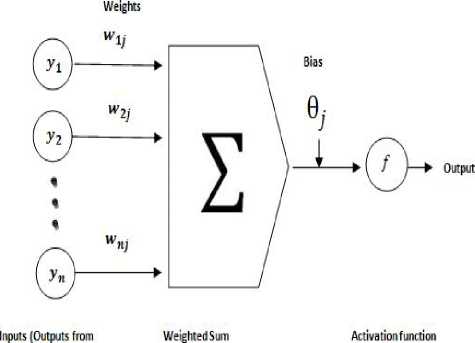
previous layer)

Figure 3. A hidden or output layer unit j

The net input to unit j is l = Si wtJ ° + 9

Where, w ij is the connection weight from unit i, in the previous layer to unit j; G i is the output of unit i from the previous layer; and 9 j is the bias ofthe unit.

As shown in the Fig. 2, each unit in the hidden and output layers takes its net input and then applies an activation function to it. The function (sigmoid) symbolizes the activation of the neuron represent by the unit. Given the net input I j to unit j, thenG j , the output of unit j computed as

^O j =

1+e-iJ

The error of each unit is computed and propagated backward. For a unit j in the output layer the error Erf j is computed by

Err = O j (1 -O j )(T j - O j ) (3) where, G j is the actual output of unit j, and T j is the known target value of the given training instance. The error of a hidden layer unit j is

^Erj j = 0 j (1 ^- O j ⁾ X_k^Ejj_k W j _k (4) where, W jk is the weight of the connection from unit j to a unit k in the next higher layer, and Err_k is the error of unit k .

The weights and biases are updated to reflect the propagated errors. Weights are updated by the following equations, where Aw ij is the change in weight w ij

Aw_t j = (Z ^)Err_s O i (5)

w_tj = w_t j + Aw_t j (6)

l is the learning rate. In our experiment it is 0.1.

Biases are also updated, if A9 j is the change in 9 j then

И 9_j =(l)Erj j 9_j=9_j + Д 9_j

The weight and bias increments could be accumulated in variables, so that the weights and biases are updated after all of the instances in the training set have been presented. In our experiment we have used this strategy named epoch updating, where one iteration through the training set is an epoch.

The training stops when

• •    All Д w_t j in the previous epoch were so small as

to be below some specified threshold, or

• •    The percentage of instance misclassified in the previous epoch is below some threshold, Or

• •    A pre specified number of epochs have expired.

In our experiment we have specified the number of epochs as 1000.

After successful training of the backpropagation neural network it is used for prediction of possible profit/ loss of a given movie selected form test data set of movies. The experimental results obtained are presented in the next section.

• IV.    EXPERIMENTAL RESULT

  We have carried out our experiments on a movie database containing 395 American films with 23 attributes (20 film genres, film distributor’s reputation, overall rating and casting rating), released from 2009 to 2011. The data about investment and earnings of all the movies are obtained from Wikipedia ( http://en.wikipedia.org ) and rating and genres of the movies are obtained from imdb ( http://www.imdb.com/ ).

We have used 370 movies out of the total 395 movies to train the neural network. The attributes of the remaining 25 movies are used as input of the trained network to predict the possible profit/ loss.

In our first experiment (Experiment 1), we have used all the 370 movies of the training data set to train the neural network. The attributes of the target movie from test set are used as input of the trained network to predict the possible profit/ loss.

Unlike Experiment 1, in our second experiment (Experiment 2), we have used an appropriate subset of the complete training set of movies to train the neural network for prediction of possible profit/ loss of each given movie selected from the test set. In fact for each movie for which the prediction of possible profit/ loss is sought, we compute an appropriate subset of movies from the training set by using our proposed MST based method to train the backpropagation neural network for prediction. Then the attributes of the target movie are used as input of the trained network to predict the possible profit/ loss. We have carried out our experiment with 25 movies from our test set.

The experimental results obtained from Experiment 1 and Experiment 2 are presented in Table1. In table 1, the first column presents name of the 25 movies from the test set selected for experimentation both with Experiment 1 and experiment 2. The second column shows the actual profits made by those movies. Percentages of possible profit/ loss predicted by the method used in experiment 1 are listed in Column 3. Percentage of error committed by experiment 1, for each movie has been narrated in column 4. Similarly column 5 and 6 represent prediction of possible profit/ loss and percentage of error respectively, obtained by our proposed method used in Experiment 2.

It can be shown from Table 1 that the possible profit/ loss prediction by Experiment 2 yield percentage error rate of less that 5% for 15 numbers of movies, 5-10% for 4 number of movies and greater than 10% for 6 numbers of movies. Note that for Experiment 1, predicted possible profit/ loss provided percentage error rate of less that 5% for 6 numbers of movies, 5-10% for 5 number of movies and greater than 10% for 14 numbers of movies

TABLE 1 . Experimental results (up to two decimal places)

Movie Name (A)	Actual Profit in percentage (B)	Profit percentage ( Experiment 1) (C)	Percentage of error (Experiment 1) (D)	Profit percentage ( Experiment 2) (E)	Percentage of error ( Experiment 2) (F)
Blue Valentine	1135.57	521.10	54.11	1178.65	3.79
Case 39	4.41	19.00	330.92	3.66	16.99
Conviction	-22.32	-98.23	340.10	-17.80	20.23
Cyrus	41.77	48.41	15.90	44.31	6.08
Clash of the Titans	294.57	263.59	10.52	308.06	4.58
Daybreakers	157.08	190.17	21.06	169.28	7.76
Dinner for Schmucks	25.23	81.74	224.01	25.08	0.60
Due Date	225.72	290.06	28.51	230.20	1.99
Eat Pray Love	240.99	212.72	11.73	215.43	10.61
Faster	48.10	49.73	3.39	46.72	2.86
Grown Ups	239.29	242.89	1.51	236.55	1.15
Hereafter	163.00	164.80	1.11	170.98	4.90
Inception	415.99	338.02	18.74	356.52	14.29
Leap Year	71.62	65.63	8.37	80.63	12.58
Life as We Know It	178.02	156.02	12.36	182.08	2.28
Megamind	147.30	158.99	7.93	139.41	5.361
My Soul to Take	-16.10	21.85	35.78	-10.51	34.68
Salt	168.83	178.65	5.82	172.52	2.19
Tangled	127.20	122.32	3.84	125.46	1.37
The Bounty Hunter	240.81	269.06	11.73	235.17	2.34
The Expendables	243.09	238.58	1.85	240.98	0.87
The Kids Are All Right	767.65	805.31	4.91	751.27	2.13
The Next Three Days	109.16	117.83	7.94	110.06	0.82
The Twilight Saga: Eclipse	927.19	835.12	9.93	905.91	2.30
Wall Street: Money Never Sleeps	92.50	80.10	13.41	84.07	9.11

It may also be noted that experiment 2 has provided a percentage error of less than 1% for two movies. Fig. 4 represents the results of experiment 1 and experiment 2 in the form of bar chart. Thus it may be concluded that our proposed method using appropriate subset of training data has provided much better result than that of the conventional method of using the complete training set.

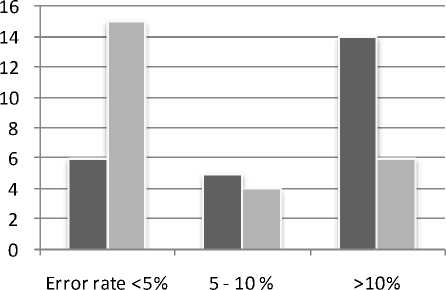
■ Experiment 1 (Number of Movies)

■ Experiment 2 (Number of Movies)

Figure 4 . Comparison between two experiment results

• V.    CONCLUSION AND SCOPE FOR FURTHER WORK

It is obvious from the experimental result presented above that our proposed training method using a subset of movies (that are similar to the target movie in terms of film attributes) selected from the given training set has provided much better result in predicting the possible profit/ loss of a given target movie. Thus it may be concluded that it is better to use an appropriate subset of the training set rather than using complete training set (done for experiment 1) for better prediction of possible profit/ loss. It may be noted that the proposed method used in experiment 2 has provided an error rate of even less than 5% for 60 percent of the target movies selected for experimentation.

Note that, it is very difficult even for a human expert to predict the possible profit or loss of a new movie to be released. It seems that the genres of the movie play a significant role in the profit of the movie but it is very difficult to analytically establish the relation of the value of the genres of a given movie with the profit that it makes. In this paper we have attempted to develop a heuristic method using backpropagation neural network with an appropriate subset of the complete training set for training of the neural network to solve this problem.

Further research work can be conducted in the following areas. We can search for more genres and/or division of an existing genre into subgenres that may led to a higher success rate of prediction. Also we can conduct research for finding features of profitable movie trend in terms of some specific genres possibly using a psychological analysis of peoples’ likings or interests in some specific kinds of movies.