Evaluating Overheads of Integrated Multilevel Checkpointing Algorithms in Cloud Computing Environment

Published Online June 2012 in MECS

Cloud computing [1], [2], [3] is currently emerging as a powerful way to transform the IT industry to build and deploy custom applications. In cloud environment jobs keep on arriving to the data centers for execution and nodes will be allocated to the jobs for their execution as per their requirements and successfully executed jobs will leave the nodes. In this scenario it may possible that some nodes will become inactive while executing threads due to some failure. So there is need of efficient failover strategy for handling failures as it may cause restartation of entire work, whether some threads of the job has been successfully done on other nodes. In case of node failure, that means, the node is no longer accessible to service any demand of clients, the cloud must migrate jobs to the other node.

A checkpoint is a local state of a job saved on stable storage. By periodically executing the checkpointing, one can save the status of a process at consistent intervals

[17], [18]. If there is a failure, one may resume computation from the earlier checkpoints, thereby, avoiding restating execution from the beginning. The process of restarting computation by rolling back to a consistent state is called rollback recovery. In cloud computing environment, since the nodes in the data centers do not share memory [19], therefore it is required to transfer the load of failed node to other nodes in case of any sort of failure.

In this paper, checkpoints are integrated with load balancing algorithms for data centers (cloud computing infrastructure) has been considered, taking into account the several constraints such as handling infrastructure sharing, availability, failover and prominence on customer service. These issues are addressed by proposing a smart failover strategy which will provide high availability to the requests of the clients. New cloud simulation environment has been purposed in this paper, which has the ability to keep all the nodes busy for achieving load balancing and also execute checkpoints for achieving failover successfully.

An integrated checkpointing algorithm implements in parallel with the essential computation. Therefore, the overheads presented due to checkpointing should need to be reduced. Checkpointing should enable a CSP to provide high availability to the requests of the clients in case of failure, which demands frequent checkpointing and therefore significant overheads will be introduced. So it becomes more critical to set checkpointing rerun time. Multilevel checkpoints [9], [10], [11], [12], [13], [14], [15] are used in this research work for decreasing the overheads of checkpoints.

• A. Parameters and Metrics used in this paper

TABLE I. Parameters and Metrics used in this paper

Parameter name	Meaning
C	Checkpoint overhead
L	Checkpoint Latency
R	Time required for job migration
t	Time spent on computation
t1	No. of time C runs
t2	No. ot time R occurs
r	Chcekpointing ratio

G(t)	Expected time for computation
Thp	Throughput
WTR	Waiting threads
NTR

Table I is showing the different parameters and metrics that are used in this research work along with their meaning. Maximum Execution Time(MaxET), Minimum Execution time(MinET), Maximum Waiting Time(MaxWT) and Minimum Waiting Time(MinWT) are different metrics used in this research paper for performance comparisons. However some other parameters are also considered for comparing developed simulator and existing methods.

• II.    PROBLEM DEFINITION

Checkpointing is a technique to reduce the loss of computation in the manifestation of failures. Two metrics can be used to illustrate a checkpointing scheme:

• (i)    Checkpoint overhead (increase in the execution time of the job because of a checkpoint implementation).

• (ii)    Checkpoint latency (duration of time required to save the checkpoint).

This research work evaluates the expression for “checkpointing ratio (R)”' of the checkpointing scheme as a function of checkpoint latency and overhead. Main objective of this paper is to determines the optimal checkpoint interval ``checkpointing rerun time''. However to decrease checkpointing overheads multilevel checkpointing [9], [10], [11], [12], [13], [14], [15] is also used.

• III.    RELATED WORK

Availability [6] is a reoccurring and a growing concern in software intensive systems. Cloud systems services can be turned offline due to conservation, power outages or possible denial of service invasions. Fundamentally, its role is to determine the time that the system is up and running correctly; the length of time between failures and the length of time needed to resume operation after a failure. Availability needs to be analysed through the use of presence information, forecasting usage patterns and dynamic resource scaling.

Checkpoint [1], [2] is defined as a designated place in a program at which normal processing is interrupted specifically to preserve the status information necessary to allow resumption of processing at a later time. By periodically invoking the check pointing process, one can save the status of a program at regular intervals. If there is a failure one may restart computation from the last checkpoint thereby avoiding repeating the computation from the beginning.

There exist many models to describe checkpoint systems implementation. Some of the models use multilevel checkpointing approach [9], [10], [11]. Many researchers have worked to lower the overheads of writing checkpoints. Cooperative checkpoints reduce overheads by only writing checkpoints that are predicted to be useful, e.g., when a failure in the near future is likely [12]. Incremental checkpoints reduce the number of full checkpoints taken by periodically saving changes in the application data [13], [14], [15]. These approaches are orthogonal to multilevel checkpoints and can be used in combination with our work. The checkpoint and rollback technique [4] has been widely used in distributed systems. High availability can be offered by using it and suitable failover algorithms.

The ZEUS [5] Company develops software that can let the cloud provider easily and cost-effectively offer every customer a dedicated application delivery solution. The ZXTM [4],[5] software is much more than a shared load balancing service and it offers a low-cost starting point in hardware development, with a smooth and cost-effective upgrade path to scale as your service grows.

The Apache Hadoop [7] software library is a framework that allows for the distributed processing of large data sets across clusters of computers using a simple programming model. It is designed to scale up from single servers to thousands of machines, each offering local computation and storage. Rather than rely on hardware to deliver high availability, the library itself is designed to detect and handle failures at the application layer, so delivering a highly available service(s) on top of a cluster of computers, each of which may be prone to failures.

JPPF [8] is a general-purpose Grid toolkit. Federate computing resources working together and handle large computational applications. JPPF uses divide and conquer algorithms to achieve its work successfully. ZXTM [4], [5], Apache Hadoop [7] and JPPF [8] not provide feature of checkpoints.

Checkpointing overheads [20], [21], [22], [23] have been discussed by many researchers. An integrated checkpointing algorithm implements in parallel with the essential computation. Therefore, the overheads presented due to checkpointing should need to be reduced. Much of the previous work [20], [21], [22], [23], [24], [25], [26] present measurements of checkpoint latency and overhead for a few applications.

Several models that define the optimal checkpoint interval have been proposed by different researchers. Young proposed a first-order model that describes the optimal checkpointing interval in terms of checkpoint overhead and mean time to interruption (MTTI). Young’s model does not consider failures during checkpointing and recovery [29], while Daly’s extension lead of Young’s model, a higher-order approximation, does [30]. In addition to considering checkpointing overheads and MTTI, the model discussed in [28] includes sustainable I/O bandwidth as a parameter and uses Markov processes to model the optimal checkpoint interval. The model described in [31] uses useful work, i.e., computation that contributes to job completion, to measure system performance.

• IV.    CHECKPOINT LATENCY AND OVERHEAD

The checkpoint latency [27], [28] era is separated into two types of execution: (1) useful computation, and (2) execution necessary for checkpointing. The two types are usually enclosed in time. However, for modelling purposes, it can be assumed that the two types of executions are divided in time, as shown in Fig. 1. As shown in the Fig. 1, the first C units of time during the checkpointng latency era is supposed to be used for saving the checkpointing. The lingering (L - C) units of time is supposed to be consumed for useful execution of jobs. Even though the C units of overhead are modelled as being acquired at the commencement of the checkpoint latency era, the checkpoint is considered to have been recognised only at the end of the checkpoint latency era.

• B ．    Failure occur during checkpoint latency

A failure occurs sometime during the interval. When a failure occurs, the task must be rolled back to the previous checkpoint, incurring an overhead of R time units. In Fig. 3, the task is rolled back to checkpoint1 (CP1). After the rollback, L - C units of useful computation performed during the latency period of checkpoint CP1 must be performed again, this is necessary, because the state saved during checkpoint CP1 is the state at the beginning of the latency period for checkpoint CP1. In the absence of a further failure, additional T + C units of execution are required before the completion of the interval. Thus, after a failure, R + (L - C) + (T + C) = R + T + L units of execution is required before the completion of the interval, provided additional failures do not occur.

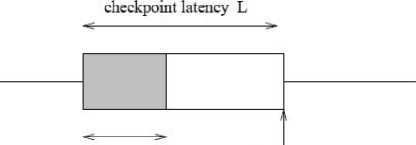
checkpoint            the checkpoint is considered overhead C           "established1' only at the end of die checkpoint latency period

Fig. 1 Modelling checkpoint latency and overhead (adapted from [27])

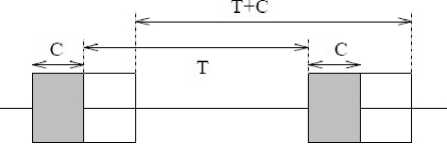
L

L-C

Even though the above representation of checkpoint latency and overhead is abridged, now it is required to exhibit that it will lead to perfect exploration. Two discrete conditions may arise when an interval is executed.

A ． No failure occur during checkpoint latency

L-C units of useful computations is performed during the latency period

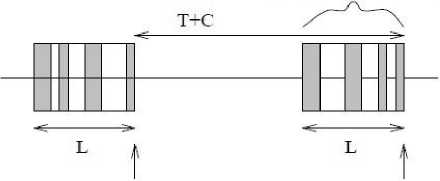
interval begins interval ends

Fig. 2 If no failure will occur during checkpoint latency (adapted from [27])

interval begins

interval ends

Fig. 3If failure occur during checkpoint latency (adapted from [27])

Now consider Fig. 3, when the failure occurs, as shown in Fig. 3, the system can be considered to have rolled back to the end of the ``shaded portion’’ in the latency period for checkpoint CP1. (Note that no state change occurs during the ``shaded portion".) Now it is apparent that, in the absence of further failure, R + T + L units of execution are required to complete the interval. Thus, this representation of checkpoint latency and overhead yields the same conclusion as the more accurate representation in Fig. 2.

• V.    CHECKPOINTING OVERHEAD RATIO

The main goal of this research is on understanding the effect of checkpoint latency on performance. The objective is not on offering elaborate prototypes for checkpointing structures, as in many previous works. Consequently, this paper uses a simple prototype that is adequate for purposed work. For instance, it is assumed that C and L are constants for a given scheme. A more elaborate model may undertake C and L to be some function of time.

Let G(t)[27], [28] denote the expected (average) amount of execution time required to perform t units of useful computation. (Useful computation excludes the time spent on checkpointing and migration of jobs.) Then, overhead ratio (r) can be defined as:

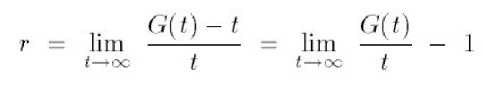
Fig. 4 Checkpoint overhead ratio (adapted from [27])

Note that r will always remain greater than 0 as it is well known some overheads always present in the computation. Smaller the r states that low overheads are there. As the objective of this research to find optimal interval time overhead ratio is rewrite using the following expression:- r= ( TET + t1(C) + t2(R) )/t (adapted from [27])

• VI.    PURPOSED FAILOVER STRATEGIES

In order to achieve high availability for cloud computing using checkpoints based load balancing algorithms, two algorithms has purposed in this research work. Checkpoints based load balancing is defined as the feasible allocation or distribution of the work to highly suitable nodes so that execution time of the job could be minimized. This section discusses the procedure that how checkpoints based load balancing algorithms works and later on how proposed integrated checkpointing algorithms will provide high availability to the requests of the clients. Fig. 5 is showing the three tier architecture for cloud environment. Fig. 5 has shown that there is a request manager (central cloud), clients send their requests to it all other nodes and their connectivity not deal directly with the clients. Thus request manager allow clients to submit their jobs. Then request manager first divide the given job into threads and also allocate one of

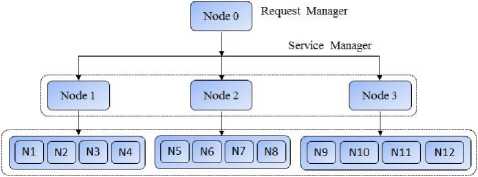
Service Nodes

Fig. 5 3-Tier Architecture

A ． Proposed load balancing algorithms

Proposed load balancing algorithms are developed considering main characteristics like reliability, high availability, performance, throughput, and resource utilization. However to fulfill these requirements of failover strategies, in Fig. 6 and Fig. 7 two different flowcharts named as global flowchart and local flowchart are shown. To decrease checkpointing overheads by using multilevel checkpointing [6], [7], [8], [9], [10], [11], [12], two different algorithms are used in this research work.

The flowchart of global checkpointing algorithm is shown in Fig. 6 that shows how global algorithm will work? It will take the following steps to assign the subcloud to the requests of the clients:

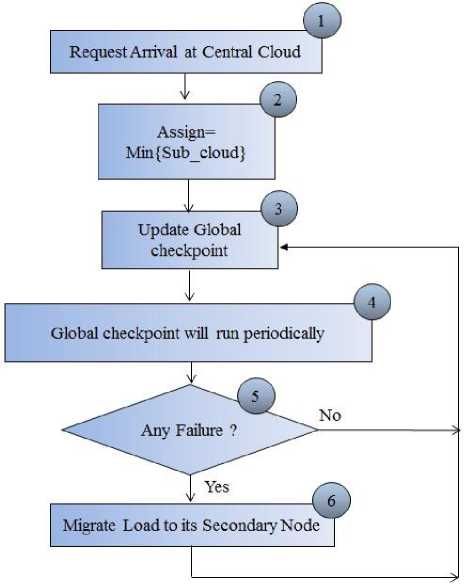
Fig. 6. Global Checkpointing Algorithm’s Flowchart

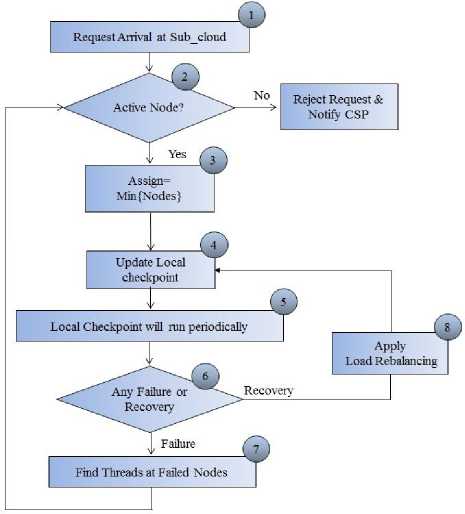
Fig. 7. Local Checkpointing Algorithm’s Flowchart

Step 2: CSP divide the jobs into threads and then allocate a minimum loaded subcloud to the jobs.

Step 3: After allocation of the sub cloud, global checkpoint will be updated.

Step 4: Global checkpoint will run periodically.

Step 5: By reading checkpoint CSP will check whether any subcloud has failed or no failure occur. If no failure will occur then a new save-point will be created and global checkpoint will be updated.

Step 6: If failure is found then work will be migrated from failed node to failed node’s secondary node and global checkpoint will be updated.

Fig. 7 is showing the flowchart of local checkpointing algorithm, which will work on sub cloud. This algorithm will applied on sub clouds and also nodes attached to it. It will take the following steps to allocate the nodes to the threads:

Step 1: Firstly threads will arrive on the subcloud.

Step 2: Then subcloud will check that whether any node is active or not? If no node is active then CSP will be notified by a message that “Subcloud is not responding”.

Step 3: Then subcloud allocates minimum loaded nodes to the threads in such a way that load remains balance on the nodes.

Step 4: Local checkpoint will be updated.

Step 5: Global checkpoint will run periodically and a new save-point will be created every time.

Step 6: By reading checkpoint CSP will check whether any node has found to be failed or any node has recovered from failure.

Step 7: If any node found to be failed then subcloud will shift that node’s load to the currently active nodes in such a way that load remain balance on active nodes and local checkpoint will be updated.

Step 8: If any node has been recovered then it will take load of some of other nodes which are heavy loaded and local checkpoint will be updated.

• VII.    EXPERIMENTAL SETUP

In order to implement the purposed failover strategy a suitable experimental set-up has been made as shown in Fig. 8. It takes following steps to execute the jobs of the clients:

Step 1: Firstly clients submit their requests to the CSP via internet.

Step 2: CSP then allocate one of the subclouds to the Step 3: After Step 2 local algorithm come in action. Each subcloud paramount chooses threads in FIFO fashion and allocate lightly loaded node to it.

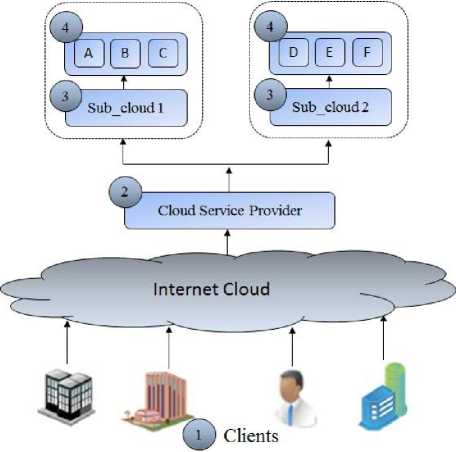
Fig. 8. Simulator Environment

• VIII.    SIMULATION RESULTS

Table II give the inputs that are given to the simulator. In Table II various Jobs are given with their serial execution time and also if jobs will execute in parallel then how many numbers of threads can be made from it or how many nodes are required to run given job in parallel fashion.

TABLE II. INPUTS TO THE SIMULATOR

Job Name	Threads	Serial Time
1	2	4
2	3	8
3	3	14
4	2	17
5	1	8
…..	……	……
100	2	25

• A.    Global Checkpoint

Designed simulator first divides job into threads and allocate sub clouds to them in FIFO fashion and global checkpoint will be updated. Global checkpoint gives the detail such as which job is going to be run on which sub cloud and also other relevant information like entered time of job, number of processors required, serial time, thread time etc.

• B.    Local checkpoint

Fig. 9 is showing the local checkpoint in it nodes has been allocated to threads. For all nodes whether it belong to sub cloud1 or sub cloud2, only one local checkpoint is used in this simulator. Local checkpoint contains information like server status(active or deactive), job status(executing, waiting or finished), server name and also remaining time of threads(execution time + waiting time) etc.

• C.    Failure of Nodes and load rebalancing after 4 seconds to successfully implement failover strategy, node A and E set to be failed after 4 seconds.

• 1)    When checkpoint rerun time is 2 : Fig. 10 illustrates the local checkpoint when checkpointing rerun interval is 2.

After 4 seconds CSP will detect that node A and E has failed and it transfer load of node A and E to other lightly loaded active nodes if in checkpoint job status has not been updated with finished. In Fig. 10 it has shown that the threads which were executed successfully on node A and E before failure and checkpoint has updated their state as finished, need not to be rerun after failure of node A and E after 4 seconds.

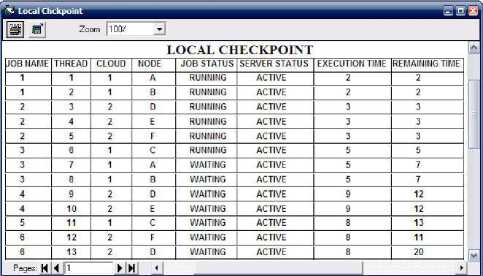
Fig. 9. Local checkpoint

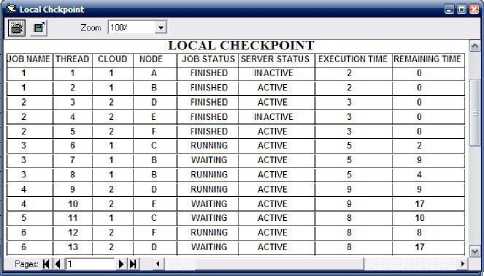
Fig. 10. Local checkpoint with interval 2

• 2)    When checkpoint rerun time is 5 : Fig. 11 illustrates the local checkpoint when checkpointing rerun interval is 5. It can be seen in Fig. 11 that as failure occur before checkpoint rerun, so it is required to re-execute the threads which were executed on failed node successfully. So it is required to transfer load of node A and E to other lightly loaded active nodes.

• 3)    When checkpoint rerun time is 10 : Fig. 12 illustrates the local checkpoint when checkpointing rerun interval is 10. It can be seen in Fig. 12 that as failure occur before checkpoint rerun, so it is required to reexecute the threads which were executed on failed node successfully. So it is required to transfer load of node A and E to other lightly loaded active nodes.

• D.    Failure of Nodes and load rebalancing after 8 seconds to successfully compare checkpoint interval variations, node A and E set to be failed after 4 seconds.

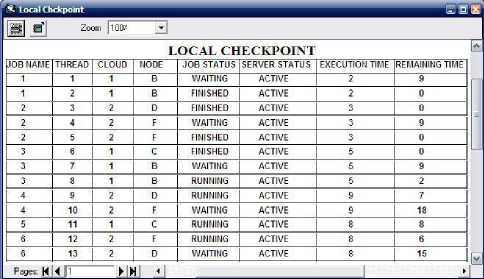
Fig. 11. Local checkpoint with interval 5

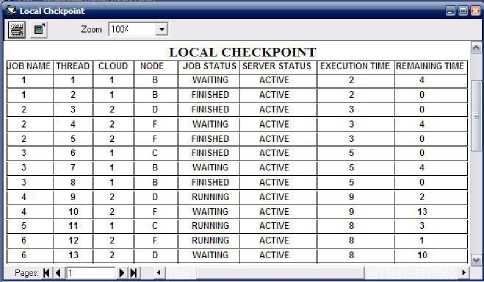
Fig. 12. Local checkpoint with interval 10

• 1)    When checkpoint rerun time is 2 : Fig. 13 illustrates the local checkpoint when checkpointing rerun interval is 2. After 4 seconds CSP will detect that node A and E has failed and it transfer load of node A and E to other lightly loaded active nodes if in checkpoint job status has not been updated with finished. In Fig. 13 it has shown that the thread which was executed successfully on node A and E before failure and checkpoint has updated their state as finished, need not to be rerun after failure of node A and E after 4 seconds.

• 2)    When checkpoint rerun time is 5 : Fig. 14 illustrates the local checkpoint when checkpointing rerun interval is 5. After 8 seconds CSP will detect that node A and E has failed and it transfer load of node A and E to other lightly loaded active nodes if in checkpoint job status has not updated with finished. In Fig. 14 it has shown that the threads which were executed successfully on node A and E before failure and checkpoint has updated their state as finished, need not to be rerun after failure of node A and E after 4 seconds.

• 3)    When checkpoint rerun time is 10 : Fig. 15 illustrates the local checkpoint when checkpointing rerun interval is 10. It can be seen in Fig. 15 that as failure occur before checkpoint rerun, so it is required to reexecute the threads which were

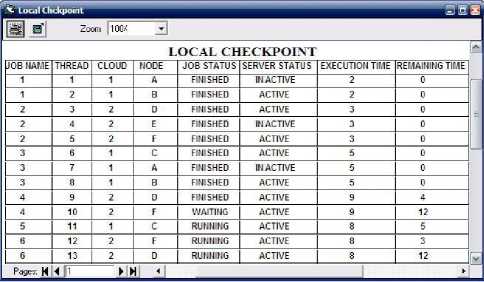
Fig. 13. Local checkpoint with interval 2

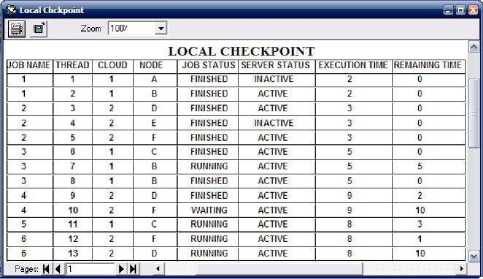
Fig. 14. Local checkpoint with interval 5

executed on failed node successfully. So it is required to transfer load of node A and E to other lightly loaded active nodes.

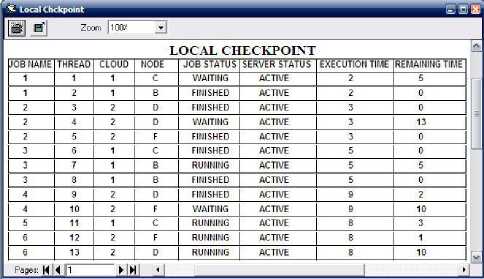
Fig. 15. Local checkpoint with interval 10

• IX.    PERFORMANCE ANALYSIS

In order to do performance analysis, comparisons table has been made. This section give the performance comparison of different rerun intervals using different performance metrics, then performance charts are given which will allow CSP to decide which rerun time is better. For better comparison it has been assumed that checkpoint overhead cost(C) = 1 and also job migration cost(R)= 1.

• A.    When failure of nodes occur after 4 seconds

Table II and III is showing the comparison of different checkpointing intervals (rerun time) using suitable metrics, when failure of nodes occur after 4 seconds.

Interval	TET	AET	TWT	AWT
2 sec’s	121	9.30	51	3.92
5 sec’s	141	10.84	71	5.46
10 sec’s	139	10.70	69	5.31

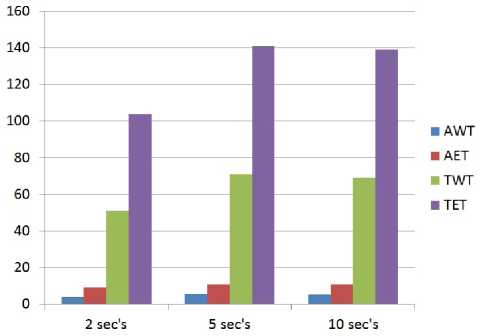
Fig. 16. Graphical representation of Table II

Fig. 16 is showing the results graphically using the data that has shown in Table III. It is clearly showing that when checkpointing interval is 2 seconds the it will give better results than other intervals but it has highest checkpointing overhead cost.

TABLE IV. COMPARISON OF DIFFERENT CHECKPOINTING INTERVALS

Metric/Interval=	2 sec’s	5 sec’s	10 sec’s
MaxWT	13	14	14
MaxET	21	23	23
No. of Thr. restar.	2	4	4
Chp. Ovs. (20 sec’s)	10	4	2
Thp(10 sec’s)	7	5	5
Waiting Thr.	6	8	8
Chp. Ratio	1.6	1.4	1.3

Fig. 17 is showing the graphical results using the data that has shown in Table III. It is clearly shown that using Table III and Fig. 17 that when checkpointing interval= 2 seconds then purposed algorithm will give better results than other intervals but it has highest checkpointing overhead cost.

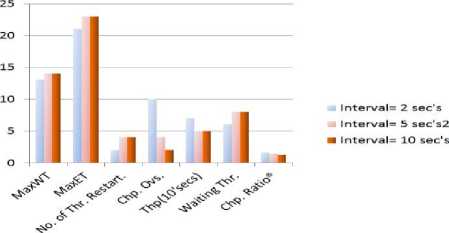
Fig. 17. Graphical representation of Table III

• B.    When failure of nodes occur after 8 seconds

Table IV is showing the comparison of different checkpointing intervals (rerun time) using suitable metrics, when failure of nodes occur after 8 seconds.

TABLE V. COMPARISON BASED ON EXECUTION AND WATITING TIME

Interval	TET	AET	TWT	AWT
2 sec’s	104	8	34	2.61
5 sec’s	114	8.77	44	3.38
10 sec’s	147	11.31	77	5.92

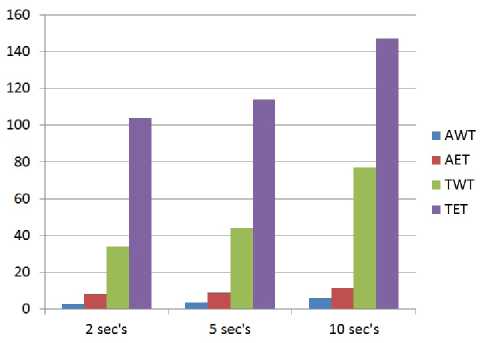
Fig. 18. Graphical representation of Table IV

Fig. 18 is showing the graphical results using the data that has shown in Table IV. It is clearly shown that using Table IV and Fig. 18 that when checkpointing interval= 2 seconds then purposed algorithm will give better results than other intervals but it has highest checkpointing overhead cost, however when interval is 5 it give optimal results as shown in Fig. 18.

TABLE VI. COMPARISON OF DIFFERENT CHECKPOINTING INTERVALS

Metric/Interval=	2 sec’s	5 sec’s	10 sec’s
MaxWT	12	12	20
MaxET	20	20	23
No. of Thr. restar.	1	2	4
Chp. Ovs. (20 sec’s)	10	4	2
Thp(10 sec’s)	8	7	5
Waiting Thr.	5	6	8
Chp. Ratio	1.55	1.3	1.3

Fig. 19 is showing the graphical results using the data that has shown in Table V. It is clearly shown that using Table V and Fig. 19 that when checkpointing interval= 2 seconds then purposed algorithm will give better results than other intervals but it has highest checkpointing overhead cost, however when interval is 5 it give optimal results as shown in Fig. 19. Therefore it is better to set interval = 5 seconds corresponding to the data shown in Table IV and V.

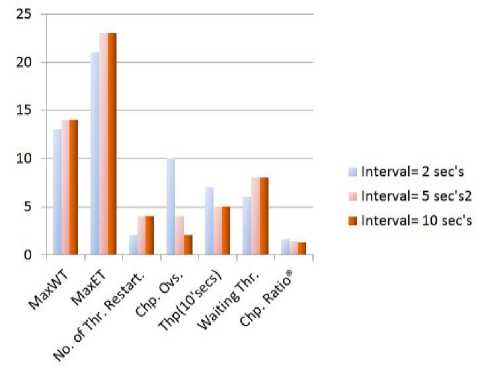
Fig. 19. Graphical representation of Table V

• X.    CONCLUSION AND FUTURE DIRECTIONS

This paper has proposed a novel technique to analyse the performance of checkpointing algorithms. The offered technique is based on failover algorithms which will provide high availability to the clouds clients, and estimating the required measures by varying the interval time of integrated checkpoint algorithms. A suitable cloud environment is made with 6 service nodes to analyse the execution time of the parallel jobs and also integrated checkpointing algorithms will control the overall execution of the jobs and also provide high availability in case of node failure.

Comparisons have been made in this research work by taking different failure time of nodes and checkpointing intervals. Comparisons are made using different well known parameters and metrics. It has been proved that setting of the checkpointing interval is a critical task as if checkpoint rerun time has been decrease too much then it adds too many overheads in the execution time of jobs and if checkpoint rerun time has been increased too much then it will not give good results.

The proposed technique is not limited to the scenario and number of nodes described in this paper, or to the failure of nodes used in this research work. It can be used to analyse any checkpointing high availability scheme, with various scenarios. The proposed technique can be also used to provide analytical answers to problems that haven’t been dealt with before or were handled by a simulation study. Examples of such problems are deriving the number of checkpoints that minimizes the average completion time and computing the probability of meeting a given deadline.

• XI.    FUTURE DIRECTIONS

In the near future, this research will be extending to the multilevel checkpointing integration for the case where the multilevel checkpointing interval is not fixed. By using the interval where rerun time depend upon the nature of the executing jobs expecting that the extended technique will give less waste time than the proposed one. In addition, this research will be extended for improving the way to save and rerun checkpointing. For example, in some requests, there are many communications between nodes. If one performs a checkpoint while there is a large amount of communications going on, the checkpointing overhead will become more expensive. Therefore, the communication or I/O transfer rate may be another factor to consider when performing a checkpoint. In this paper homogeneous nodes has been considered for simulation environment, in future work heterogeneous nodes will be used for better results.